归并排序 图解 递归 + 非递归 + 笔记
前置知识:讲解019-算法笔试中处理输入和输出,讲解020-递归和master公式
- (1)左部分排好序,右部分排好序,利用merge过程让左右整体有序
- (2)merge过程:谁小拷贝谁,直到左右两部分所有的数字耗尽
- (3)递归实现和非递归实现
- (4)时间复杂度O(n*logn)
- (5)需要辅助数组,所以额外空间复杂度O(n)
- (6)归并排序为什么比O(n^2)的排序快?因为比较行为没有浪费!
- (7)利用归并排序的便利性可以解决很多问题,例如归并分治
注意:有些资料说可以用原地归并排序,把额外空间复杂度变成O(1),不要浪费时间去学。因为原地归并排序确实可以省空间,但是会把复杂度变成O(n^2)
- 对这个数组arr=[6,4,2,3,9,4] ,进行归并排序


- 挑其中一步来演示: 把[2,4,6]和[3,4,9]合并(merge)
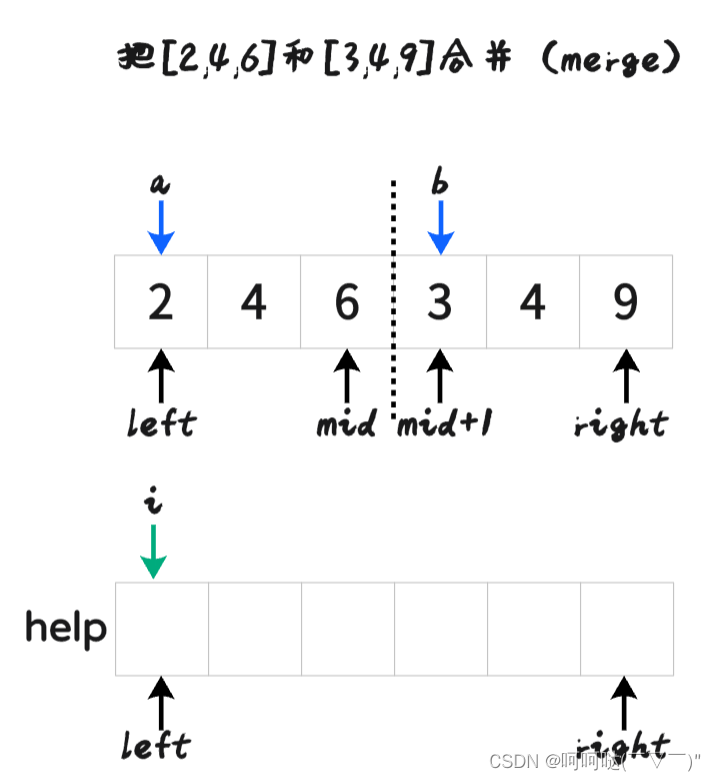



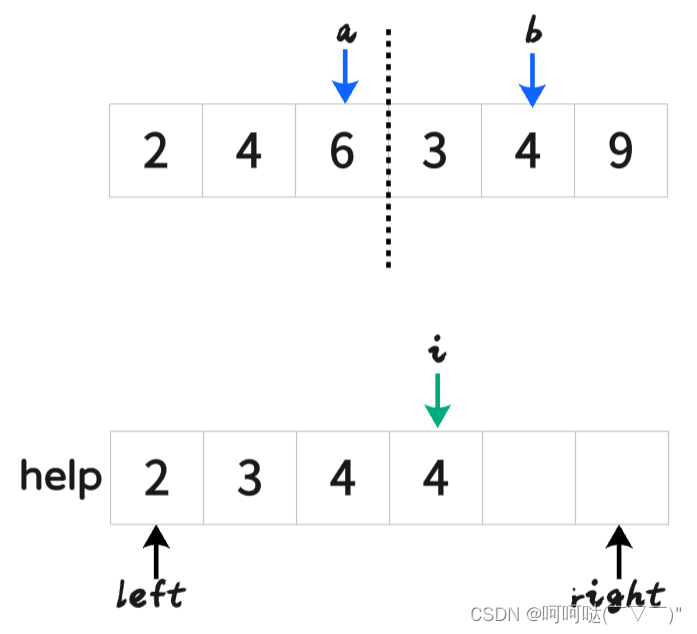
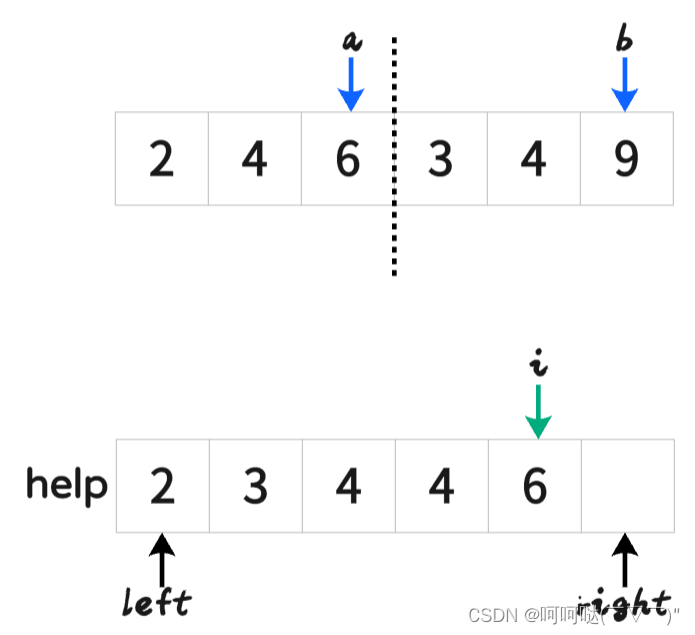
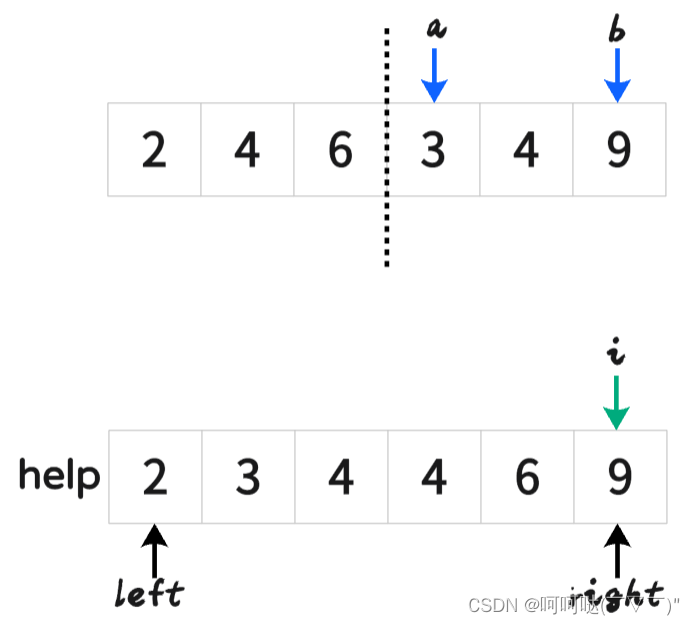

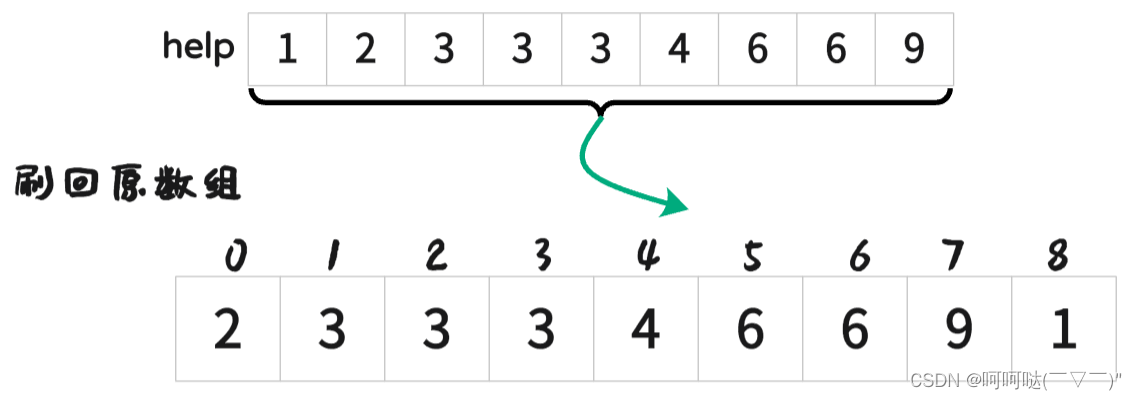
最后再刷回原数组

void merge(vector<int>& arr,int left, int mid, int right) {int n = right - left + 1;vector<int> help(n,0);int i = 0;int a = left;int b = mid + 1;while (a <= mid && b <= right) {help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];}// 左侧指针,右侧指针,必有一个越界,另一个不越界while (a <= mid) {help[i++] = arr[a++];}while (b <= right) {help[i++] = arr[b++];}for (i = 0; i <n; i++) { // 把 help 里面的数据重新刷回到原数组arrarr[i+left] = help[i];}
}(1)归并排序递归版
// 递归方法
void mergeSort(vector<int>& arr, int left, int right) {if (left == right) return;int mid = (left + right) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);
}(2)归并排序非递归版

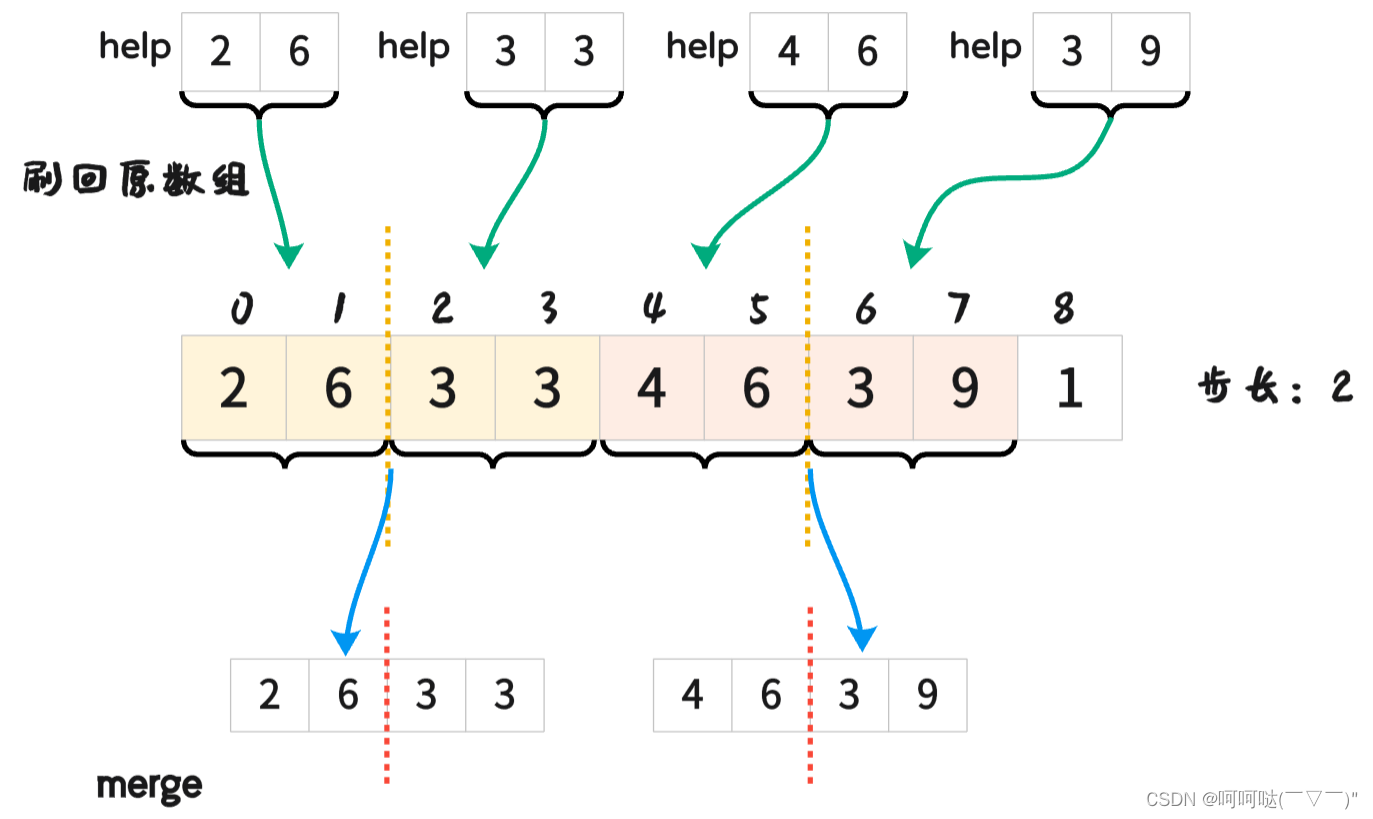


// 归并排序非递归版
// 时间复杂度:O(n * logn)
// 空间复杂度:O(n)
void mergeSort2(vector<int>& arr) {int n = arr.size();// 一共发生O(logn)次for (int left, mid, right, step = 1; step < n; step <<= 1) {// 内部分组merge,时间复杂度:O(n)left = 0;while (left < n) {mid = left + step - 1;if (mid + 1 >= n) {// 已经没有右侧了break;}// 有右侧,求右侧的右边界right = min(left + (step << 1) - 1, n - 1);// left ... mid mid+1 ... right// left ... mid mid+1 ... right// left ... mid mid+1 ... rightmerge(arr,left, mid, right);left = right + 1;}}
}完整代码:
#include <iostream>
#include <vector>
using namespace std;void merge(vector<int>& arr,int left, int mid, int right) {int n = right - left + 1;vector<int> help(n,0);int i = 0;int a = left;int b = mid + 1;while (a <= mid && b <= right) {help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];}// 左侧指针,右侧指针,必有一个越界,另一个不越界while (a <= mid) {help[i++] = arr[a++];}while (b <= right) {help[i++] = arr[b++];}for (i = 0; i <n; i++) { // 把 help 里面的数据重新刷回到原数组arrarr[i+left] = help[i];}
}/*归并排序递归版假设left...right一共 n 个数T(n) = 2 * T(n/2) + O(n)a = 2,b = 2,c = 1根据master公式,时间复杂度:O(n * logn)空间复杂度:O(n)
*/
// 递归方法
void mergeSort(vector<int>& arr, int left, int right) {if (left == right) return;int mid = (left + right) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);
}// 归并排序非递归版
// 时间复杂度:O(n * logn)
// 空间复杂度:O(n)
void mergeSort2(vector<int>& arr) {int n = arr.size();// 一共发生O(logn)次for (int left, mid, right, step = 1; step < n; step <<= 1) {// 内部分组merge,时间复杂度:O(n)left = 0;while (left < n) {mid = left + step - 1;if (mid + 1 >= n) {// 已经没有右侧了break;}// 有右侧,求右侧的右边界right = min(left + (step << 1) - 1, n - 1);// left ... mid mid+1 ... right// left ... mid mid+1 ... right// left ... mid mid+1 ... rightmerge(arr,left, mid, right);left = right + 1;}}
}int main() {vector<int> arr = { 6,4,2,3,9,4};int n = arr.size();mergeSort(arr, 0, n - 1);//mergeSort2(arr);for (int i = 0; i < n; i++) {cout << " " << arr[i] << " " << endl;}system("pause");return 0;
}完整图:

参考和推荐视频:
算法讲解021【必备】归并排序_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1wu411p7r7/?spm_id_from=333.999.list.card_archive.click&vd_source=a934d7fc6f47698a29dac90a922ba5a3
https://www.bilibili.com/video/BV1wu411p7r7/?spm_id_from=333.999.list.card_archive.click&vd_source=a934d7fc6f47698a29dac90a922ba5a3
相关文章:
归并排序 图解 递归 + 非递归 + 笔记
前置知识:讲解019-算法笔试中处理输入和输出,讲解020-递归和master公式 (1)左部分排好序,右部分排好序,利用merge过程让左右整体有序(2)merge过程:谁小拷贝谁,直到左右两部分所有的数字耗尽(3)递归实现和非递归实现(4…...
2023 年最好的 Android 系统修复/刷机应用程序和软件
任何 Android 设备要顺利运行,其操作系统必须运行良好。幸运的是,对于大多数 Android 用户来说,这是不间断的。设备运行良好,打电话、共享文档等都没有问题。尽管如此,Android 操作系统可能会停止运行。这可能是由于特…...

Linux下内网穿透实现云原生观测分析工具的远程访问
📑前言 本文主要是Linux下内网穿透实现云原生观测分析工具的远程访问设置的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 &…...

卡数据兼容性要求-M2M架构
EUM 应在生产 eUICC 过程中安装并初始化 ISD-R. eUICC 出厂后, ISD-R 应进入 GlobalPlatform Card Specification [GP CS]第 5.3 节中定义的生命周期状态 "PERSONALIZED". ISD-R 权力授予应遵循[GS RPT]附录 C 中的定义. EUM 应在 eUICC 生产过程中安装并…...
C++入门篇3(类和对象【重点】)
文章目录 C入门篇3(类和对象【重点】)1、面向过程和面向对象2、类的引入3、类的定义4、类的访问限定符及封装4.1、访问限定符4.2、封装 5、类的作用域6、类的实例化(对象)7、类对象模型7.1、类对象的存储方式7.2、结构体ÿ…...
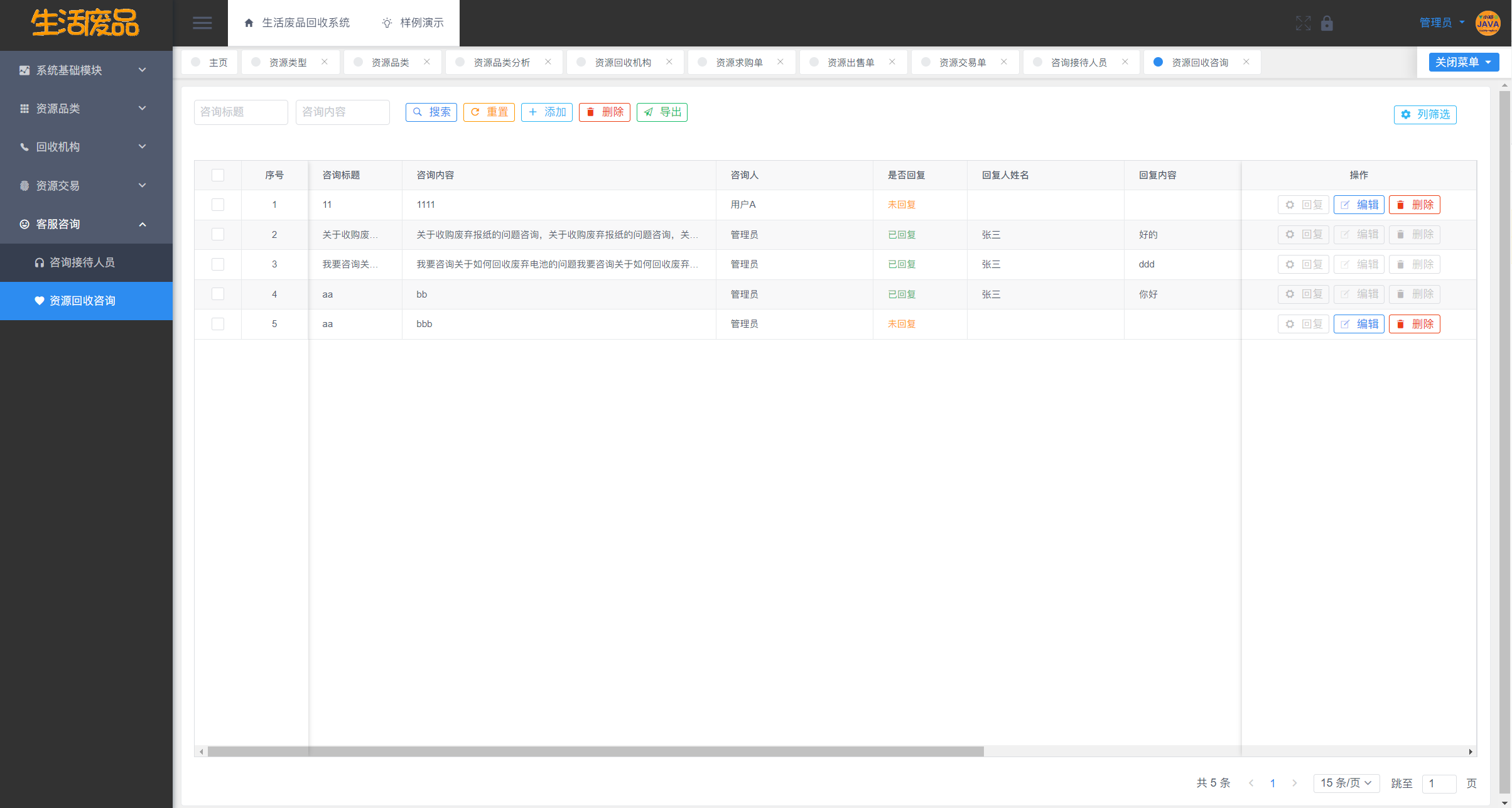
【开源】基于Vue.js的生活废品回收系统的设计和实现
目录 一、摘要1.1 项目介绍1.2 项目详细录屏 二、研究内容三、界面展示3.1 登录注册3.2 资源类型&资源品类模块3.3 回收机构模块3.4 资源求购/出售/交易单模块3.5 客服咨询模块 四、免责说明 一、摘要 1.1 项目介绍 生活废品回收系统是可持续发展的解决方案,旨…...
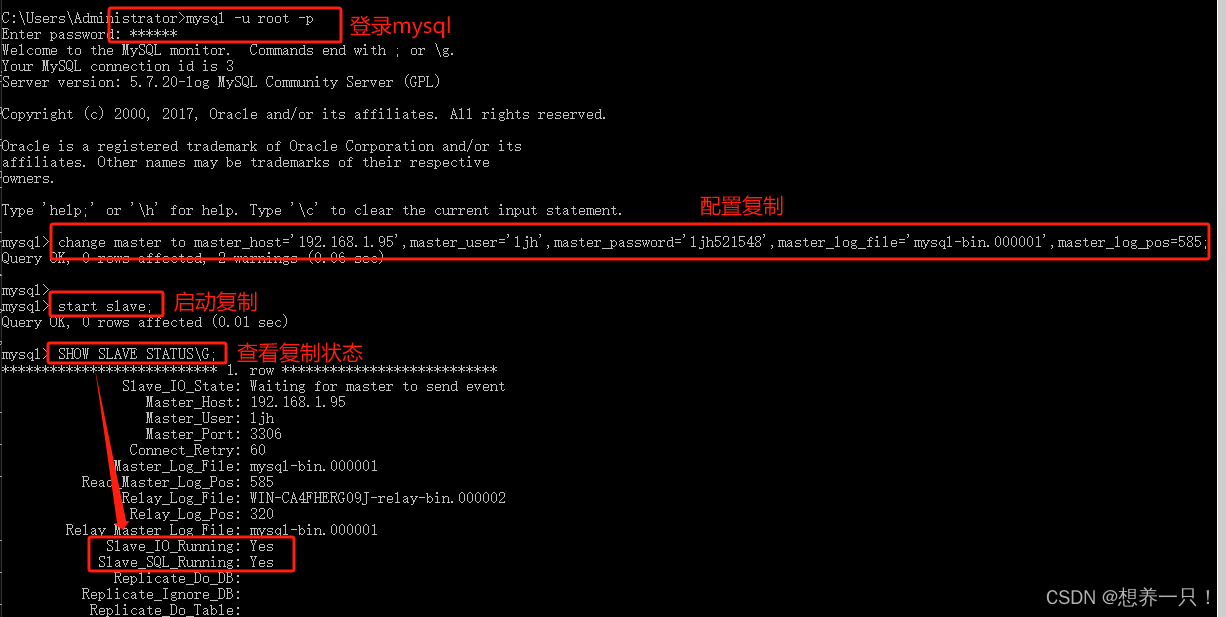
Mysql配置主从复制-GTID模式
目录 主从复制 主从复制的定义 主从复制的原理 主从复制的优势 主从复制的形式 主从复制的模式 主从复制的类型 GTID模式 GTID的概念 GTID的优势 GTID的原理 GTID的配置 Mysql主服务器 编辑 Mysql从服务器 编辑 主从复制 主从复制的定义 是指把数据从一个…...

Flink之状态管理
Flink状态管理 状态概述状态分类 键控、按键分区状态概述值状态 ValueState列表状态 ListStateMap状态 MapState归约状态 ReducingState聚合状态 Aggregating State 算子状态概述列表状态 ListState联合列表状态 UnionListState广播状态 Broadcast State 状态有效期 (TTL)概述S…...

[Mac软件]Adobe Media Encoder 2024 V24.0.2免激活版
软件说明 使用Media Encoder,您将能够处理和管理多媒体。插入、转码、创建代理版本,并几乎以任何可用的格式输出。在应用程序中以单一方式使用多媒体,包括Premiere Pro、After Effects和Audition。 紧密整合 与Adobe Premiere Pro、After …...
Bytebase 2.11.0 - 支持 OceanBase Oracle 模式
🚀 新功能 支持 OceanBase Oracle 模式。支持设置 MySQL 在线变更参数。新增项目数据库查看者的角色。 🎄 改进 支持在项目中直接选择所有用户并为之添加角色。 调整了项目页面的布局。在 SQL 编辑器中通过悬浮面板展示表和列的详情。 🪦 …...

『CV学习笔记』文本识别算法CRNNSVTR介绍
文本识别算法CRNN&SVTR介绍 文章目录 一. 文本识别1.1. 文本识别方法介绍1.1.1. 规则文本识别1.1.2. 不规则文本识别1.2. CRNN算法原理1.2.1. CRNN基本网络结构1.3. SVTR算法原理二. 参考文献一. 文本识别 文本识别是OCR(Optical Character Recognition)的一个子任务,其…...

HaaS510开板式DTU真机连云:上报监测数据至阿里云物联网平台
背景 HaaS: Hardware as a Service。 HAAS510 是一种开板式 DTU ,旨在为用户已开发好的设备快速增加 4G 连云能力的 4G CAT1 数传模块。它通过将模组与用户设备集成到一个外壳内,既保持设备的一体性,又降低重新开发 PCB 的时间消耗和模组开…...

贾扬清开源 AI 框架 Caffe | 开源英雄
【编者按】在开源与人工智能的灿烂星河里,贾扬清的名字都格外地耀眼。因为导师 Trevor Darrell 教授的一句“你是想多花时间写一篇大家估计不是很在意的毕业论文,还是写一个将来大家都会用的框架?”,学生贾扬清一头扎进了创 Caffe…...

【objectarx.net】使用公式自动更新表格项的内容
使用公式自动更新表格项的内容...

CSS 移动端 1px(线条/边框) 不同机型上显示粗细不同,解决办法
由于不同的手机有不同的像素密度导致的。如果移动显示屏的分辨率始终是普通屏幕的2倍,1px的边框在devicePixelRatio2的移动显示屏下会显示成2px,所以在高清瓶下看着1px总是感觉变胖了 <!DOCTYPE html> <html lang"en"> <head&g…...
)
vue3使用vuex的示例(模块化功能)
目录 1. store/index.ts 2. main.ts 3. App.vue调用 4. 如果删除moduleA的namespaced属性, 保留moduleB的namespaced:true 5. 则App.vue修改为: 1. store/index.ts 注意: 需要使用时带上模块名称的namespaced必须为true, 不写或者为false时调用时不需要写模块名称(获取st…...

Vatee万腾的科技决策力奇迹:Vatee科技决策力的独特之选
在金融投资的复杂领域中,Vatee万腾以其独特的科技决策力创造了一场真正的奇迹。这不仅是一种引领投资者走向成功的选择,更是一种开启新时代的科技决策奇迹。 Vatee的科技决策力背后蕴藏着强大的智慧和创新。通过大数据分析、智能算法的运用,V…...

ai技术是怎么换脸的,实现原理是什么,有那些软件
人工智能(AI)在近年来的迅猛发展中,带来了许多令人惊叹的技术创新,其中之一就是人工智能换脸技术。这项技术通过深度学习和图像处理的手段,使得用户可以将自己的面孔替换成其他人物,引发了广泛的讨论和应用…...
在IDEA中使用maven项目总结
一 什么是maven Maven本身也是Java写的,他是一款服务于Java平台的自动化构建工具 Maven是一个项目管理工具,旨在简化软件项目的构建、依赖管理和项目信息管理。它使用基于项目对象模型(Project Object Model,POM)的…...

oracle备份一个表需要做的操作
在 Oracle 中备份一个表可以通过以下步骤完成,包括备份表结构(DDL)和备份表数据(DML): 备份表结构(DDL): 使用 CREATE TABLE AS SELECT: 创建一个新表&#…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
