常见排序算法之快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
基本思想为∶任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return; int div = partion(array, left, right);QuickSort(array, left, div); QuickSort(array, div+1, right);
}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,我们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有:
1.hoare版本
2.挖坑法
3.前后指针版本
下面将介绍三种方法,在此之前我们现需写一个三数取中代码:
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) {return left;}else{return right;}}else {if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) {return left;}else{return right;}}
}一、hoare版本
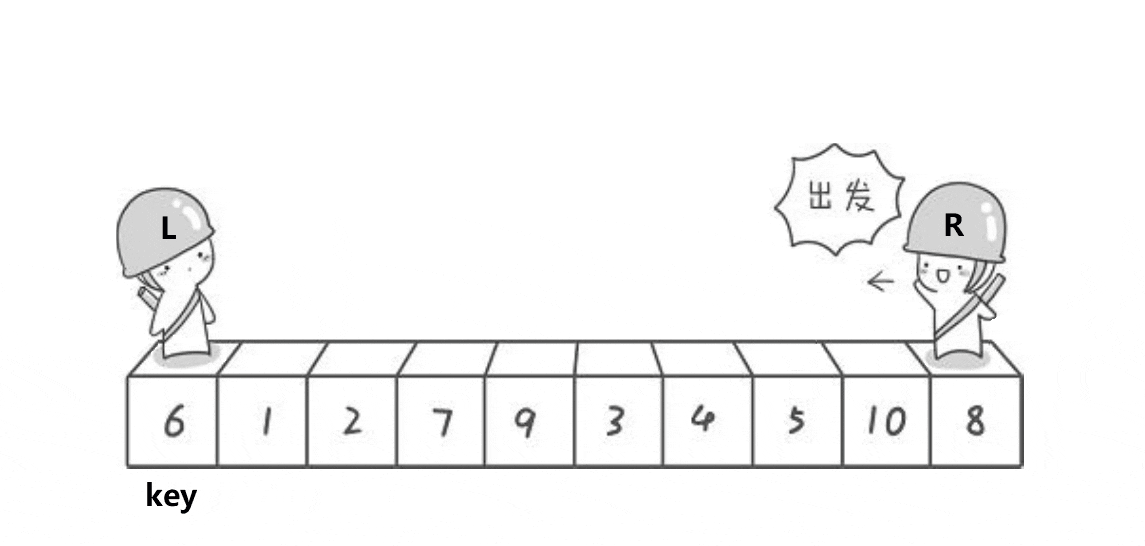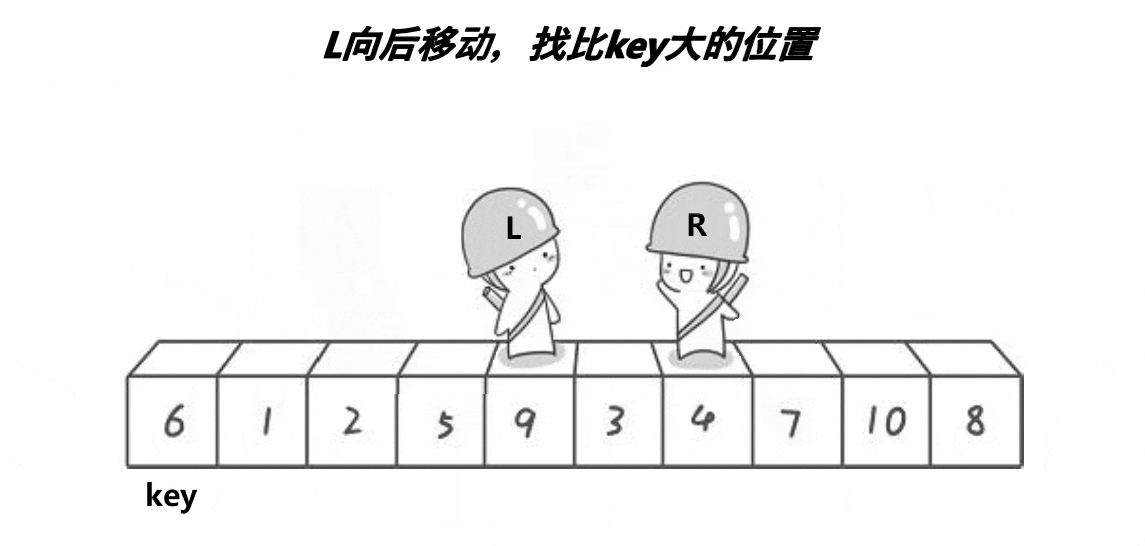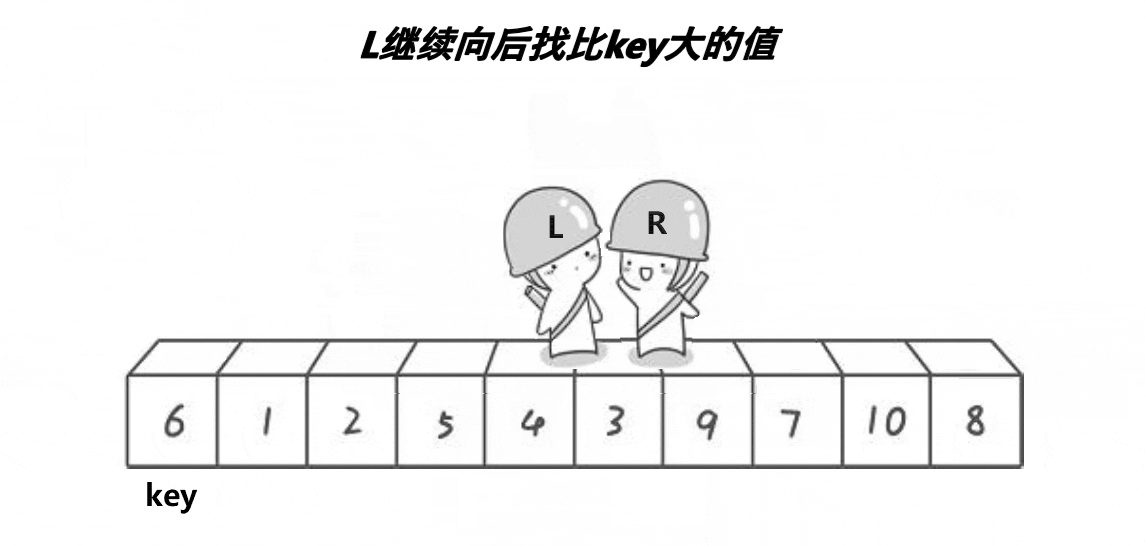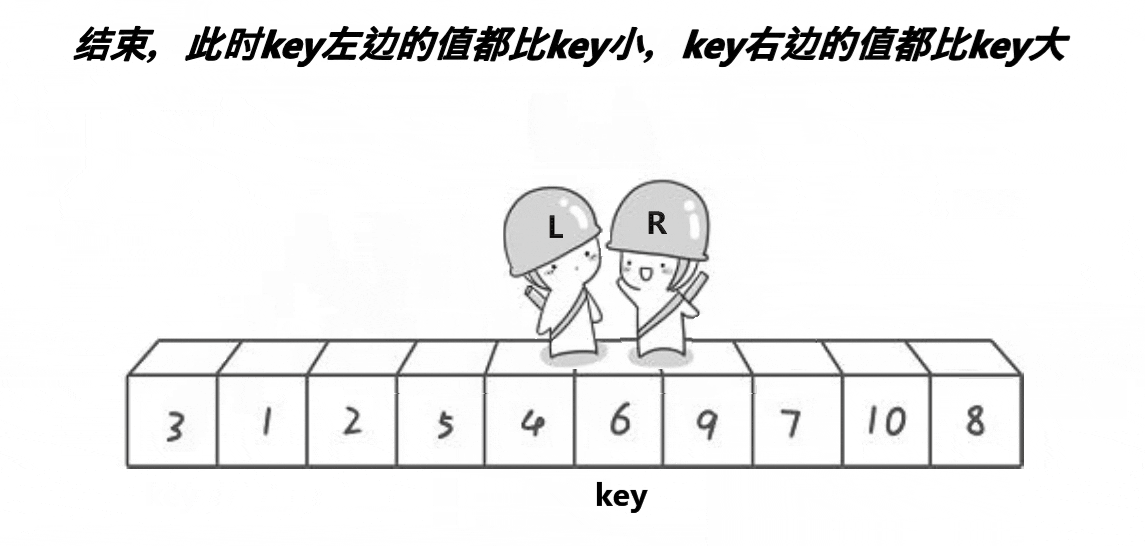
具体步骤
- 先选取数组左边的第一个数作为key,定义一个左下标left指向最左边的数,定义一个右下标right指向最右边的数。
- 然后让right先往左遍历,找到第一个比key大的值,让left后向右遍历,找到第一个比key小的值。
- 这时,左边的值都比key小,右边的值都比key大,交换left和right指向的值。
- 这样一趟排序就结束了,key就在了它应该在的位置上。重复以上步骤,直到整个序列有序。
核心代码
int PartSort1(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort1(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void TestQuickSort()
{int a[] = { 6,1,2,7,9,3,4,5,10,8 };QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestQuickSort();return 0;
}实验结果

二、挖坑法
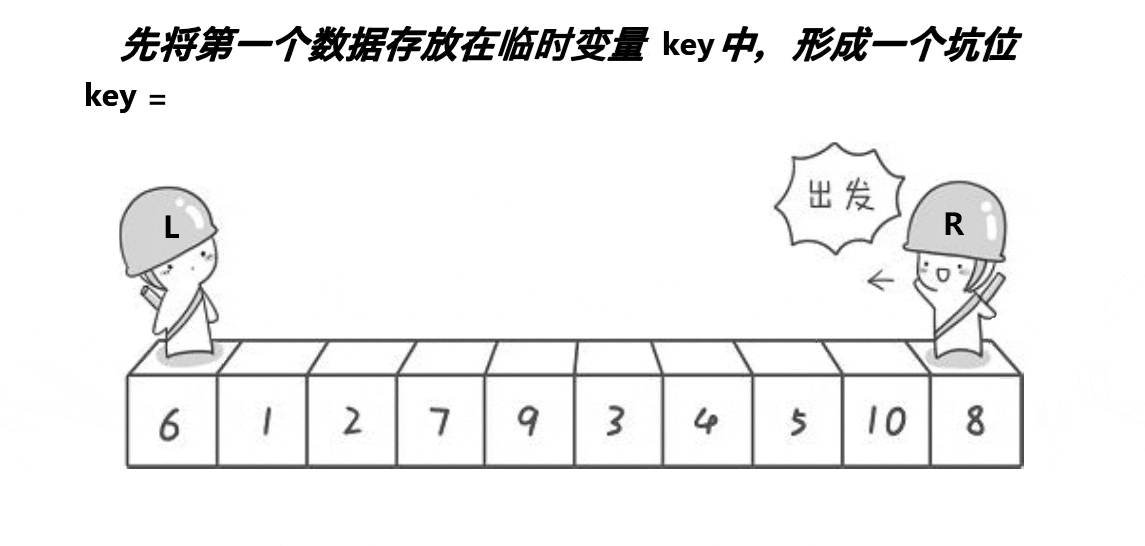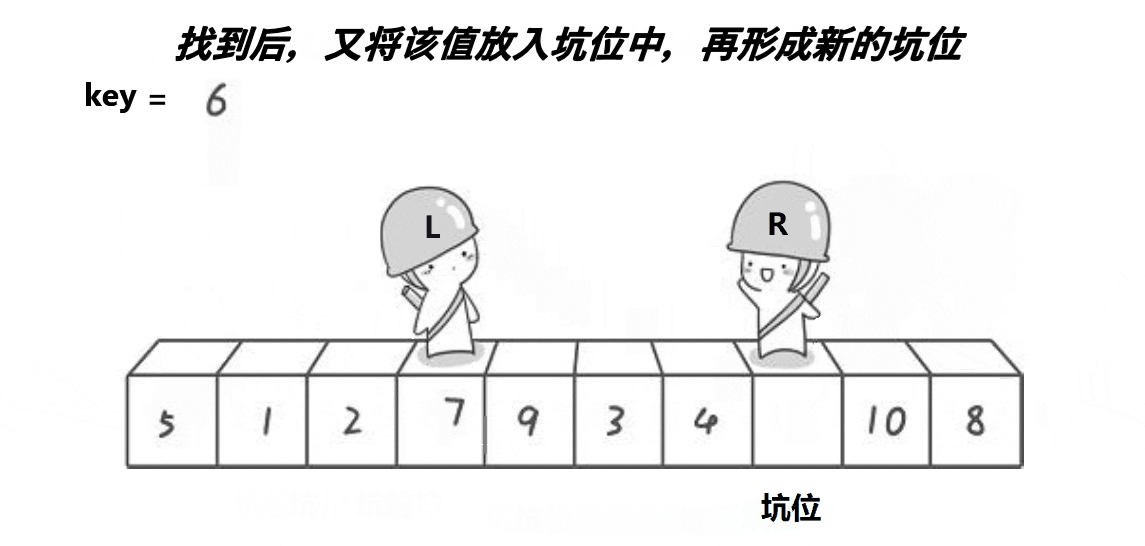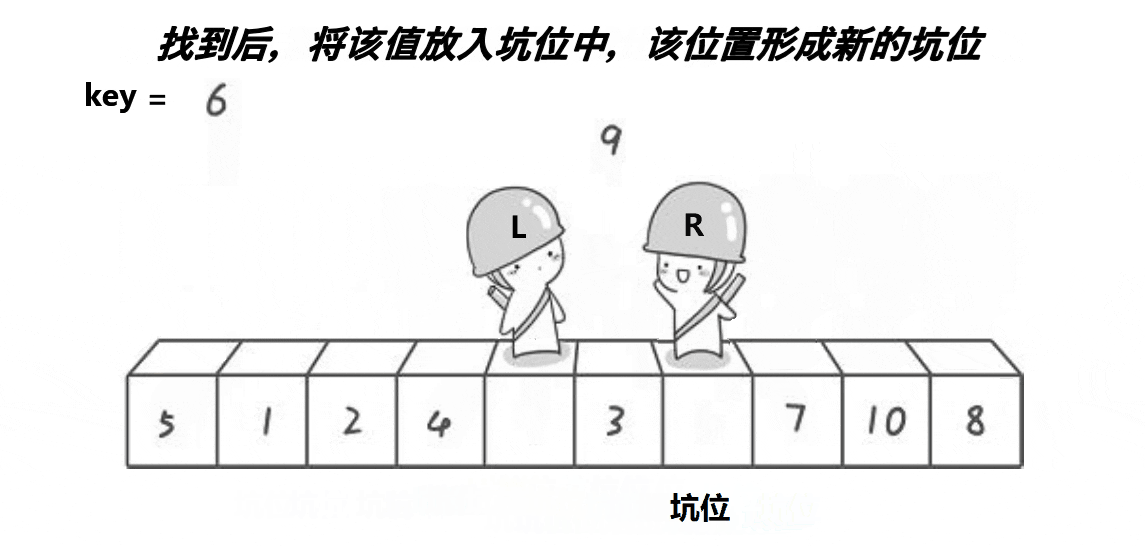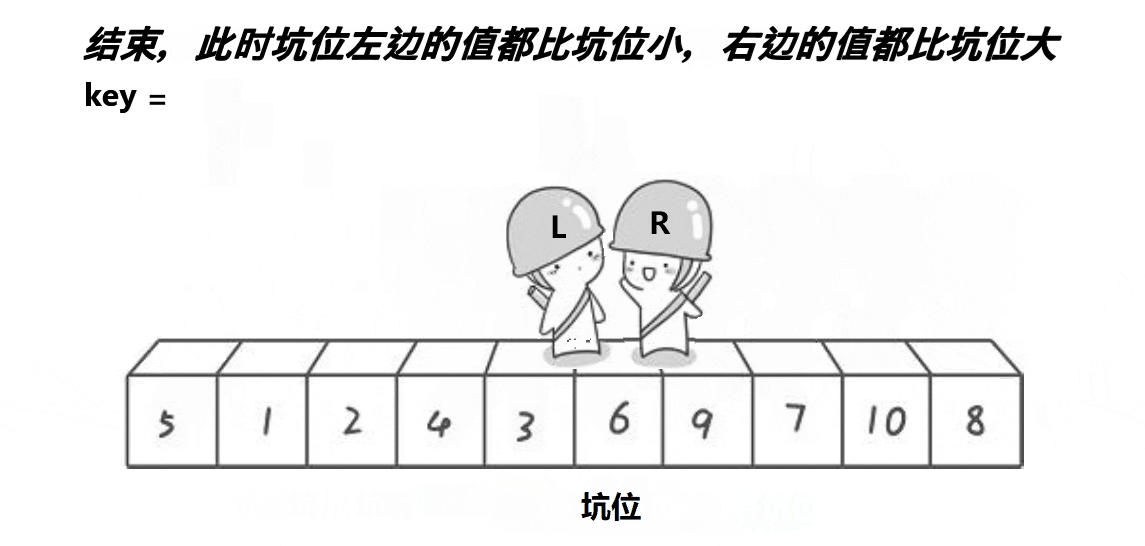
具体步骤
首先设置两个指针,一个指向数组的起始位置,一个指向数组的末尾位置。从末尾位置开始,向前遍历,找到第一个小于基准元素的元素,并将其填入起始位置的坑中。然后从起始位置开始,向后遍历,找到第一个大于基准元素的元素,并将其填入上一步所挖的坑中。重复上述步骤,直到起始位置和末尾位置相遇。此时,将基准元素填入最后一个坑中,这样就完成了一次分区操作。最后对分区后的左右两个子数组,分别递归地进行上述步骤。
核心代码
int PartSort2(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int key = a[left];int hole = left;while (left < right){while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort2(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void TestQuickSort()
{int a[] = { 6,1,2,7,9,3,4,5,10,8 };QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestQuickSort();return 0;
}实验结果

三、前后指针版本
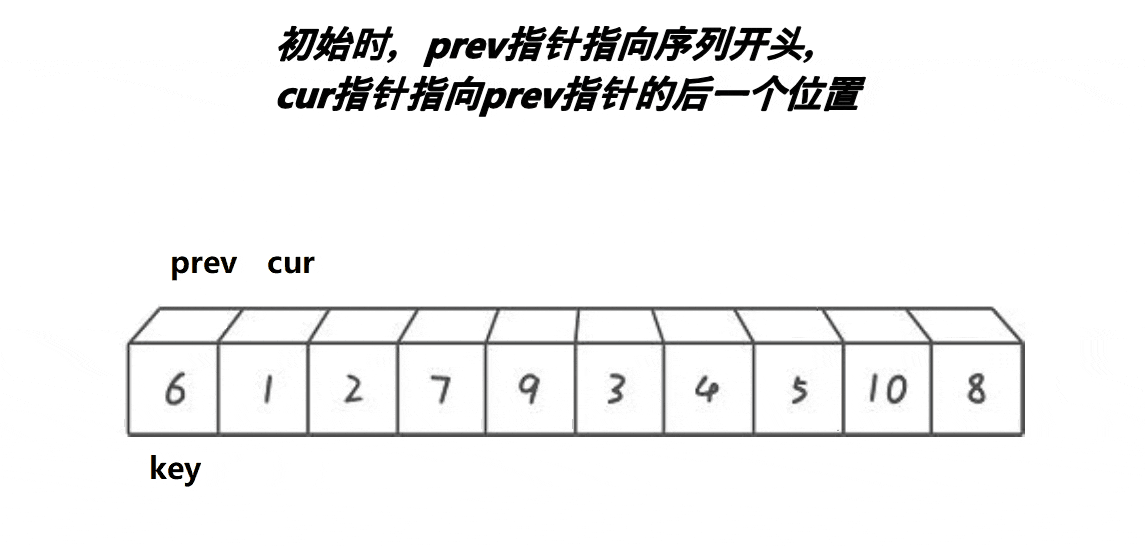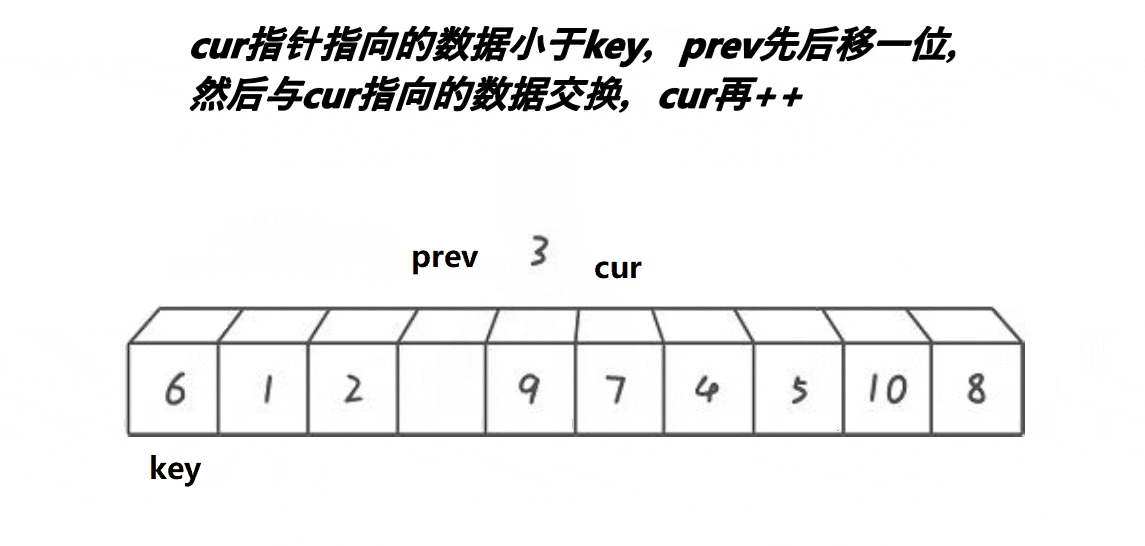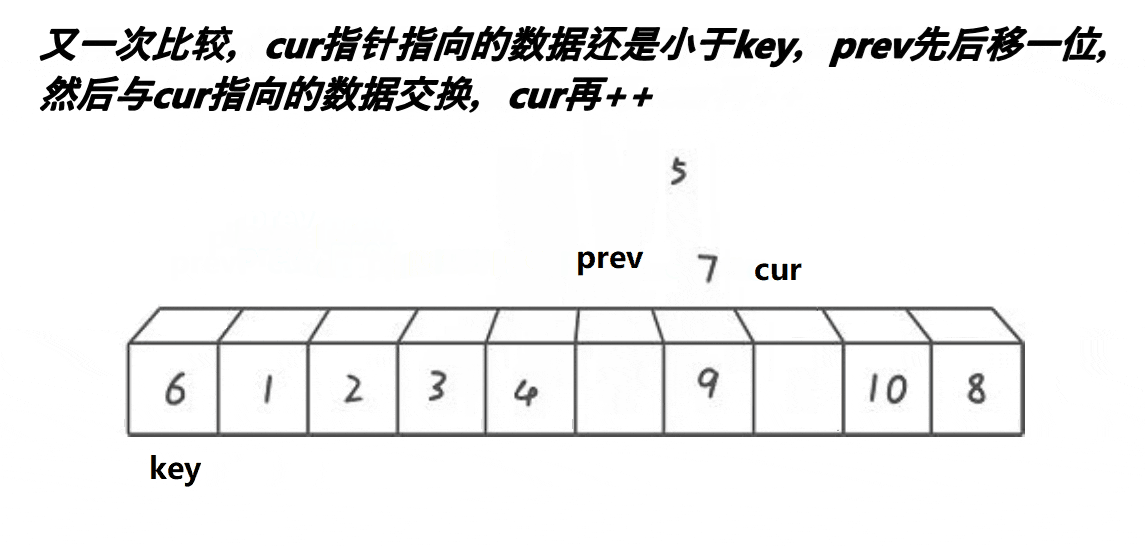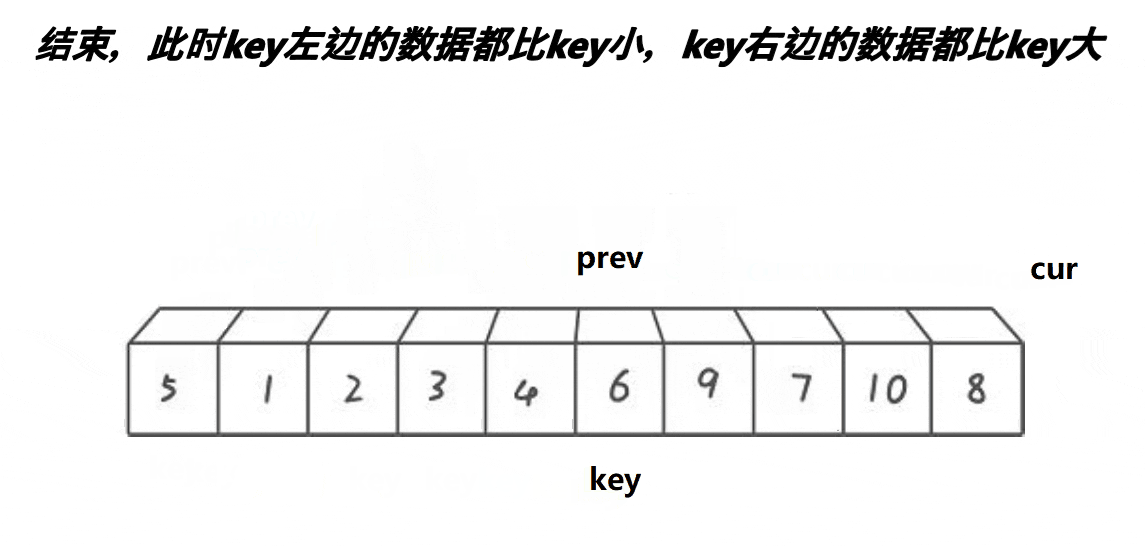
具体步骤
-
选择枢轴元素:在数组中选择一个元素作为枢轴,一般选择第一个元素或最后一个元素。
-
初始化左右指针:左指针指向数组的第一个元素,右指针指向数组的最后一个元素。
-
划分过程:从前往后遍历数组,当找到一个比枢轴大的元素时,将左指针向右移动一位;从后往前遍历数组,当找到一个比枢轴小的元素时,将右指针向左移动一位。当左指针大于等于右指针时,说明已经找到正确的位置,将枢轴与左指针所在位置的元素交换。
-
递归处理:将枢轴左边的部分作为新的子数组,递归调用快速排序函数;将枢轴右边的部分作为新的子数组,递归调用快速排序函数。
核心代码
int PartSort3(int* a, int left, int right)
{int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);return prev;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void TestQuickSort()
{int a[] = { 6,1,2,7,9,3,4,5,10,8 };QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestQuickSort();return 0;
}实验结果

四、非递归版本
快速排序的非递归版本是递归版本的一种优化,主要是通过将递归过程转化为循环来实现。基本思路是将数组分为两部分,一部分比基准值小,另一部分比基准值大,然后对这两部分分别进行快速排序。这个过程可以通过循环来实现,而不是通过递归调用函数自身。
具体步骤
首先从数组中挑选一个元素作为基准值,然后将所有小于基准值的元素移动到基准值的左边,将所有大于基准值的元素移动到基准值的右边。接下来,对基准值左右两边的子数组分别进行相同的操作,直到数组完全有序。
核心代码
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);
}StackDestroy(&s);
}感兴趣的同学可以自行练习。
五、快速排序特性总结
1.快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2.时间复杂度:O(N*logN)
3.空间复杂度:O(logN)
4.稳定性:不稳定
结语:快速排序的相关分享到这里就结束了,希望对大家的学习会有帮助,如果大家有什么问题或者不同的见解,欢迎大家的留言~~~
相关文章:

常见排序算法之快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。 基本思想为∶任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,…...
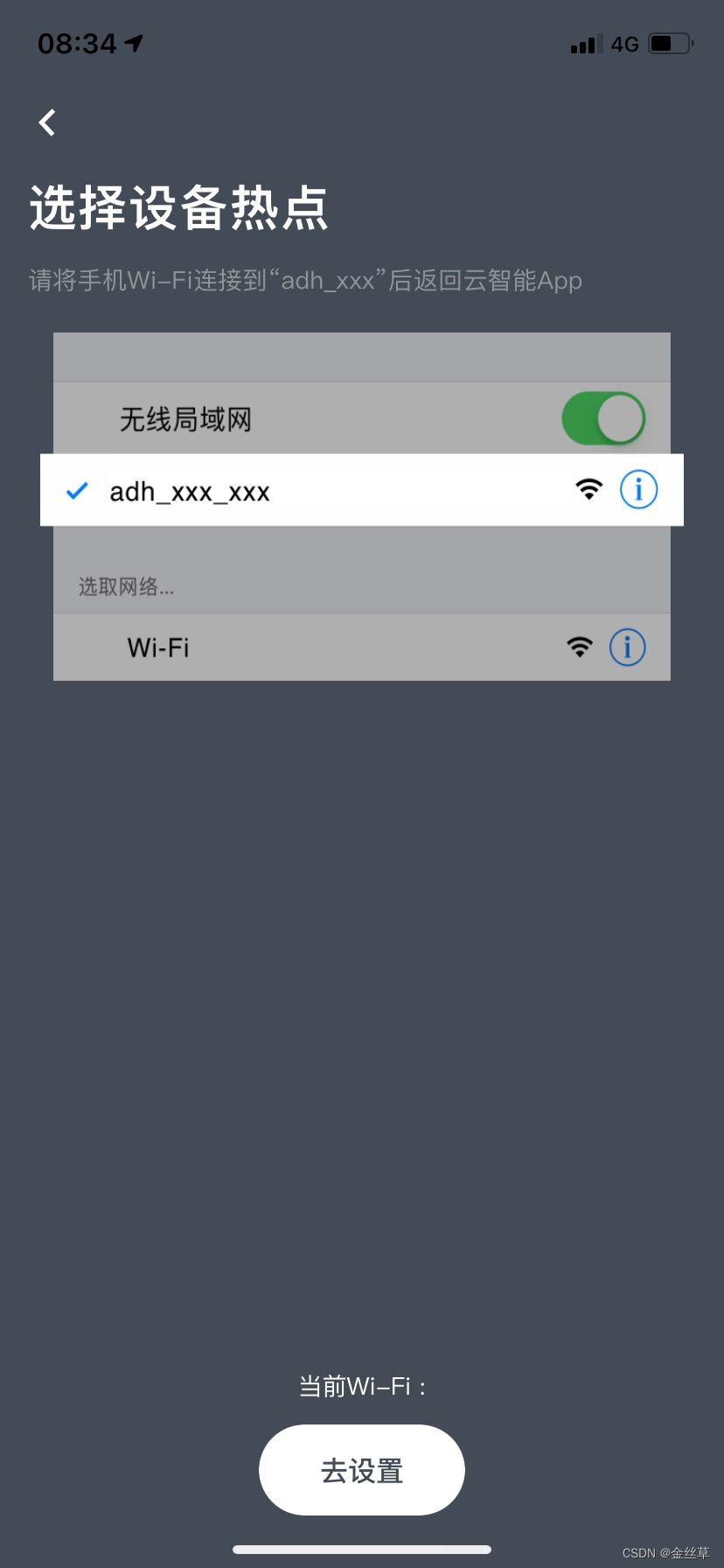
ESP32 C3 smartconfig一键配网报错
AP配网 在调试我的esp32c3的智能配网过程中,发现ap配网使用云智能App是可以正常配置的。 切记用户如果在menu菜单里使能AP配网,默认SSID名字为adh_PK值_MAC后6位。用户可以修改这个apssid的键值,但是要使用云智能app则这个名字的开头必须为ad…...

力扣labuladong——一刷day25
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣528. 按权重随机选择 带权重的随机选择算法 前言 一、力扣528. 按权重随机选择 class Solution {private int[] preSum;private Random rand new Ra…...
从单体到微服务:使用Spring Boot构建事件驱动的Java应用程序
Spring Boot是Pivotal团队设计的一种微服务框架, 基于Spring开发,用于简化新Spring应用的初始搭建及开发过程,提升Spring 开发者的体验。它秉持“约定大于配置”的思想,集成了大量开箱即用的第三方库,支持绝大多数开源…...
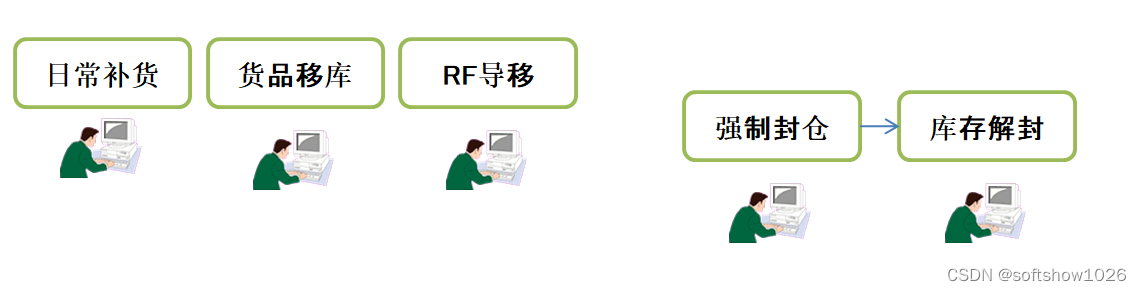
WMS配送中心主要业务流程
业务流程图 入库 波次出库 按门店和门店所属送货路线确定出库波次 入库 出库 移库、封仓 门店欠货能要点 1. 日常补货:分拣仓位商品小于当前商品在该位置的补货下限的时候;生成对此进行补货任务;补货完成后确认任务,系统变更库存…...
)
《LeetCode力扣练习》代码随想录——数组(螺旋矩阵II---Java)
《LeetCode力扣练习》代码随想录——数组(螺旋矩阵II—Java) 刷题思路来源于 代码随想录 59. 螺旋矩阵 II 左闭右开——[x,y) class Solution {public int[][] generateMatrix(int n) {if(n1){return new int[][]{{1}};}int[][] resultnew int[n][n];int…...

计算机毕业设计选题推荐-农产品销售微信小程序/安卓APP-项目实战
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...

Linux AMH 服务器管理面板远程访问
文章目录 1. 前言2. Linux 安装AMH 面板3. 本地访问AMH 面板4. Linux安装Cpolar5. 配置AMH面板公网地址6. 远程访问AMH面板7. 固定AMH面板公网地址8、结语 1. 前言 AMH 是一款基于 Linux 系统的服务器管理面板,它提供了一系列的功能,包括网站管理、FTP …...
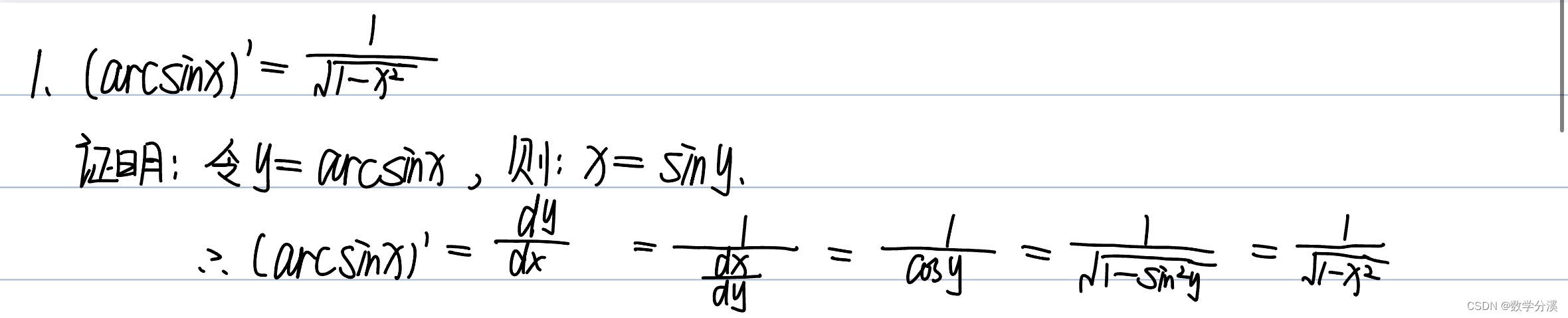
arcsinx的导数
...
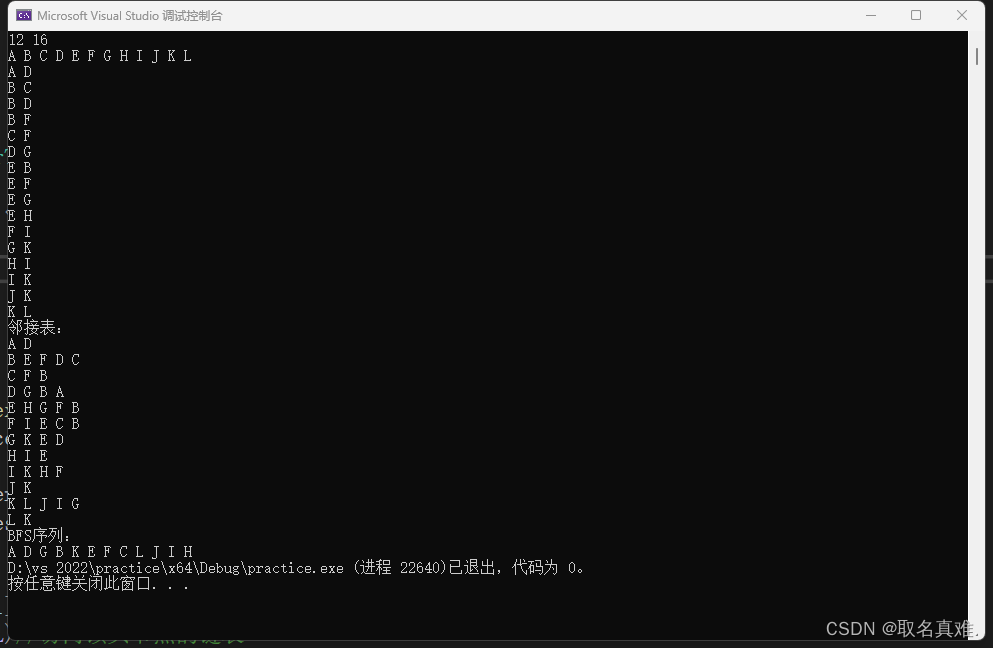
邻接表储存图实现广度优先遍历(C++)
目录 基本要求: 邻接表的结构体: 图的邻接表创建: 图的广度优先遍历(BFS): 邻接表的打印输出: 完整代码: 测试数据: 结果运行: 通过给出的图的顶点和…...

解构赋值详解以及例子
以下是使用解构赋值的所有可能方式的示例代码: 数组解构赋值 const array [1, 2, 3];// 基本形式 const [a, b, c] array; console.log(a); // 1// 只获取部分值 const [, second] array; console.log(second); // 2// 设置默认值 const [d, e, f, g 4] arra…...
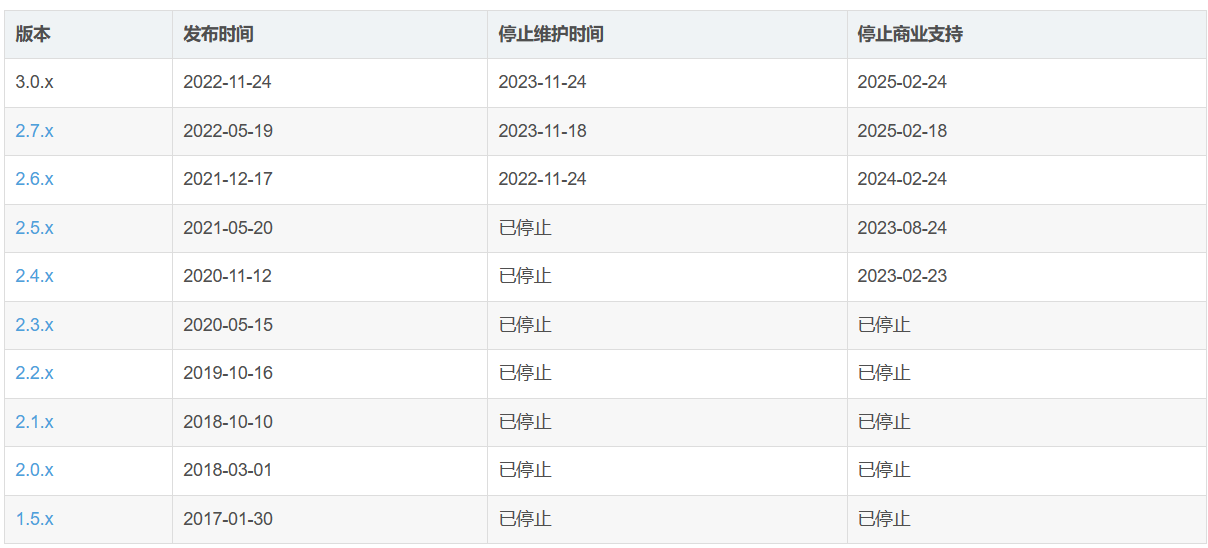
Spring Boot 3.0正式发布及新特性解读
目录 【1】Spring Boot 3.0正式发布及新特性依赖调整升级的关键变更支持 GraalVM 原生镜像 Spring Boot 最新支持版本Spring Boo 版本版本 3.1.5前置系统清单三方包升级 Ref 个人主页: 【⭐️个人主页】 需要您的【💖 点赞关注】支持 💯 【1】Spring Boo…...
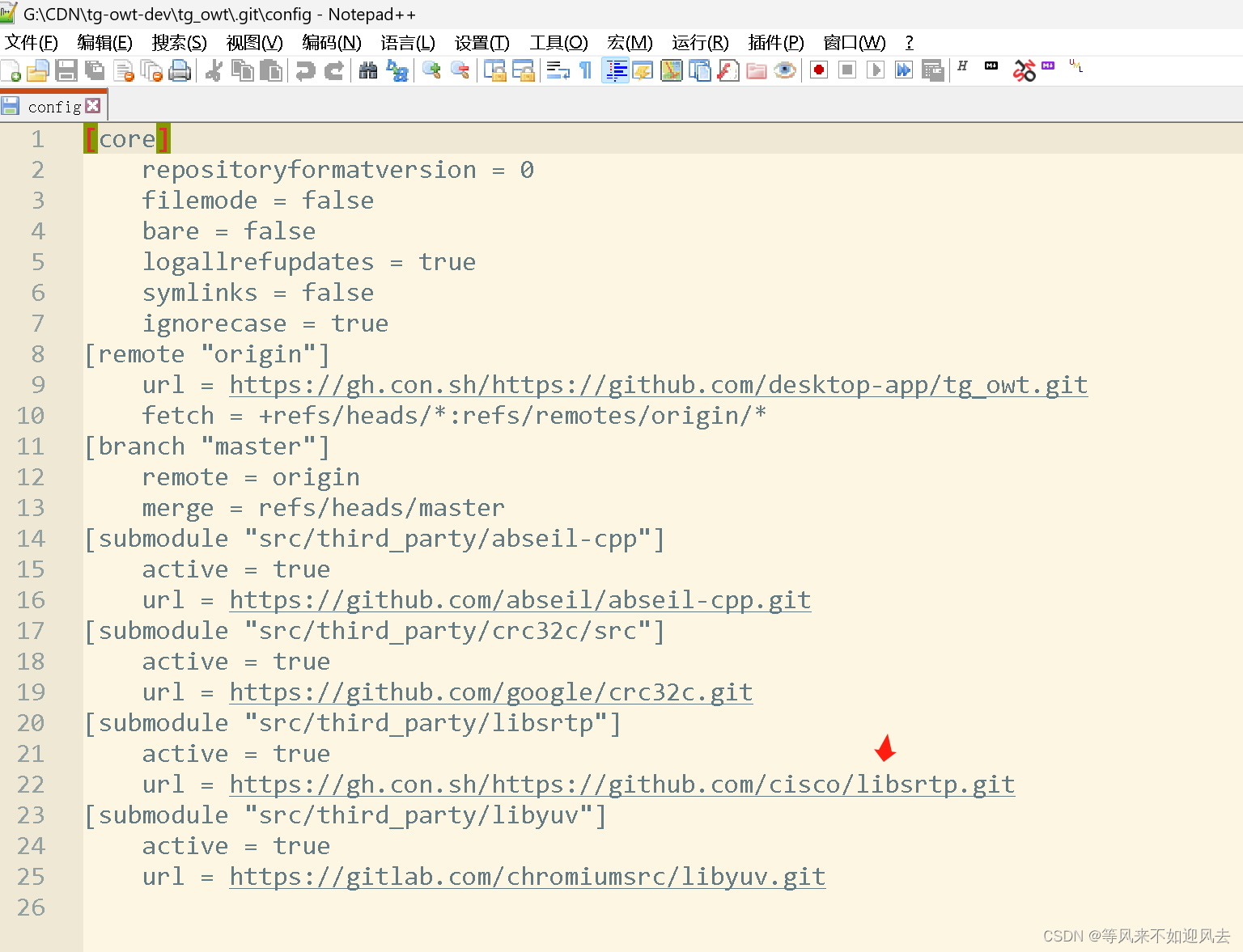
【tgowt】更新thirdparty
更新完毕后是这样的 之前有过构建但是不能用在owt-p2p项目中,会有崩溃? 【tgowt】cmake转ninja vs构建现在好像都更新到108了 submodule比较麻烦 只修改这里的还不行:一旦git submodule init 后,再改这里的似乎晚了?如果能成功clone就有生成 还必须要改这里的 折腾好几次才…...

金字塔原理小节
目录 第1章 为什么要用金字塔结构 一、归类分组,将思想组织成金字塔 二、奇妙的数字“7” 三、归类分组搭建金字塔 四、找出逻辑关系,抽象概括 五、自上而下表达,结论先行 第1章 为什么要用金字塔结构 如果受众希望通过阅读你的文章、听…...

osg点云加载与渲染
目录 效果 laslib 关键代码 完整代码 效果 las点云读取使用了laslib这个库。 laslib 关键代码 {// 这里演示读取一个 .txt 点云文件const char* lasfile path.c_str();std::ifstream ifs;ifs.open(lasfile, std::ios::in | std::ios::binary);liblas::ReaderFactory f;libl…...

后端架构选择:构建安全强大的知识付费小程序平台
构建知识付费小程序平台需要考虑后端架构,确保系统安全性、性能和可扩展性。以下是一些常见的后端技术和最佳实践,能帮助您构建强大且安全的知识付费小程序平台。 1. 服务器端语言和框架选择 选择流行、成熟的后端语言和框架,如Node.js、P…...

第四节(2):修改WORD中表格数据的方案
《VBA信息获取与处理》教程(10178984)是我推出第六套教程,目前已经是第一版修订了。这套教程定位于最高级,是学完初级,中级后的教程。这部教程给大家讲解的内容有:跨应用程序信息获得、随机信息的利用、电子邮件的发送、VBA互联网…...

Qt中对Udp数据打包发送和接收
有些小伙伴对怎么对Udp的数据打包不太清楚。下面我举例说明。 比如我们要发送一个Person的数据。可以先用一个结构把Person的数据封装。 struct Person {QString name;int age; };下面是udp客户端和服务器端完整的代码例子。 #ifndef UDPCLIENT_H #define UDPCLIENT_H#includ…...

回调地狱 与 Promise(JavaScript)
目录捏 前言一、异步编程二、回调函数三、回调地狱四、Promise1. Promise 简介2. Promise 语法3. Promise 链式 五、总结 前言 想要学习Promise,我们首先要了解异步编程、回调函数、回调地狱三方面知识: 一、异步编程 异步编程技术使你的程序可以在执行一…...

【Android】UI开发中的一些小细节笔记
序言 本篇笔记用于记录在UI界面编写时的一些很简单但是可能一时想不起来的一些小的知识点。(持续更新…) 正文 TextView 1.当文字比较多,需要多行显示的时候,设置每行文字之间的上下的间距 android:lineSpacingExtra根据需要调整这个值设置行间距 …...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
