动态规划基础篇(LeetCode每日一题计划)
爬楼梯
求所有爬楼梯的方案
方法一:f(x)=f(x-1)+f(x-2)
class Solution {public int climbStairs(int n) {int p=0,q=0,r=1;for(int i=0;i<n;i++){p=q;q=r;r=p+q;}return r;}
}方法二:动态规划
class Solution {
public:int climbStairs(int n) {int dp[46];dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++)dp[i]=dp[i-1]+dp[i-2];return dp[n];}
};
相关文章:
)
动态规划基础篇(LeetCode每日一题计划)
爬楼梯 求所有爬楼梯的方案 方法一:f(x)f(x-1)f(x-2) class Solution {public int climbStairs(int n) {int p0,q0,r1;for(int i0;i<n;i){pq;qr;rpq;}return r;} } 方法二:动态规划 class Solution { public:int climbStairs(int n) {int dp[46]…...

智慧商业:探索分布式云技术为企业创造商业价值,减少成本,提升生产力的秘诀!
我们可以试想一下,如果没有云计算,商业将会是什么样子? 对于这个问题的答案,许多人会认为它可能依旧是一个以实体为主行业。 云计算和多云战略的出现为在线购物带来了革命性的变化。 然而,如今多云所固有的复杂性仍然…...

Anaconda安装gdal
安装gdal 安装gdal,真是一波三折哇。pip、conda、c编译了等等,网上各种大佬的解决方法都试了试。咱就是说,都不行,很扯淡。甚至 使用conda install gdal 都显示安装成功了,但是 from osgeo import gdal; i…...

vite基础学习笔记:14.路由跳转(二)携带query参数
说明:自学做的笔记和记录,如有错误请指正 1. 路由跳转(携带query参数) (1)第一层路由(点击卡片路由跳转至新页面-携带query参数) 知识点: query传参对应的是path和qu…...

立体相机标定
相机成像过程中涉及的4个坐标系: 1、世界坐标系:由用户定义的三维世界坐标系,描述物体和相机在真实世界中的位置,原点可以任意选择。 2、相机坐标系:以相机的光心为坐标原点,X轴和Y轴平行于图像坐标系的X轴…...

mixin混合类的接口实现
mixin混合类的接口实现 应用 :CreateModelMixin,ListModelMixin,RetrieveModelMixin,DestroyModelMixin,UpdateModelMixin 简化工程代码。 from rest_framework.generics import GenericAPIView from rest_framework.mixins import CreateModelMixin,ListModelMixi…...

前端小技巧: TS实现EventBus自定义事件
关于EventBus事件总线 事件总线,实现 on, once, emit, off on, once 是注册函数,存储起来emit时找到对应的函数,执行off找到对应的函数,从对象中删除 注意 区分on和onceon绑定的事件可连续执行,除非offonce绑定的函数…...
Django之三板斧的使用,全局配置文件介绍,request对象方法,pycharm链接数据库,Django链接数据库,ORM的增删改查
【1】三板斧(3个方法)的使用 Httpresponse() 括号内写什么字符串,返回的就是什么字符串返回的是字符串 render(request, 静态文件 ) request是固定的静态文件是写在templates文件夹里面的,如,HTML文件 redirect( 重定向的地址 ) 重…...
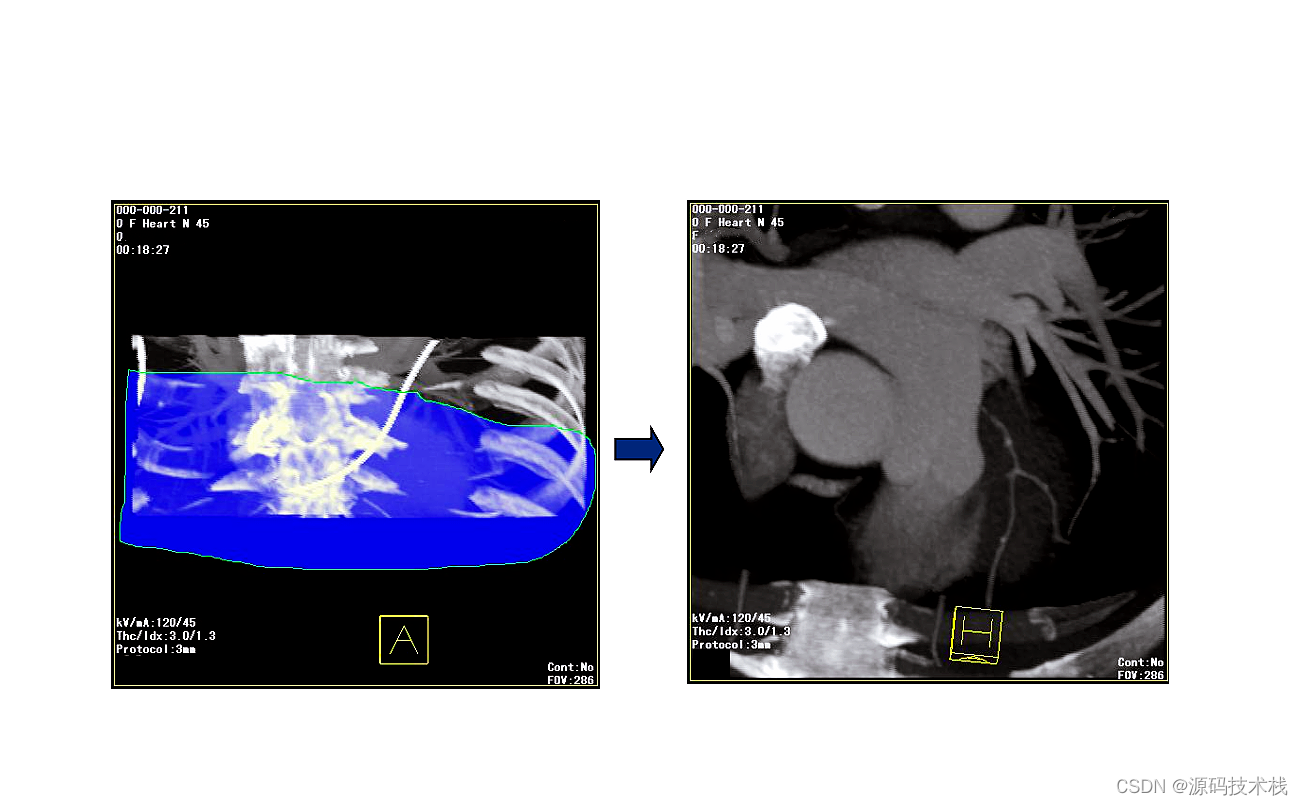
医学影像系统源码(MRI、CT三维重建)
一、MRI概述 核磁共振成像(英语:Nuclear Magnetic Resonance Imaging,简称NMRI),又称自旋成像(英语:spin imaging),也称磁共振成像(Magnetic Resonance Imag…...
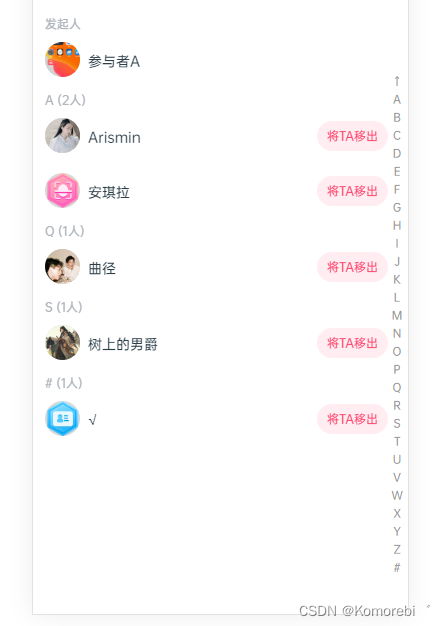
【uniapp】仿微信通讯录列表实现
效果图 代码实现 <view class"main-container"><!-- 成员列表 --><scroll-viewclass"member-list":style"computedHeight":scroll-y"true":enable-back-to-top"true":scroll-with-animation"true"…...

[MT8766][Android12] 增加应用安装白名单或者黑名单
文章目录 开发平台基本信息问题描述解决方法 开发平台基本信息 芯片: MT8766 版本: Android 12 kernel: msm-4.19 问题描述 在项目开发的时候,经常有一些客户,要求系统安装应用的时候需要进行验签;也就是系统默认不允许任何应用安装&#…...
游戏公司数据分析师必备知识(持续补充中...)
1.如何撰写专题报告? ①原则 只有一个主题:即使不讲ppt,业务方也能看得懂行文通俗简单易懂:学习产品经理平常是如何写报告的明确的数据结论和落地项先行:跟业务方多沟通数据结论,让他们给出落地项 ②结构…...

intellj 开发软件插件
IDEA: .ignore Alibaba Java Coding Guidelines(XenoAmess TPM) Chinese (Simplified) Language Pack / 中文语言包 CodeGlance Pro Gitee Grep Console Json Formatter Maven Helper Nyan Progress Bar One Dark theme Python Rainbow Brackets Resource Bundle Ed…...

leetCode 493 翻转对
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。你需要返回给定数组中的重要翻转对的数量。 未完待续~...
“辛巴猫舍”内网渗透、提权、撞库学习笔记
前言: 在拿到靶机时,我们最先需要做的是信息收集,包括不限于:C段扫描,端口探测,指纹识别,版本探测等。其次就是 漏洞挖掘、漏洞利用、提权、维持权限、日志清理、留下后门。 以上就是渗透的基本…...
粤嵌实训医疗项目--day06(Vue + SpringBoot)
往期回顾 粤嵌实训医疗项目(小组开发)--day05-CSDN博客粤嵌实训医疗项目--day04(Vue SpringBoot)-CSDN博客粤嵌实训医疗项目--day03(Vue SpringBoot)-CSDN博客粤嵌实训医疗项目day02(Vue SpringBoot)-CS…...

SPSS二元Logistic回归
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…...
前端-第一部分-HTML
一.初识HTML 1.1 HTML 简介 HTML 全称为 HyperText Mark-up Language,翻译为超文本标签语言,标签也称作标记或者元素。HTML 是目前网络上应用最为广泛的技术之一,也是构成网页文档的主要基石之一。HTML文本是由 HTML 标签组成的描述性文本&a…...
六度空间(C++)
目录 题目: 输入、输出格式: 代码: 运行结果: 题目: 输入、输出格式: 代码: #include<iostream> #include<algorithm> using namespace std; int g[10005][10005]; float n…...

记录undefined reference to `SSLv3_client_method‘错误笔记
libcurl.a(libcurl_la-openssl.o): in function ossl_connect_step1: openssl.c:(.text0x3ca8): undefined reference to SSLv3_client_method 我个人环境原因:编译选项指定了某个openssl目录,此目录下有libcrypto.a libssl.a 解决方法:…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
