每天一道算法题:40. 组合总和 II
难度
中等
题目
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]
提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
思路
和 39 题类似但是不能有重复的解,使用回溯试探法,但是过程要考虑去重。
数组中可能出现重复的数字,但是结果中不能出现重复的解,在处理过程中就要进行去重和剪枝。首先对 candidates 数组进行排序,在递归的过程中,当发现当前元素与前一个元素相同,并且前一个元素已经被考虑过(不在当前组合中),就跳过当前元素。
从数组的第一个元素开始,依次考虑是否选择该元素,再递归地考虑下一个元素,每个数字只能使用一次,因此在递归调用时,下一轮搜索的起始位置应该是当前位置的下一个位置。
代码
"""
10,1,2,7,6,1,5
8如果不排序的情况(10) > 8
1 2 7 > 8
1 2 6 > 8
1 2 1 5 > 8
1 2 5 = 81 7 = 8
1 6 1 = 8
1 1 5 遍历完成
1 5 遍历完成2 7 > 8
2 6 = 8
2 1 5 = 8 重复了 去重的方法 就是将所有的子集排序后,再进行去重,这样是再将所有的接过遍历完成之后,才能去重,效率非常低
2 52 7 > 8
2 6 = 8
2"""class Solution:def combinationSum2(self, candidates, target):self.candidates = candidates# 先对所有元素进行排序,再递归过程中进行去重,如果相邻的两个值相同,并且前一个值已经选过了,就不会选self.candidates.sort()self.target = targetself.length = len(self.candidates)self.cache = []self.result = []self.backtrack(0, [], self.target)print(self.result)return self.resultdef backtrack(self, start, tmp, target):# start 在当前层遍历的开始位置# tmp 记录临时值的栈# target 目标值,当目标值为0是 就可以终止递归# 当目标值为0的时候就终止递归,记录此时的组合if target == 0:self.result.append(tmp[:])returnfor i in range(start, self.length):# 在同一层遍历的时候,如果两个相邻的元素相同,就跳过 使用i-1就说明 上一个位置的值已经被选过了# i > start 因为要和前一个元素比较,所以i的值必须时大于start的,不然会越界if i > start and self.candidates[i] == self.candidates[i - 1]:continue# 如果当前值比目标值小 或者 相等的时候,才去递归下一层,不然直接跳过if target >= self.candidates[i]:tmp.append(self.candidates[i])# 集合中 每各元素只能添加一次,所以添加完当前的元素后,去下一层试探的时候只能从下一位开始遍历,所以下一层的开始位置就是i+1self.backtrack(i + 1, tmp, target - self.candidates[i])tmp.pop()if __name__ == '__main__':candidates = [10, 1, 2, 7, 6, 1, 5]target = 8# candidates = [2, 5, 2, 1, 2]# target = 5s = Solution()s.combinationSum2(candidates, target)相关文章:

每天一道算法题:40. 组合总和 II
难度 中等 题目 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含重复的组合。 示例 1: 输入: candidat…...
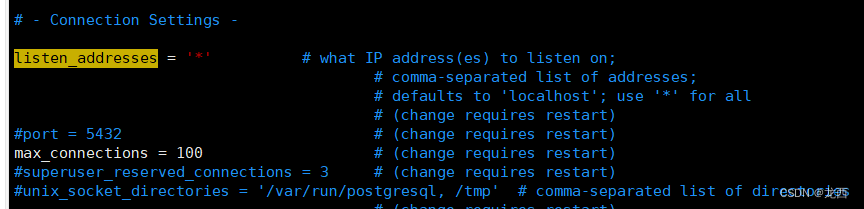
Centos7安装PostgreSQL 14
环境: Centos7安装PostgreSQL_14版本数据库; 打开官方网站:PostgreSQL: Linux downloads (Red Hat family) 一、 版本选择 复制、粘贴并运行如下脚本: 二、安装步骤 这些命令是在 CentOS 7.x 系统上安装和配置 PostgreSQL 14 的步…...

Shopee的折扣活动怎么分类?shopee设置折扣注意事项
旺季到来,Shopee会举办一些折扣活动来吸引客户,那么shopee的折扣活动怎么分类,shopee设置折扣注意事项? shopee的折扣活动怎么分类? 满减活动:满减活动是虾皮常见的一种折扣形式。在这种活动中࿰…...
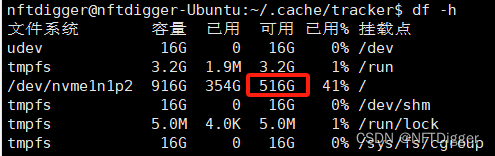
磁盘空间占用巨大的meta.db-wal文件缓存(tracker-miner-fs索引服务)彻底清除办法
磁盘命令参考本博客linux磁盘空间满了怎么办. 问题: 磁盘空间被盗 今天瞄了一下我的Ubuntu系统盘, nftdiggernftdigger-Ubuntu:~$ df -h 文件系统 容量 已用 可用 已用% 挂载点 udev 16G 0 16G 0% /dev tmpfs 3.2G 1.9…...
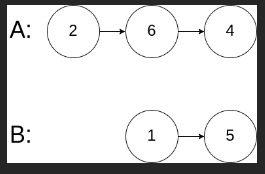
力扣:160. 相交链表(Python3)
题目: 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 图示两个链表在节点 c1 开始相交: 题目数据 保证 整个链式结构中不存在环。 注意,…...
实现))
【华为OD机试AB高分必刷题目】无名的搜索题(Java-优先搜索(DFS)实现)
🚀你的旅程将在这里启航!本专栏所有题目均包含优质解题思路,高质量解题代码,详细代码讲解,助你深入学习,高分通过! 文章目录 【华为OD机试AB高分必刷题目】无名的搜索题(Java-优先搜索(DFS)实现)题目描述解题思路Java题解代码代码OJ评判结果代码讲解寄语【华为OD机…...
通过内嵌的arg元素传递命令行参数)
ant 任务(task)通过内嵌的arg元素传递命令行参数
有的ant 任务将参数传递给其它的进程作为命令行参数。这可以通过内嵌的arg元素来实现。 例如: <exec executable"${browser}" spawn"true"><arg value"${file}"/> </exec>arg元素的部分属性说明: val…...
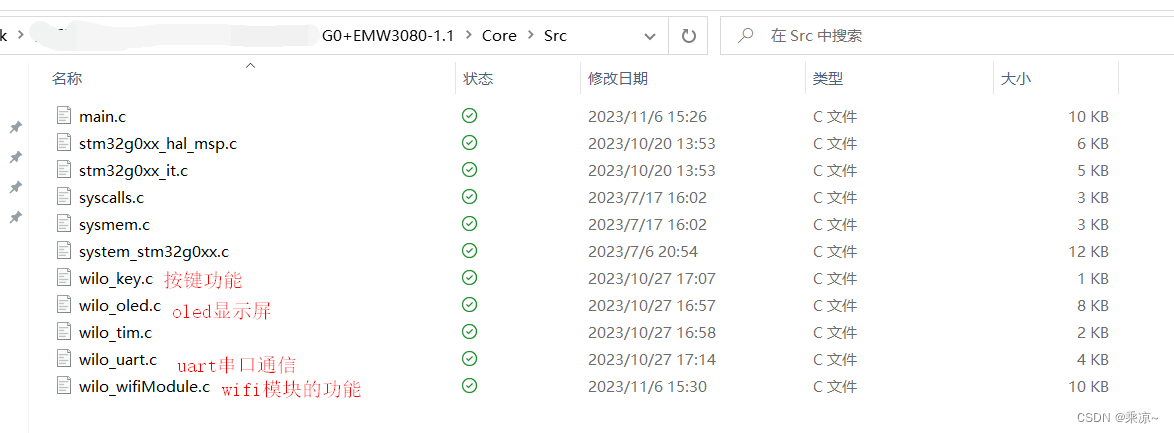
STM32G0+EMW3080+阿里云飞燕平台实现单片机WiFi智能联网功能(三)STM32G0控制EMW3080实现IoT功能
项目描述:该系列记录了STM32G0EMW3080实现单片机智能联网功能项目的从零开始一步步的实现过程;硬件环境:单片机为STM32G030C8T6;物联网模块为EMW3080V2-P;网联网模块的开发板为MXKit开发套件,具体型号为XCH…...
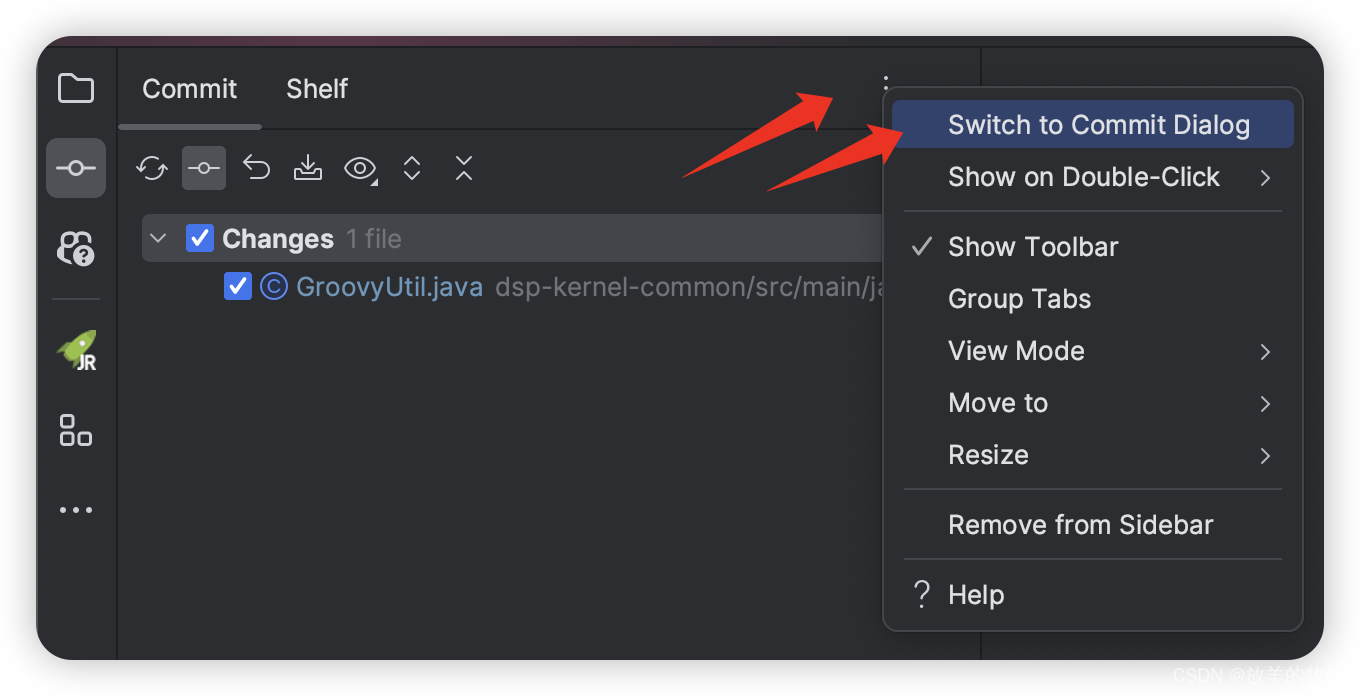
IntelliJ IDEA - Git Commit 后 Commit 窗口不消失解决方案
这个现象是在 2023 年版本后开始的,一开始以为是 Mac 系统的原因,后来发现原来 Windows 也这样,所以应该只跟 IDEA 版本有关 可以看到左侧 commit 后,这个侧边栏还在,按理讲在以前的版本是之前消失,这样使…...
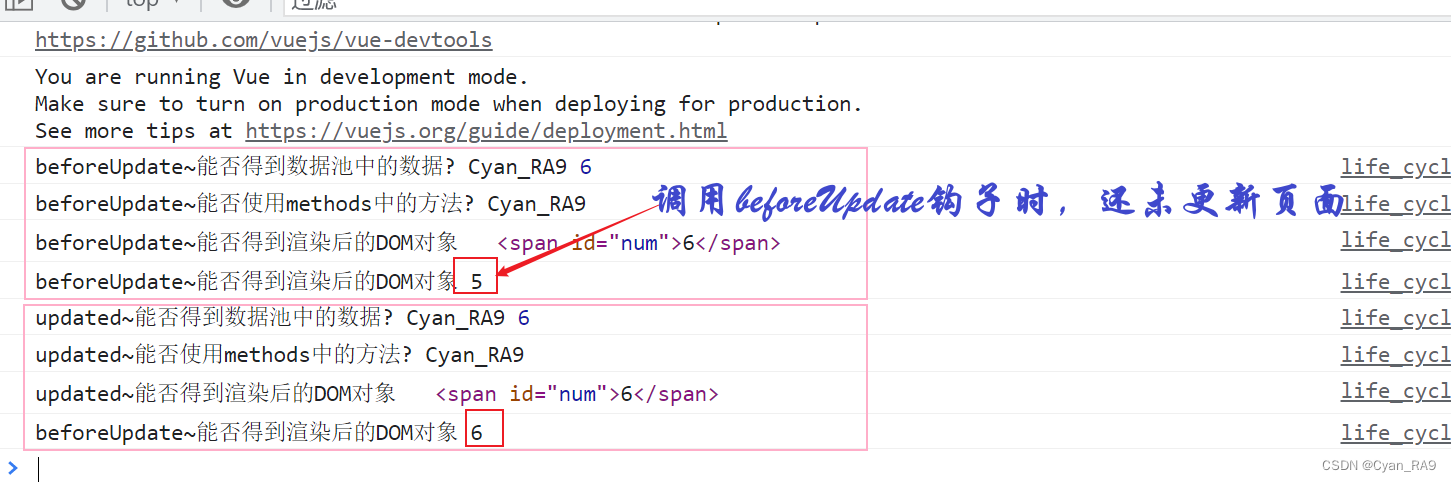
Vue 组件化编程 和 生命周期
目录 一、组件化编程 1.基本介绍 : 2.原理示意图 : 3.全局组件示例 : 4.局部组件示例 : 5.全局组件和局部组件的区别 : 二、生命周期 1.基本介绍 : 2.生命周期示意图 : 3.实例测试 : 一、组件化编程 1.基本介绍 : (1) 开发大型应用的时候,页面往往划分成…...

《数字图像处理-OpenCV/Python》连载(41)图像的旋转
《数字图像处理-OpenCV/Python》连载(41)图像的旋转 本书京东优惠购书链接:https://item.jd.com/14098452.html 本书CSDN独家连载专栏:https://blog.csdn.net/youcans/category_12418787.html 第 6 章 图像的几何变换 几何变换分…...

案例 - 拖拽上传文件,生成缩略图
直接看效果 实现代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>拖拽上传文件</title>&l…...

PHP 使用递归方式 将其二维数组整合为层级树 其中层级id 为一个uuid的格式 造成的诡异问题 已解决
不啰嗦 直接上源代码 <?php function findChildren($list, $p_id){$r array();foreach ($list as $k > $item) {if ($item[fid] $p_id) {unset($list[$k]);$length count($r);$r[$length] $item;if ($t findChildren($list, $item[id])) {$r[$length][children] …...

rv1126-rv1109-添加分区,定制固件,开机挂载功能
===================================================================== 修改分区: 这里是分区的txt文件选择; 这里是分区的划分,我这里回车了,方便看 FIRMWARE_VER: 8.1 MACHINE_MODEL: RV1126 MACHINE_ID: 007 MANUFACTURER: RV1126 MAGIC: 0x5041524B ATAG: 0x00200…...

一台电脑使用多个gitee账号,以及提交忽略部分文件
目录 编辑 一:前言 二:解决方法 三:提交gitee时忽略文件 一:前言 在开发中,我们拥有不止一个 gitee 账号,通常而言一个是公司的,一个是私人的。有时候我们在公司写了一些自己的东西&#…...

解析邮件文本内容; Mime文本解析; MimeStreamParser; multipart解析
原始文本 ------_Part_46705_715015081.1699589700255 Content-Type: text/html;charsetUTF-8 Content-Transfer-Encoding: base64PGh0bWwCiAgICA8aGVhZD4KICAgICAgICA8bWV0YSBodHRwLW VxdWl2PSJDb250ZW50LVR5cGUiIGNvbnRlbnQ9InRleHQvaHRt bDsgY2hhcnNldD1VVEYtOCICiAgICAgIC…...

获取请求IP以及IP解析成省份
某些业务需要获取请求IP以及将IP解析成省份之类的,于是我写了一个工具类,可以直接COPY /*** IP工具类* author xxl* since 2023/11/9*/ Slf4j public class IPUtils {/*** 过滤本地地址*/public static final String LOCAL_ADDRESS "127.0.0.1&quo…...
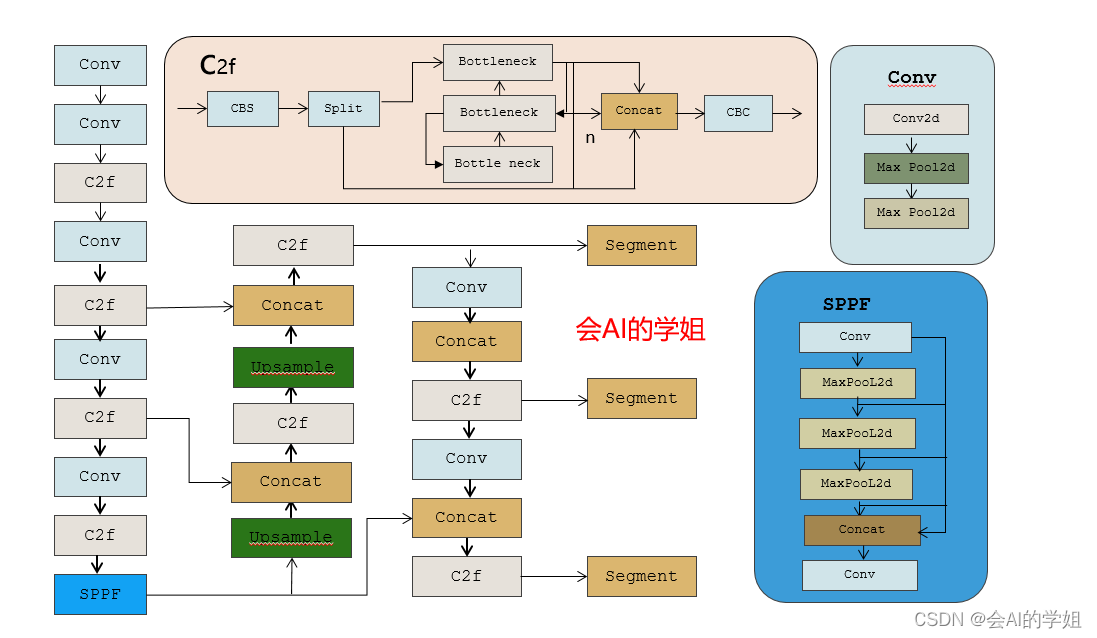
YOLOv8-seg改进:复现HIC-YOLOv5,HIC-YOLOv8-seg助力小目标分割
🚀🚀🚀本文改进:HIC-YOLOv8-seg:1)添加一个针对小物体的额外预测头,以提供更高分辨率的特征图2)在backbone和neck之间采用involution block来增加特征图的通道信息;3)在主干网末端加入 CBAM 的注意力机制; 🚀🚀🚀HIC-YOLOv8-seg小目标分割检测&复杂场景…...
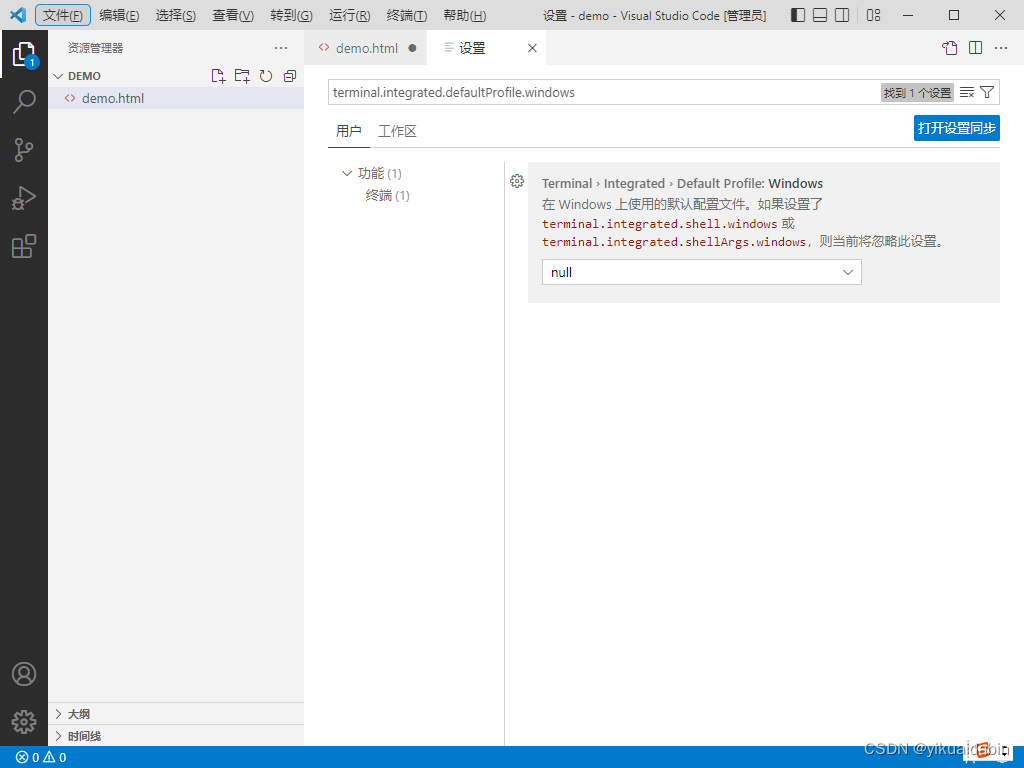
vscode 终端进程启动失败: shell 可执行文件“C:\Windows\System32\WindowsPower
vscode 终端进程启动失败: shell 可执行文件“C:\Windows\System32\WindowsPower 第一次用vscode,然后遇到这个问题,在设置里搜索 terminal.integrated.defaultProfile.windows 将这里的null改成"Command Prompt" 重启就可以了...
【中间件篇-Redis缓存数据库02】Redis高级特性和应用(慢查询、Pipeline、事务、Lua)
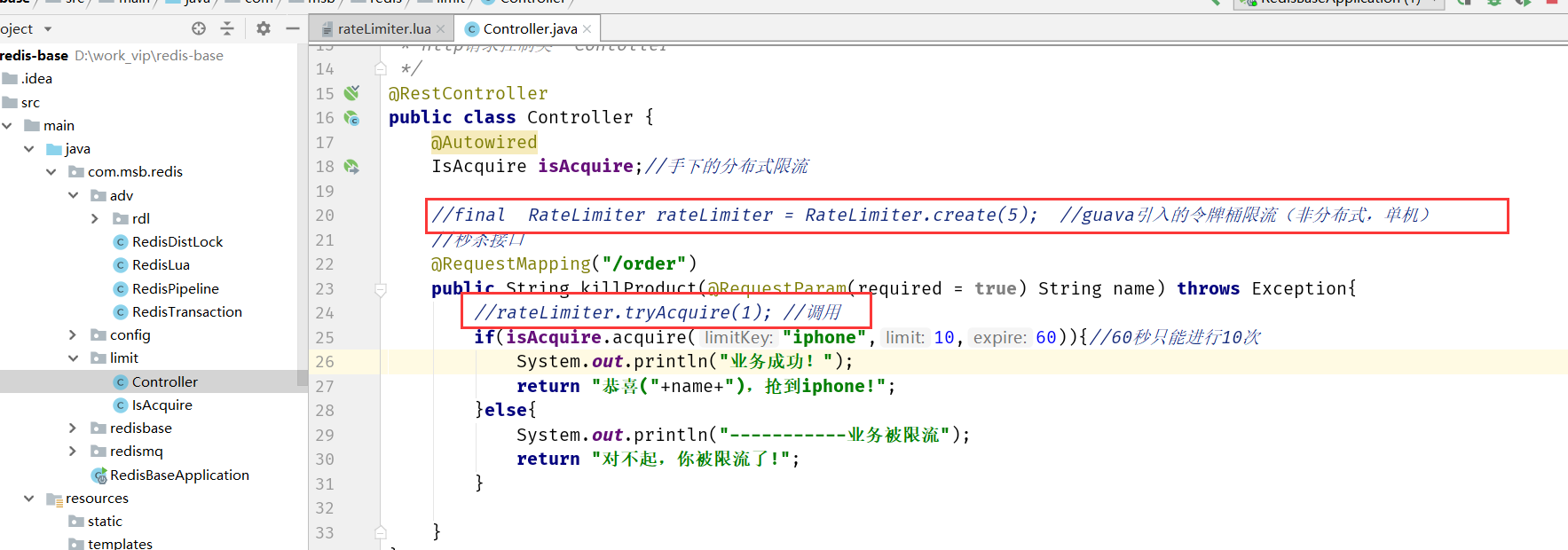
Redis高级特性和应用(慢查询、Pipeline、事务、Lua) Redis的慢查询 许多存储系统(例如 MySQL)提供慢查询日志帮助开发和运维人员定位系统存在的慢操作。所谓慢查询日志就是系统在命令执行前后计算每条命令的执行时间,当超过预设阀值,就将这条命令的相关…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
