【机器学习】Kmeans聚类算法
一、聚类简介
Clustering (聚类)是常见的unsupervised learning (无监督学习)方法,简单地说就是把相似的数据样本分到一组(簇),聚类的过程,我们并不清楚某一类是什么(通常无标签信息),需要实现的目标只是把相似的样本聚到一起,即只是利用样本数据本身的分布规律。
聚类算法可以大致分为传统聚类算法以及深度聚类算法:
传统聚类算法主要是根据原特征+基于划分/密度/层次等方法。
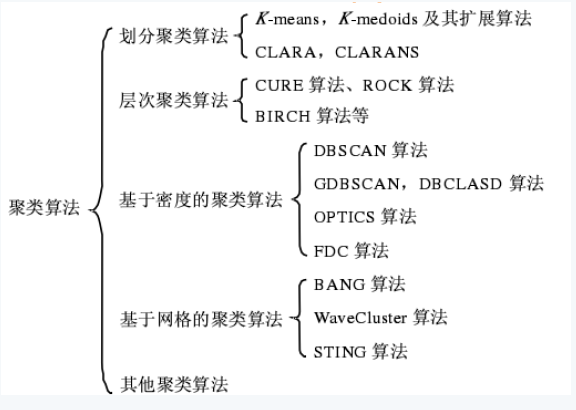
深度聚类方法主要是根据表征学习后的特征+传统聚类算法。
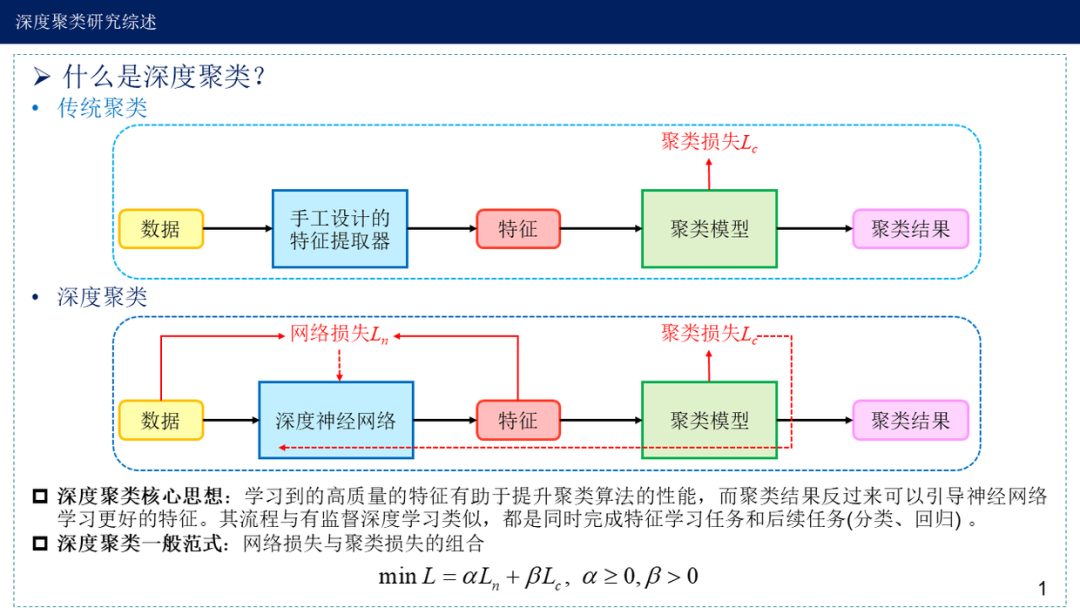
二、kmeans聚类原理
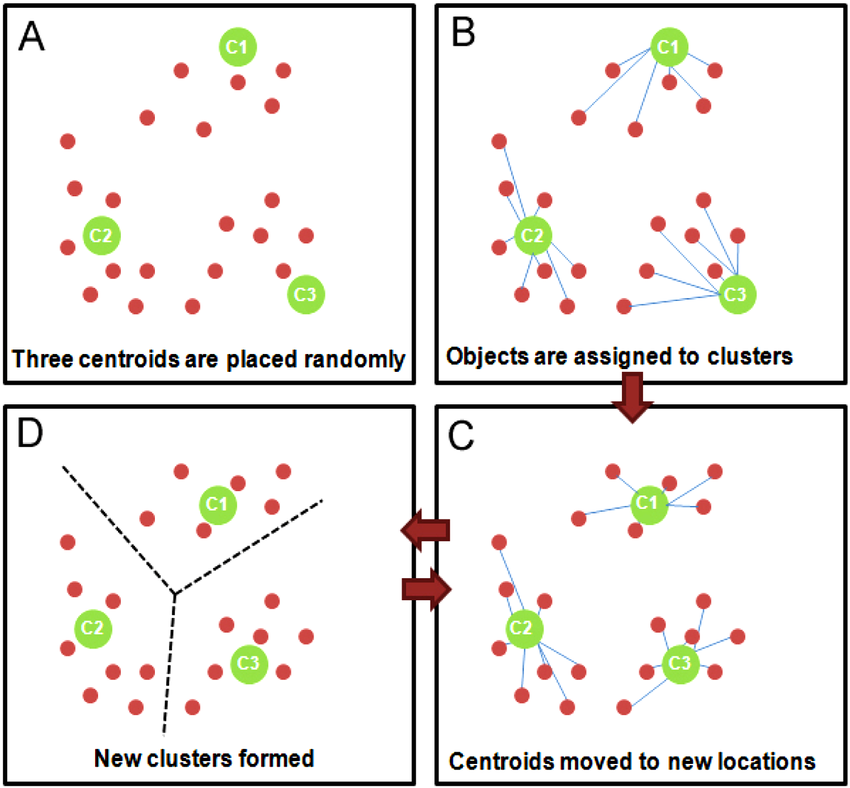
kmeans聚类可以说是聚类算法中最为常见的,它是基于划分方法聚类的,原理是先初始化k个簇类中心,基于计算样本与中心点的距离归纳各簇类下的所属样本,迭代实现样本与其归属的簇类中心的距离为最小的目标(如下目标函数)。
其优化算法步骤为:
1.随机选择 k 个样本作为初始簇类中心(k为超参,代表簇类的个数。可以凭先验知识、验证法确定取值);
2.针对数据集中每个样本 计算它到 k 个簇类中心的距离,并将其归属到距离最小的簇类中心所对应的类中;
3.针对每个簇类,重新计算它的簇类中心位置;
4.重复迭代上面 2 、3 两步操作,直到达到某个中止条件(如迭代次数,簇类中心位置不变等)。
.... 完整代码可见:https://github.com/aialgorithm/Blog 或文末阅读原文#kmeans算法是初始化随机k个中心点
random.seed(1)
center = [[self.data[i][r] for i in range(1, len((self.data)))] for r in random.sample(range(len(self.data)), k)]#最大迭代次数iters
for i in range(self.iters):class_dict = self.count_distance() #计算距离,比较个样本到各个中心的的出最小值,并划分到相应的类self.locate_center(class_dict) # 重新计算中心点#print(self.data_dict)print("----------------迭代%d次----------------"%i)print(self.center_dict) #聚类结果{k:{{center:[]},{distance:{item:0.0},{classify:[]}}}}if sorted(self.center) == sorted(self.new_center):breakelse:self.center = self.new_center
...
可见,Kmeans 聚类的迭代算法实际上是 EM 算法,EM 算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题。
在 Kmeans 中的隐变量是每个类别所属类别。Kmeans 算法迭代步骤中的 每次确认中心点以后重新进行标记 对应 EM 算法中的 E 步 求当前参数条件下的 Expectation 。而 根据标记重新求中心点 对应 EM 算法中的 M 步 求似然函数最大化时(损失函数最小时)对应的参数 。EM 算法的缺点是容易陷入局部极小值,这也是 Kmeans 有时会得到局部最优解的原因。
三、选择距离度量
kmeans 算法是基于距离相似度计算的,以确定各样本所属的最近中心点,常用距离度量有曼哈顿距离和欧式距离,具体可以见文章【全面归纳距离和相似度方法(7种)】
曼哈顿距离 公式:
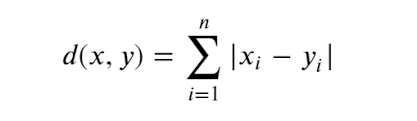
欧几里得距离 公式:
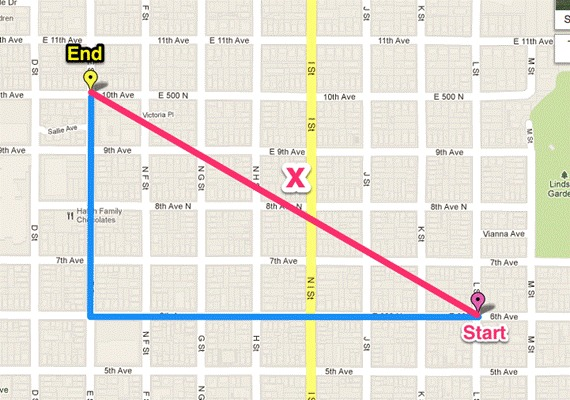
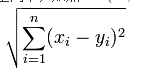 曼哈顿、欧几里得距离的计算方法很简单,就是计算两样本(x,y)的各个特征i间的总距离。如下图(二维特征的情况)蓝线的距离即是曼哈顿距离(想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”,也称为城市街区距离),红线为欧几里得距离:
曼哈顿、欧几里得距离的计算方法很简单,就是计算两样本(x,y)的各个特征i间的总距离。如下图(二维特征的情况)蓝线的距离即是曼哈顿距离(想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”,也称为城市街区距离),红线为欧几里得距离:
四、k 值的确定
kmeans划分k个簇,不同k的情况,算法的效果可能差异就很大。K值的确定常用:先验法、手肘法等方法。
先验法
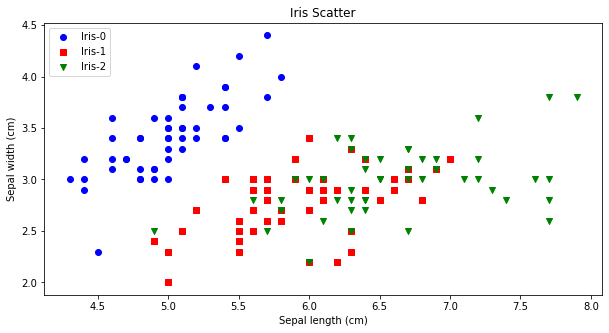
先验比较简单,就是凭借着业务知识确定k的取值。比如对于iris花数据集,我们大概知道有三种类别,可以按照k=3做聚类验证。从下图可看出,对比聚类预测与实际的iris种类是比较一致的。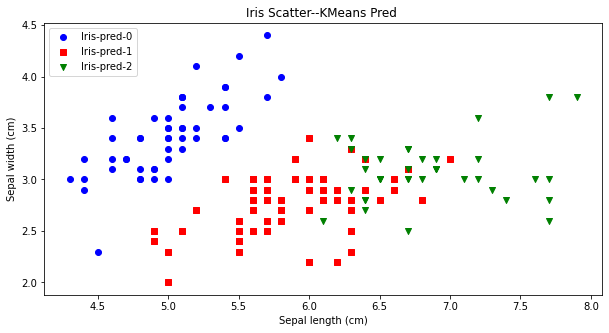
手肘法
可以知道k值越大,划分的簇群越多,对应的各个点到簇中心的距离的平方的和(类内距离,WSS)越低,我们通过确定WSS随着K的增加而减少的曲线拐点,作为K的取值。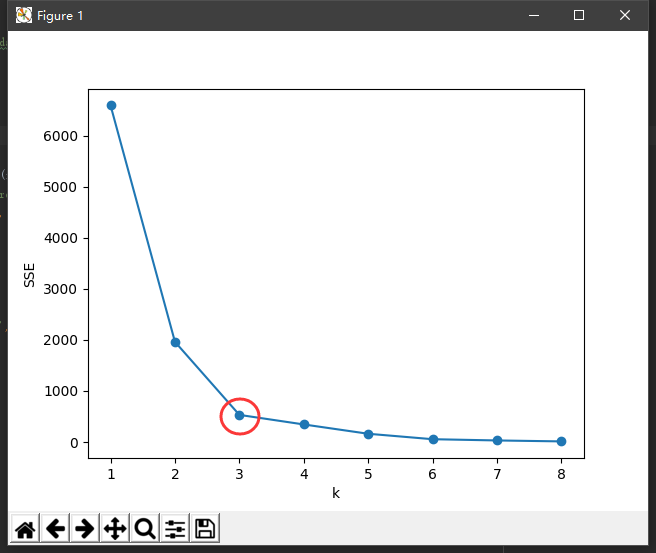
手肘法的缺点在于需要人为判断不够自动化,还有些其他方法如:
使用 Gap statistic 方法,确定k值。
验证不同K值的平均轮廓系数,越趋近1聚类效果越好。
验证不同K值的类内距离/类间距离,值越小越好。
ISODATA算法:它是在k-均值算法的基础上,增加对聚类结果的“合并”和“分裂”两个操作,确定最终的聚类结果。从而不用人为指定k值。
五、Kmeans的缺陷
5.1 初始化中心点的问题
kmeans是采用随机初始化中心点,而不同初始化的中心点对于算法结果的影响比较大。所以,针对这点更新出了Kmeans++算法,其初始化的思路是:各个簇类中心应该互相离得越远越好。基于各点到已有中心点的距离分量,依次随机选取到k个元素作为中心点。离已确定的簇中心点的距离越远,越有可能(可能性正比与距离的平方)被选择作为另一个簇的中心点。如下代码。
# Kmeans ++ 算法基于距离概率选择k个中心点# 1.随机选择一个点center = []center.append(random.choice(range(len(self.data[0]))))# 2.根据距离的概率选择其他中心点for i in range(self.k - 1):weights = [self.distance_closest(self.data[0][x], center) for x in range(len(self.data[0])) if x not in center]dp = [x for x in range(len(self.data[0])) if x not in center]total = sum(weights)#基于距离设定权重weights = [weight/total for weight in weights]num = random.random()x = -1i = 0while i < num :x += 1i += weights[x]center.append(dp[x])center = [self.data_dict[self.data[0][center[k]]] for k in range(len(center))]
5.2 核Kmeans
基于欧式距离的 Kmeans 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 Kmeans 算法,是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
5.3 特征类型
kmeans是面向数值型的特征,对于类别特征需要进行onehot或其他编码方法。此外还有 K-Modes 、K-Prototypes 算法可以用于混合类型数据的聚类,对于数值特征簇类中心我们取得是各特征均值,而类别型特征中心取得是众数,计算距离采用海明距离,一致为0否则为1。
5.4 特征的权重
聚类是基于特征间距离计算,计算距离时,需要关注到特征量纲差异问题,量纲越大意味这个特征权重越大。假设各样本有年龄、工资两个特征变量,如计算欧氏距离的时候,(年龄1-年龄2)² 的值要远小于(工资1-工资2)² ,这意味着在不使用特征缩放的情况下,距离会被工资变量(大的数值)主导。因此,我们需要使用特征缩放来将全部的数值统一到一个量级上来解决此问题。通常的解决方法可以对数据进行“标准化”或“归一化”,对所有数值特征统一到标准的范围如0~1。
归一化后的特征是统一权重,有时我们需要针对不同特征赋予更大的权重。假设我们希望feature1的权重为1,feature2的权重为2,则进行0~1归一化之后,在进行类似欧几里得距离(未开根号)计算的时候,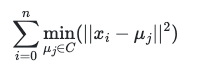 我们将feature2的值乘根号2就可以了,这样feature2对应的上式的计算结果会增大2倍,从而简单快速的实现权重的赋权。如果使用的是曼哈顿距离,特征直接乘以2 权重也就是2 。
我们将feature2的值乘根号2就可以了,这样feature2对应的上式的计算结果会增大2倍,从而简单快速的实现权重的赋权。如果使用的是曼哈顿距离,特征直接乘以2 权重也就是2 。
如果类别特征进行embedding之后的特征加权,比如embedding为256维,则我们对embedding的结果进行0~1归一化之后,每个embedding维度都乘以 根号1/256,从而将这个类别全部的距离计算贡献规约为1,避免embedding size太大使得kmeans的聚类结果非常依赖于embedding这个本质上是单一类别维度的特征。
5.5 特征的选择
kmeans本质上只是根据样本特征间的距离(样本分布)确定所属的簇类。而不同特征的情况,就会明显影响聚类的结果。当使用没有代表性的特征时,结果可能就和预期大相径庭!比如,想对银行客户质量进行聚类分级:交易次数、存款额度就是重要的特征,而如客户性别、年龄情况可能就是噪音,使用了性别、年龄特征得到的是性别、年龄相仿的客户!
对于无监督聚类的特征选择:
一方面可以结合业务含义,选择贴近业务场景的特征。
另一方面,可以结合缺失率、相似度、PCA等常用的特征选择(降维)方法可以去除噪音、减少计算量以及避免维度爆炸。再者,如果任务有标签信息,结合特征对标签的特征重要性也是种方法(如xgboost的特征重要性,特征的IV值。)
最后,也可以通过神经网络的特征表示(也就深度聚类的思想。后面在做专题介绍),如可以使用word2vec,将高维的词向量空间以低维的分布式向量表示。
参考文献:
1、https://www.bilibili.com/video/BV1H3411t7Vk?spm_id_from=333.999.0.0
2、https://zhuanlan.zhihu.com/p/407343831
3、https://zhuanlan.zhihu.com/p/78798251
相关文章:
【机器学习】Kmeans聚类算法
一、聚类简介 Clustering (聚类)是常见的unsupervised learning (无监督学习)方法,简单地说就是把相似的数据样本分到一组(簇),聚类的过程,我们并不清楚某一类是什么(通常无标签信息)࿰…...
getid3 获取视频时长
1、首先,我们需要先下载一份PHP类—getid3https://codeload.github.com/JamesHeinrich/getID3/zip/master 2.我在laravel6.0 中使用 需要在composer.json 自动加载 否则系统访问不到 在命令行 执行 composer dump-autoload $getID3 new \getID3();//视频文件需要放…...
如何知道一个程序为哪些信号注册了哪些信号处理函数?
https://unix.stackexchange.com/questions/379694/is-there-a-way-to-know-if-signals-are-present-in-your-application-and-which-sign 使用 strace...
34 mysql limit 的实现
前言 这里来看一下 我们常见的 mysql 分页的 limit 的相的处理 这个问题的主要是来自于 之前有一个需要处理 大数据量的数据表的信息, 将数据转移到 es 中 然后就是用了最简单的 “select * from tz_test limit $pageOffset, $pageSize ” 来分页处理 但是由于 数据表的数…...
jbase实现申明式事务
对有反射的语言,申明式事务肯定不可少。没必要没个人都try,catch写事务,写的不好的话还经常容易锁表,为此给框架引入申明式事务。申明式既字面意思,在需要事务的方法前面加一个申明,那么框架保证事务。 首…...
如何在在线Excel文档中规范单元格输入
在日常的工作中,我们常常需要处理大量的数据。为了确保数据的准确性和可靠性。我们需要对输入的数据进行规范化和验证。其中一个重要的方面是规范单元格输入。而数据验证作为Excel中一种非常实用的功能,它可以帮助用户规范单元格的输入,从而提…...
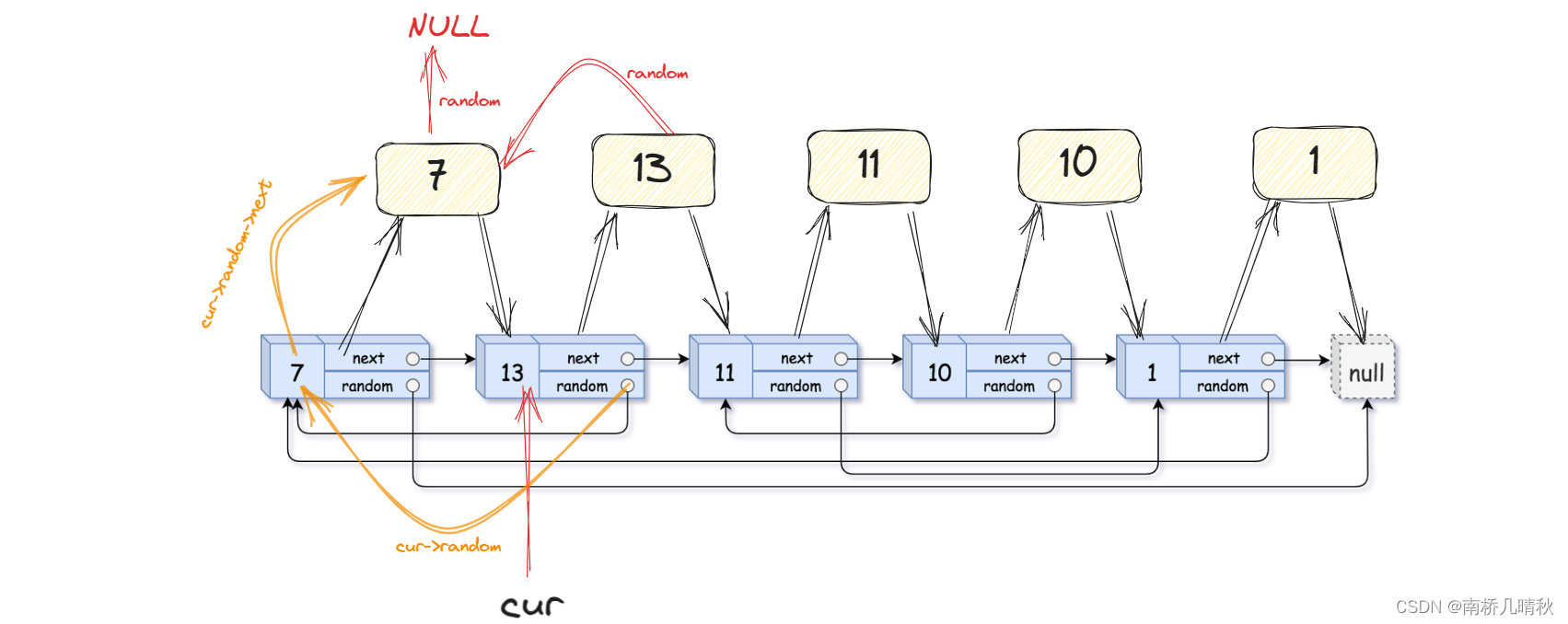
力扣138:随机链表的复制
力扣138:随机链表的复制 题目描述: 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成ÿ…...

C语言左移与右移学习
在学习左移与右移之前,我们首先要学习两种移位运算:逻辑移位和算数移位。 逻辑位移:移出去的位丢弃,空缺位用0补充。 算数位移:移出去的位丢弃,空缺位用符号位补充。 左移 左移是高位溢出,低…...

asp.net core mvc之 视图
一、在控制器中找到匹配视图,然后渲染成 HTML 代码返回给用户 public class HomeController : Controller {public IActionResult Index(){return View(); //默认找 Views/Home/Index.cshtml ,呈现给用户} } 二、指定视图 1、控制器 publ…...

ChatGLM3 tool_registry.py 代码解析
ChatGLM3 tool_registry.py 代码解析 0. 背景1. tool_registry.py 0. 背景 学习 ChatGLM3 的项目内容,过程中使用 AI 代码工具,对代码进行解释,帮助自己快速理解代码。这篇文章记录 ChatGLM3 tool_registry.py 的代码解析内容。 1. tool_re…...

js实现定时刷新,并设置定时器上限
定时器 在js中,有两种定时器: 倒计时定时器 倒计时定时器,也叫延时定时器或一次性定时器 功能:倒计时多长时间后执行某个动作 语法:setTimeout(function, timeout); 返回值:int类型,当前定时器…...

常用Linux命令
df -h #查看磁盘 kill -9 pid #强制关闭程序 ifconfig #查看网卡信息 last …...

【C++】获取指定点所在屏幕的尺寸
问题 多个显示器时,获取指定点所在的显示器的尺寸。 分析 之前整理过获取屏幕尺寸的方法:https://blog.csdn.net/m0_43605481/article/details/125024500多显示器时,需要用到GetSystemMetrics、EnumDisplayDevices、EnumDisplaySettings函…...
软文发布如何选择对应的媒体
企业做软文推广第一步,就是选择合适的媒体进行投放,然而许多企业不知道如何选择合适的媒体导致推广工作十分被动,无法取得效果,今天媒介盒子就来和大家分享,企业应该如何选择对应的媒体。 一、 媒体类型 根据软文类型…...
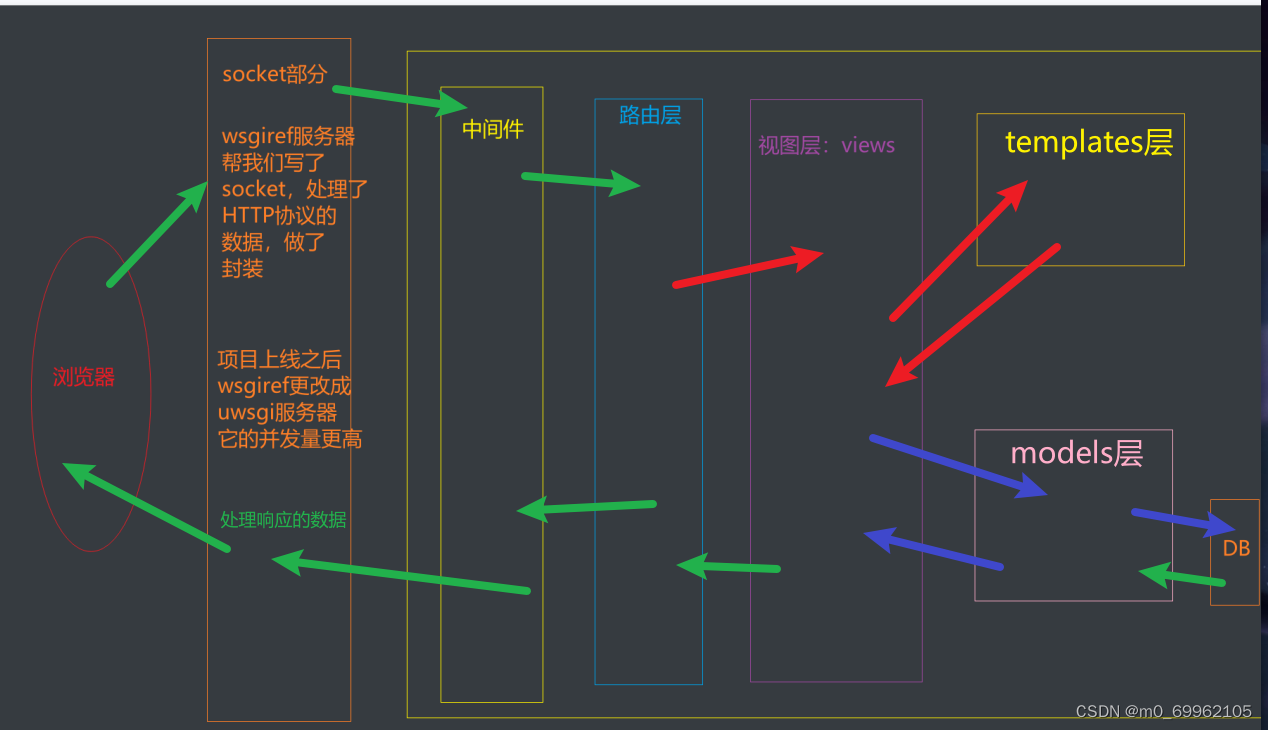
Django如何创建表关系,Django的请求声明周期流程图
【1】表与表之间的关系 一对一 左表的一条记录对应右表的一条记录,反之亦然 多对一 左表的一条记录对应右表的多条记录,反之不成立 多对多 左表的一条记录对应右表的多表记录,反之成立 【2】django中创建表关系 class Book(models.Model):t…...

微服务-我对Spring Clound的理解
官网:https://spring.io/projects/spring-cloud 官方说法:Spring Cloud 为开发人员提供了快速构建分布式系统中一些常见模式的工具(例如配置管理、服务发现、熔断器、智能路由、微代理、控制总线、一次性令牌、全局锁、领导选举、分布式会话…...
安防监控EasyCVR视频汇聚平台无法接入Ehome5.0是什么原因?该如何解决?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。安防平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存储、回放…...
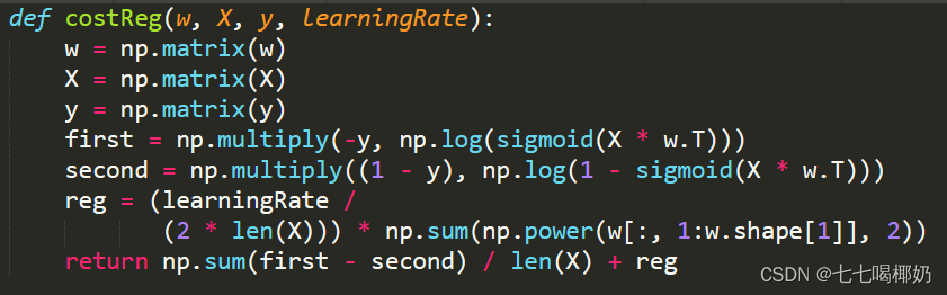
机器学习——逻辑回归
目录 一、分类问题 监督学习的最主要类型 二分类 多分类 二、Sigmoid函数 三、逻辑回归求解 代价函数推导过程(极大似然估计): 交叉熵损失函数 逻辑回归的代价函数 代价函数最小化——梯度下降: 编辑 正则化 四、逻辑…...
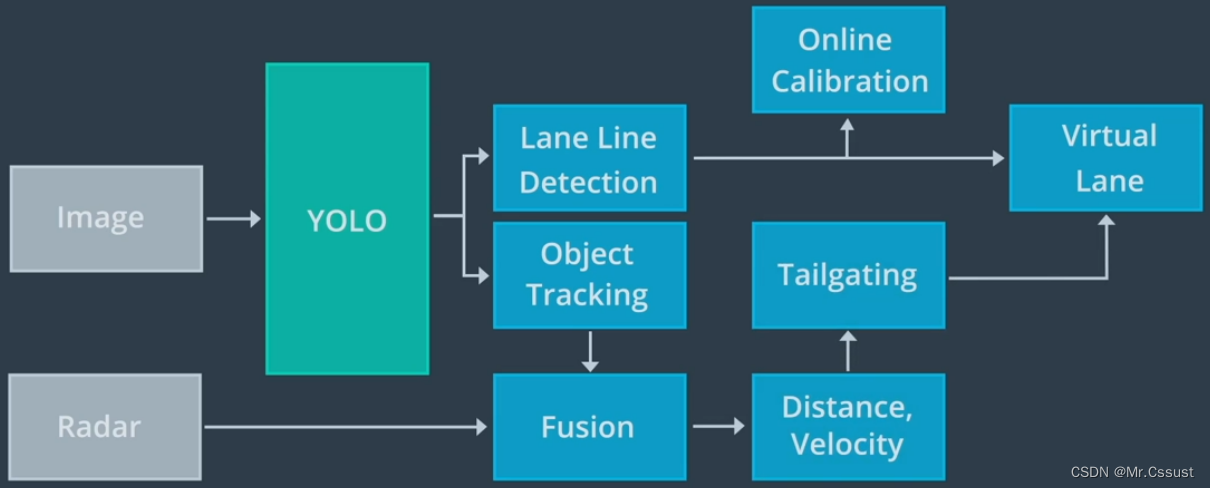
自动驾驶学习笔记(七)——感知融合
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo Beta宣讲和线下沙龙》免费报名—>传送门 文章目录 前言 感知融合 卡尔曼滤波 融合策略 实…...

【Java0基础学Java第八颗】 -- 继承与多态 -- 多态
8.继承与多态 8.2 多态8.2.1 多态的概念8.2.2 多态实现条件8.2.3 重写8.2.4 向上转型和向下转型8.2.5 向下转型8.2.6 多态的优缺点8.2.7 避免在构造方法中调用重写的方法 8.2 多态 8.2.1 多态的概念 通俗来说就是多种形态,具体点就是去完成某个行为,当…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
