【Linux】 awk命令使用
AWK 是一种处理文本文件的语言,是一个强大的文本分析工具。
之所以叫 AWK 是因为其取了三位创始人 Alfred Aho,Peter Weinberger, 和 Brian Kernighan 的 Family Name 的首字符。
语法
awk [选项] [文件]
awk [选项] [程序] [文件]awk命令 -Linux手册页

作者
UNIX awk的原始版本由贝尔实验室的Alfred Aho、Peter Weinberger和Brian Kernighan设计和实现。Brian Kernighan继续保持和增强它。
自由软件基金会的Paul Rubin和Jay Fenlason编写了gawk,以与第七版UNIX中分发的awk的原始版本兼容。约翰·伍兹贡献了许多错误修复。David Trueman在Arnold Robbins的贡献下,使gawk与新版本的UNIX awk兼容。阿诺德·罗宾斯是目前的维护者。
最初的DOS端口由Conrad Kwok和Scott Garfinkle完成。Scott Deifik是目前DOS的维护者。Pat Rankin负责VMS的港口,Michal Jaegermann负责Atari ST的港口。Kai Uwe Rommel在Darrel Hankerson的贡献和帮助下负责OS/2的港口。Andreas Buening现在维护OS/2端口。Fred Fish为Amiga提供支持,Martin Brown提供BeOS端口。Stephen Davies提供了最初的Tandem端口,Matthew Woehlke为Tandem的POSIX兼容系统提供了更改。拉尔夫·维尔登豪斯现在维护着那个港口。
命令选项及作用
执行令 awk --help
执行命令结果

参数
- -F fs or --field-separator fs 指定输入文件折分隔符,fs是一个字符串或者是一个正则表达式,如-F:。
- -v var=value or --asign var=value 赋值一个用户定义变量。
- -f scripfile or --file scriptfile 从脚本文件中读取awk命令。
- -mf nnn and -mr nnn 对nnn值设置内在限制,-mf选项限制分配给nnn的最大块数目;-mr选项限制记录的最大数目。这两个功能是Bell实验室版awk的扩展功能,在标准awk中不适用。
- -W compact or --compat, -W traditional or --traditional 在兼容模式下运行awk。所以gawk的行为和标准的awk完全一样,所有的awk扩展都被忽略。
- -W copyleft or --copyleft, -W copyright or --copyright 打印简短的版权信息。
- -W help or --help, -W usage or --usage 打印全部awk选项和每个选项的简短说明。
- -W lint or --lint 打印不能向传统unix平台移植的结构的警告。
- -W lint-old or --lint-old 打印关于不能向传统unix平台移植的结构的警告。
- -W posix 打开兼容模式。但有以下限制,不识别:/x、函数关键字、func、换码序列以及当fs是一个空格时,将新行作为一个域分隔符;操作符**和**=不能代替^和^=;fflush无效。
- -W re-interval or --re-inerval 允许间隔正则表达式的使用,参考(grep中的Posix字符类),如括号表达式[[:alpha:]]。
- -W source program-text or --source program-text 使用program-text作为源代码,可与-f命令混用。
- -W version or --version
运算符
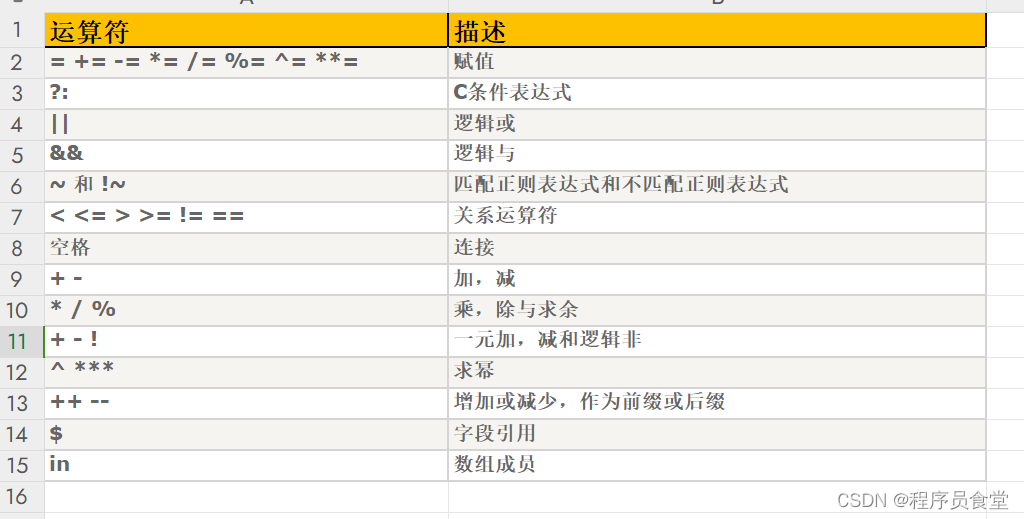
内建变量

常用命令示例
查看文本文件内容
cat test8.text 
命令:awk '{print}' 文件名
执行命令 : awk '{print}' test8.text
输出filename文件中的每一行文本。
命令:awk '{print $2 }' 文件名
执行命令 :awk '{print $2}' test8.text
打印filename文件中的第二列数据。

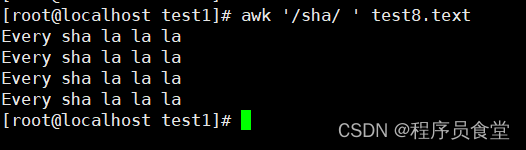
命令:awk '/pattern/{print}' 文件名
执行命令 : awk '/sha/{print}' test8.text
Awk命令还可以用于匹配输入数据中的特定文本。例如,如果我们想要匹配包含 “sha” 符串的行。
命令:awk -F
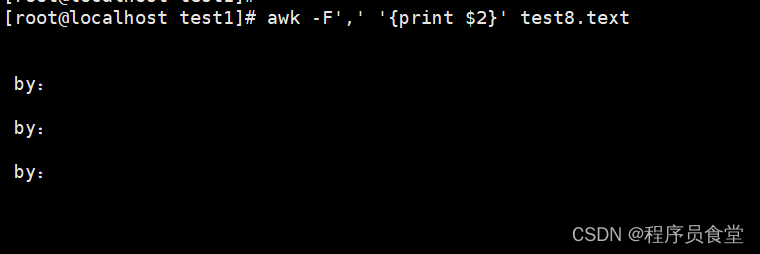
执行命令 : awk -F',' '{print $2}' test8.text
使用自定义分隔符使用-F选项。使用逗号作为分隔符。
输出filename文件中的第二列数据,以逗号作为分隔符。
命令:awk -v
执行命令 : awk -v a=1 '{print $1,$1+a}' test8.text
使用变量。

命令:awk -v
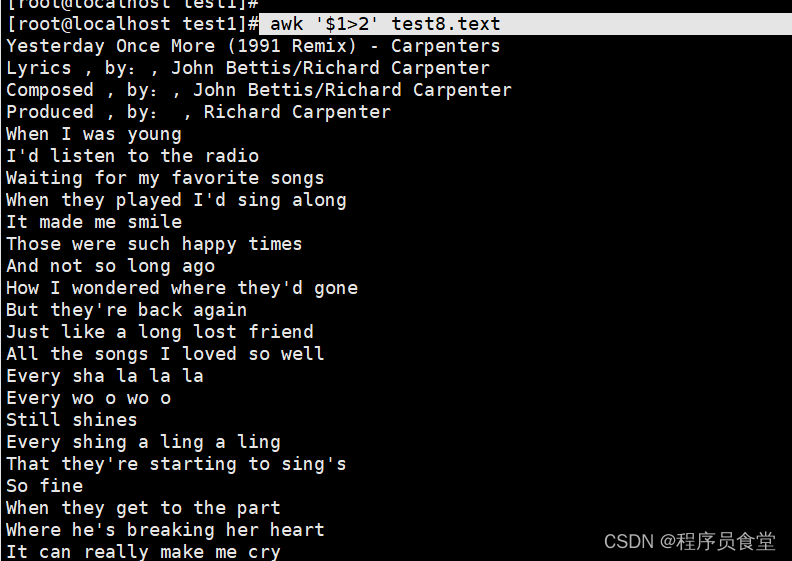
执行命令 : awk '$1>2' test8.text
过滤第一列大于2的行。
使用正则,字符串匹配
命令:输出第二列包含 "sha",并打印第二列与第四列
执行命令 : awk '$2 ~ /sha/ {print $2,$4}' test8.text
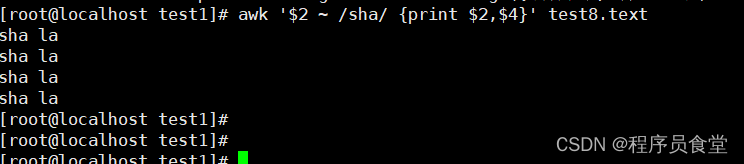
命令:~ 表示模式开始。// 中是模式。
执行命令 : awk '$2 ~ /sha/ {print $2,$4}' test8.text
输出包含 "sha" 的行。
相关文章:

【Linux】 awk命令使用
AWK 是一种处理文本文件的语言,是一个强大的文本分析工具。 之所以叫 AWK 是因为其取了三位创始人 Alfred Aho,Peter Weinberger, 和 Brian Kernighan 的 Family Name 的首字符。 语法 awk [选项] [文件] awk [选项] [程序] [文件] awk命令 -Linux手…...
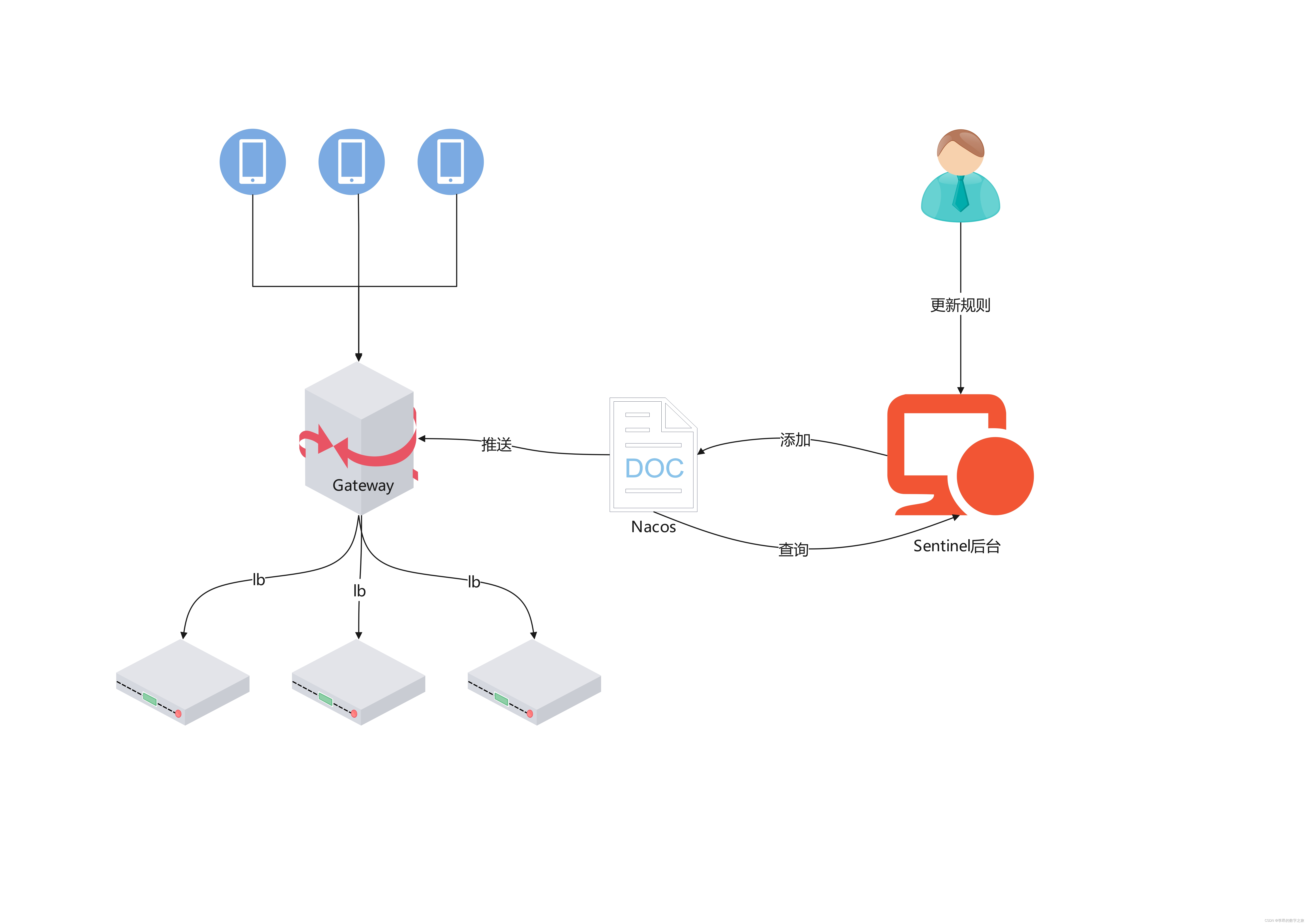
Sentinel网关限流
背景 在微服务架构下,每个服务的性能都不同,为避免出现流量洪峰将服务冲垮,需要依赖限流工具来保护服务的稳定性。sentinel是阿里提供的限流工具,社区活跃,功能也很全面,包含实时监控、流控、熔断等功能。…...

solidworks对电脑要求高吗?2023solidworks配置要求
solidworks对电脑要求高吗?SolidWorks是一款功能强大的三维CAD软件,对电脑配置有一定的要求。一般来说,运行SolidWorks需要的电脑配置包括较高的处理器性能、足够的内存和存储空间,以及一块性能良好的显卡。此外,对于大…...
)
搭建神经网络(torch.nn的用法)
零零碎碎总结了一些torch框架里面nn模块的用法,尤其是关于搭建神经网络的 nn.ModuleList nn.Module nn.Sequential nn.Linear nn.Dropout nn.Embedding nn.DataParallel() 将模型封装起来,便于在多个gpu上并行计算,训练或者推理 nn.…...
卡码网语言基础课 | 11. 句子缩写
目录 一、 字符串大小的比较 二、 ASCII码值 三、 基本框架代码 四、 解题思路 4.1 首字母问题 4.2 判定小写字母 4.3 小写字母转换为大写字母 五、空格判断 六、 代码模块化 6.1 满足的条件 6.2 代码完善 七、 题目解答 7.1 原始代码 7.2 改进代码 八、 拓展与…...

Surface RT 安装 Linux
零:起因 在家无事找出来一台老旧设备 Surface RT 一代的,系统最新是 Windows 8.1 arm版,应用商店都已经打不开了 虽说有破解方法,能运行些软件,但怎么说也不是任意安装,所以局限性还是相当的大࿰…...
C++中的函数重载:多功能而强大的特性
引言 函数重载是C编程语言中的一项强大特性,它允许在同一个作用域内定义多个同名函数,但这些函数在参数类型、个数或顺序上有所不同。本文将深入探讨函数重载的用法,以及它的优势和应用场景。 正文 在C中,函数重载是一项非常有…...
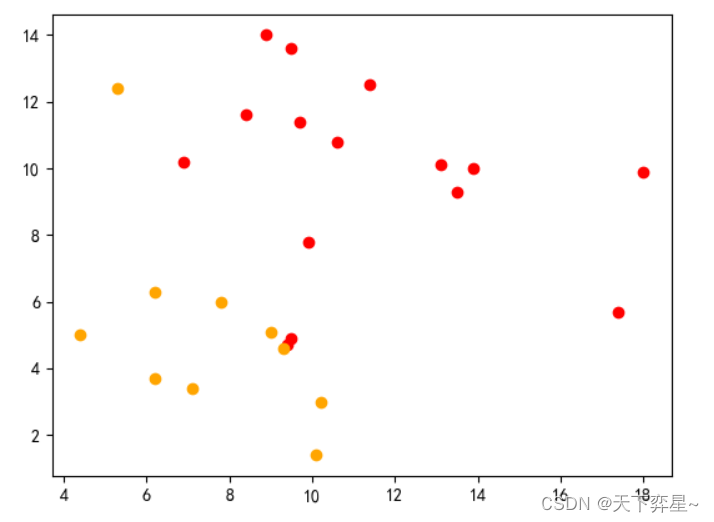
数据分析实战 | K-means算法——蛋白质消费特征分析
目录 一、数据及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 编辑 八、模型评价 九、模型调参与预测 一、数据及分析对象 txt文件——“protein.txt”,主要记录了25个国家的9个属性,主…...
HTTP协议详解-下(Tomcat)
如何构造 HTTP 请求 对于 GET 请求 地址栏直接输入点击收藏夹html 里的 link script img a…form 标签 通过 form 标签构造GET请求 <body><!-- 表单标签, 允许用户和服务器之间交互数据 --><!-- 提交的数据报以键值对的结果来组织 --><form action&quo…...

acwing算法基础之搜索与图论--prim算法
目录 1 基础知识2 模板3 工程化 1 基础知识 朴素版prim算法的关键步骤: 初始化距离数组dist,将其内的所有元素都设为正无穷大。定义集合S,表示生成树。循环n次:找到不在集合S中且距离集合S最近的结点t,用它去更新剩余…...

Amazon EC2 Serial Console 现已在其他亚马逊云科技区域推出
即日起,交互式 EC2 Serial Console 现也在以下区域推出:中东(巴林)、亚太地区(雅加达)、非洲(开普敦)、中东(阿联酋)、亚太地区(香港)…...
-39)
hdlbits系列verilog解答(100输入逻辑门)-39
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 构建一个具有 100 个输入in[99:0]的组合电路。 有 3 个输出: out_and: output of a 100-input AND gate. out_or: output of a 100-input OR gate. out_xor: output of a 100-input XOR gate. 二、verilog源…...

Python 中 Selenium 的屏幕截图
文章目录 使用 save_screenshot() 函数在 Python 中使用 selenium 捕获屏幕截图使用 get_screenshot_as_file() 函数在 Python 中使用 selenium 捕获屏幕截图使用 Screenshot-Selenium 包在 Python 中使用 selenium 捕获屏幕截图总结我们可以使用 Selenium 在自动化 Web 浏览器…...

scrapy发json的post请求
一 、scrapy发json的post请求: def start_requests(self):self.headers {Content-Type: application/json}json_data {"productName": "", "currentPage": "1", "recordNumber": "10", "langua…...
一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
目录 1解题思路: 2代码如下: 3运行结果: 4总结: 5介绍: 1解题思路: 利用循环(穷举法)来 对 所 需要的数 进行确定 2代码如下: #include <stdio.h>int main() …...
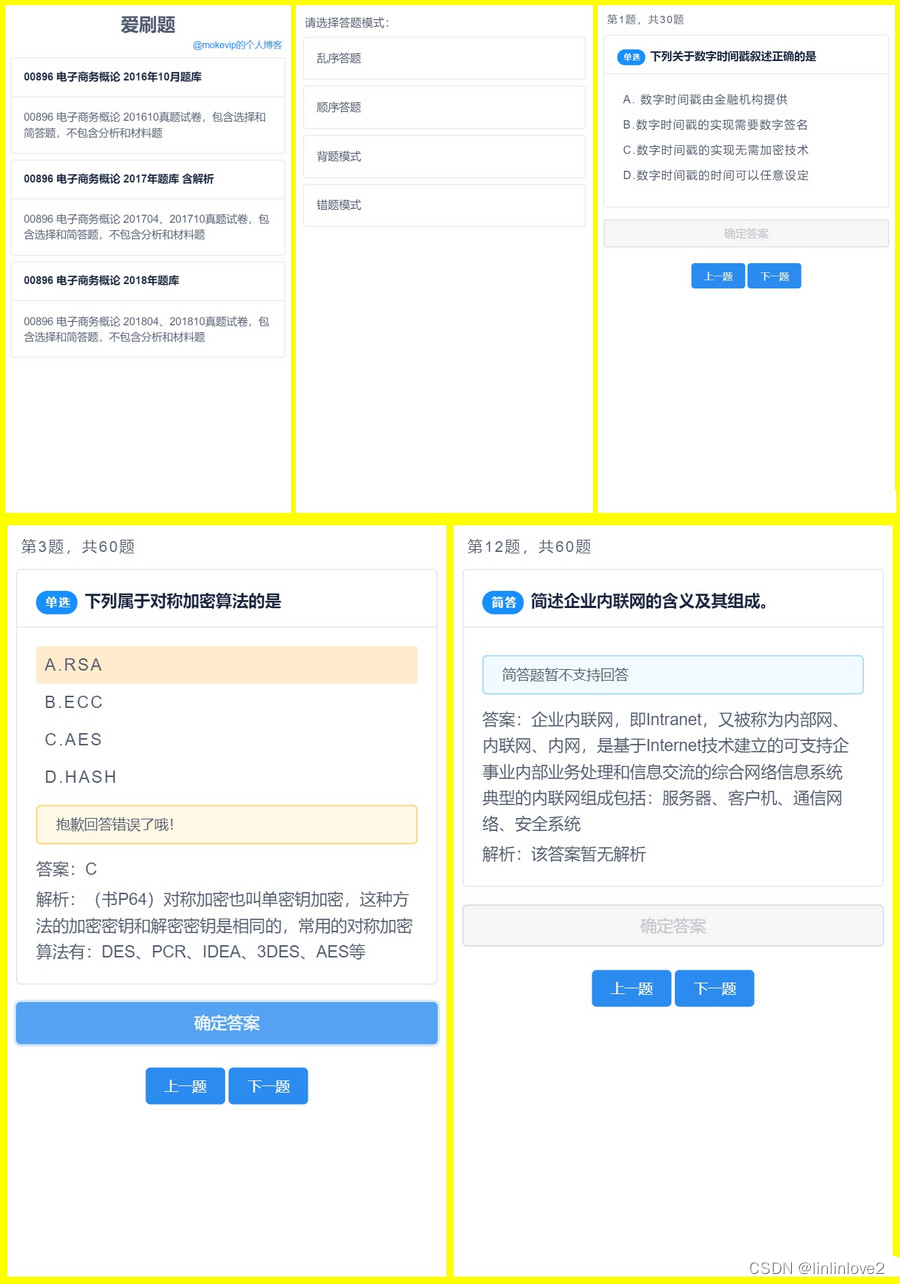
自主开发刷题应用网站H5源码(无需后端无需数据库)
该应用使用JSON作为题库的存储方式,层次清晰、结构简单易懂。 配套的word模板和模板到JSON转换工具可供使用,方便将题库从word格式转换为JSON格式。 四种刷题模式包括顺序刷题、乱序刷题、错题模式和背题模式,可以根据自己的需求选择适合的模…...

java 读取excel/word存入mysql
引入依赖 <!--poi--><dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>4.0.1</version></dependency><dependency><groupId>org.apache.poi</groupId><artif…...

11.(vue3.x+vite)组件间通信方式之ref与$parent、$children
前端技术社区总目录(订阅之前请先查看该博客) 示例效果 注: (1)ref 加在标签(div等)上,是拿到dom 对象 (2)ref加上组件上,拿到的是组件的引用 (3)让父组件获取子组件的数据或者方法需要通过defineExpose对外暴露,另外让父组件获取子组件的数据或者方法需要通过d…...

[工业自动化-12]:西门子S7-15xxx编程 - PLC从站 - ET200 SP系列详解
目录 一、概述 1.1 概述 二、系统组成 2.1 概述 2.2 与主站的通信接口模块 2.3 总线适配器 2.4 基座单元 2.5 电子模块 2.6 服务器模块 一、概述 1.1 概述 PLC ET200 SP 是西门子(Siemens)公司生产的一款模块化可编程逻辑控制器(PL…...

消息队列简介
消息队列 在认识rabbitMQ之前,我们需要先认识下消息队列。 消息队列,一般简称为MQ(Message Queue)。先不管消息(Message)这个词,先看看队列(Queue)。 队列就是一种先进先出的数据结构。 所以消息队列可以简单理解为&a…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
