【电路笔记】-节点电压分析和网状电流分析
节点电压分析和网状电流分析
文章目录
- 节点电压分析和网状电流分析
- 1、节点电压分析
- 1.1 概述
- 1.2 示例
- 2、网格电流分析
- 2.1 概述
- 2.2 示例
- 3、总结
正如我们在上一篇介绍电路分析基本定律的文章中所看到的,基尔霍夫电路定律 (KCL) 是计算任何电路中未知电压和电流的强大而高效的工具。 然而,基尔霍夫电路定律有时会带来重复性的不便,并且并不是分析更复杂电路的最快方法。
有两种基于基尔霍夫电路定律的方法可以简化并提高电路分析的效率:节点电压分析和网格电流分析。
我们在本文中分别分两节介绍这两种方法。 在每个部分中,都给出了一个真实的例子来说明如何进行这些分析。
1、节点电压分析
1.1 概述
节点电压分析 (NVA) 基于基尔霍夫电流定律,用于确定电路节点处的未知电压。 它由一系列要遵循的步骤组成,简要列出如下:
- 1)标记电路的基本节点,基本节点由三个或更多分支之间的连接点组成。
- 2)选择其中一个节点作为电路的参考。 大多数情况下,它是底部节点。
- 3)将支路中的电流表示为电压的函数。
- 4)在参考节点以外的每个节点写出基尔霍夫电流定律。
1.2 示例
假设有图1中所示的以下电子电路,我们将对其执行节点电压分析。 对于数值应用,我们取 S 1 = 10 V S_1=10V S1=10V, S 2 = 2 A S_2=2A S2=2A; R 1 = 1 Ω R_1=1\Omega R1=1Ω, R 2 = 5 Ω R_2=5\Omega R2=5Ω, R 3 = 2 Ω R_3=2\Omega R3=2Ω, R 4 = 10 Ω R_4=10\Omega R4=10Ω。

在该电路中,我们已经完成了步骤 1 和 2,Node3 已被选为电路的参考(地),并用接地符号表示。
根据步骤 3,我们可以将每个电流 I 1 I_1 I1、 I 2 I_2 I2、…、 I 5 I_5 I5 写为 V 12 V_{12} V12 和 V 13 V_{13} V13 的函数,通过将欧姆定律应用于每个分支来计算电流:
- I 1 = ( 10 − V 13 ) / R 1 I_1=(10-V_{13})/R_1 I1=(10−V13)/R1
- I 2 = V 13 / R 2 I_2=V_{13}/R_2 I2=V13/R2
- I 3 = ( V 13 − V 23 ) / R 3 I_3=(V_{13}-V_{23})/R_3 I3=(V13−V23)/R3
- I 4 = V 23 / R 4 I_4=V_{23}/R_4 I4=V23/R4
- I 5 = − S 2 = − 2 A I_5=-S_2=-2A I5=−S2=−2A
根据步骤4,我们在Node1和Node2处写出基尔霍夫电流定律:
- Node1: I 1 − I 2 − I 3 = 0 ⇒ [ ( 10 − V 13 ) / R 1 ] − [ V 13 / R 2 ] − [ ( V 13 − V 23 ) / R 3 ] = 0 I_1-I_2-I_3=0⇒[(10-V_{13})/R_1]-[V_{13}/R_2]-[(V_{13}-V_{23})/R_3]=0 I1−I2−I3=0⇒[(10−V13)/R1]−[V13/R2]−[(V13−V23)/R3]=0
- Node 2: I 3 − I 4 − I 5 = 0 ⇒ [ ( V 13 − V 23 ) / R 3 ] − [ V 23 / R 4 ] + S 2 = 0 I_3-I_4-I_5=0 ⇒ [(V_{13}-V_{23})/R_3]-[V_{23}/R_4]+S_2=0 I3−I4−I5=0⇒[(V13−V23)/R3]−[V23/R4]+S2=0
因此,我们获得了具有 2 个未知参数的 2 个方程的线性系统,可以通过将直线与适当的因子相乘、排列项并用其值替换电阻器和源项来更清晰地重写该方程:

该系统可以重写为矩阵方程:

这种类型的方程可以很容易地用手或使用MatLab等计算机程序求解,解为 V 13 = 9.1 V V_{13}=9.1V V13=9.1V和 V 23 = 10.1 V V_{23}=10.1V V23=10.1V。
由于每个电流都是这些值的函数,我们可以计算并列出它们:
- I 1 = ( 10 − 9.1 ) / 1 = 0.9 A I_1=(10-9.1)/1=0.9A I1=(10−9.1)/1=0.9A
- I 2 = 9.1 / 5 = 1.8 A I_2=9.1/5=1.8A I2=9.1/5=1.8A
- I 3 = ( 9.1 − 10.1 ) / 2 = − 0.5 A I_3=(9.1-10.1)/2=-0.5A I3=(9.1−10.1)/2=−0.5A
- I 4 = 10.1 / 10 = 1 A I_4=10.1/10=1A I4=10.1/10=1A
- I 5 = − 2 A I_5=-2A I5=−2A
2、网格电流分析
2.1 概述
本节介绍了另一种简化基尔霍夫电路定律 的强大方法,例如节点电压分析,称为网状电流分析 (MCA)。 我们没有像之前的方法那样将分析集中在节点周围,而是标记了电路每个网格中循环的电流。 网格仅由一个循环组成,其中没有其他内部循环。
我们在下面列出了执行网格电流分析的以下步骤:
- 1)电路每个网格上的属性和标签电流。 通常,我们选择顺时针方向为正电流。
- 2)对与前面所述的电流方向相同的每个网格应用基尔霍夫电压定律 (KVL)。
- 3)求解基尔霍夫电压定律分析中出现的循环方程。
- 4)根据网格电流计算电路中所需的电流或电压。
2.2 示例
假设图 2 中所示的电路,我们将对其执行网格电流分析。 给出不同元件的值: S 1 = 12 V S_1=12V S1=12V, S 2 = 6 V S_2=6V S2=6V; R 1 = 15 Ω R_1=15\Omega R1=15Ω, R 2 = 2 Ω R_2=2\Omega R2=2Ω, R 3 = 12 Ω R_3=12\Omega R3=12Ω。

电路中已经完成第一步,其中网格电流用红色环路符号标记。
正如步骤 2 所示,我们对电路的每个网格应用基尔霍夫电压定律:
- 方程1: − V 1 + I 1 × ( R 1 + R 2 ) − I 2 × R 2 = 0 -V_1+I_1×(R_1+R_2)-I_2×R_2=0 −V1+I1×(R1+R2)−I2×R2=0
- 方程2: V 2 − I 1 × R 2 + I 2 × ( R 2 + R 3 ) = 0 V_2-I_1×R_2+I_2×(R_2+R_3)=0 V2−I1×R2+I2×(R2+R3)=0
在我们的例子中,网格电流 I 1 I_1 I1 和 I 2 I_2 I2 都存在于电阻器 R 2 R_2 R2 上,在两个方程中我们可以看到 R 2 R_2 R2 上的电流被视为 I 1 I_1 I1 和 I 2 I_2 I2 的代数和。
下面,我们用参数值替换参数,首先,根据第一个方程,我们将 I 1 I_1 I1 表示为 I 2 I_2 I2 的函数:
- I 1 = ( 12 + 2 × I 2 ) / 17 I_1=(12+2×I_2)/17 I1=(12+2×I2)/17
我们将此项代入方程 2,重新分配各项后,可得出 I 2 = − 1 / 3 A I_2=-1/3A I2=−1/3A。我们将此值代入 I 1 I_1 I1 的表达式中,可得出 I 1 = 2 / 3 A I_1=2/3 A I1=2/3A。
最后,我们可以给出驱动电路所需的电流 I I = I 1 − I 2 = 1 A II=I_1-I_2=1A II=I1−I2=1A。
3、总结
- 我们在本文中介绍了两种基于基尔霍夫电路定律的方法,称为节点电压分析 (NVA) 和网格电流分析 (MCA)。 这些方法可以更有效地分析电路,因为它们通过减少涉及的数学量,比 基于基尔霍夫定律更快地得出解决方案。
- 每个分析都包含一系列要执行的步骤,这些方法在各自部分的开头单独介绍。
- 另外,还给出了示例以说明如何使用这两种方法分析电阻电路。 我们可以注意到,对于具有电感器和电容器的电抗电路,NVA 或 MCA 分析会导致需要求解微分方程或微分方程组。
相关文章:

【电路笔记】-节点电压分析和网状电流分析
节点电压分析和网状电流分析 文章目录 节点电压分析和网状电流分析1、节点电压分析1.1 概述1.2 示例 2、网格电流分析2.1 概述2.2 示例 3、总结 正如我们在上一篇介绍电路分析基本定律的文章中所看到的,基尔霍夫电路定律 (KCL) 是计算任何电路中未知电压和电流的强大…...
jenkins通知
构建失败邮件通知 配置自己的邮箱 配置邮件服务,密码是授权码 添加构建后操作 扩展 配置流水线 添加扩展 钉钉通知 Jenkins安装钉钉插件 钉钉添加机器人 加签 https://oapi.dingtalk.com/robot/send?access_token98437f84ffb6cd64fa2d7698ef44191d49a11…...

技术分享 | Spring Boot 异常处理
Java 异常类 首先让我们简单了解或重新学习下 Java 的异常机制。 Java 内部的异常类 Throwable 包括了 Exception 和 Error 两大类,所有的异常类都是 Object 对象。 Error 是不可捕捉的异常,通俗的说就是由于 Java 内部 JVM 引起的不可预见的异常&#…...

【Python 千题 —— 基础篇】成绩评级
题目描述 题目描述 期末考试结束,请根据同学的分数为该同学评级。 A:90 ~ 100B:80 ~ 89C:70 ~ 79D:60 ~ 69E:0 ~ 60 输入描述 输入同学的分数。 输出描述 输出该同学的等级。 示例 示例 ① 输入&…...

【ARM Coresight OpenOCD 系列 2 -- OpenOCD 脚本语法详细介绍】
请阅读【ARM Coresight SoC-400/SoC-600 专栏导读】 文章目录 1.1 swj-dp.tcl 介绍1.1.1 source [find target/swj-dp.tcl]1.1.2 调试传输协议选择 transport selec1.1.3 newtap 命令介绍1.1.4 内存读取数据函数 mem2array1.1.5 变量名检查1.1.6 设置 flash 烧录用到的 ram 空…...

pytorch 初始化
初始化 import matplotlib.pyplot as plt import torch import torch.nn as nn from torch.utils.data import Dataset,DataLoader import torch.optim as optim import numpy as np random_seed=1000 # np.random.seed(random_seed) torch.manual_seed(random_seed)#自定义损…...

process.env.XXX环境变量不生效的解决方法
问题: 使用process.env.XXX时获取不到环境变量的值: axios.defaults.baseURL process.env.VUE_APP_BASE_API; 解决方法: 一:.env.development和.env.production 必须在根目录下。 二:项目根目录下的.env.develop…...

QT项目|时间服务器架构
目录 一、 创建新UI界面的标题 二、 创建服务器运行图标 2.1 查找图标,并截图 2.2 加入QT资源库 三、编辑UI界面 3.1 根据要求,绘制UI界面 3.2 对控件进行命名 3.3 加入Group Box进行美化 四、 按钮操作设置 4.1 QT加入网络 4.2 转到槽&…...
Java学习 10.Java-数组习题
一、创建一个 int 类型的数组, 元素个数为 100, 并把每个元素依次设置为 1 - 100 代码实现 public static void main(String[] args) {int[] arrnew int[100];for (int i 0; i < arr.length; i) {arr[i]i1;}System.out.println(Arrays.toString(arr));} 运行结果 二、改变…...

Vue3使用vue-print-nb插件打印功能
插件官网地址https://www.npmjs.com/package/vue-print-nb 效果展示: 打印效果 根据不同的Vue版本安装插件 //Vue2.0版本安装方法 npm install vue-print-nb --save pnpm install vue-print-nb --save yarn add vue-print-nb//Vue3.0版本安装方法: npm install vue3…...

Leetcode300 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 示例 1…...
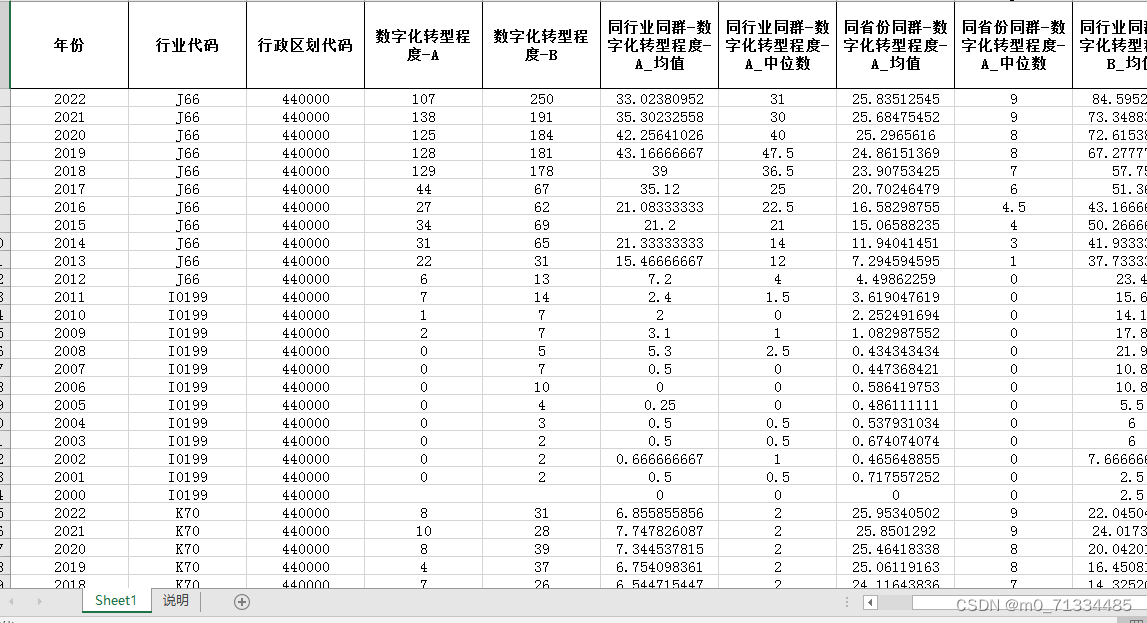
2000-2022年上市公司数字化转型同群效应数据
2000-2022年上市公司数字化转型同群效应数据 1、时间:2000-2022年 2、指标:股票代码、年份、行业代码、行政区划代码、数字化转型程度-A、数字化转型程度-B、同行业同群-数字化转型程度-A_均值、同行业同群-数字化转型程度-A_中位数、同省份同群-数字化…...
 对象创建型设计模式?)
Python 如何实践 Builder(生成器) 对象创建型设计模式?
开始之前,我们先介绍一下该模型的基本信息。 生成器(Builder)设计模式是一种创建型设计模式,它用于创建复杂对象,将对象的构建过程与表示分离。这种分离可以让我们创建不同类型或配置的对象,同时避免构造函…...
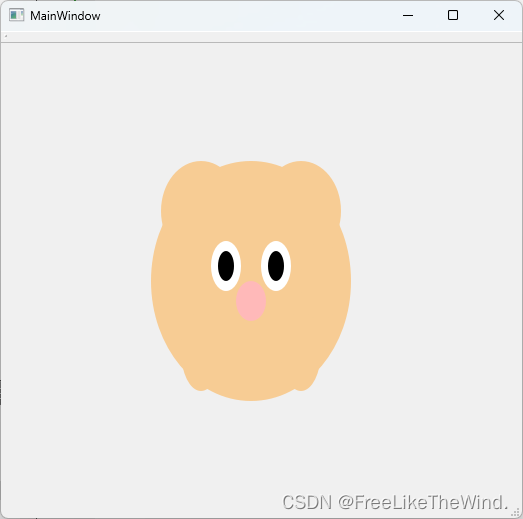
【Qt绘制小猪】以建造者模式绘制小猪
效果 学以致用,使用设计模式之建造者模式绘制小猪。 代码 接口:申明绘制的步骤 PigBuilder.h #ifndef PIGBUILDER_H #define PIGBUILDER_H#include <QObject> #include <QPainter>class PigBuilder : public QObject {Q_OBJECT public:ex…...

开发中常用的SQL语句
开发中常用的SQL语句 1.update更新时不能引用本身表2.备份MySQL3.函数的使用1. case,when的使用2. IF3.其它4.拼接5. 处理时间 4.导出表结构注释等 1.update更新时不能引用本身表 UPDATE student SET valid_flag 0 WHERE id IN (SELECT idFROM (SELECT su.idFROM student su …...
Unreal UnLua + Lua Protobuf
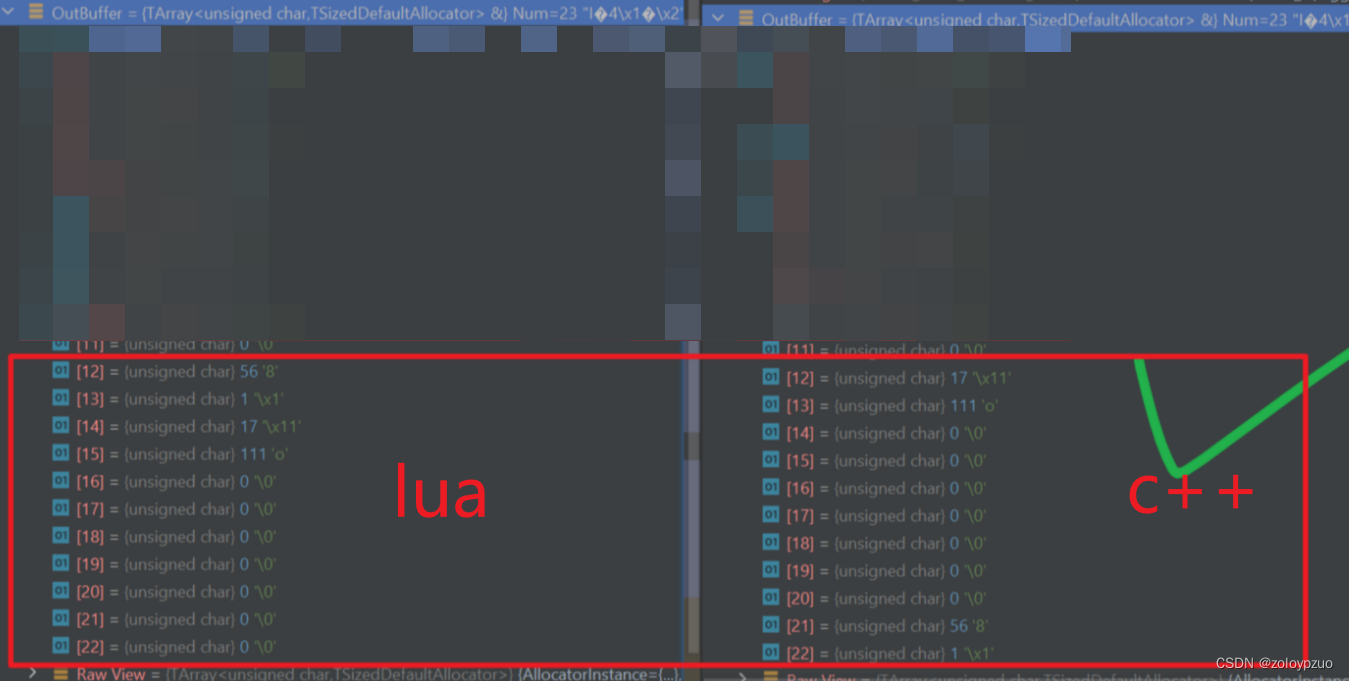
Unreal UnLua Lua Protobuf https://protobuf.dev/ protobuf wire format:pb 编译到底层的数据协议 https://github.com/starwing/lua-protobuf/blob/master/README.zh.md buffer 处理 lua string 可以当 buffer 用,# len 不会遇到 0 截断…...

java 类和对象 (图文搭配,万字详解!!)
关于java类和对象,我们要掌握几个重点! 1.类的定义方式以及对象的实例化 2.类中的成员变量和成员方法的使用 3.对象的整个初始化过程 4.封装特性 5.代码块 目录 一、面向对象的初步认识 1.1 什么是面向对象 1.2 面向对象与面向过程 1.2.1传统洗…...

pytorch DistributedDataParallel 分布式训练踩坑记录
目录 一、几个比较常见的概念:二、踩坑记录2.1 dist.init_process_group初始化2.2 spawn启动(rank怎么来的)2.3 loss backward2.4 model cuda设置2.5 数据加载 一、几个比较常见的概念: rank: 多机多卡时代表某一台机器ÿ…...
Stable Diffusion webui 源码调试(三)
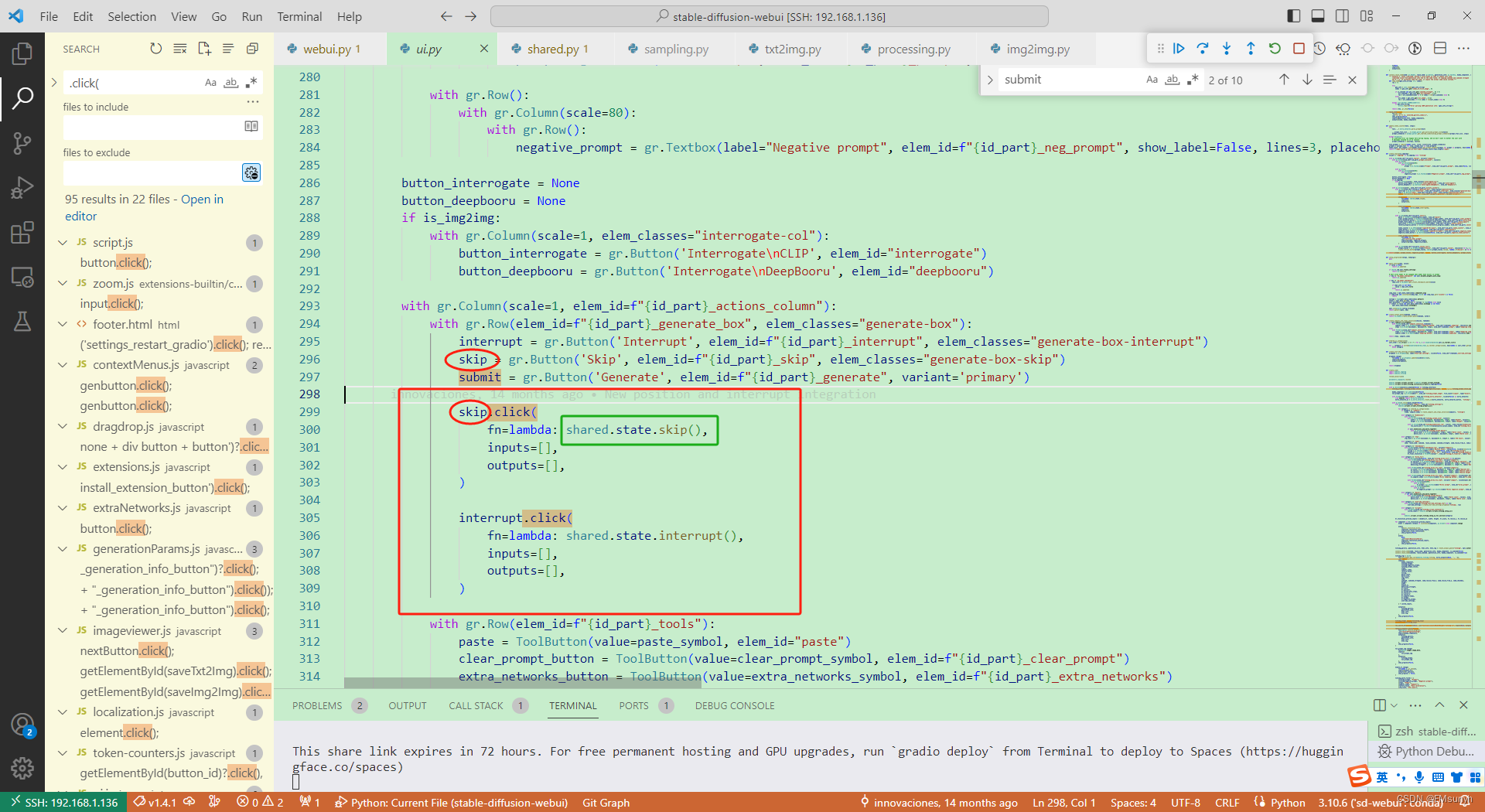
Stable Diffusion webui 源码调试(三) 个人模型主页:LibLibai stable-diffusion-webui 版本:v1.4.1 内容更新随机,看心情调试代码~ shared 变量 shared变量,简直是一锅大杂烩,shared变量存放…...

工作学习记录
1、Spring的Lifecycle和SmartLifecycle Spring的Lifecycle和SmartLifecycle,可以没用过,但不能不知道!-CSDN博客 2、Shiro安全框架提供了认证、授权、企业会话管理、加密、缓存管理相关的功能,使用Shiro可以非常方便的完成项目的…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
