NO.304 二维区域和检索 - 矩阵不可变
题目
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。
思路
思路一
该题目可以作为一维前缀和的扩展(参见Leecode-303)。
初始化时对矩阵的每一行计算前缀和,检索时对二维区域中的每一行计算子数组和,然后对每一行的子数组和计算总和。
时间复杂度:初始化 O(mn),每次检索 O(m),其中 m 和 n 分别是矩阵 matrix的行数和列数。初始化需要遍历矩阵 matrix计算二维前缀和,时间复杂度是 O(mn)。 每次检索需要对二维区域中的每一行计算子数组和,二维区域的行数不超过 m,计算每一行的子数组和的时间复杂度是 O(1),因此每次检索的时间复杂度是 O(m)。
空间复杂度:O(mn),其中 m 和 n 分别是矩阵 matrix的行数和列数。需要创建一个 m行 n+1 列的前缀和数组 sums。
思路二
小学数学,田字形,已知整体面积,上面面积,左边面积,左上面积,求右下角矩形的面积。 右下角矩形的面积=整体面积-上面面积-左边面积+左上面积
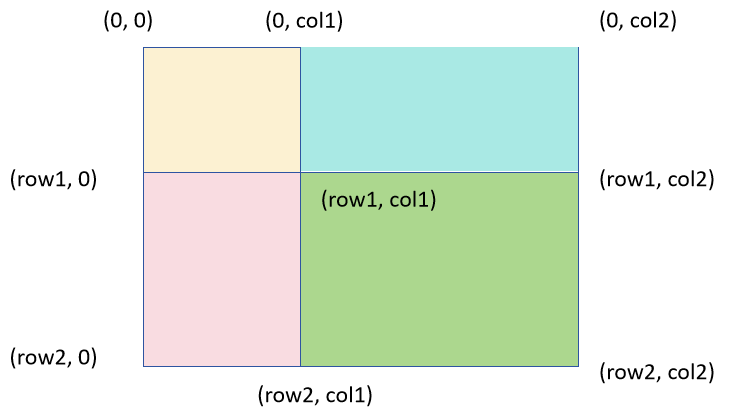
根据上述描述,假设我们计算(row1, col1),(row2, col2)之间的值,可以使用以下的公式:
我们在初始化的时候,可以计算每一个点对应的面积值
时间复杂度:初始化 O(mn),每次检索 O(1),其中 m 和 n 分别是矩阵 matrix的行数和列数。 初始化需要遍历矩阵 matrix 计算二维前缀和,时间复杂度是 O(mn)。 每次检索的时间复杂度是 O(1)。
空间复杂度:O(mn),其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个 m+1 行 n+1 列的二维前缀和数组 sums。
代码
class NumMatrix {int[][] sums;public NumMatrix(int[][] matrix) {int m = matrix.length;if (m > 0) {int n = matrix[0].length;sums = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];}}}}public int sumRegion(int row1, int col1, int row2, int col2) {return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];}
}
相关文章:
NO.304 二维区域和检索 - 矩阵不可变
题目 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。 实现 NumMatrix 类: NumMatrix(int[][] matrix) 给定整数矩阵 …...

牛客---简单密码python
现在有一种密码变换算法。 九键手机键盘上的数字与字母的对应: 1--1, abc--2, def--3, ghi--4, jkl--5, mno--6, pqrs--7, tuv--8 wxyz--9, 0--0,把密码中出现的小写字母都变成九键键盘对应的数字,如:a 变成 2&#x…...
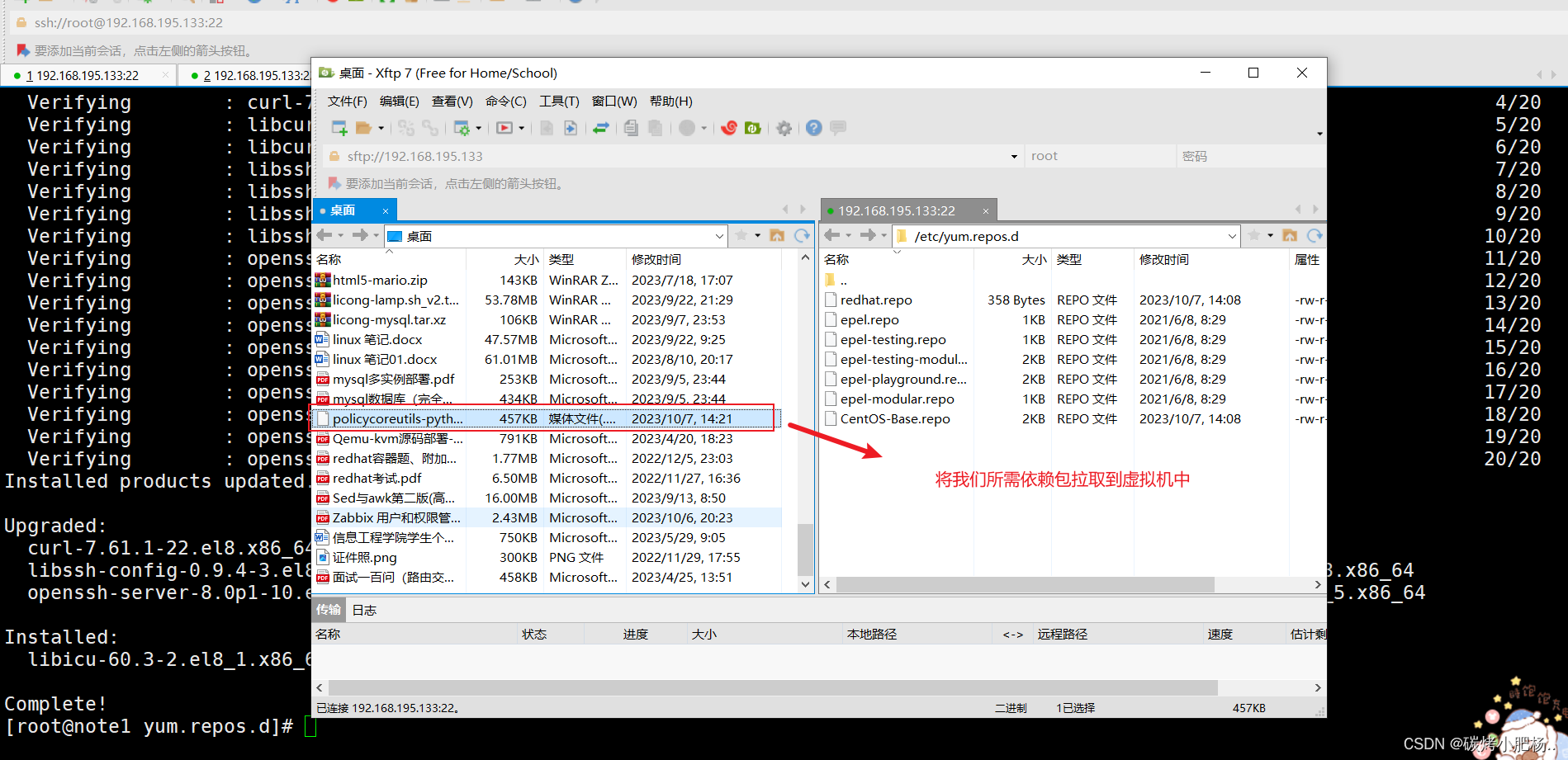
devops完整搭建教程(gitlab、jenkins、harbor、docker)
devops完整搭建教程(gitlab、jenkins、harbor、docker) 文章目录 devops完整搭建教程(gitlab、jenkins、harbor、docker)1.简介:2.工作流程:3.优缺点4.环境说明5.部署前准备工作5.1.所有主机永久关闭防火墙…...

页面上时间显示为数字 后端返回给前端 response java系统
有时候,在一个系统里,会看到,有的页面时间显示正常,有的页面时间显示成数字。像这样: "createTime": 1698706491000 这是因为出参没有做转换,直接将java.util.Date类型的数据返回给前端了。 返…...

idea怎么配置tomcat
要在IntelliJ IDEA中配置Tomcat,请按照以下步骤操作: 打开IntelliJ IDEA,点击File -> Settings(或者使用快捷键CtrlAltS)。 在设置窗口左侧导航栏中,选择Build, Execution, Deployment -> Applicati…...
GoLong的学习之路(二十三)进阶,语法之并发(go最重要的特点)(锁,sync包,原子操作)
这章是我并发系列中最后的一章。这章主要讲的是锁。但是也会讲上一章channl遗留下的一些没有讲到的内容。select关键字的用法,以及错误的一些channl用法。废话不多说。。。 文章目录 select多路复用通道错误示例并发安全和锁问题描述互斥锁读写互斥锁 syncsync.Wait…...

asp.net core 生命周期
在ASP.NET Core中,有三个重要的生命周期阶段: 请求生命周期(Request Lifecycle):请求生命周期从接收到客户端的HTTP请求开始,到响应结果发送给客户端结束。在请求生命周期中,ASP.NET Core会创建…...
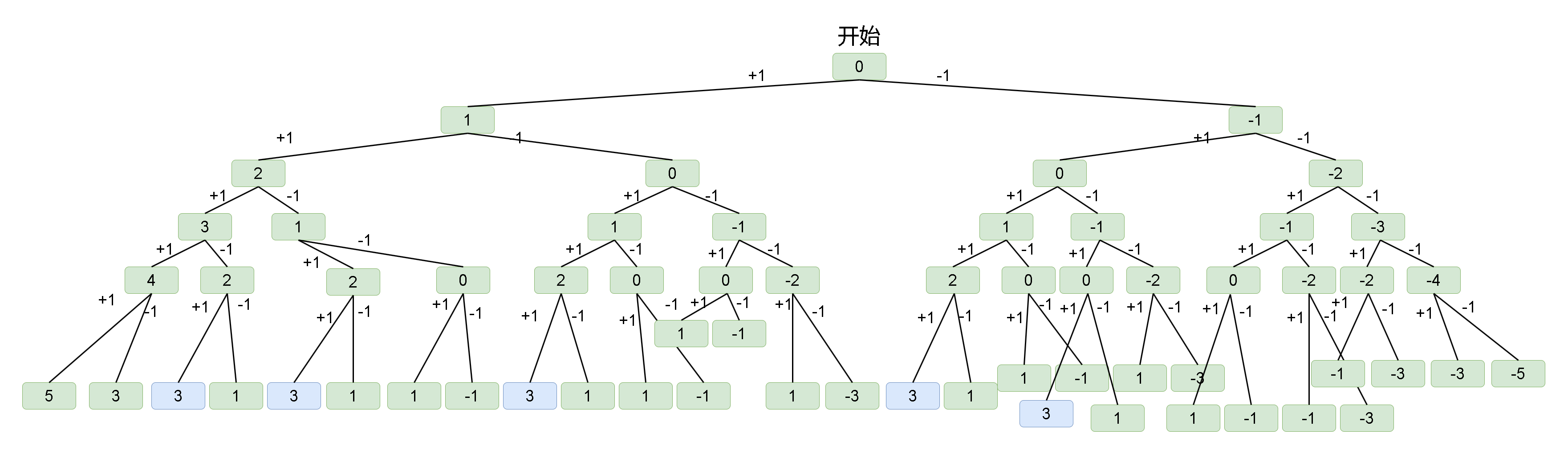
Leetcode刷题详解—— 目标和
1. 题目链接:494. 目标和 2. 题目描述: 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可…...

学习c#的第六天
目录 C# 判断 if 语句 嵌套 if 语句 switch 语句 嵌套 switch 语句 ? : 运算符 C# 循环 循环类型 while 循环 for/foreach 循环 do...while 循环 嵌套循环 循环控制语句 break 语句 continue 语句 无限循环 C# 判断 if 语句 在C#中,if语句用于根…...

第七章 :Spring Boot web开发常用注解(二)
第七章 :Spring Boot web开发常用注解(二) 前言 本章节知识重点:作者结合自身开发经验,以及觉察到的一个现象:Springboot注解全面理解和掌握的并不多,对注解进行了全面总结,共分两个章节,可以作为web开发工程师注解参考手册,SpringBoot常用注解大全,一目了然!。本…...
IOC - Google Guice
Google Guice是一个轻量级的依赖注入框架,专注于依赖注入和IoC,适用于中小型应用。 Spring Framework是一个全面的企业级框架,提供了广泛的功能,适用于大型企业应用。 是吧!IOC 容器不止Spring,还有Google Guice,来体…...

国际阿里云:Linux实例负载高问题排查和异常处理!!!
问题描述 在您使用ECS实例过程中,可能会遇到实例系统负载较高的情况,负载过高,可能会引发一系列异常问题,简单说您如下: CPU使用率或负载过高:一般来说,当CPU使用率≥80%时,定义为C…...
【数据结构】二叉树的遍历递归算法详解
二叉树的遍历 💫二叉树的结点结构定义💫创建一个二叉树结点💫在主函数中手动创建一颗二叉树💫二叉树的前序遍历💫调用栈递归——实现前序遍历💫递归实现中序和后序遍历 💫二叉树的结点结构定义 …...

百度王颖:百度文库以AI创作能力突破语言边界,促进思想碰撞和文化融通
1月9日,2023年世界互联网大会乌镇峰会“网络传播与文明交流互鉴论坛”召开。百度副总裁、互娱和垂类平台负责人王颖出席并发表“以技术搭建跨文化交流桥梁”主题演讲。她表示,在大模型的加持下,百度各个产品都在重构,通过技术助力…...

人工智能基础_机器学习023_理解套索回归_认识L1正则---人工智能工作笔记0063
然后上一节我们说了L1,L2正则是为了提高,模型的泛化能力, 提高泛化能力,实际上就是把模型的公式的w,权重值,变小对吧. 然后我们这里首先看第一个L1正则,是怎么做到把w权重变小的 可以看到最上面是线性回归的损失函数,然后 L1可以看到,这个正则,就是在损失函数的基础上给损失…...

Learning an Animatable Detailed 3D Face Model from In-The-Wild Images论文笔记
Learning an Animatable Detailed 3D Face Model from In-The-Wild Images论文笔记 论文目标:提出一个端到端的框架,可以从非受控的图片中学习高质量、可动画的3D人脸模型。论文方法:论文结果:论文意义: 论文目标:提出一个端到端的框架,可以从非受控的图片中学习高质量、可动画…...

Lenovo联想小新Air-14笔记本2021款AMD锐龙ALC版(82LM)原装出厂Win10镜像和Windows11预装OEM系统
下载链接:https://pan.baidu.com/s/1akLkXM2HIg3eO76jqM-LVA?pwdxvo6 提取码:xvo6 系统自带所有驱动、出厂主题壁纸、系统属性专属LOGO标志、Office办公软件、联想电脑管家等预装程序 所需要工具:16G或以上的U盘 文件格式:…...
在程序中链接静态库
现在我们把上面src目录中的add.cpp、div.cpp、mult.cpp、sub.cpp编译成一个静态库文件libcalc.a。 add_library(库名称 STATIC 源文件1 [源文件2] ...) link_libraries(<static lib> [<static lib>...]) 参数1:指定出要链接的静态库的名字 可以是全…...
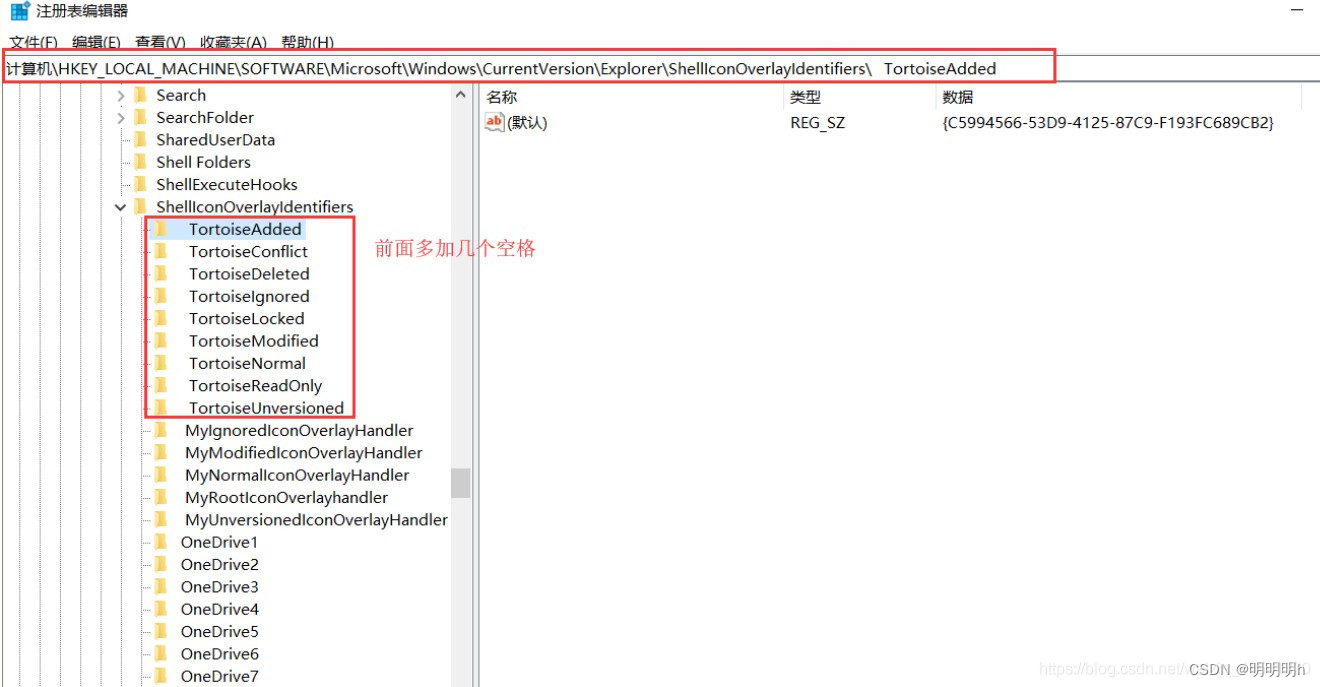
TortoiseSVN 状态图标不显示的两种解决办法
文章目录 TortoiseSVN 方式解决注册表方式解决 TortoiseSVN 方式解决 在桌面或者资源管理器中鼠标右键打开 TortoiseSVN 设置选择 Icon Overlays (图标覆盖)Status cache(状态缓存) 选择 ‘Shell’ 选择 Icon Overlays(图标覆盖)…...
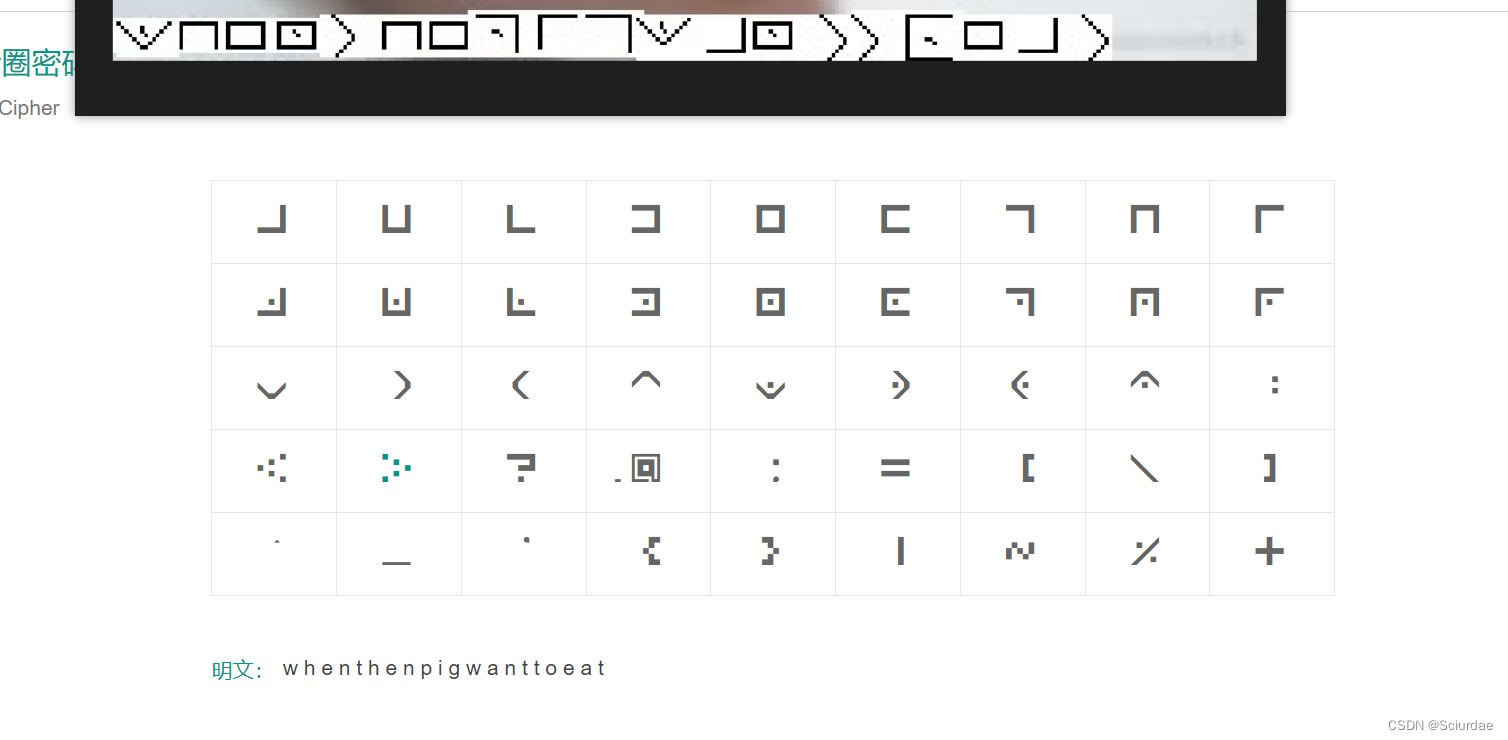
NSSCTF-Crypto入门题 练习记录贴 ‘‘一‘‘
文章目录 前言001[鹤城杯 2021]easy_crypto002[强网拟态 2021]拟态签到题003[SWPUCTF 2021 新生赛]crypto8004[SWPUCTF 2021 新生赛]crypto7005[SWPUCTF 2021 新生赛]crypto6006[SWPUCTF 2021 新生赛]ez_caesar007[SWPUCTF 2021 新生赛]crypto10008[鹤城杯 2021]A_CRYPTO009[SW…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
