【数据结构】二叉树的遍历递归算法详解
二叉树的遍历
- 💫二叉树的结点结构定义
- 💫创建一个二叉树结点
- 💫在主函数中手动创建一颗二叉树
- 💫二叉树的前序遍历
- 💫调用栈递归——实现前序遍历
- 💫递归实现中序和后序遍历
💫二叉树的结点结构定义
typedef struct BinaryTreeNode
{int val;struct BinaryNode* left;struct BinaryNode* right;
}BTNode;
💫创建一个二叉树结点
我们来写一个函数BuyNode(x)函数用于创建二叉树结点。
用动态开辟函数malloc函数进行动态开辟,并强制转换为BTNode型,用变量node来去管理开辟的空间。
我们初始化结点,其val即为传入的参数x,左右指针left和right都设为NULL。
//创建一个二叉树结点
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");}else{node->val = x;node->left = NULL;node->right = NULL;}
}
💫在主函数中手动创建一颗二叉树
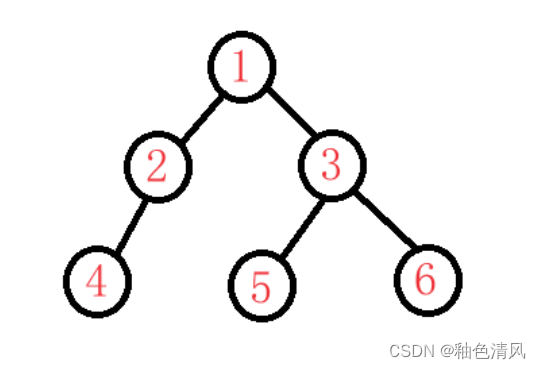
我们在主函数中创建上面这样一颗二叉树。
首先,我们需要开辟6个结点,但此时6个结点之间没有任何的联系,我们需要改变其中一些结点的指针域left和right,来使得结点之间产生联系。
int main()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node1->right=node3;node2->left = node4;node3->left = node5;node3->right = node6;return 0;
}
💫二叉树的前序遍历
首先,我们先要了解以下二叉树前序的前序遍历。
二叉树的前序遍历:
根-->左子树-->右子树
对于我们上面的这颗二叉树:

1-->左-->右
左子树和右子树也采用前序遍历的方式:

左子树:
2-->4
右子树
3-->5-->6
所以这颗二叉树的前序遍历为:
1-->2-->4-->3-->5-->6
正是由于这样的思想,将一个树根-->左-->右的左和右仍然是一颗树,接着再拆分…直到左子树和右子树的左右结点为空时。
所以这样的思想,我们就利用递归的想法就可以完成一颗二叉树的遍历。
💫调用栈递归——实现前序遍历
调用栈:程序在执行时,如果程序调用一个函数,它会先把这个函数压入栈中,等到这个函数返回结果(return )后,它才会从栈中弹出。
递归程序在执行时,会不断地调用自身,把函数压入栈中,当最后一个函数,也就是基线条件出现时,再逐渐清空栈空间。
下面我们根据这段代码来画图理解一些递归的思想。
//递归前序遍历一棵树
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}printf("%d", root->val);PreOrder(root->left);PreOrder(root->right);return 0;
}

我们按照步骤来执行以下程序:
①主函数中进行了函数调用,参数为node1
压栈:

node1不为空,打印结点:

②执行PreOrder(root->left),再次调用函数,参数为node2
进行压栈:
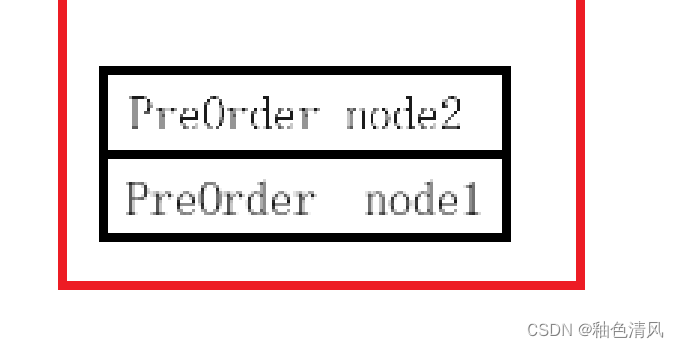
node2不为空,打印

③执行PreOrder(root->left),再次调用函数,参数为node4,压栈:
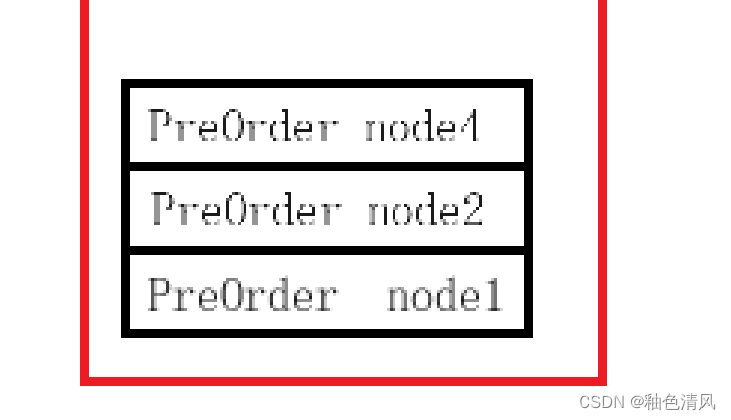
node4不为空,打印:
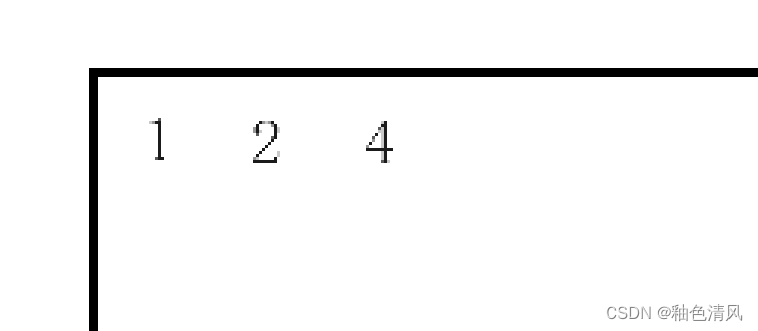
④执行PreOrder(root->left),再次调用函数,参数为NULL,压栈:
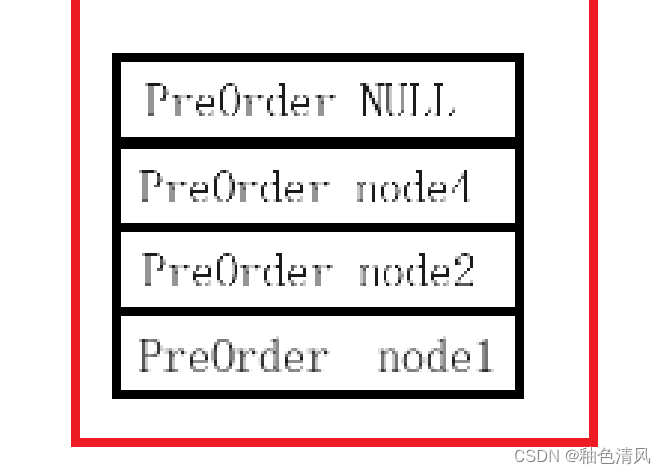
这是函数参数为NULL,进入if语句,进行打印 ,并return返回,这时出栈。

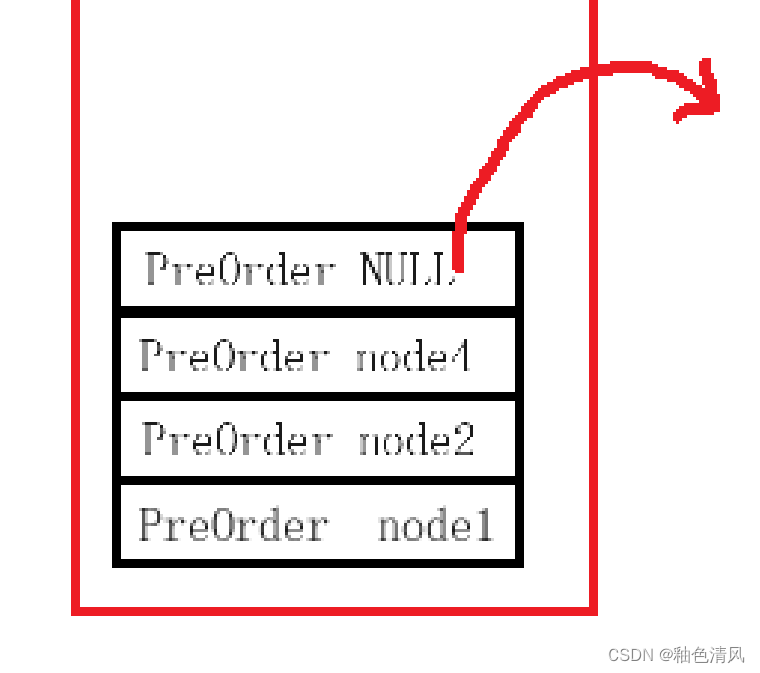

⑤y由于这段代码,当函数的参数为node4时,PreOrder(node4->left)已经有return,所以这时,程序会接着往下面执行PreOrder(node4->right)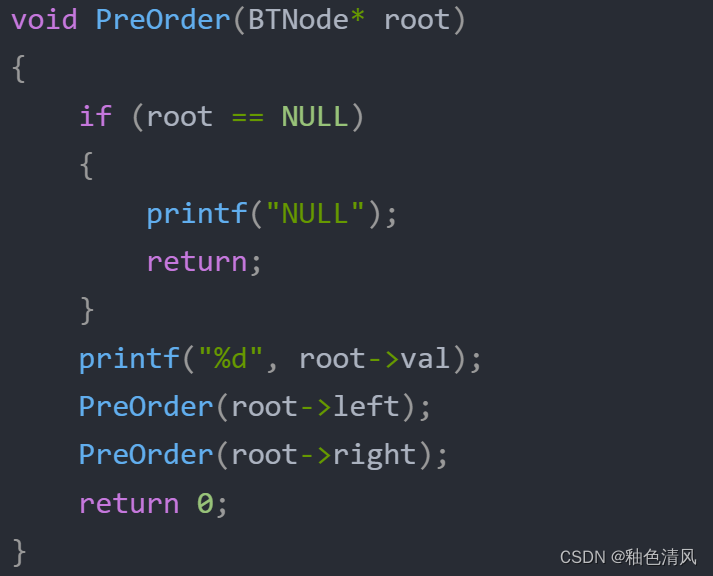
这时再次调用函数,函数参数为NULL,压栈,打印,再出栈。



⑥ 这时对于函数PreOrder (node4)已经执行完语句 PreOrder(node4->left)和语句PreOrder(node4->right)了,后执行 return 0,函数有返回结果,所以出栈。
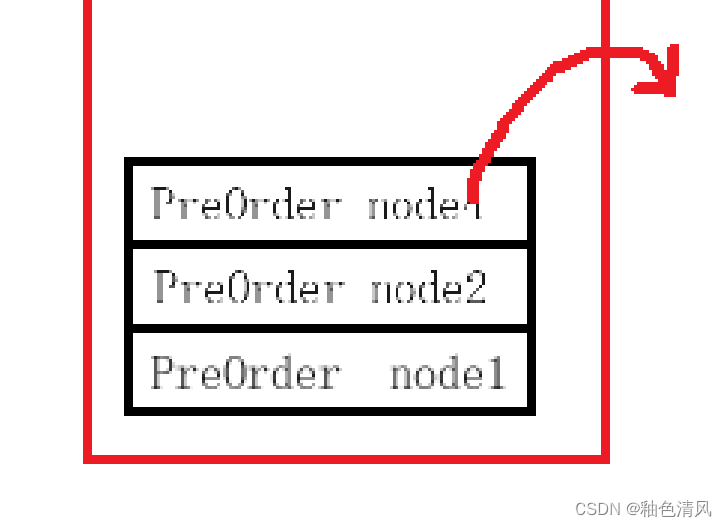

⑦此时,我们该执行 node2的右结点了。
对于PreOrder(node2->right)中,函数函数即是NULL,所以先压栈,然后打印,然后出栈。

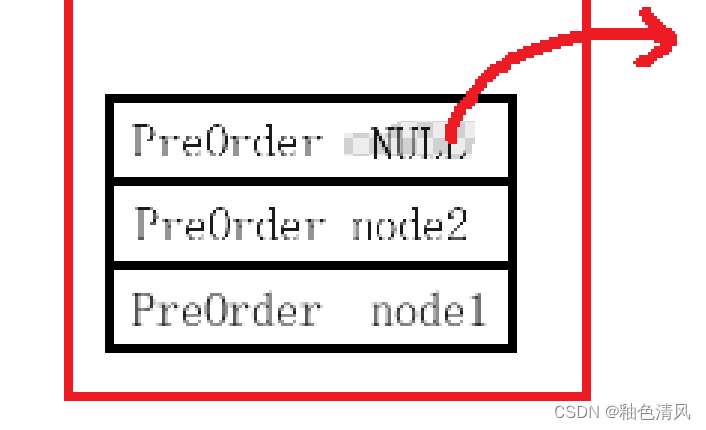


⑧此时,函数PreOrder(node2) 的PreOrder(node2->left) 和PreOrder(node2->right) 都已经执行完了,即已经对node2结点的左右子树遍历完成,执行return 0 返回,这时PreOrder(node2) 出栈。

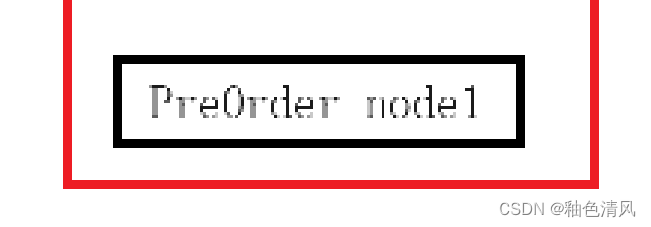
在此时,我们已经对node1的左子树遍历完成,接下来同遍历左子树一样,我们对右子树进行遍历。


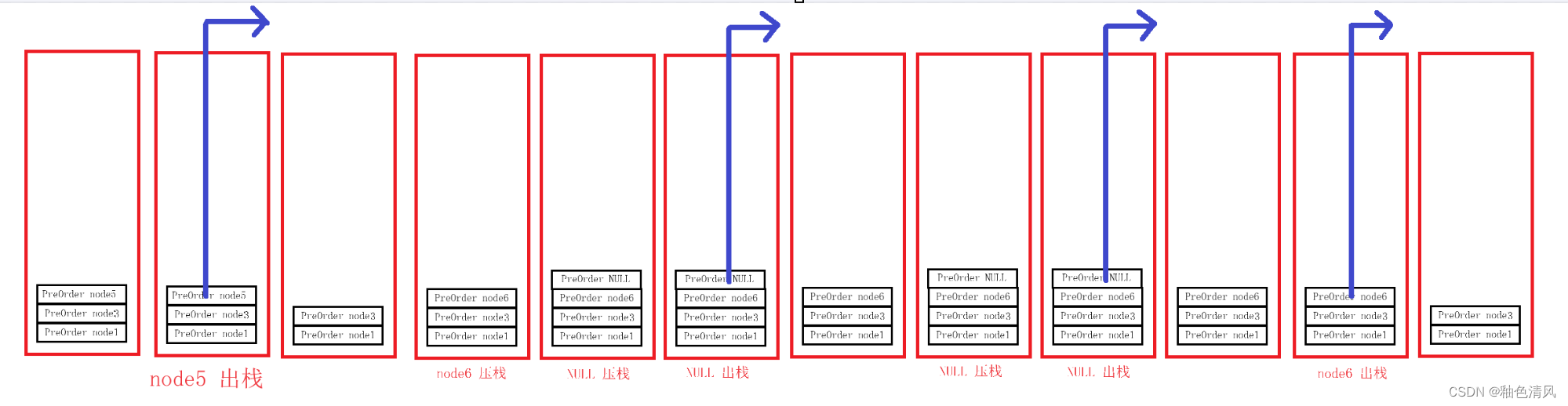

这时输出为:

💫递归实现中序和后序遍历
根据上面前序的递归,我觉得最重要的代码是:
if (root == NULL){printf("NULL");return;}
它是递归中能否回溯的一个关键。
下面写中序遍历:
//递归中序遍历二叉树
void Order(BTNode* root)
{if (root == NULL){printf("NULL ");return;}Order(root->left);printf("%d ", root->val);Order(root->right);return 0;
}
递归后序遍历一棵树:
//递归后序遍历一颗二叉树
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);return 0;
}
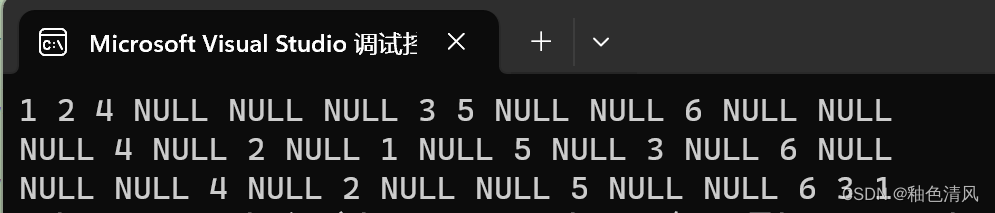
前中后序遍历结果分别为:
相关文章:

【数据结构】二叉树的遍历递归算法详解
二叉树的遍历 💫二叉树的结点结构定义💫创建一个二叉树结点💫在主函数中手动创建一颗二叉树💫二叉树的前序遍历💫调用栈递归——实现前序遍历💫递归实现中序和后序遍历 💫二叉树的结点结构定义 …...

百度王颖:百度文库以AI创作能力突破语言边界,促进思想碰撞和文化融通
1月9日,2023年世界互联网大会乌镇峰会“网络传播与文明交流互鉴论坛”召开。百度副总裁、互娱和垂类平台负责人王颖出席并发表“以技术搭建跨文化交流桥梁”主题演讲。她表示,在大模型的加持下,百度各个产品都在重构,通过技术助力…...

人工智能基础_机器学习023_理解套索回归_认识L1正则---人工智能工作笔记0063
然后上一节我们说了L1,L2正则是为了提高,模型的泛化能力, 提高泛化能力,实际上就是把模型的公式的w,权重值,变小对吧. 然后我们这里首先看第一个L1正则,是怎么做到把w权重变小的 可以看到最上面是线性回归的损失函数,然后 L1可以看到,这个正则,就是在损失函数的基础上给损失…...

Learning an Animatable Detailed 3D Face Model from In-The-Wild Images论文笔记
Learning an Animatable Detailed 3D Face Model from In-The-Wild Images论文笔记 论文目标:提出一个端到端的框架,可以从非受控的图片中学习高质量、可动画的3D人脸模型。论文方法:论文结果:论文意义: 论文目标:提出一个端到端的框架,可以从非受控的图片中学习高质量、可动画…...

Lenovo联想小新Air-14笔记本2021款AMD锐龙ALC版(82LM)原装出厂Win10镜像和Windows11预装OEM系统
下载链接:https://pan.baidu.com/s/1akLkXM2HIg3eO76jqM-LVA?pwdxvo6 提取码:xvo6 系统自带所有驱动、出厂主题壁纸、系统属性专属LOGO标志、Office办公软件、联想电脑管家等预装程序 所需要工具:16G或以上的U盘 文件格式:…...
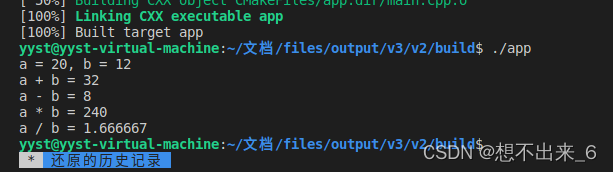
在程序中链接静态库
现在我们把上面src目录中的add.cpp、div.cpp、mult.cpp、sub.cpp编译成一个静态库文件libcalc.a。 add_library(库名称 STATIC 源文件1 [源文件2] ...) link_libraries(<static lib> [<static lib>...]) 参数1:指定出要链接的静态库的名字 可以是全…...
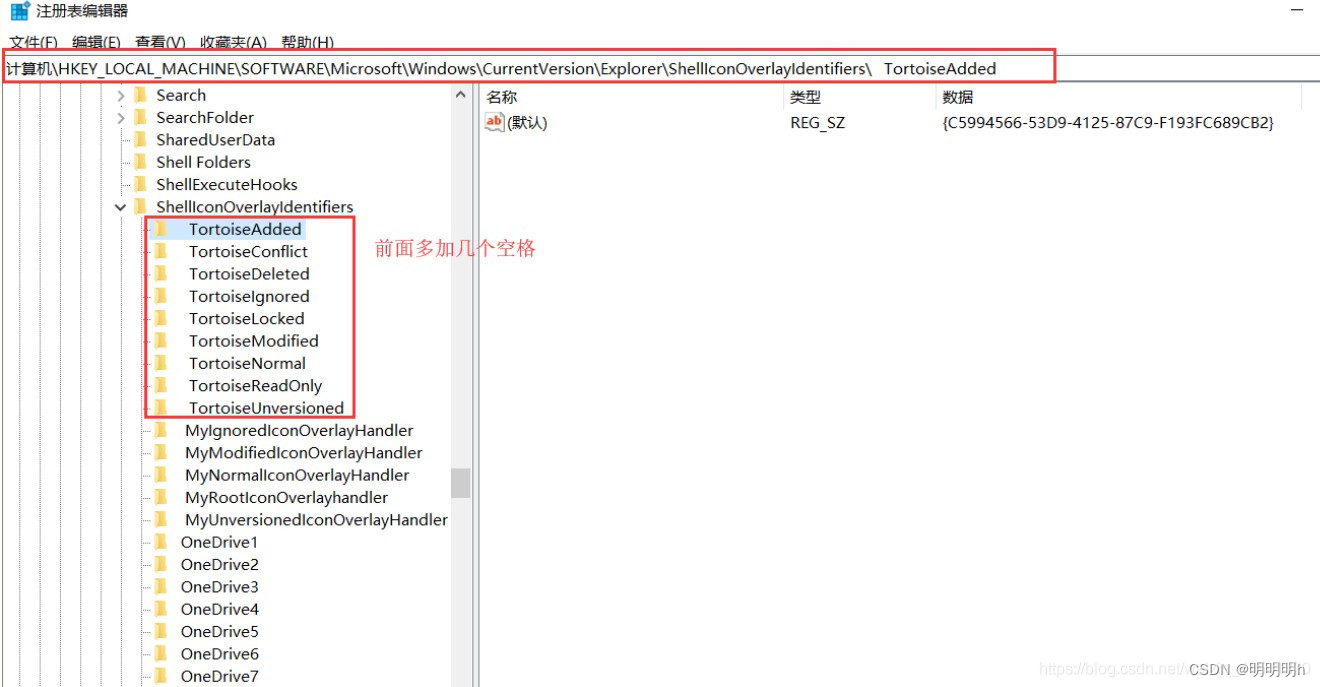
TortoiseSVN 状态图标不显示的两种解决办法
文章目录 TortoiseSVN 方式解决注册表方式解决 TortoiseSVN 方式解决 在桌面或者资源管理器中鼠标右键打开 TortoiseSVN 设置选择 Icon Overlays (图标覆盖)Status cache(状态缓存) 选择 ‘Shell’ 选择 Icon Overlays(图标覆盖)…...
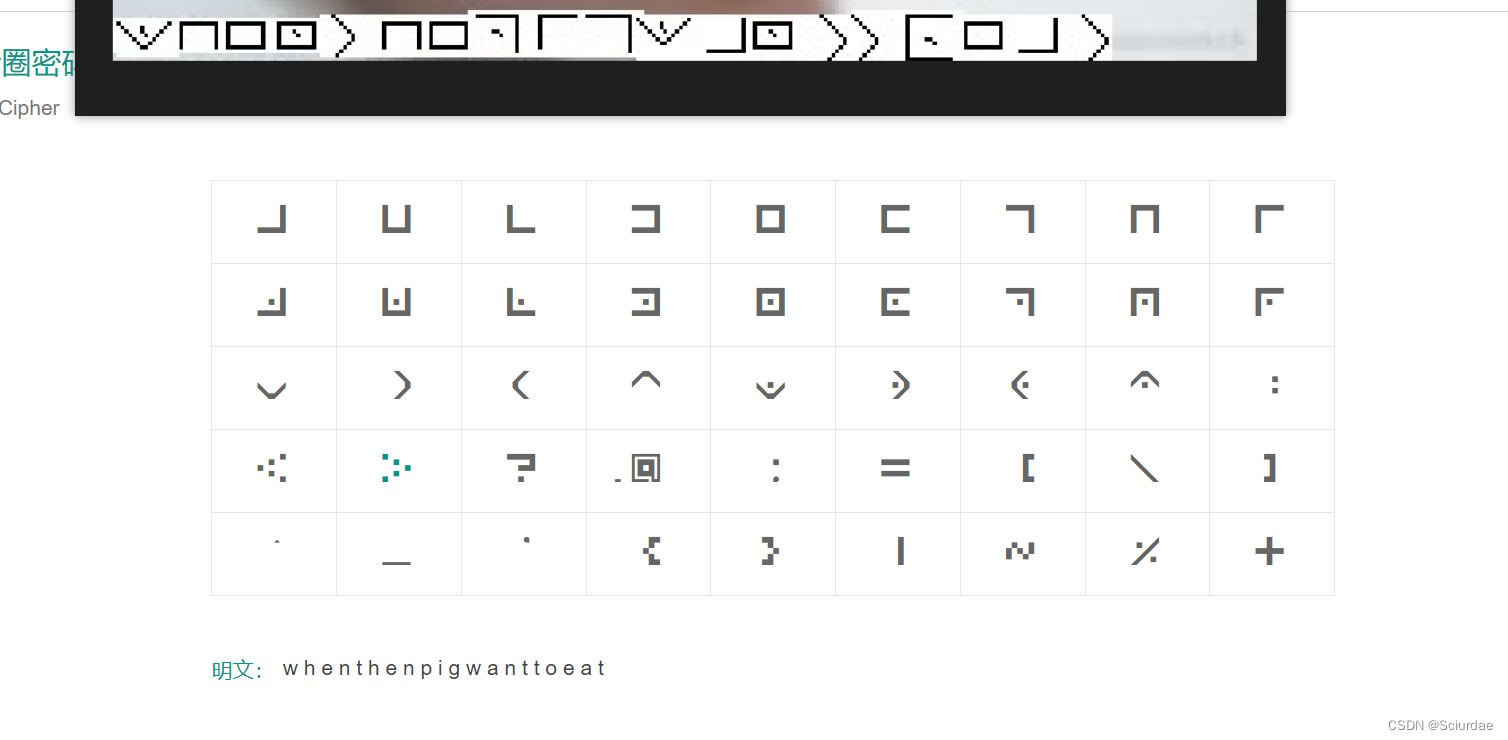
NSSCTF-Crypto入门题 练习记录贴 ‘‘一‘‘
文章目录 前言001[鹤城杯 2021]easy_crypto002[强网拟态 2021]拟态签到题003[SWPUCTF 2021 新生赛]crypto8004[SWPUCTF 2021 新生赛]crypto7005[SWPUCTF 2021 新生赛]crypto6006[SWPUCTF 2021 新生赛]ez_caesar007[SWPUCTF 2021 新生赛]crypto10008[鹤城杯 2021]A_CRYPTO009[SW…...
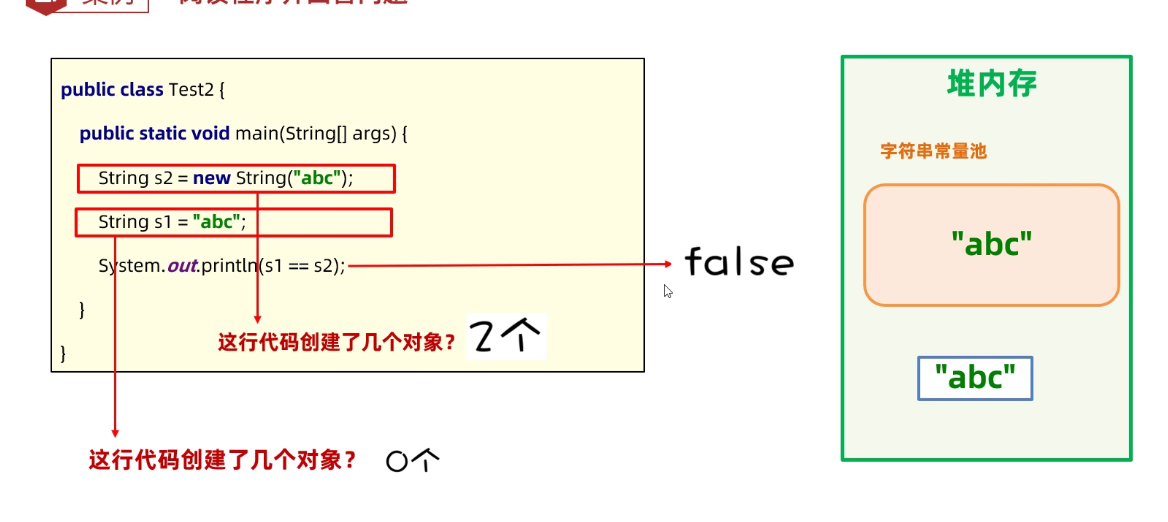
Day03:注意事项、this关键字、构造器、JavaBean、String、ArrayList
OOP的注意事项 类名要跟class文件名一致(一个class可以有多个类,但只有一个public,且与文件名一致),命名介意大驼峰;如果某个对象没有变量指向他,就成垃圾对象了(空指针)…...

【从0到1设计一个网关】性能优化---缓存
文章目录 为什么要用缓存?Caffeine Cache使用Caffeine效果演示为什么要用缓存? 首先先了解一下为什么在网关中我们需要用到缓存。 我们可以从如下几点来入手这个问题: 处理大规模流量: 网关是系统的入口,需要处理大规模的请求流量。高性能的网关能够快速而有效地处理大量…...

Typescript -尚硅谷
基础 1.ts是以js为基础构建的语言,是一个js的超集(对js进行了扩展); 2.ts(type)最主要的功能是在js的基础上引入了类型的概念; Js的类型是只针对于值而言,ts的类型是针对于变量而言 Ts可以被编译成任意版本的js,从而进一步解决了…...
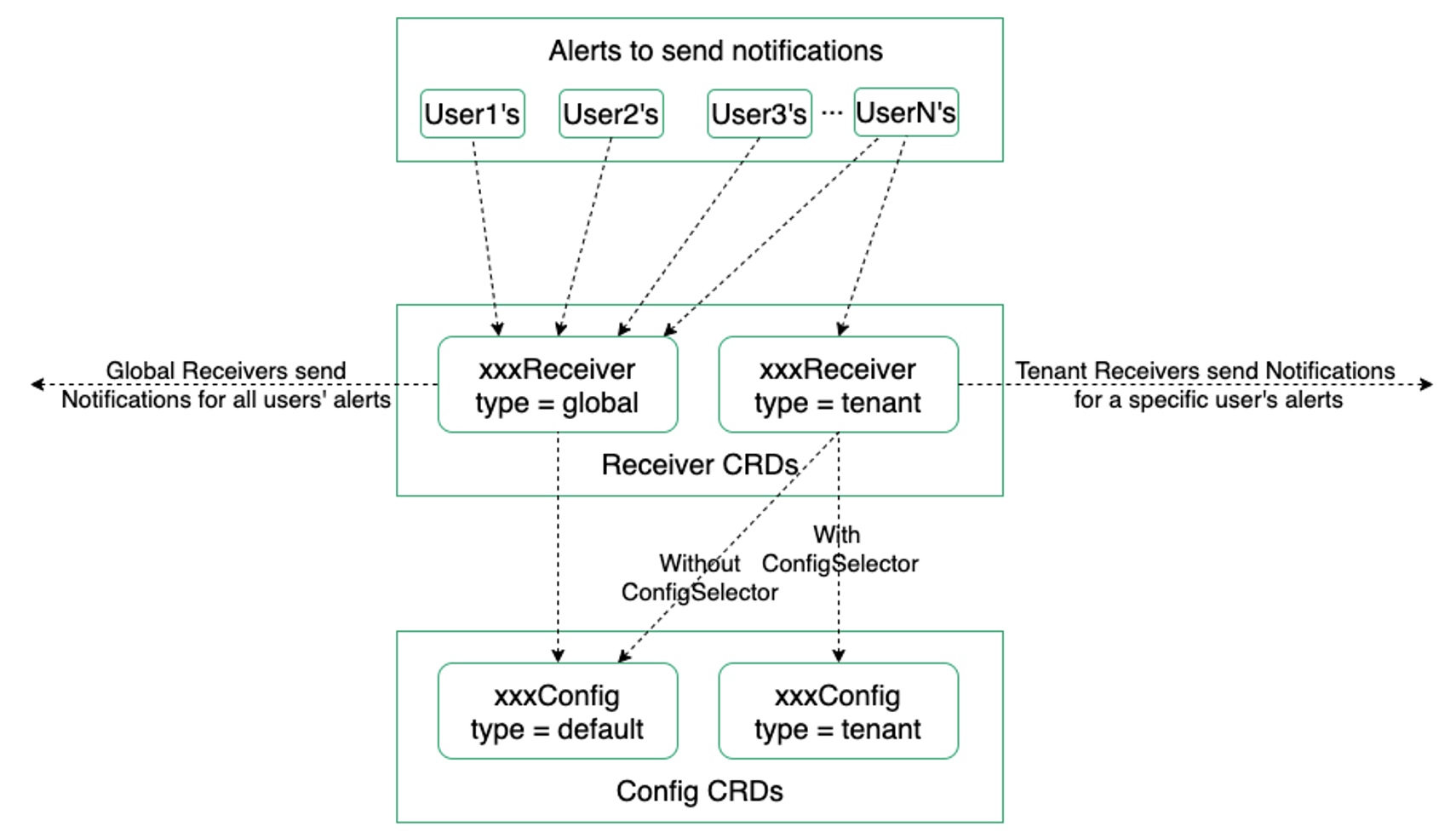
以 Kubernetes 原生方式实现多集群告警
作者:向军涛、雷万钧 来源:2023 上海 KubeCon 分享 可观测性来源 在 Kubernetes 集群上,各个维度的可观测性数据,可以让我们及时了解集群上应用的状态,以及集群本身的状态。 Metrics 指标:监控对象状态的量…...
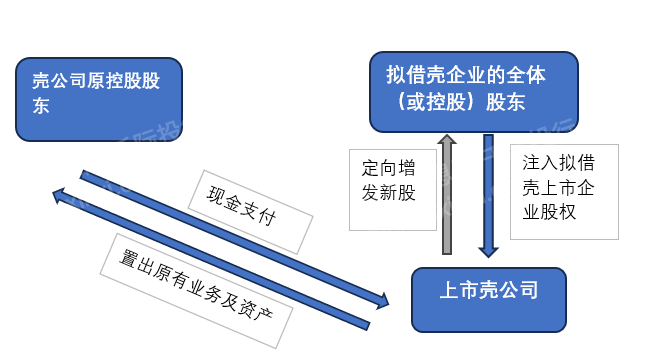
2023年A股借壳上市研究报告
第一章 借壳上市概况 1.1 定义 借壳上市作为一种独特的资本市场操作手法,历来是企业拓展融资渠道和实现市场战略目标的重要途径。具体来说,借壳上市可分为狭义与广义两种模式。在狭义的定义下,借壳上市是指一家已上市的公司的控股母公司&am…...
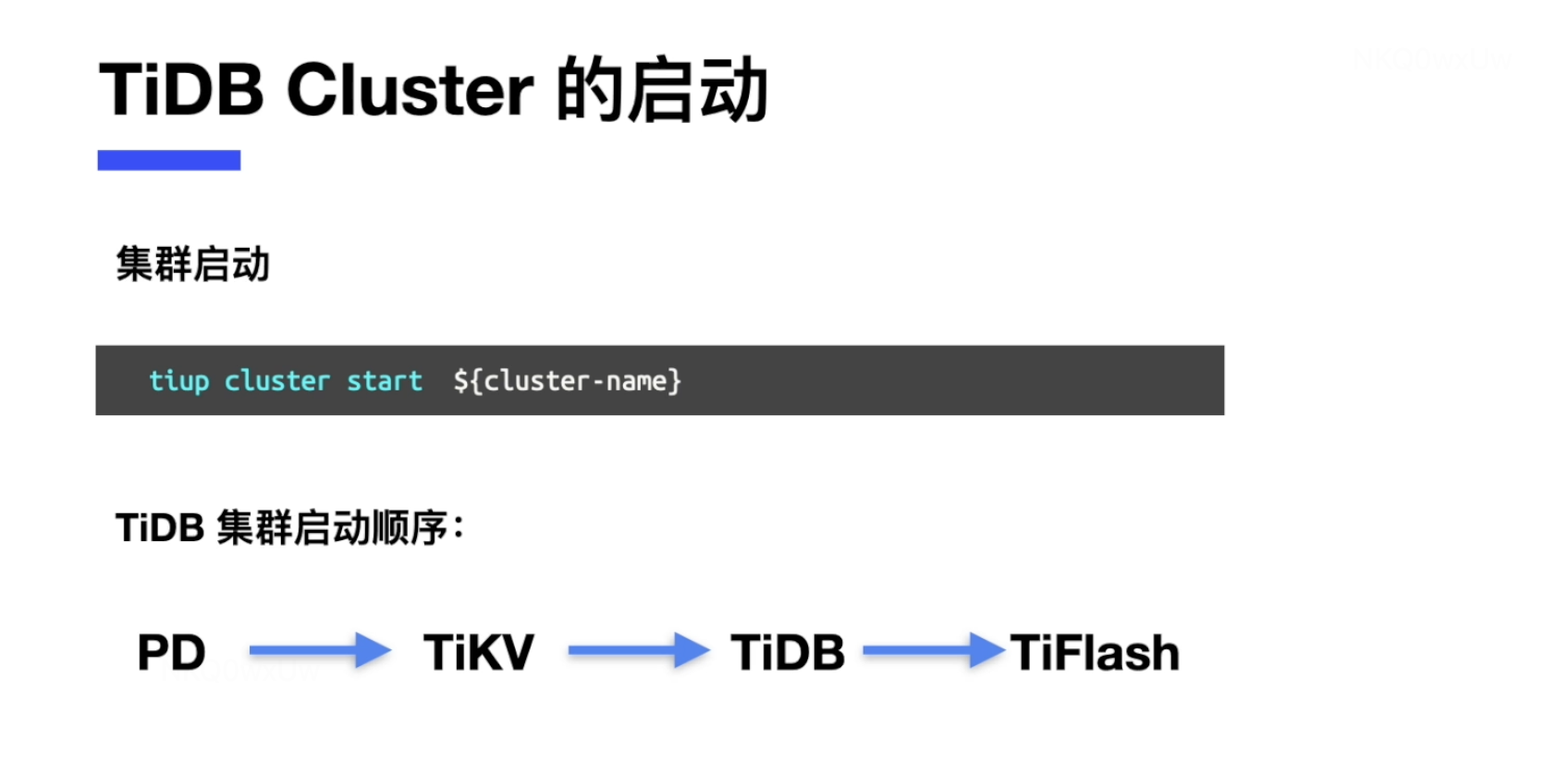
【TiDB】TiDB CLuster部署
目录 0 大纲 一 集群部署工具TiUP简介 1 TiUP 简介 2 TiUP使用 3 TiUP使用举例 二 TiDB Cluster安装配置需求 1 生产环境硬件需求 2 操作系统需求 三 TIDB部署 1 软硬件需求以及前置检查编辑 2 安装TiUP 组件 3 集群拓扑文件 4 执行部署命令 (1&…...

odoo16 库存初始化 excel导入问题
最近在为一家公司实施odoo时,发现库存模块实施过程中按用户实际,产品初始化就是个问题。下面一一记录下 一个新公司,产品都有上百种,甚致几千种,如何把现有产品数据录入系统就是个不小的活。odoo16是有导入导出功能不…...
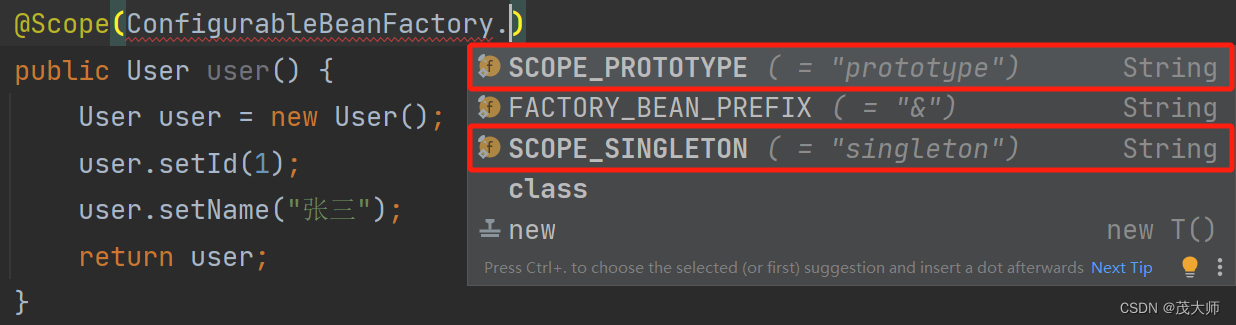
2023.11.11 关于 Spring 中 Bean 的作用域
目录 Bean 的作用域 作用域的定义 Singleton(单例作用域) Prototype(原型作用域) Request(请求作用域) Session(会话请求) Application(全局作用域) …...

5 Paimon数据湖之表数据查询详解
更多Paimon数据湖内容请关注:https://edu.51cto.com/course/35051.html 虽然前面我们已经讲过如何查询Paimon表中的数据了,但是有一些细节的东西还需要详细分析一下。 首先是针对Paimon中系统表的查询,例如snapshots\schemas\options等等这些…...

时间序列预测实战(十二)DLinear模型实现滚动长期预测并可视化预测结果
官方论文地址->官方论文地址 官方代码地址->官方代码地址 个人修改代码->个人修改的代码已经上传CSDN免费下载 一、本文介绍 本文给大家带来是DLinear模型,DLinear是一种用于时间序列预测(TSF)的简单架构,DLinear的核…...
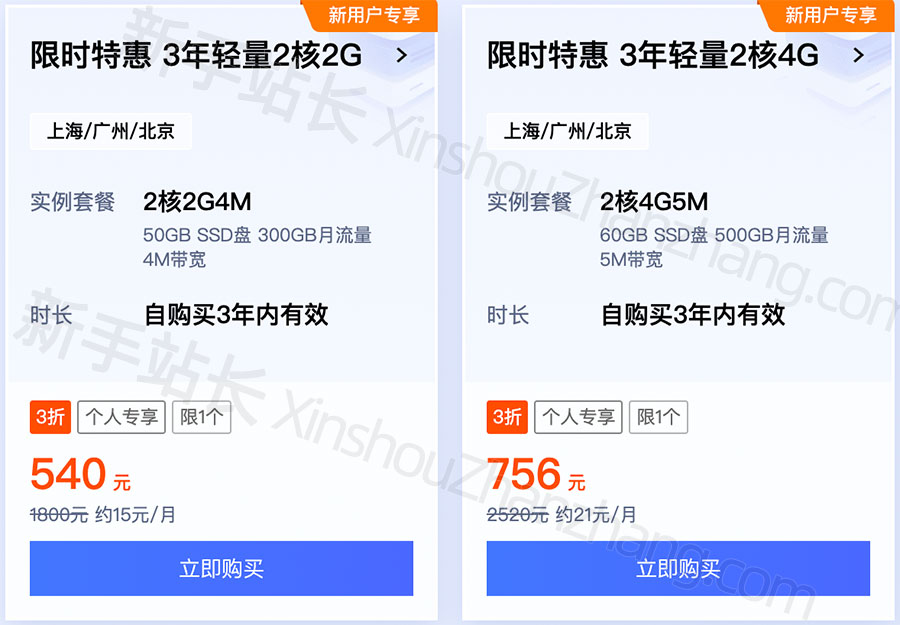
封神教程:腾讯云3年轻量应用服务器老用户购买方法
腾讯云轻量应用服务器特价是有新用户限制的,所以阿腾云建议大家选择3年期轻量应用服务器,一劳永逸,免去续费困扰。腾讯云轻量应用服务器3年优惠可以选择2核2G4M和2核4G5M带宽,3年轻量2核2G4M服务器540元,2核4G5M轻量应…...
 安装最新版的 cmake)
Ubuntu(WSL2) 安装最新版的 cmake
Ubuntu(WSL) 安装最新版的 cmake 具体流程如下: 步骤一:卸载原本的 cmake sudo apt-get remove cmake 步骤二: sudo apt-get update sudo apt-get install apt-transport-https ca-certificates gnupg software-properties-common wget 步…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
