【数据结构】树与二叉树(十一):二叉树的层次遍历(算法LevelOrder)
文章目录
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- 5.2.4 二叉树的遍历
- 1-3 先序、中序、后序遍历递归实现及相关练习
- 4. 中序遍历非递归
- 5. 后序遍历非递归
- 6. 先序遍历非递归
- 7. 层次遍历
- a. 算法LevelOrder
- b. 算法解读
- c. 时间复杂度
- d.代码实现
- levelOrder
- create
- enqueue
- dequeue
- 8. 代码整合
5.2.1 二叉树
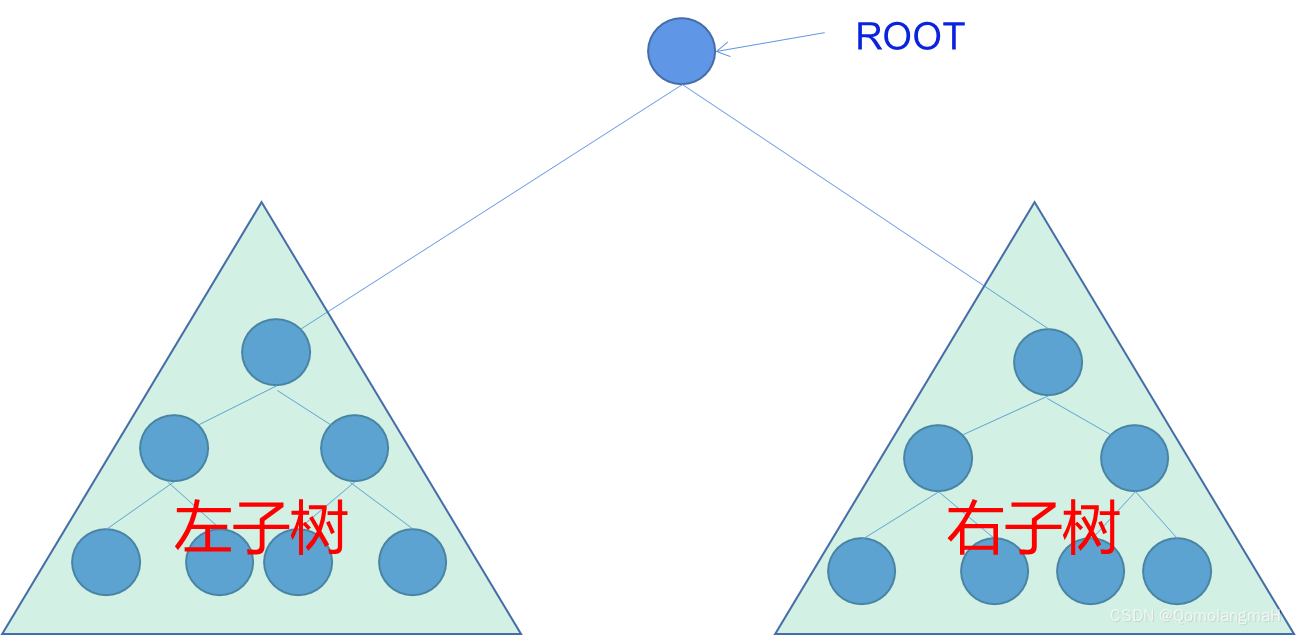
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
二叉树性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
满二叉树、完全二叉树定义、特点及相关证明
- 详细证明过程见前文:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中,详见:
【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
5.2.3 二叉树链接存储
二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中,结点之间的关系用指针说明。在链式存储中,每个二叉树结点都包含三个域:数据域(Data)、左指针域(Left)和右指针域(Right),用于存储结点的信息和指向子结点的指针,详见:
【数据结构】树与二叉树(六):二叉树的链式存储
5.2.4 二叉树的遍历
- 遍历(Traversal)是对二叉树中所有节点按照一定顺序进行访问的过程。
- 通过遍历,可以访问树中的每个节点,并按照特定的顺序对它们进行处理。
- 对二叉树的一次完整遍历,可给出树中结点的一种线性排序。
- 在二叉树中,常用的遍历方式有三种:先序遍历、中序遍历和后序遍历。
- 这三种遍历方式都可以递归地进行,它们的区别在于节点的访问顺序。
- 在实现遍历算法时,需要考虑递归终止条件和递归调用的顺序。
- 还可以使用迭代的方式来实现遍历算法,使用栈或队列等数据结构来辅助实现。
- 遍历是二叉树中基础而重要的操作,它为其他许多操作提供了基础,如搜索、插入、删除等。
1-3 先序、中序、后序遍历递归实现及相关练习
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
4. 中序遍历非递归
【数据结构】树与二叉树(八):二叉树的中序遍历(非递归算法NIO)
5. 后序遍历非递归
【数据结构】树与二叉树(九):二叉树的后序遍历(非递归算法NPO)
6. 先序遍历非递归
【数据结构】树与二叉树(十):二叉树的先序遍历(非递归算法NPO)
7. 层次遍历
层次遍历按层数由小到大,即从第0层开始逐层向下,同层中由左到右的次序访问二叉树的所有结点。
a. 算法LevelOrder

b. 算法解读
- 创建一个队列Q。
- 将指针p指向二叉树T的根节点。
- 如果p不为空,则将p入队列Q。
- 当队列Q非空时,执行以下操作:
- 将队首元素p出队列。
- 打印p的数据。
- 如果p的左子节点不为空,则将左子节点入队列Q。
- 如果p的右子节点不为空,则将右子节点入队列Q。
使用队列来保存待访问的节点,保证按层次遍历的顺序进行访问。首先将根节点入队列,然后通过循环,每次从队列中取出一个节点,访问该节点的数据,并将其左右子节点(如果存在)依次入队列。这样就可以按照层次遍历的顺序逐层访问二叉树的节点。
c. 时间复杂度
这个算法的时间复杂度是O(n),其中n是二叉树中节点的数量。因为每个节点都会入队列一次,出队列一次,所以总的入队和出队操作次数为2n,所以时间复杂度为O(n)。
d.代码实现
levelOrder
void levelOrder(struct Node* root) {if (root == NULL) {return;}struct Queue* front, * rear;create(&front, &rear);enqueue(&front, &rear, root);while (front != NULL) {struct Node* current = front->node;printf("%c ", current->data);if (current->left != NULL) {enqueue(&front, &rear, current->left);}if (current->right != NULL) {enqueue(&front, &rear, current->right);}dequeue(&front);}
}其中,队列操作详解:【数据结构】线性表(九)队列:链式队列及其基本操作(初始化、判空、入队、出队、存取队首元素)
create
// 初始化队列
void create(struct Queue** front, struct Queue** rear) {*front = *rear = NULL;
}
enqueue
// 入队列
void enqueue(struct Queue** front, struct Queue** rear, struct Node* node) {struct Queue* temp = (struct Queue*)malloc(sizeof(struct Queue));if (temp == NULL) {printf("Memory allocation failed!\n");exit(1);}temp->node = node;temp->next = NULL;if (*rear == NULL) {*front = *rear = temp;return;}(*rear)->next = temp;*rear = temp;
}
dequeue
// 出队列
void dequeue(struct Queue** front) {if (*front == NULL) {return;}struct Queue* temp = *front;*front = (*front)->next;free(temp);
}8. 代码整合
#include <stdio.h>
#include <stdlib.h>// 二叉树结点的定义
struct Node {char data;struct Node* left;struct Node* right;
};// 创建新结点
struct Node* createNode(char data) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));if (newNode == NULL) {printf("Memory allocation failed!\n");exit(1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 创建队列
struct Queue {struct Node* node;struct Queue* next;
};// 初始化队列
void create(struct Queue** front, struct Queue** rear) {*front = *rear = NULL;
}// 入队列
void enqueue(struct Queue** front, struct Queue** rear, struct Node* node) {struct Queue* temp = (struct Queue*)malloc(sizeof(struct Queue));if (temp == NULL) {printf("Memory allocation failed!\n");exit(1);}temp->node = node;temp->next = NULL;if (*rear == NULL) {*front = *rear = temp;return;}(*rear)->next = temp;*rear = temp;
}// 出队列
void dequeue(struct Queue** front) {if (*front == NULL) {return;}struct Queue* temp = *front;*front = (*front)->next;free(temp);
}// 层次遍历二叉树
void levelOrder(struct Node* root) {if (root == NULL) {return;}struct Queue* front, * rear;create(&front, &rear);enqueue(&front, &rear, root);while (front != NULL) {struct Node* current = front->node;printf("%c ", current->data);if (current->left != NULL) {enqueue(&front, &rear, current->left);}if (current->right != NULL) {enqueue(&front, &rear, current->right);}dequeue(&front);}
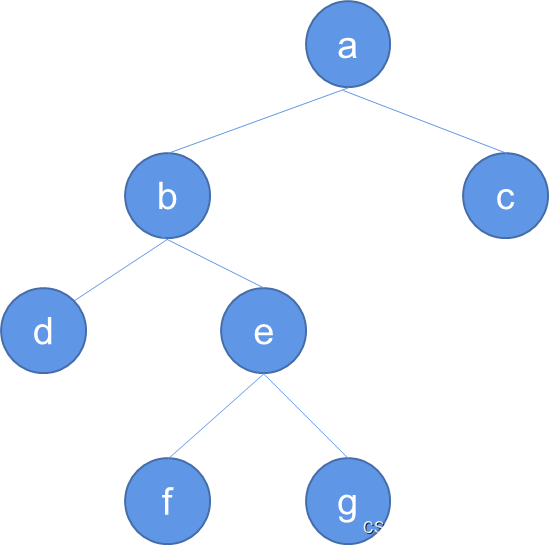
}int main() {// 创建一棵二叉树struct Node* root = createNode('a');root->left = createNode('b');root->right = createNode('c');root->left->left = createNode('d');root->left->right = createNode('e');root->left->right->left = createNode('f');root->left->right->right = createNode('g');// 层次遍历二叉树printf("层次遍历二叉树: \n");levelOrder(root);printf("\n");return 0;
}
相关文章:

【数据结构】树与二叉树(十一):二叉树的层次遍历(算法LevelOrder)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...
【PyQt】(自制类)处理鼠标点击逻辑
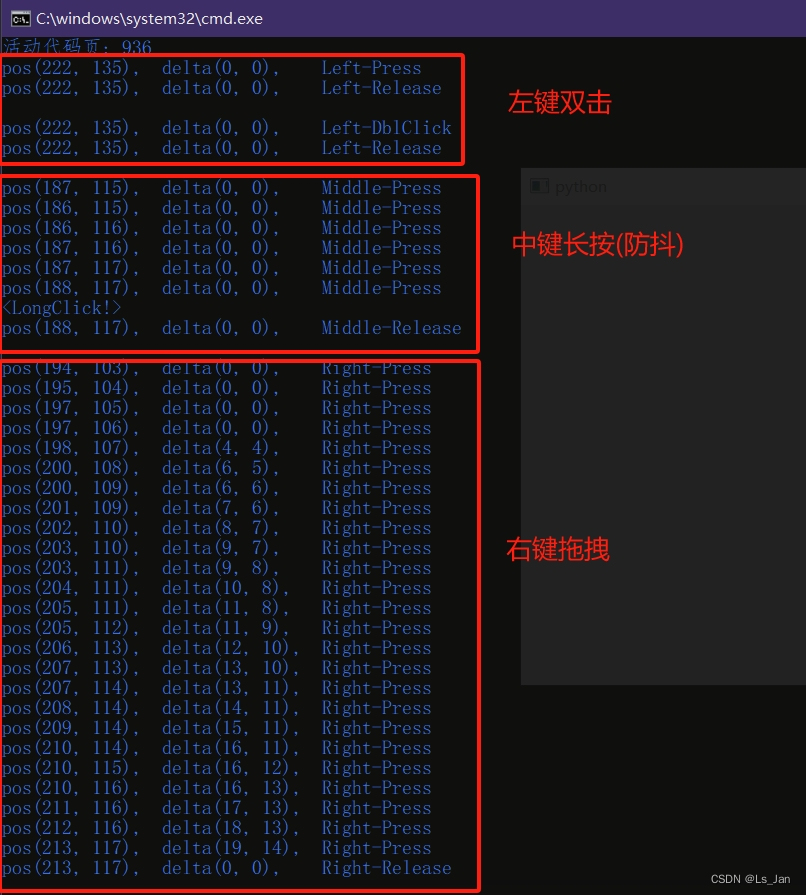
写了个自认为还算不错的类,用于简化mousePressEvent、mouseMoveEvent和mouseReleaseEvent中的鼠标信息。 功能有以下几点: 鼠标当前状态,包括鼠标左/中/右键和单击/双击/抬起鼠标防抖(仅超出一定程度时才判断鼠标发生了移动),灵…...
JAVA IDEA 下载
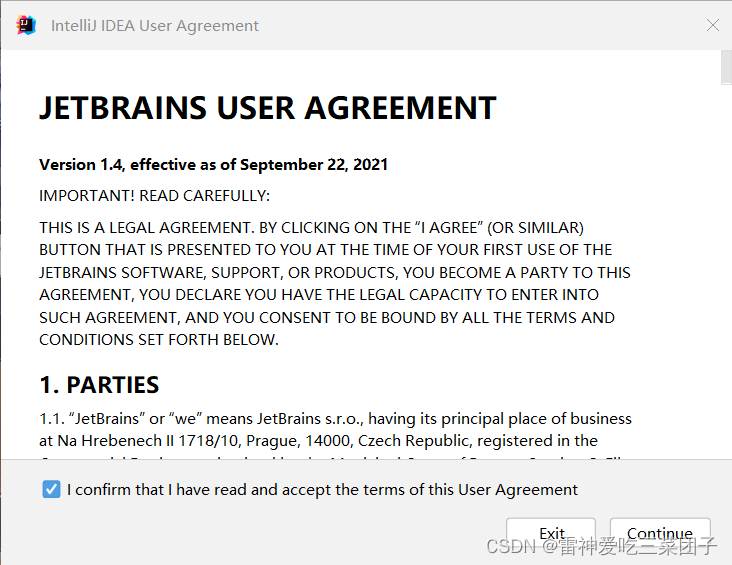
超简单步骤一: IntelliJ IDEA 官方下载链接 点击以上链接进入下图,点击下载 继续点下载,然后等待下载完后打开安装包即可 步骤二: 打开下好的安装包,点击Browse...我们把它下载到自己喜欢的地方(主要是别占…...

DevOps简介
DevOps简介 1、DevOps的起源2、什么是DevOps3、DevOps的发展现状4、DevOps与虚拟化、容器 1、DevOps的起源 上个世纪40年代,世界上第一台计算机诞生。计算机离不开程序(Program)驱动,而负责编写程序的人,被称为程序员&…...

体验前所未有的显示器管理体验:BetterDisplay Pro Mac
在现代的数字化时代,显示器是我们日常生活和工作中不可或缺的一部分。从笔记本电脑到台式机,从平板电脑到手机,几乎所有的电子设备都配备了显示器。然而,对于专业人士和从事设计行业的人来说,仅仅依靠系统自带的显示器…...

python用pyinstaller打包exe,去掉黑窗口
使用Python编写程序将Python脚本打包成可执行文件(EXE),但是会有一个命令框产生,很烦,所以,去掉这个框 1,安装pyinstaller pip install pyinstaller2,打包产生cmd命令框 pyinstaller --onefi…...
如何关闭Windows Defender(亲测可行!!非常简单)
一、背景 Windows Defender(简称WD)真的太讨厌了,经常给你报你下载的文件是病毒,且不说真的是不是病毒,它都不询问直接删。 另外聚资料显示WD还会不合时宜地执行扫描导致系统变慢(不会在合适的、空闲的时…...

【objectarx.net】创建多重引线
创建多重引线...

【objectarx.net】创建组,列出所有组,查找实体所在的组
创建组,列出所有组...

Llama2通过llama.cpp模型量化 WindowsLinux本地部署
Llama2通过llama.cpp模型量化 Windows&Linux本地部署 什么是LLaMA 1 and 2 LLaMA,它是一组基础语言模型,参数范围从7B到65B。在数万亿的tokens上训练的模型,并表明可以专门使用公开可用的数据集来训练最先进的模型,而无需求…...
Coding面试题之手写线程池
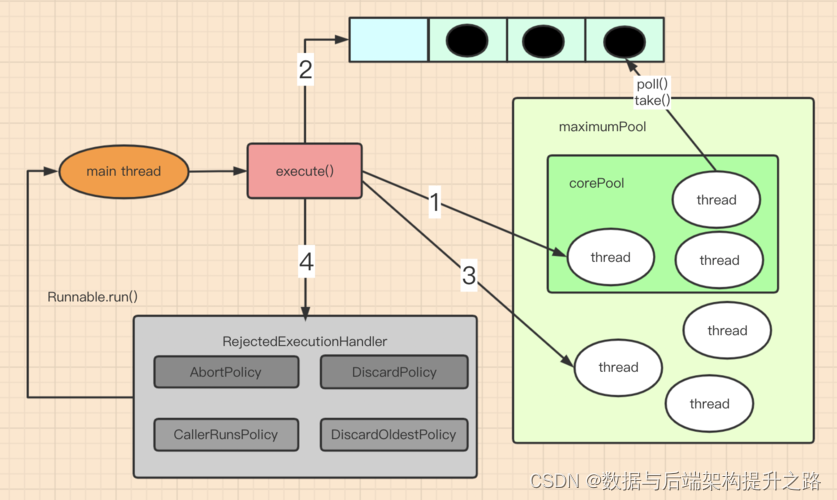
原理图 JDK线程池原理 实现代码 1.线程类(PoolThread) 这个类用于执行任务队列中的任务。 public class PoolThread extends Thread {private final Queue<Runnable> taskQueue;private boolean isStopped false;private long lastTaskTime …...

【objectarx.net】删除零长度曲线和获取零长度曲线的数量
删除零长度曲线和获取零长度曲线的数量...
Win11专业版安装Docker Desktop,并支持映射主机的gpu
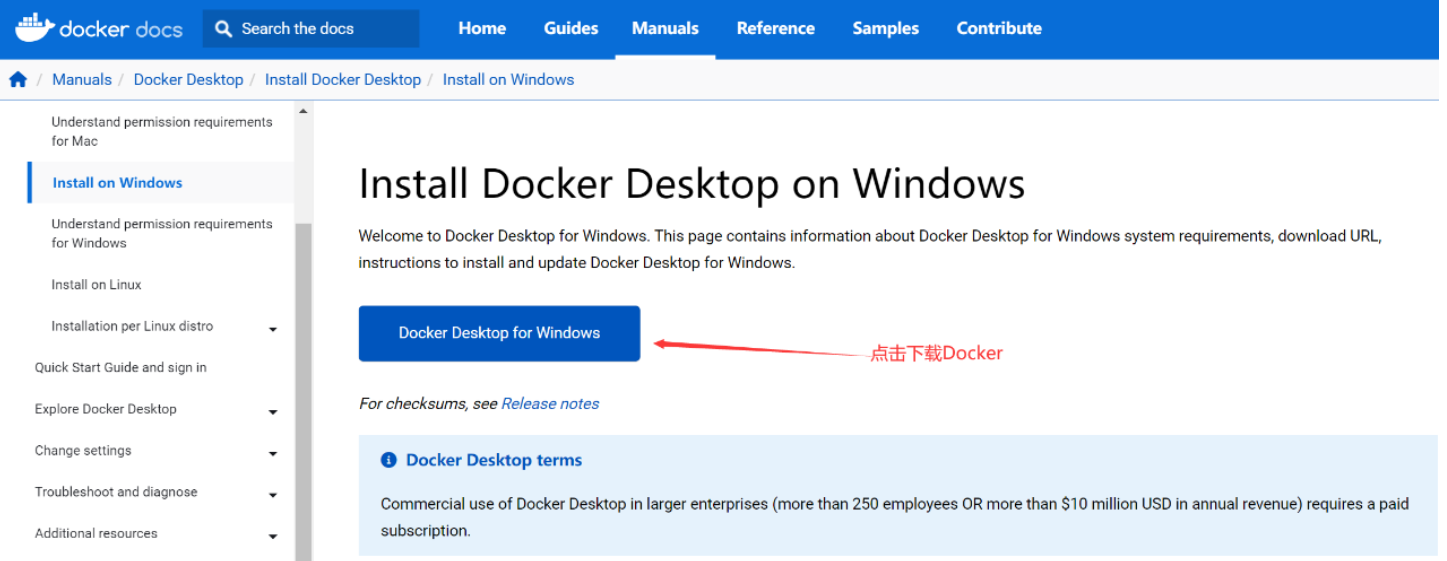
一、Windows环境下安装 Docker 必须满足: 1. 64位Windows 11 Pro(专业版和企业版都可以) 2. Microsoft Hyper-V,Hyper-V是微软的虚拟机,在win11上是自带的,我们只需要启动就可以了 二、下载Docker Desktop安装包 方式一:进入官网下载 https://docs.docker.com/desktop…...

Mac代码文本编辑器Sublime Text 4
Sublime Text 4 for Mac拥有快速响应的功能,可以快速加载文件和执行命令,并提供多种语言支持,包括C 、Java、Python、HTML、CSS等。此外,该编辑器还支持LaTeX、Markdown、JSON、XML等技术领域。 Sublime Text 4 for Mac的插件丰富…...

MATLAB中plot函数用法
目录 语法 说明 向量和矩阵数据 表数据 其他选项 示例 创建线图 绘制多个线条 根据矩阵创建线图 指定线型 指定线型、颜色和标记 在特定的数据点显示标记 指定线宽、标记大小和标记颜色 添加标题和轴标签 绘制持续时间并指定刻度格式 基于表绘制坐标 在一个轴…...

win10 安装vscode
1 Download Visual Studio Code - Mac, Linux, Windows 2 this user installer is not meant to be run as an administrator . if ou would like to install vs code for all users i this sys download the system installer instead form are u want to con 提示的意思是&a…...
MATLAB中Arrow 属性说明
目录 颜色和样式 位置 Arrow 属性是箭头的外观和行为。 Arrow 属性控制 Arrow 对象的外观和行为。通过更改属性值,可以修改箭头的特定方面。使用圆点表示法查询和设置属性。 ar annotation("arrow"); c ar.Color; ar.Color "red"; 颜色和…...

MYSQL 慢查询和慢查询日志
在数据库管理中,慢查询是指执行时间较长的 SQL 查询语句。这类查询可能导致系统性能下降,影响用户体验。为了帮助识别和解决这些性能问题,数据库管理系统通常提供了慢查询日志,用于记录执行时间超过一定阈值的查询。本文将深入探讨…...
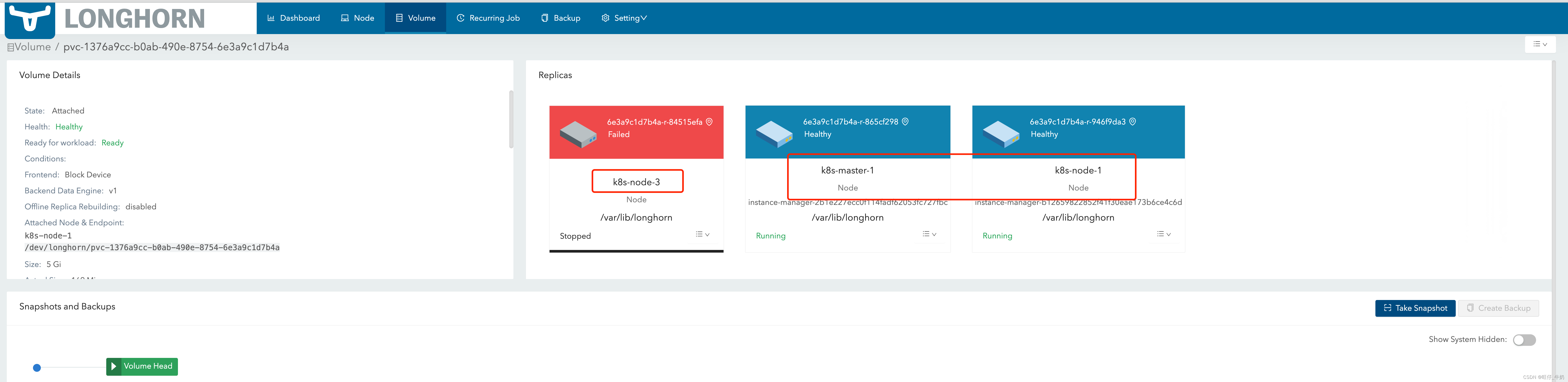
Longhorn跨AZ实现存储高可用
Longhorn跨AZ实现存储高可用 longhorn基础组件功能及其作用这里就不做介绍了 方案一 Longhorn跨AZ的高可用的就是一个PVC的replicas 均匀打散的不同的AZ区域之间,这样当某个AZ挂掉后,engine会立即使用另外一个数据副本,并重建这个副本&…...
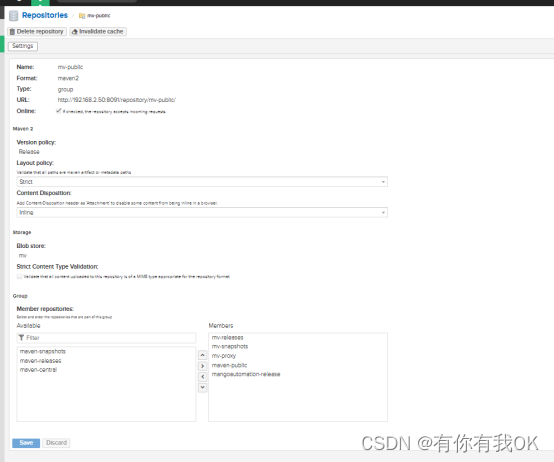
maven 私有仓库配置
1.整体库信息 2.配置阿里云库 (可以配置多个库,再引用代理库) 3.建立自己的 发布,快照库 4.建立自由的公共库- 引用所有需要的库 5.maven setting 中配置 用户名密码 <server><id>mv-releases</id><usernam…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
