Java必刷入门递归题×5(内附详细递归解析图)

目录
1.求N的阶乘
2.求1+2+...+N的和
3.顺序打印数字的每一位
4.求数字的每一位之和
5.求斐波拉契数列
1.求N的阶乘
(1)解析题目意思
- 比如求5的阶乘,符号表示就是5!;所以5!=5*4*3*2*1
- 我们下面使用简单的递归完成本题,看递归代码
public static int sub(int n) {if(n==1) {return 1;}return n * sub(n-1);}- 下面解析该代码的意思
(2)递归思路
- 拆解算法:6!=6*5!;5!=5*4!;4!=4*3!;3!=3*2!;2!=2*1!;其实也就是6!=6*5*4*3*2*1。
- 用代码表示:整体可能有点乱,需要读者静下心来理解
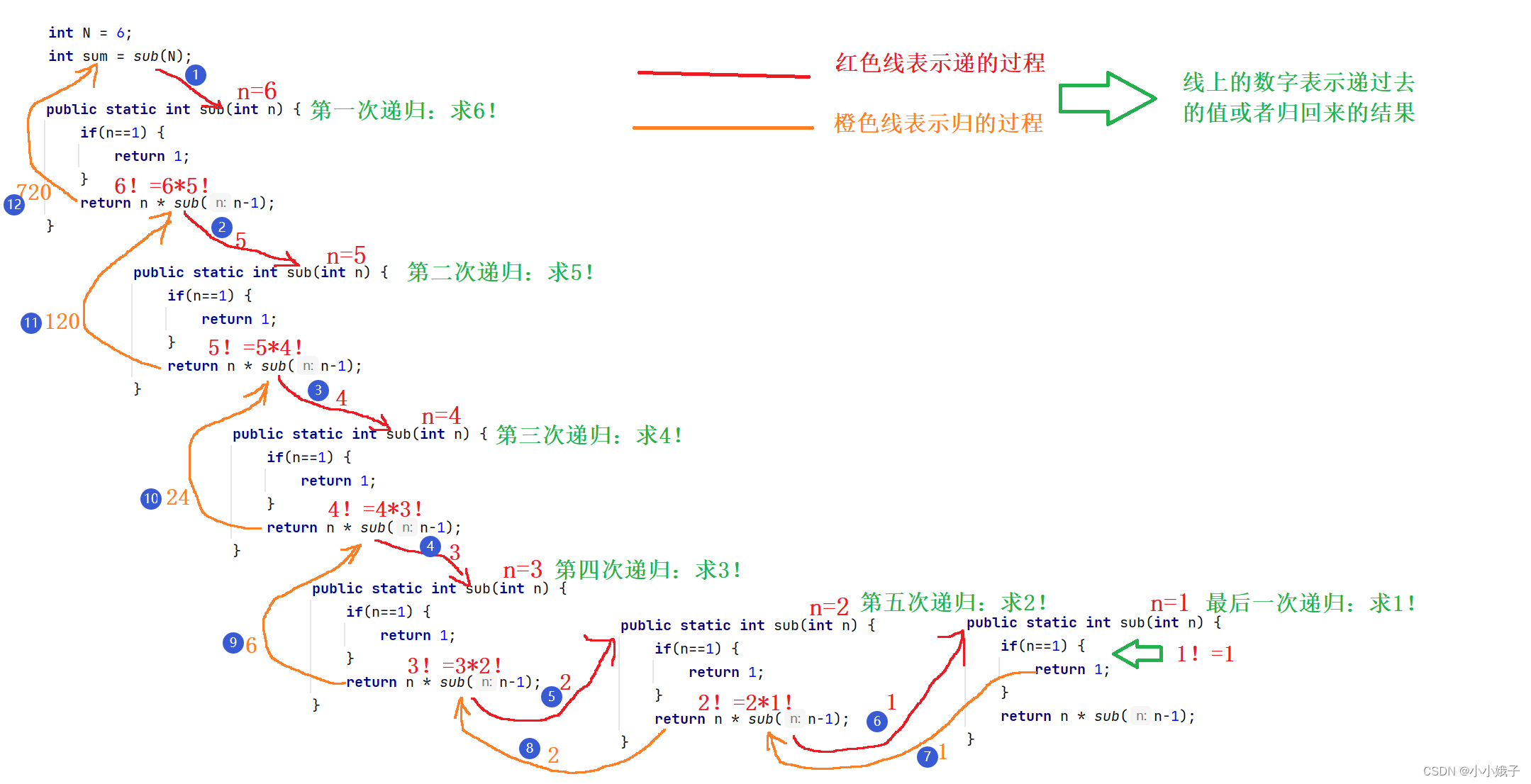
(3)完整代码
public static void main3(String[] args) {//递归求N的阶乘 int N = 6;int sum = sub(N);System.out.println(sum);}public static int sub(int n) {if(n==1) {return 1;}return n * sub(n-1);}2.求1+2+...+N的和
(1)解析题目意思
- 假设N=3,意思是求从1加到N的和(1+2+3)
- 假设N=4,则需要求(1+2+3+4)的和
(2)递归思路
- 我们这里以N=3举例
- 思路:求(1+2+3)可以拆解成:3+(求N=2的和),求N=2的和可以拆解成:2+(求N=1的和)
- 得出递归代码
public static int sum(int n) {if(n==1) {return 1;}return n+sum(n-1);}- 下面剖解递归思路:
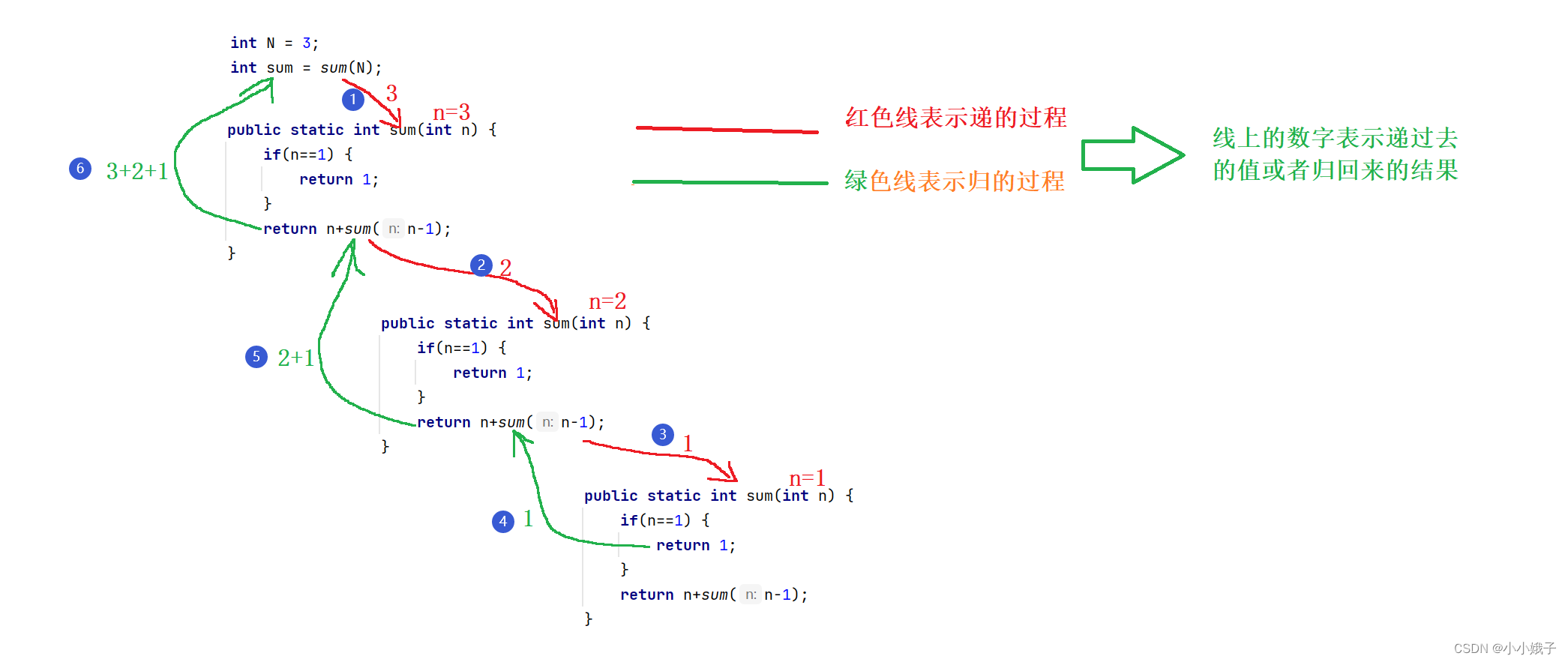
(3)完整代码
public static void main(String[] args) {//递归求和int N = 3;int sum = sum(N);System.out.println(sum);}public static int sum(int n) {if(n==1) {return 1;}return n+sum(n-1);}3.顺序打印数字的每一位
(1)解析题目意思
- 比如打印1234,要题目意思打印的结果就是1 2 3 4(中间隔开)
(2)解析递归思路
- 假设输入的数据是1234,打印出1 2 3 4
- 思路:要打印1 2 3 4,就要先打印1 ,再打印2 3 4 ;打印2 3 4 ,就要先打印2 ,再打印3 4 ;打印3 4,就要先打印3 ,再打印4
- 利用/10去掉最低位,%10得到最低位的思路进行
- 得出递归代码
public static void print(int n) {if(n<10) {System.out.print(n+" ");return;}print(n/10);System.out.print(n%10+" ");}- 解析递归思路
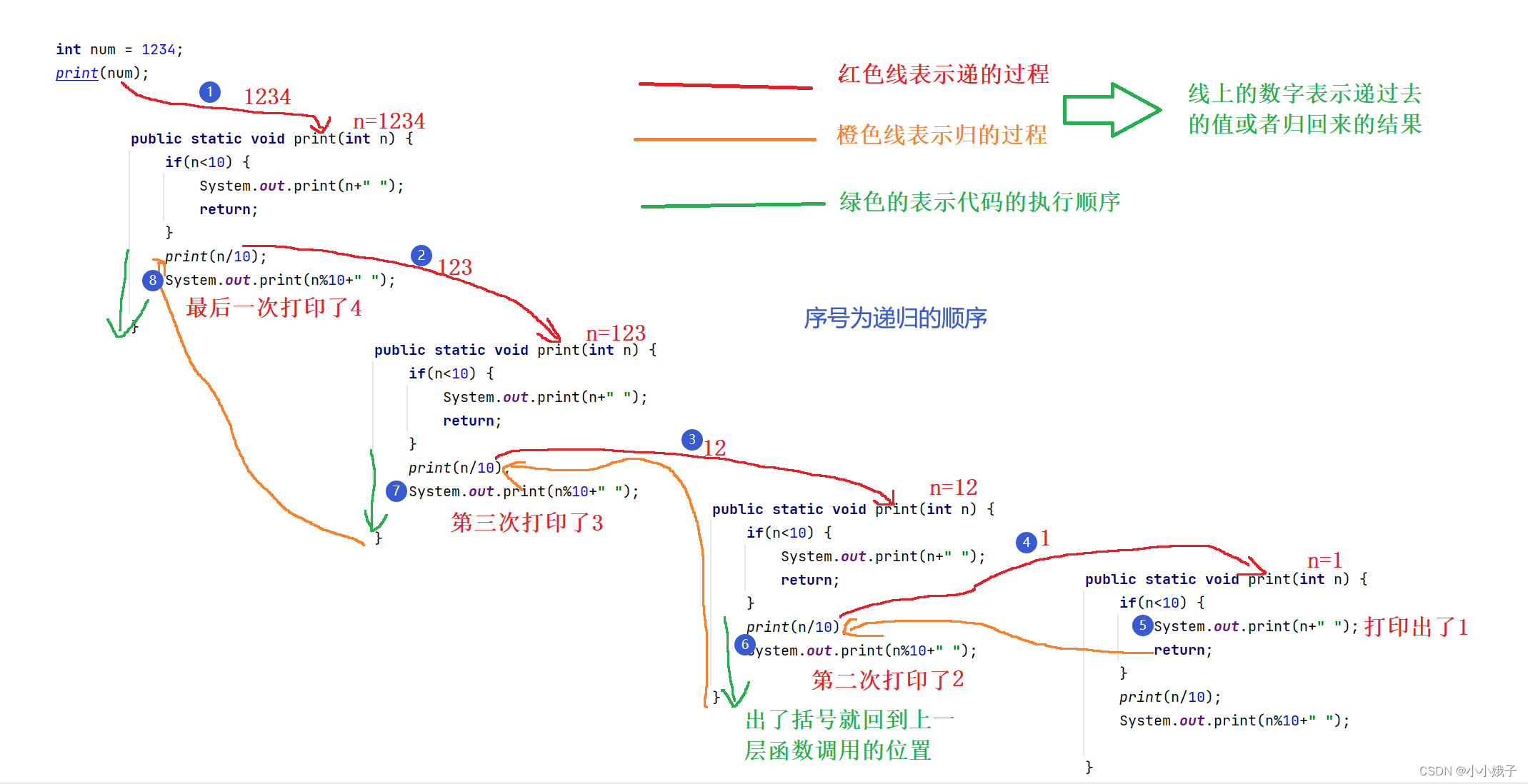
(3)完整代码
public static void main(String[] args) {//顺序打印数组的每一位int num = 1234;print(num);}public static void print(int n) {if(n<10) {System.out.print(n+" ");return;}print(n/10);System.out.print(n%10+" ");}4.求数字的每一位之和
(1)解析题目
- 比如给出数字:1345,就需要求1+3+4+5的和
(2)解析递归思路
- 我们这里以求1234的每一位之和
- 同样利用/10去掉最低位,%10得到最低位的思路
- 思路:求1234的每一位之和,可以求4+123的每一位之和;求123的每一位之和,可以求3+12的每一位之和;求12的每一位之和,可以求1+2的每一位之和
- 递归代码
public static int sumEvery(int n) {if(n==1) {return n;}return n%10+sumEvery(n/10);}- 递归过程解析
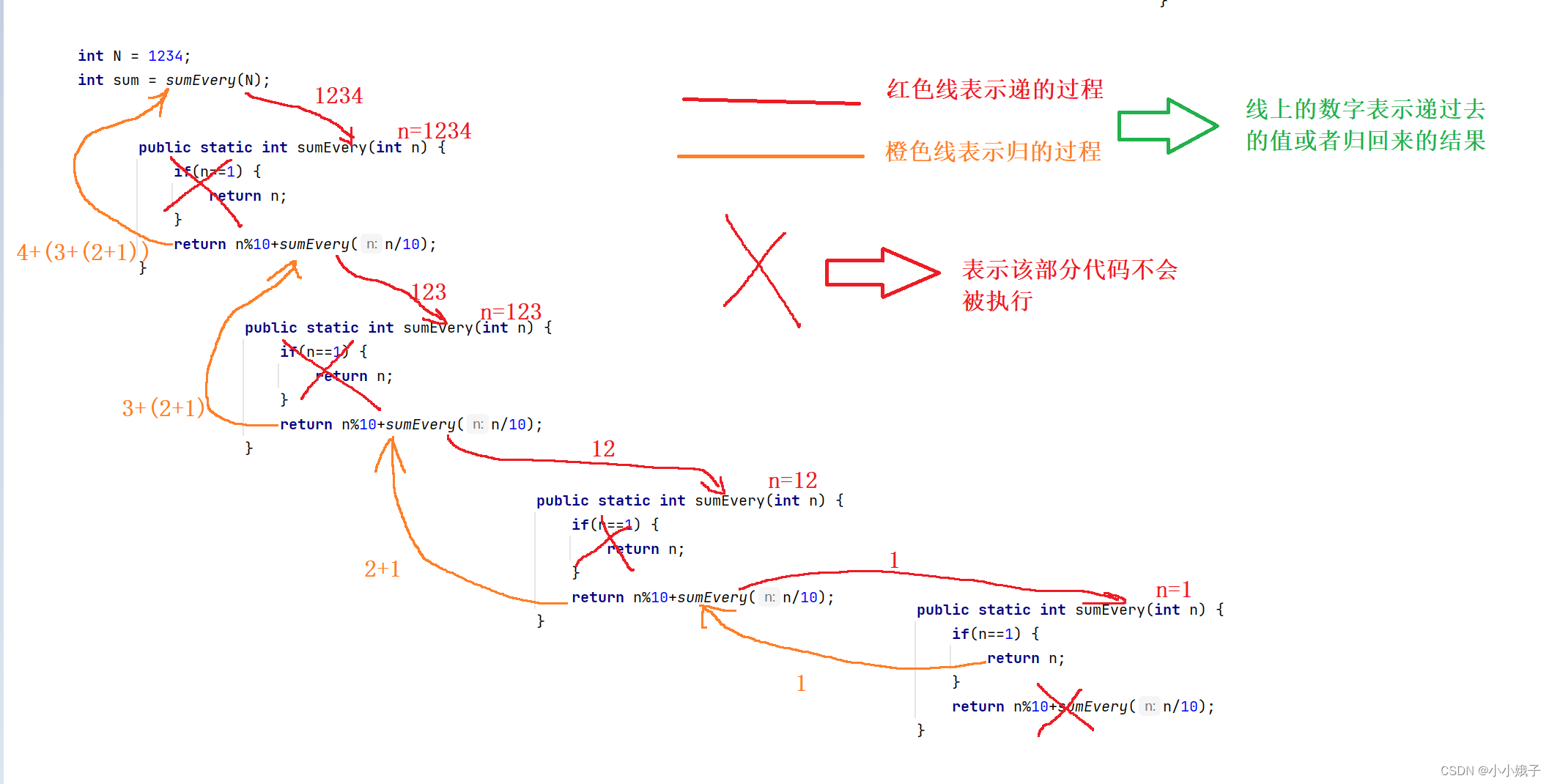
(3)完整代码
public static void main(String[] args) {//求数字的每一位之和int N = 1234;int sum = sumEvery(N);System.out.println(sum);}public static int sumEvery(int n) {if(n==1) {return n;}return n%10+sumEvery(n/10);}5.求斐波拉契数列
(1)了解斐波拉契数列
- 斐波那契数列,其数值为:1、1、2、3、5、8、13、21、34……这个数列从第3项开始,每一项都等于前两项之和。
(2)递归思路求解
- 比如求第五个斐波那契数(5):5=3(第四个数)+2(第三个数);3=2(第三个数)+1(第二个数);以此类推,直到n<=2。
- 递归部分代码
public static int fib(int n) {if(n<=2) {return 1;}return fib(n-2)+fib(n-1);}- 递归思路解析

- 递归完整代码
public static void main(String[] args) {//斐波拉契int N = 8;int sum = fib(N);System.out.println(sum);}public static int fib(int n) {if(n<=2) {return 1;}return fib(n-2)+fib(n-1);}(3)迭代思路
- 该思路也就是利用循环去做,可以计算更大的斐波那契数
- 利用:某个数=前面两个数相加,从前面开始往后计算,不断循环即可
- 代码展示:
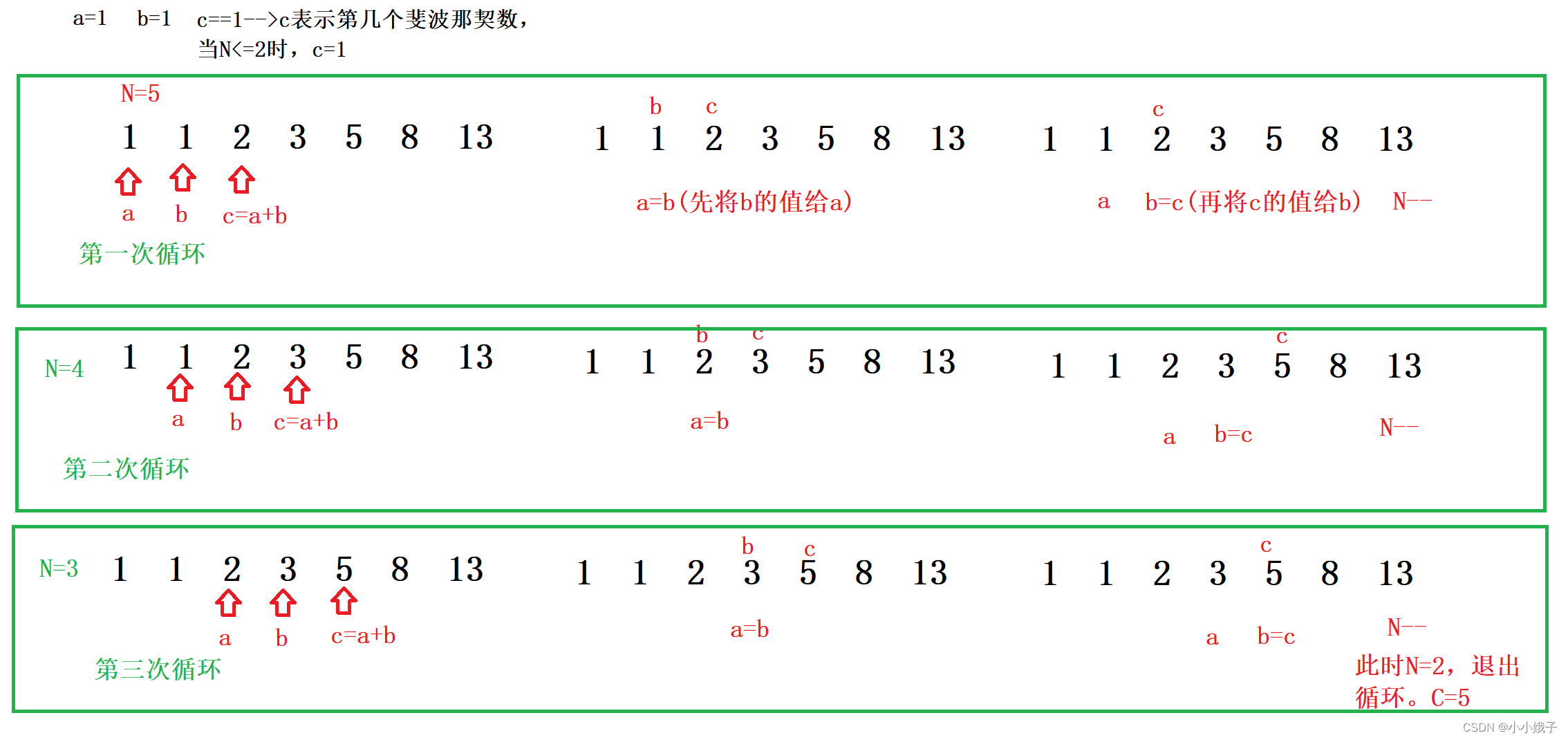
public static void main(String[] args) {//迭代思路int N = 5;int a = 1;int b = 1;int c = 1;while(N>2) {c = a+b;a = b;b = c;N--;}System.out.println(c);}- 迭代思路解析:
本次的五道递归题就结束了
相关文章:

Java必刷入门递归题×5(内附详细递归解析图)
目录 1.求N的阶乘 2.求12...N的和 3.顺序打印数字的每一位 4.求数字的每一位之和 5.求斐波拉契数列 1.求N的阶乘 (1)解析题目意思 比如求5的阶乘,符号表示就是5!;所以5!5*4*3*2*1我们下面使用简单的…...

android 闪屏图适配尺寸
不同的 Android 设备可能具有不同的屏幕尺寸和分辨率,因此最好提供不同尺寸的启动画面图像,以确保与各种设备的兼容性。 以下是 Android 启动画面图像的一些最常见尺寸: 320 x 480像素(肖像) 480 x 320像素࿰…...
与(?m)的区别)
正则表达式中(?s)与(?m)的区别
理论: (?m) 和 (?s) 是正则表达式中的两个模式标志,它们具有不同的作用: (?m) 多行模式标志(也称为 “multiline” 模式): 默认情况下,正则表达式将整个输入字符串视为单行多行文本中使用…...

Clickhouse学习笔记(11)—— 数据一致性
使用合并树引擎时,无论是ReplacingMergeTree还是SummingMergeTree,都只能保证数据的最终一致性,因为数据的去重、聚合等操作会在数据合并的期间进行,而合并会在后台以一个不确定的时间进行,因此无法预先计划࿱…...

【uniapp】六格验证码输入框实现
效果图 代码实现 <view><view class"tips">已发送验证码至<text class"tips-phone">{{ phoneNumber }}</text></view><view class"code-input-wrap"><input class"code-input" v-model"…...

【react hook】在react hook组件中,使用Antd Table组件,columns数据异步获取,list数据更新但没有rerender解决办法
情景描述 我们有一个react组件,显示了一个Antd Table组件,设置了一个columns变量并复制给Table的columns属性,由于我们请求的datasource来源是异步的,示例伪代码如下: const [columns, setColumns] useState([]); /…...
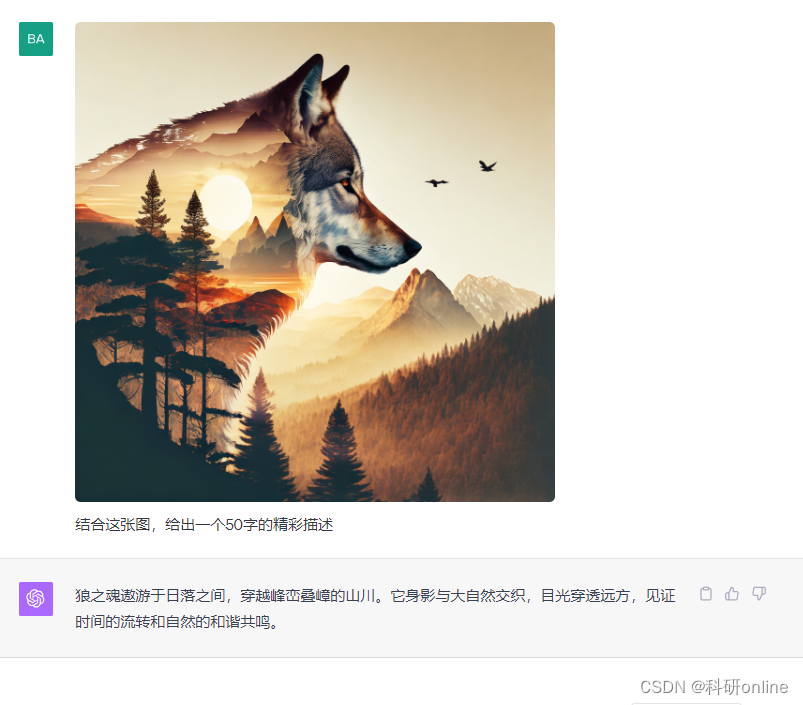
ChatGPT的图识别来了
前几天ChatGPT推出了Dall-E 3功能,可以根据文字和描述一段话来生成一个或者一组图。 这次又来重磅了,图识别又来了!换句话说,也即是文生图,图生文都可以实现了,一起来试试 1、解释图中的意思 ࿰…...

java Stream编程笔记
文章目录 Stream介绍什么是 Stream? Stream中间操作过滤操作(filter)映射操作(map)排序操作(sorted)截断操作(limit 和 skip) Stream 的终止操作forEach 和 peek聚合操作…...

顶顶通语音识别使用说明
介绍 顶顶通语音识别软件(asrproxy)是一个对接了多种语音识别接口的语音识别系统。可私有化部署(支持中文英文和方言等,支持一句话识别、实时流识别、多声道录音文件识别。 原理 asrproxy内嵌了阿里达摩院的开源语音识别工具包FunASR,后续我们也会使用自有的预料…...
重磅发布 OpenAI 推出用户自定义版 ChatGPT
文章目录 重磅发布 OpenAI 推出用户自定义版 ChatGPT个人简介 重磅发布 OpenAI 推出用户自定义版 ChatGPT OpenAI 首届开发者大会 (OpenAI DevDay) 于北京时间 11 月 7 日凌晨 02:00 开始,大会上宣布了一系列平台更新。其中一个重要更新是用户可以创建他们自己的自定…...
读取 json 文件)
Java 幼儿园(20231111)读取 json 文件
1、功能场景 (1)多人合作开发一个功能模块时,需要调用外部接口 (2)对方接口的开发工作还没有完成,只能提供一个返回值的示例文件 json 文件。 (3)返回的 json 数据多达几百个字段。 …...
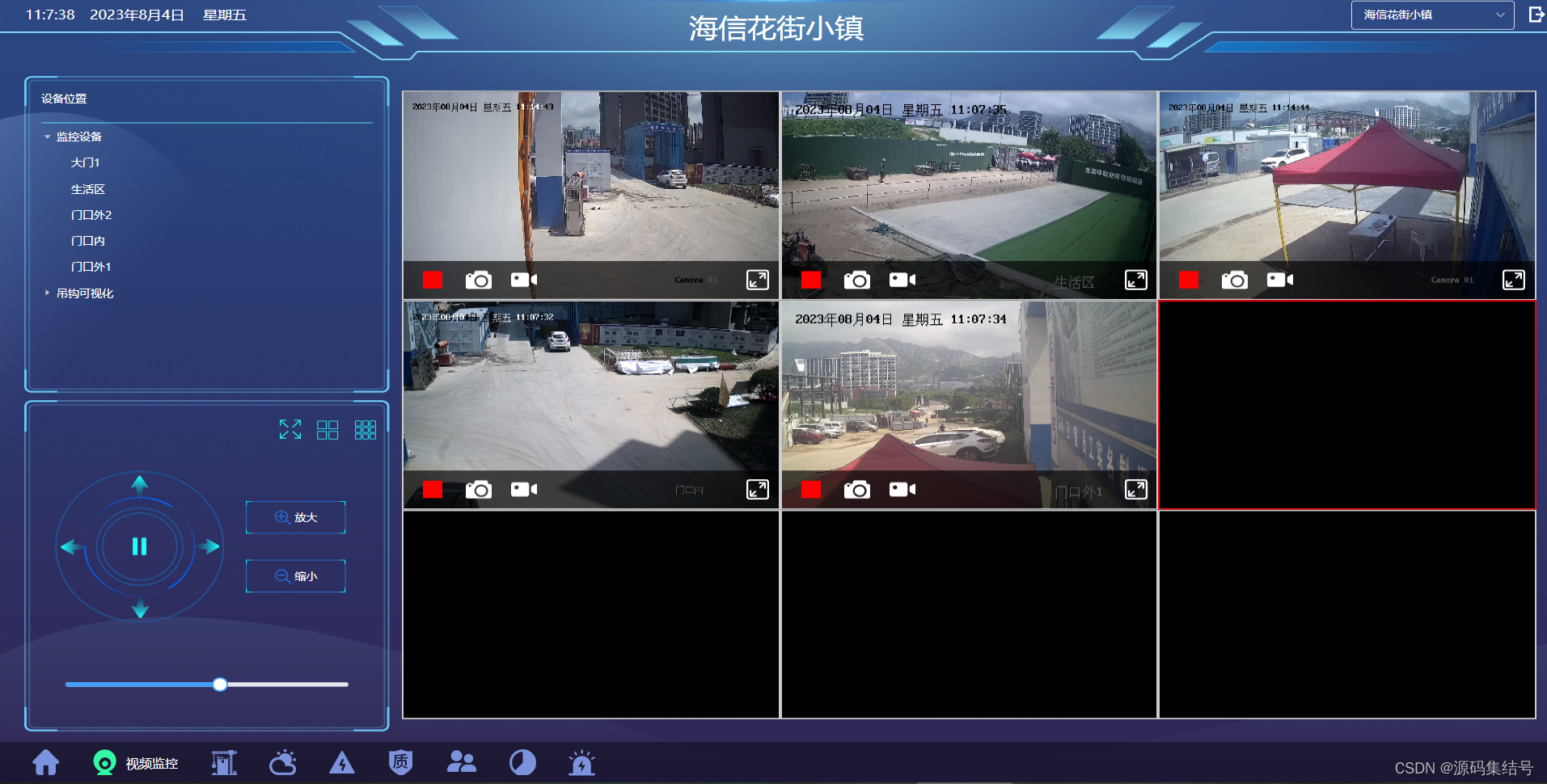
云计算、大数据技术的智慧工地,实现对建筑工地实时监测、管理和控制的一种新型建筑管理方式
智慧工地是利用物联网、云计算、大数据等技术,实现对建筑工地实时监测、管理和控制的一种新型建筑管理方式。 智慧工地架构: 1、终端层: 充分利用物联网技术、移动应用、智能硬件设备提高现场管控能力。通过RFID、传感器、摄像头、手机等终…...

功能案例 -- 通过开关,改变白天和黑夜
效果展示 代码展示 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><style>:root {--default-bac-color: #f…...

Linux编写一个极简版本的Shell
Linux编写一个极简版本的Shell 📟作者主页:慢热的陕西人 🌴专栏链接:Linux 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 本博客主要内容在Linux环境下ÿ…...

亚马逊云AI应用科技创新下的Amazon SageMaker使用教程
目录 Amazon SageMaker简介 Amazon SageMaker在控制台的使用 模型的各项参数 pytorch训练绘图部分代码 Amazon SageMaker简介 亚马逊SageMaker是一种完全托管的机器学习服务。借助 SageMaker,数据科学家和开发人员可以快速、轻松地构建和训练机器学习模型&#…...
转换为四元素和旋转矩阵)
Eigen:旋转向量(Angle-Axis)转换为四元素和旋转矩阵
0. 在固定欧拉角系下。 绕固定系旋转,旋转的先后顺序为X、Y、Z。当然也支持XYZ的任意顺序旋转。 1. 转为四元素 Eigen::Quaterniond q Eigen::AngleAxisd(yaw, Eigen::Vector3d::UnitZ()) *Eigen::AngleAxisd(pitch, Eigen::Vector3d::UnitY()) *Eigen::AngleAxi…...

C#8.0本质论第十二章--泛型
C#8.0本质论第十二章–泛型 C#通过泛型来促进代码重用,在词义上等价于C模板。 在泛型编程中,数据类型也是一种参数。 12.1如果C#没有泛型 为object的方法使用值类型时,“运行时”将自动对它进行装箱,获取值类型的实例时则需要…...
自动化打印地图)
Python与ArcGIS系列(七)自动化打印地图
目录 0 简述1 获取可用打印机列表2 打印地图3 导出地图至PDF4 导出地图至图像0 简述 本篇介绍如何利用arcpy实现获取可用打印机列表、打印地图、导出地图至PDF和图像。 1 获取可用打印机列表 通过arcpy提供的ListPrinterNames()函数可以生成可用的打印机列表。 import arcpy.m…...
基于STM32单片机抢答器设计
**单片机设计介绍, 基于STM32单片机抢答器设计-Proteus仿真 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于STM32单片机的抢答器设计可以用于教育和培训场景中的抢答游戏或考试环节。以下是一个基本的介绍设计步骤…...

冯·诺伊曼体系结构--操作系统
文章目录 1.认识冯诺依曼系统1.1约翰冯诺依曼1.2冯诺依曼结构1.3存储器的读写速度1.4对冯诺依曼结构的认识1.5冯诺依曼结构在生活中的演示 2.操作系统--“搞管理”的软件2.1概念2.2OS存在的意义2.3管理的方式2.4系统调用和库函数概念 1.认识冯诺依曼系统 1.1约翰冯诺依曼 1.2冯…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
