postman设置动态token, 每次登录更新token
postman设置动态token, 每次登录更新token
文章目录
- postman设置动态token, 每次登录更新token
- 问题
- 1. 设置全局变量
- 2. 新建登录接口
- 3. 设置脚本
- 4. 切换环境
- 5. 配置动态token
问题
token过期时间一般比较短, 每次使用postman调用接口都token非常麻烦
实现token过期后, 调用一次登录接口, 自动将token更新, 使其他需要token的接口可以正常使用
1. 设置全局变量
新建token全局变量
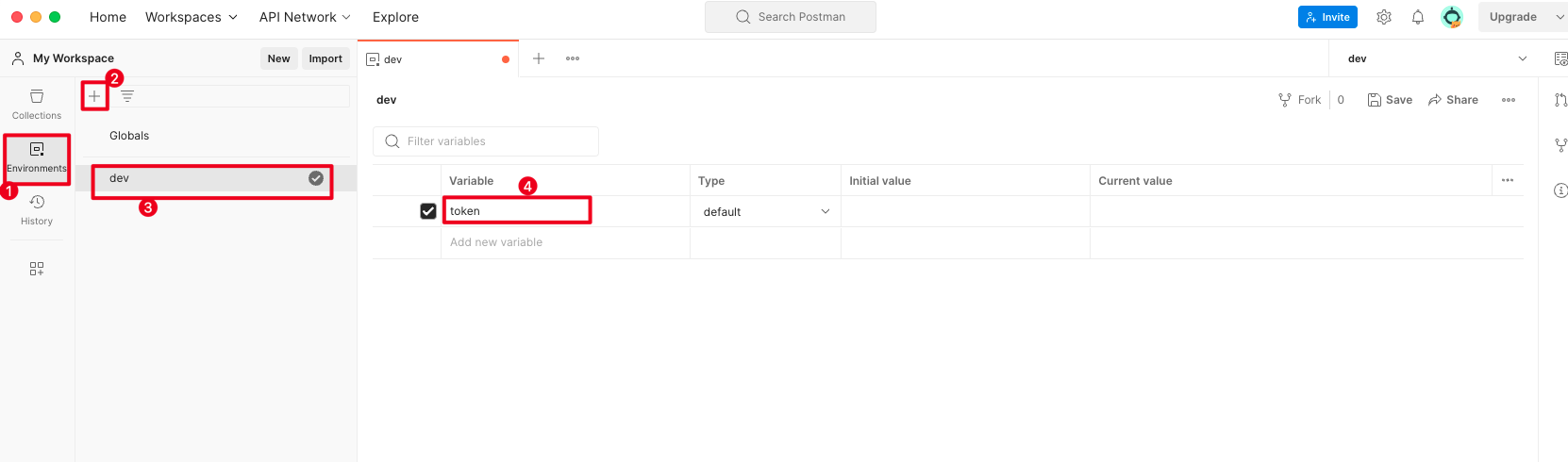
2. 新建登录接口
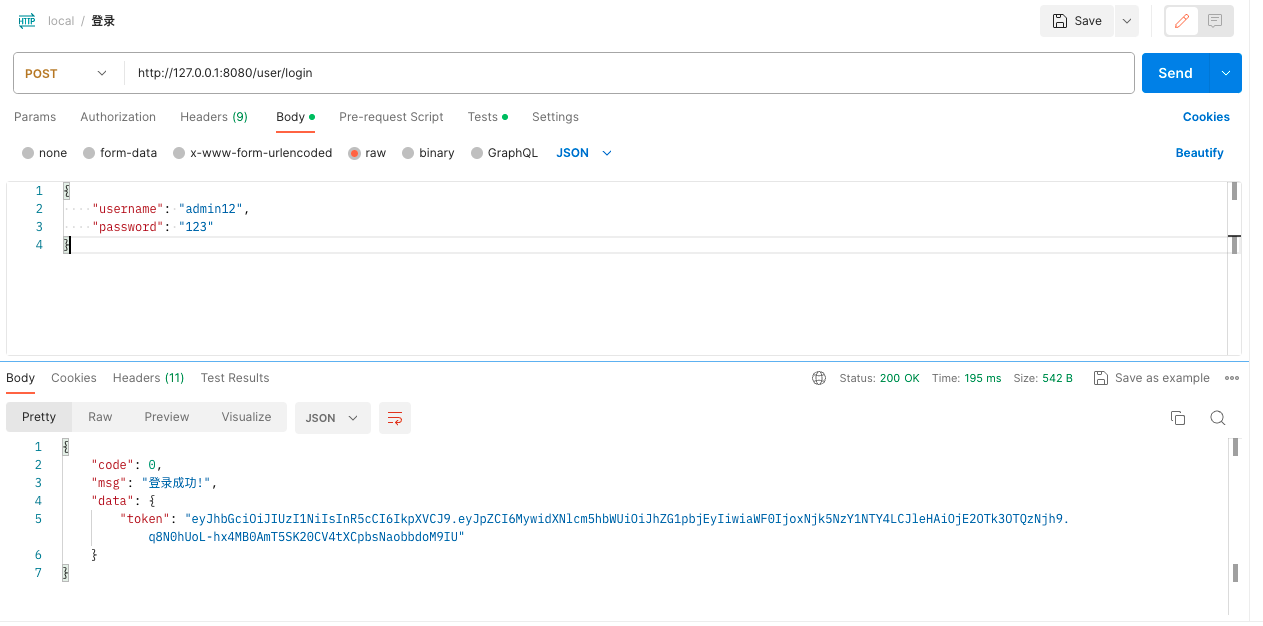
- 返回值
{"code": 0,"msg": "登录成功!","data": {"token": "eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJpZCI6MywidXNlcm5hbWUiOiJhZG1pbjEyIiwiaWF0IjoxNjk5NzY1NTY4LCJleHAiOjE2OTk3OTQzNjh9.q8N0hUoL-hx4MB0AmT5SK20CV4tXCpbsNaobbdoM9IU"}
}
3. 设置脚本
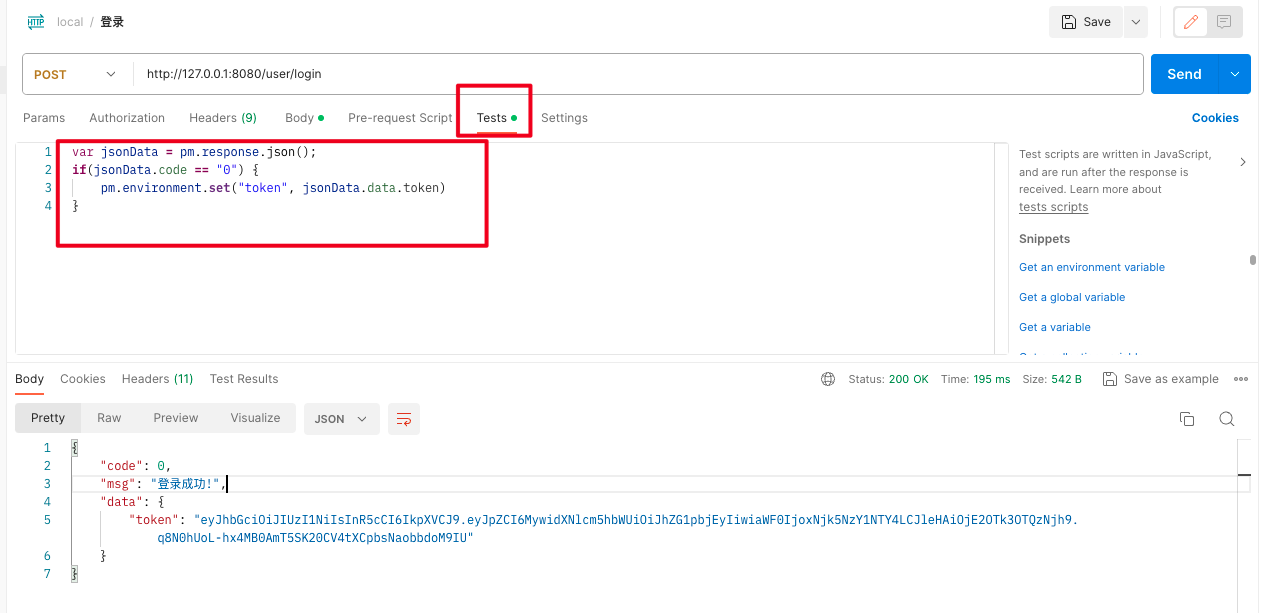
- 脚本
var jsonData = pm.response.json();
// 我的返回值中code为0表示成功
if(jsonData.code == "0") {// 我的返回值token在data.token中pm.environment.set("token", jsonData.data.token)
}
4. 切换环境
- 将环境切换为之前创建的开发环境
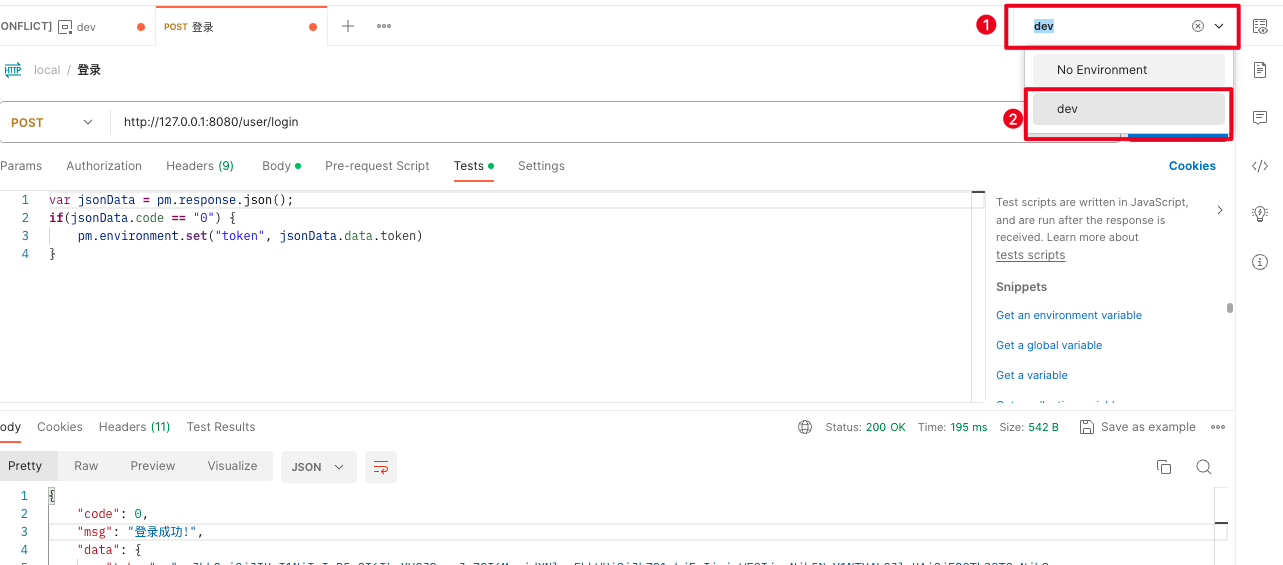
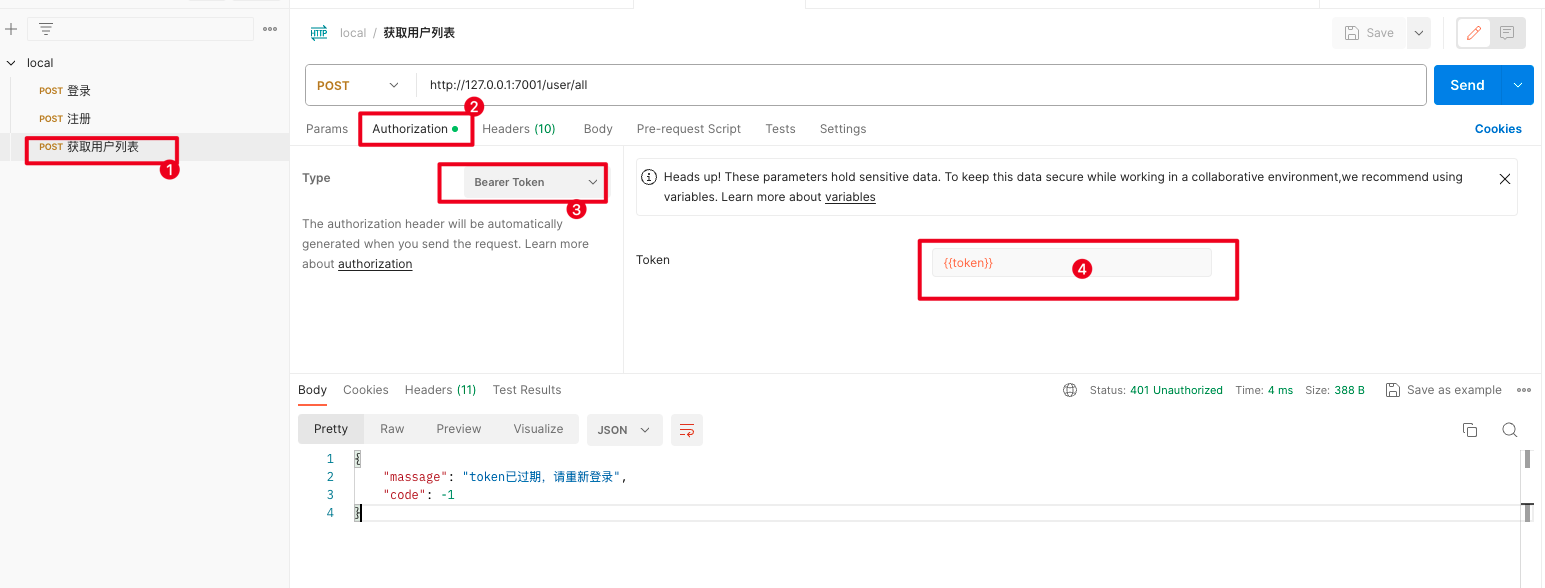
5. 配置动态token
需要token的接口,配置{{token}}
相关文章:

postman设置动态token, 每次登录更新token
postman设置动态token, 每次登录更新token 文章目录 postman设置动态token, 每次登录更新token问题1. 设置全局变量2. 新建登录接口3. 设置脚本4. 切换环境5. 配置动态token 问题 token过期时间一般比较短, 每次使用postman调用接口都token非常麻烦 实现token过期后, 调用一次…...
两篇)
架构师范文(AI写作)两篇
请点击↑关注、收藏,本博客免费为你获取精彩知识分享!有惊喜哟!! 架构师范文-论区块链技术及应用 2022年3月,我参与了某集团内部一款基于区块链技术的数字资产管理平台,该平台是为了方便管理公司旗下的各种…...
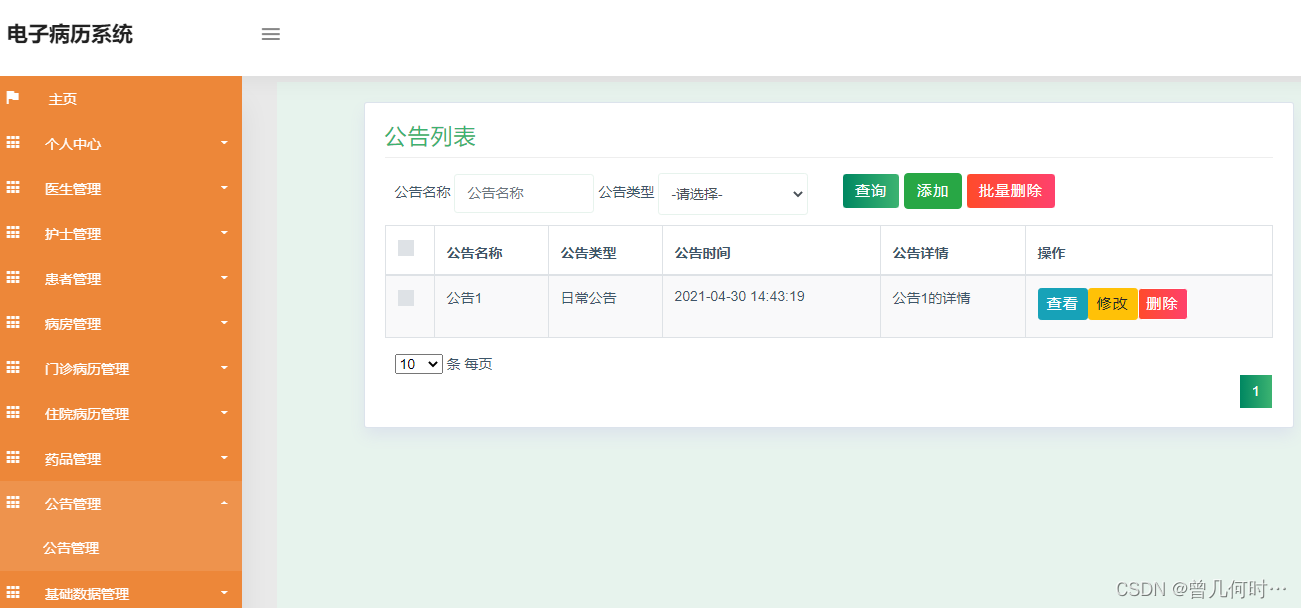
基于SSM的电子病历系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

一次sougo workflow库的使用过程
安装就是常规的make install tutorial http_echoserver实现一下,在macos上实现 cmakelist.txt cmake_minimum_required(VERSION 3.6)set(CMAKE_BUILD_TYPE RelWithDebInfo CACHE STRING "Release")project(mainLANGUAGES C CXX )set(CMAKE_RUNTIME_OUTP…...
macOS Big Sur(macos11版本)
macOS Big Sur是苹果推出的最新操作系统,具有以下特点: 全新的设计风格:Big Sur采用了全新的设计语言,包括更加圆润的窗口和控件、更加鲜明的色彩和更加简洁的界面。这种设计风格使得操作系统更加美观和易用。强大的性能表现&…...
泛微E-Office信息泄露漏洞复现
简介 Weaver E-Office是中国泛微科技(Weaver)公司的一个协同办公系统。 Weaver E-Office 9.5版本存在安全漏洞。攻击者利用该漏洞可以访问文件或目录。 漏洞编号:CVE-2023-2766 漏洞复现 FOFA语法: app"泛微-EOffice&qu…...

-bash: sudo: command not found的解决方法
在 Linux 系统中,使用 sudo 命令时提示 “command not found”,首先执行以下命令看一下 /etc/sudoers.d 文件是否存在: find /etc/sudoers.d1)如果返回 No such file or directory,就说明系统没有安装sudo,…...

CMOS介绍
1 二极管 2 CMOS 2.1 栅极、源极、漏极 2.2 内部结构 2.2 导电原理 - 原理:1.通过门级和衬底加一个垂直电场Ev,从而在两口井之间形成反形层2.如果加的电场足够强,反形层就可以把source(源极)和drain(漏极…...
《软件工程与计算》期末考试真题范例及答案
今天分享一套针对《软件工程与计算》这本书的真题案例,有关《软件工程与计算》23章内容的重点知识整理,已经总结在了博客专栏中,有需要的自行阅读: 《软件工程与计算》啃书总结https://blog.csdn.net/jsl123x/category_12468792.…...
springboot高校全流程考勤系统-计算机毕设 附源码 27637
Springboot高校全流程考勤系统 摘 要 本文针对高校考勤等问题,对其进行研究分析,然后开发设计出高校全流程考勤系统以解决问题。高校全流程考勤系统系统主要功能模块包括:考勤签到、课程信息、考勤情况、申请记录列表等,系统功能设…...

大二第四周总结——用原生js封装一个分页器
用原生js封装一个分页器 起因:这次项目还是用原生的js来写的,我负责的是后台,分页是后台最常见的一个功能了,于是干脆封装一下,废话少说,直接上代码 这里是基本的样式 .pagination {display: flex;width: 600px;hei…...
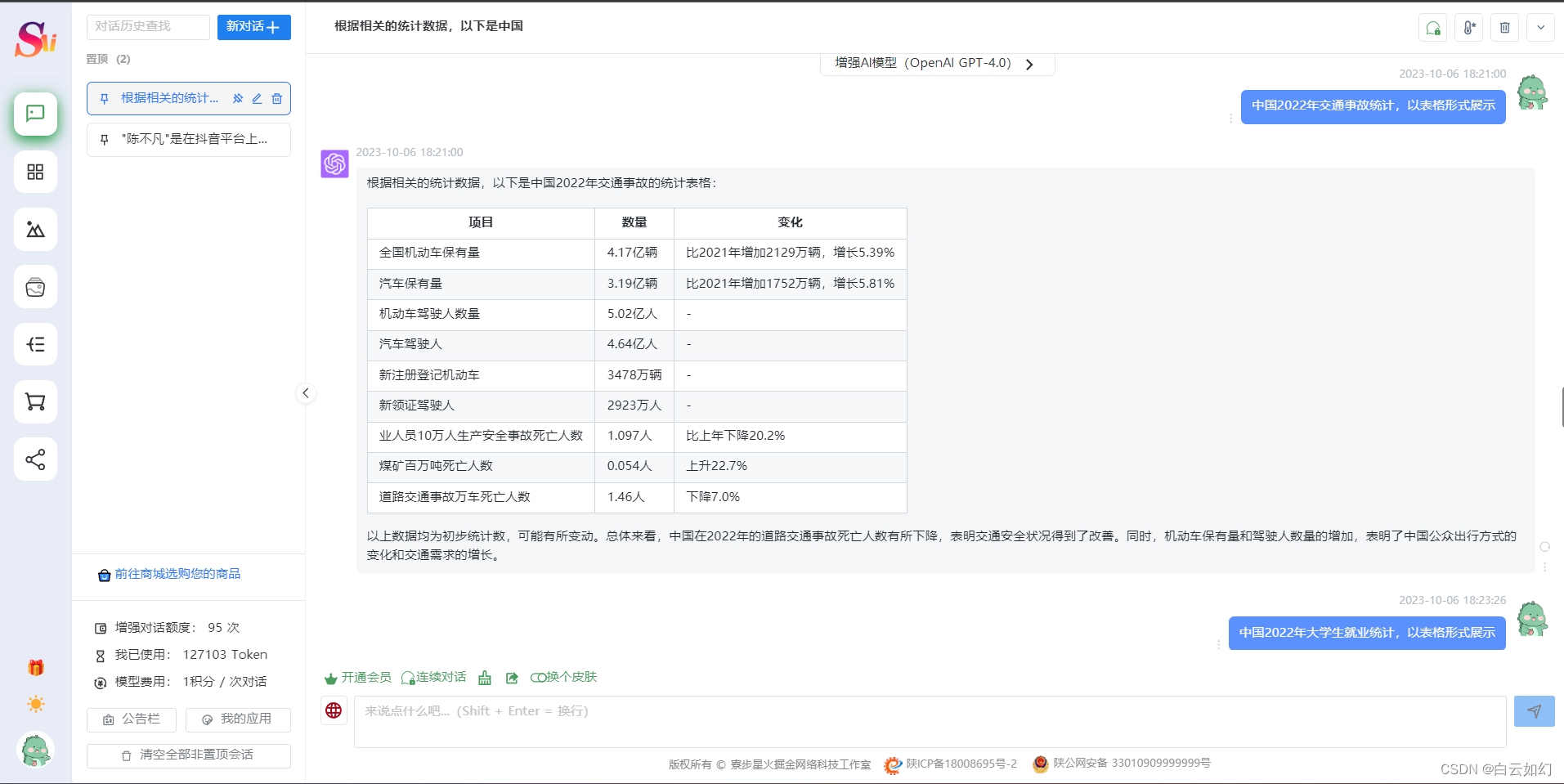
智能AI系统ChatGPT系统源码+支持GPT4.0+支持ai绘画(Midjourney)/支持OpenAI GPT全模型+国内AI全模型
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...
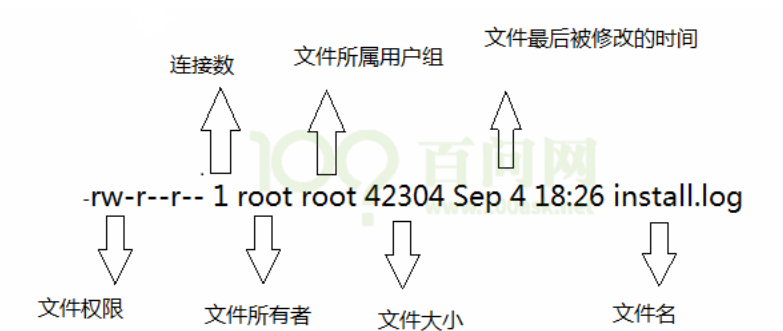
ARM Linux 基础学习 / 系统相关,文件系统,文件属性
编辑整理 by Staok。 本文部分内容摘自 “100ask imx6ull” 开发板的配套资料(如 百问网的《嵌入式Linux应用开发完全手册》,在 百问网 imx6ull pro 开发板 页面 中的《2.1 100ASK_IMX6ULL_PRO:开发板资料》或《2.2 全系列Linux教程…...

nginx https 如何将部分路径转移到 http
nginx https 如何将部分路径转移到 http 我有一个自己的网站,默认是走的 https,其中有一个路径需要走 http。 实现 在 nginx 的配置文件 https 中添加这个路径,并添加一个 rewrite 的指令。 比如我需要将 tools/iphone 的路径转成 http&am…...

算法通关村第八关-白银挑战二叉树的深度和高度问题
大家好我是苏麟 , 今天说说几道二叉树深度和高度相关的题目 . LeetCode给我们造了一堆的题目,研究一下104、110和111三个题,这三个颗看起来挺像的,都是关于深度、高度的。 最大深度问题 描述 : 二叉树的 最大深度 是指从根节点到最远叶子…...

使用LogBack替换Log4j
目录 1.删除log4j有关的依赖,添加logBack依赖 2.删除log4j配置文件,增加logback.xml配置文件 3.更改application.yml配置文件,log文件指向logback.xml 4.重启 1.删除log4j有关的依赖,添加logBack依赖 <dependency><gr…...

财务报告是什么
财务报告是什么 财务报告是企业对外提供的反映企业某一特定日期的财务状况和某一会计期间的经营成果、现金流量等会计信息的文件。 根据财务报告的定义,财务报告具有以下几层含义:一是财务报告应当是对外报告,其服务对象主要是投资者、债权人…...

SOME/IP 协议介绍(四)RPC协议规范
RPC协议规范 本章描述了SOME/IP的RPC协议。 传输协议绑定 为了传输不同传输协议的SOME/IP消息,可以使用多种传输协议。SOME/IP目前支持UDP和TCP。它们的绑定在以下章节中进行了解释,而第[SIP_RPC_450页,第36页]节讨论了选择哪种传输协议。…...

PostgreSQL基础入门
为什么选择PostgreSQL 功能更全面:PGSQL的功能更加全面,支持开窗函数、物化视图、分区表、json等类型,MySQL8以上支持开窗函数、分区表、json等,但物化视图仍不支持。高可用:PG更适合分布式环境,如流复制、…...

Django 密码管理:安全实践与技术深入
在 Web 应用的开发中,密码管理是保障用户安全的关键环节。Django 作为一个强大的 Python Web 框架,提供了一套全面的系统来处理密码的存储、验证和安全。本文将详细探讨 Django 中的密码管理机制,包括密码存储、密码验证、密码安全策略以及自…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...
