进制的转换
1、进制的转化
(1)进制介绍
对于进制,有四种表示方法:
1)二进制:0,1,满2进1,C语言中没有二进制常数的表示方法
2)八进制:0-7,满8进1
3)十进制:0-9,满10进1
4)十六进制:0-9及A-F(A-F分别表示10~15),满16进1.以0X或者0x表示,此处的A-F不区分大小写。
2、进制的转换
(1)进制转换的介绍
第一组(其他进制转换十进制)
1)二进制转十进制
规则:从最低位开始,将每个位上的数提取出来,乘以2的(位数减1)次方,然后求和。
2)八进制转十进制
规则:从最低位开始,将每个位上的数提取出来,乘以8的(位数减1)次方,然后求和。
3)十六进制转十进制
规则:从最低位开始,将每个位上的数提取出来,乘以16的(位数减1)次方,然后求和。
0x34A(16进制)=842(十进制),虽然A在16进制中表示10,但是它植被看做一位,所以0x34A=10*16^(1-1)+4*16^(2-1)+3*16^(3-1)=842。
第二组(十进制转换其他进制)
1)十进制转二进制
规则:将该数不断除2,直到商为0为止,然后将每步得到的余数都倒过来,就是对应的二进制数。
56(十进制)=111000(二进制)
56/2=28...0 28/2=14...0 14/2=7...0 7/2=3...1 3/2=1...0 1/2=0...1
所得余数为000111,他代表的十进制数是1*2^(1-1)+1*2^1+1*2^2=7,将这个余数反过来之后,就变成了111000,他代表的十进制数是1*2^3+1*2^4+1*2^5=56。
这个例子有些特殊,我们看似是把每位取反,实则不然,而是将每一位和其对称的那一位的位置进行了调换。
2)十进制转八进制
规则:将该数不断除8,直到商为0为止,然后将每步得到的余数都倒过来,就是对应的八进制数。
156(十进制)=234(八进制)
156/8=19...4 19/8=2...3 2/8=0...2
所得余数为432,反过来之后就是234,4*8^0+3*8+2*8^2=156。
3)十进制转十六进制
规则:将该数不断除16,直到商为0为止,然后将每步得到的余数都倒过来,就是对应的十六进制数。
356(十进制)=164(十六进制)
356/16=22...4 22/16=1...6 1/16=0...1
所的余数反过来之后就是164,4*16^0+6*16+1*16^2=356。
第三组(二进制转其他进制)
1)二进制转八进制
规则:将二进制每三位一组,缺的位补0,转成对应的十进制数,再把这些十进制数组合起来即可
11010101(二进制)=325(八进制)
先把二进制数每三位一组分开,分别是011、010、101,注意,每组所代表的十进制数分别为3、2、5,所以对应的八进制数就是325了
2)二进制转十六进制
规则:从低位开始,将二进制数每四位一组,转成对应的十进制数,再看这些十进制数有没有大于9的,如果有,转换为对应的16进制即可
11010101(二进制)=
先把二进制数从低到高每四位一组分开分别是1101、0101,他们代表的十进制数是
13、5,13在十六进制中代表的D,所以这个二进制转换成十六进制就是D5。
第四组(其他进制转二进制)
1)八进制转二进制
将八进制每一位,转换成对应的一个三位的二进制数即可
0237(八进制)=000010011111(二进制)=01001111(二进制)
2)十六进制转二进制
将十六进制每一位,转成对应的一个四位的二进制数即可
0x23B(十六进制)=001000111011(二进制)=1000111011(二进制)
相关文章:

进制的转换
1、进制的转化 (1)进制介绍 对于进制,有四种表示方法: 1)二进制:0,1,满2进1,C语言中没有二进制常数的表示方法 2)八进制:0-7,满8进1 3࿰…...

计算机简介
一、是什么 计算机(computer)俗称电脑,是现代一种用于高速计算的电子计算机器,可以进行数值计算,又可以进行逻辑计算,还具有存储记忆功能。是能够按照程序运行,自动、高速处理海量数据的现代化…...
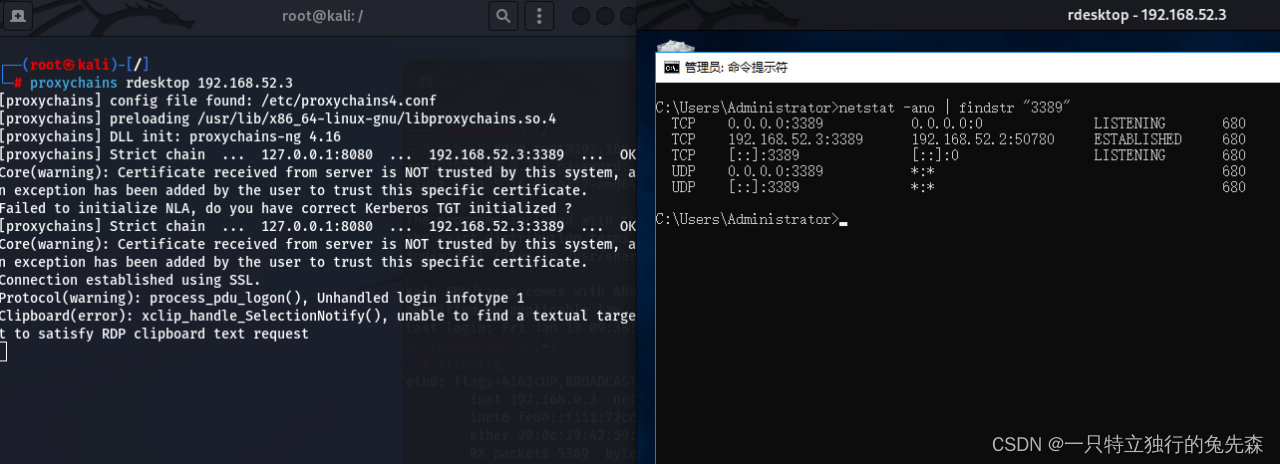
《红蓝攻防对抗实战》十一.内网穿透之利用SSH协议进行隧道穿透
利用DNS协议进行隧道穿透 一.前言二.前文推荐三. 利用SSH协议进行隧道穿透1.SSH隧道-本地端口转发2.SSH隧道-远程端口转发3.SSH隧道-动态端口转发 四.本篇总结 一.前言 SSH(Secure Shell)协议是一种加密的网络传输协议,它可以在不安全的网络…...

工商银行卡安全码怎么看
工商银行的安全码,作为一项至关重要的安全措施,旨在保护用户的银行账户和交易安全。为了查看工商银行的安全码用户需要按照以下步骤操作: 首先,用户需要使用电脑或手机访问工商银行的网上银行平台。在平台首页,用户需要…...
经典的测试开发面试题
1、你在测试中发现了一个bug,但是开发经理认为这不是一个bug,你应该怎样解决? 首先,将问题提交到缺陷管理库进行备案。 然后,要获取判断的依据和标准: 根绝需求说明书,产品说明、设计文档等&…...

win11下安装odoo17(conda python11)
win11下安装odoo17 odoo17发行了,据说,UI做了很大改进,今天有空,体验一下 打开官方仓库: https://github.com/odoo/odoo 默认的版本已经变成17了 打开odoo/odoo/init.py,发现对python版本的要求也提高了…...
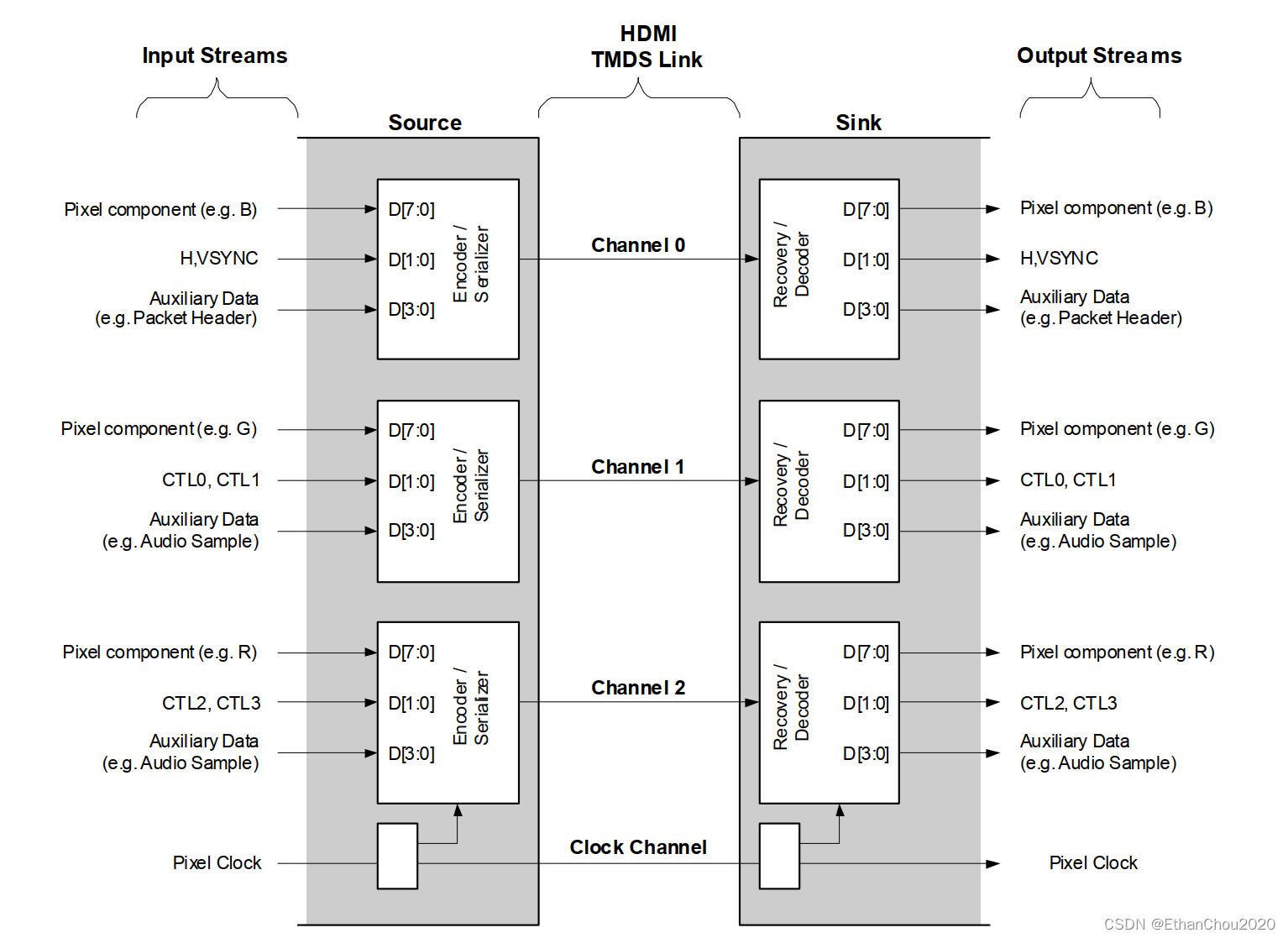
HDMI之编码篇
概述 HDMI 2.0b(含)以下版本,采用3个Channel方式输出。传输又分为3三种周期,视频数据,数据岛以及控制周期。视频传输采用8/10编码。数据岛采用4/10编码(TERC4)。控制周期采用2/10。编码都拓展成了10bits。 上图中,Pixel component(e.g.B)->D[7:0]表示视频数据周期…...

关于DataLoader是否shuffle在VOC2007语义分割数据集上引发的问题
问题描述: 在训练过程中,训练集和验证集实时得到的F1分数相差很大,如下图: 这个问题之前从未遇到过,后来经过不断的排查,发现是因为验证集的数据加载器中shuffle设置的为False,而训练集设置的为…...

在以TAB为首地址的字存储区中存放有N个无符号数,试统计低3位全为1的数的个数(个数设为≤9),并显示。
;默认认采用ML6.11汇编程序 DATAS SEGMENT;此处输入数据段代码TAB DW -7,7,15,20,21N($-TAB)/2;G DW 0 DATAS ENDS STACKS SEGMENT;此处处输入堆栈段代码; DB 200 DUP(0) STACKS ENDS CODES SEGMENTASSUME CS:CODES,DS: DATAS, SS:STACKS START:MOV AX, DATASMOV DS,AX;此处输入…...
和输出print(),及经验用法)
python的输入input()和输出print(),及经验用法
python的输入和输出有什么用呢 各位,举个例子,在web应用当中,很多的用于与用户进行交互的输入输出大都是交给web前端的,尤其是交给javascript来完成,不仅简单、方便,而且能够减轻数据在服务器端与客户端之…...

Docker实现挂载的N种方式
目录 docker挂载实现挂载的方式绑定挂载数据卷(Volume)挂载DockerFile 定义数据卷临时文件系统(tmpfs)挂载挂载 docker挂载 默认情况下,在Docker容器内创建的所有文件都只能在容器内部使用。容器删除后,数…...

【使用python写一段代码将pdf文件转换为word文件】
突然有一个需求 就是将一份老板发的PDF文件,转换为Word文档,发现要么收费,要么就是有水印,更有甚者需要将转换收费(美其名曰就是需要开会员),那能惯着他吗 开整! 1.使用python写一段…...

人工智能基础——图像认知与OpenCV
人工智能的学习之路非常漫长,不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心,我为大家整理了一份600多G的学习资源,基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得…...
docker-compose安装es以及ik分词同义词插件
目录 1 前言 2 集成利器Docker 2.1 Docker环境安装 2.1.1 环境检查 2.1.2 在线安装 2.1.3 离线安装 2.2 Docker-Compose的安装 2.2.1 概念简介 2.2.2 安装步骤 2.2.2.1 二进制文件安装 2.2.2.2 离线安装 2.2.2.3 yum安装 3 一键安装ES及Kibana 3.1 yml文件的编写…...
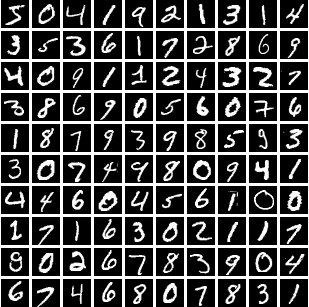
【matlab】KMeans KMeans++实现手写数字聚类
目录 matlab代码kmeans matlab代码kmeans MNIST DATABASE下载网址: http://yann.lecun.com/exdb/mnist/ 聚类 将物理或抽象对象的集合分成由类似特征组成的多个类的过程称为聚类(clustering)。 对于给定N个n维向量x1,…,xN∈Rn,聚类的目标…...

从系统层到应用层,vivo 已在安全生态层
你每隔多久就会使用一次手机?调研结果也许会让你大吃一惊。 权威报告数据显示,2022年,24.9%的受访者每日使用手机时长超过10小时,其中3.8%的受访者“机不离手”,每日使用时长超过15小时。而真正让手机化身为时间吞金兽…...
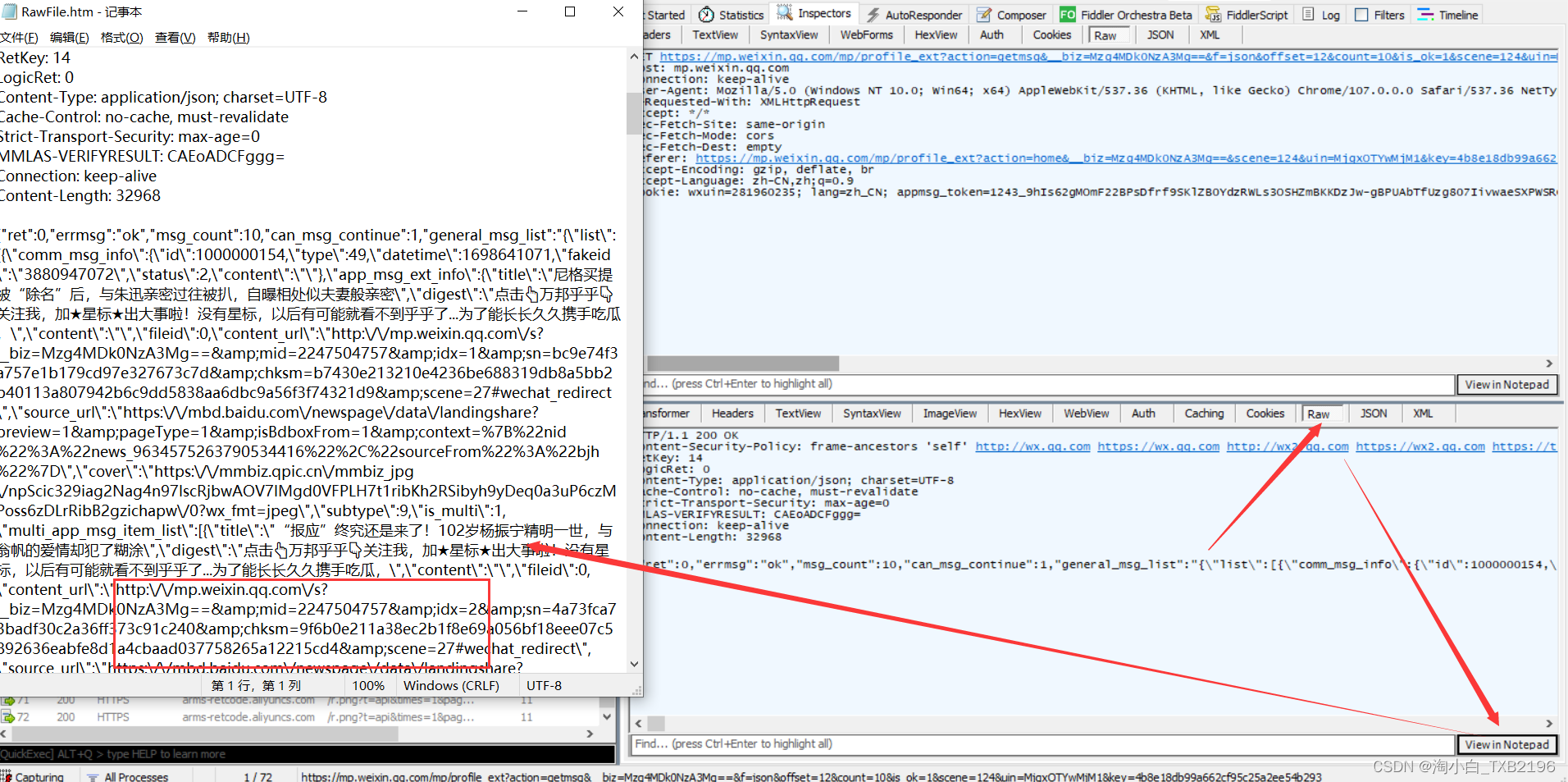
微信公众号历史文章采集教程思路
大家好,我是淘小白! 今天来说下微信公众号历史记录文章采集的教程和思路,希望能够帮助的到大家~ 1、历史消息入口 现在新版本的微信已经找不到历史记录的入口了,需要对这个入口进行拼接,方法如下: 随便…...

大模型应用--prompt工程实践
在使用大模型进行prompt 训练时,自己做的相关笔记。 本文以openai<1.0版为例。 1.调用大模型 定义调用openai大模型的函数 get_completion() def get_completion(prompt, model"gpt-3.5-turbo"):messages [{"role": "user", …...
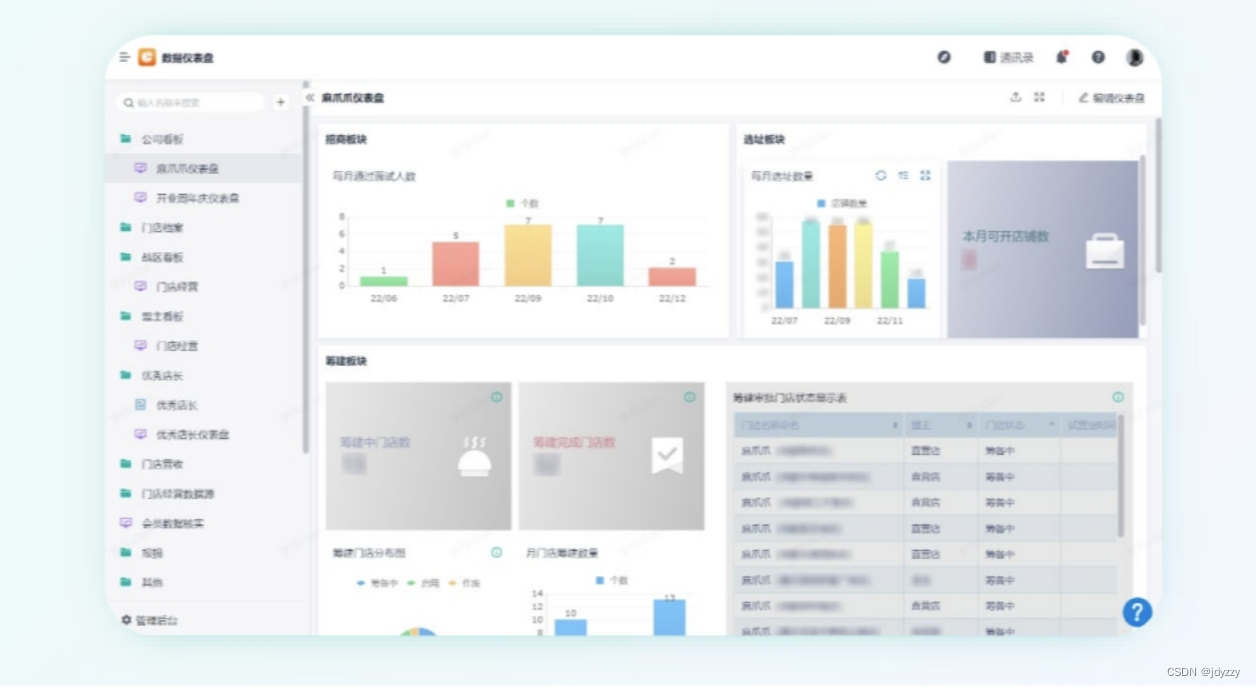
新零售时代,传统便利店如何转型?
在零售批发业,如何降低各环节成本、提高业务运转效率、更科学地了解客户服务客户,是每家企业在激烈竞争中需要思考的课题。 对零售批发企业来说,这些问题或许由来已久: (1)如何对各岗位的员工进行科学的考…...
openEuler 系统使用 Docker Compose 容器化部署 Redis Cluster 集群
openEuler 系统使用 Docker Compose 容器化部署 Redis Cluster 集群 Redis 的多种模式Redis-Alone 单机模式Redis 单机模式的优缺点 Redis 高可用集群模式Redis-Master/Slaver 主从模式Redis-Master/Slaver 哨兵模式哨兵模式监控的原理Redis 节点主客观下线标记Redis 节点主客观…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
