数据分析实战 | 泊松回归——航班数据分析
目录
一、数据及分析对象
二、目的及分析任务
三、方法及工具
四、数据读入
五、数据理解
六、数据准备
七、模型训练
八、模型评价
一、数据及分析对象
CSV文件:o-ring-erosion-only.csv
数据集链接:https://download.csdn.net/download/m0_70452407/88524654
该数据集给出了挑战者航天飞机的O型圈(O-Ring)数据,主要属性如下:
(1)Number of O-ring at risk on a given flight:航班上存在潜在风险的O形环数量。
(2)Number experiencing thermal distress:出现热损伤的O形环数量。
(3)Launch temperature(degrees F):发射温度(华氏度)。
(4)Leak-check pressure(psi):捡漏压力(psi)。
(5)Temporal order of flight:航班时序。
二、目的及分析任务
理解机器学习方法在数据分析中的应用——采用泊松回归方法进行回归分析。
(1)以全部记录为训练集进行泊松回归建模。
(2)对模型进行假设检验和可视化处理,验证泊松回归建模的有效性。
三、方法及工具
Python语言及其第三方包pandas、NumPy和statsmodels
四、数据读入
由于原数据没有表头,因此在读取CSV文件时通过names参数手动生成表头。
import pandas as pd
df_erosion=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第3章 回归分析\\o-ring-erosion-only.csv",names=['Number of O-ring at risk on a given flight','Number experiencing thermal distress','Launch temperature(degrees F)','Leak-check pressure(psi)','Temporal order of flight'])df_erosion.head()
五、数据理解
对数据框df_erosion进行探索性分析:
df_erosion.describe()
其中,预测变量"Number experiencing thermal distress"的最大值为2,最小值为0,平均热损伤O形环数为0.391。
除了describe()方法,还可以调用shape属性和columns属性对数据框进行探索性分析。
df_erosion.shape(23, 5)
df_erosion.columnsIndex(['Number of O-ring at risk on a given flight','Number experiencing thermal distress', 'Launch temperature(degrees F)','Leak-check pressure(psi)', 'Temporal order of flight'],dtype='object')
绘制直方图来查看因变量“Number experiencing thermal distress”数据的连续性,通过调用mayplotlib.pyplot包中数据框(DataFrame)的hist()方法创建频数直方图。
import matplotlib.pyplot as plt
plt.rcParams['font.family']="simHei" #汉字显示 字体设置
plt.hist(df_erosion['Number experiencing thermal distress'],bins=10,facecolor="blue",edgecolor="black",alpha=0.7)
plt.xlabel('区间')
plt.ylabel('频数')
plt.title("因变量‘Number experiencing thermal distress’频数分布直方图")
通过调用NumPy包中数据框(DataFrame)的mean()方法和var()方法查看因变量“Number experiencing thermal distress”的均值和方差。
import numpy as np
print(np.mean(df_erosion['Number experiencing thermal distress']))
print(np.var(df_erosion['Number experiencing thermal distress']))0.391304347826087 0.41209829867674863
可以看到方差约等于平均值,避免了在泊松分布中发生过度分散或分散不足的情况。泊松分布的一个重要特征是均值和方差相等,称为分散均衡。只有分散均衡的数据才能使用泊松分布模型。均值小于方差称为分散过度,所有分布向左侧倾斜,数值较小的数据出现概率较高。均值大于方差的称为分散不足。
六、数据准备
进行泊松回归分析前,应准备好模型所需的特征矩阵(X)和目标向量(y)。这里采用Python的统计分析包statsmodels进行自动你类型转换,数据对象y即可使用。若采用其他包(如scikit-learn等需要采用np.ravel()方法对y进行转换)。
原始数据集中列名过长,需要对其重新命名。同时遵从习惯调整特征顺序,将因变量调至最后一列。
df_erosion.rename(columns={'Number of O-ring at risk on a given flight':'num_rings','Launch temperature(degrees F)':'temperature','Leak-check pressure(psi)':'pressure','Number experiencing thermal distress':'num_distress','Temporal order of flight':'order'},inplace=True)
order=['num_rings','temperature','pressure','order','num_distress']
df_erosion=df_erosion[order]df_erosion.head()
七、模型训练
以航班上存在潜在风险的O形环数量num_rings、发射温度temperature、捡漏压力pressure和航班时许order作为自变量,飞行中热损伤O形环的数量num_distress作为因变量对数据进行泊松回归建模。这里采用的实现方式为调用Python的统计分析包statsmodels中的GLM()方法进行建模分析。
import statsmodels.formula.api as smfstatsmodels.GLM()方法的输入有3个,第一个形参为formula,具体形式为y~x,在这里即为“num_distress~num_rings+temperature+pressure+order"。第二个参数是模型训练所用的数据集df_erosion。最后一个参数为创建GLM模型所用的Poisson()模型。这里通过调用NumPy库的column_stack()方法对各自变量矩阵按列合并创建特征矩阵X。
x=np.column_stack((df_erosion['num_rings'],df_erosion['temperature'],df_erosion['pressure'],df_erosion['order']))在自变量x和因变量y上使用GLM()方法进行泊松回归。
import statsmodels.api as sm
glm=smf.glm('num_distress~num_rings+temperature+pressure+order',df_erosion,family=sm.families.Poisson())然后获取拟合结果,并将回归拟合的摘要全部打印出来。
results=glm.fit()
print(results.summary())Generalized Linear Model Regression Results ============================================================================== Dep. Variable: num_distress No. Observations: 23 Model: GLM Df Residuals: 19 Model Family: Poisson Df Model: 3 Link Function: Log Scale: 1.0000 Method: IRLS Log-Likelihood: -15.317 Date: Sat, 11 Nov 2023 Deviance: 15.407 Time: 12:45:43 Pearson chi2: 23.4 No. Iterations: 5 Pseudo R-squ. (CS): 0.2633 Covariance Type: nonrobust ===============================================================================coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------- Intercept 0.0984 0.090 1.094 0.274 -0.078 0.275 num_rings 0.5905 0.540 1.094 0.274 -0.468 1.649 temperature -0.0883 0.042 -2.092 0.036 -0.171 -0.006 pressure 0.0070 0.010 0.708 0.479 -0.012 0.026 order 0.0115 0.077 0.150 0.881 -0.138 0.161 ===============================================================================
第二部分的coef列所对应的Intercept、num_rings、temperature、pressure和order就是计算出的回归模型中各自变量的系数。
除了读取回归摘要外,还可以调用params属性查看拟合结果。
results.paramsIntercept 0.098418 num_rings 0.590510 temperature -0.088329 pressure 0.007007 order 0.011480 dtype: float64
八、模型评价
通过模型摘要可以看到,只有自变量temperature的p值小于0.05,通过了T检验。这意味着其他解释变量在控制temperature的前提下,对因变量的影响不显著。
建立的泊松回归模型如下:
模型的预测结果如下:
df_erosion['predict_result']=results.predict(df_erosion)
df_erosion['predict_result']=df_erosion['predict_result'].apply(lambda x:round(x,3))df_erosion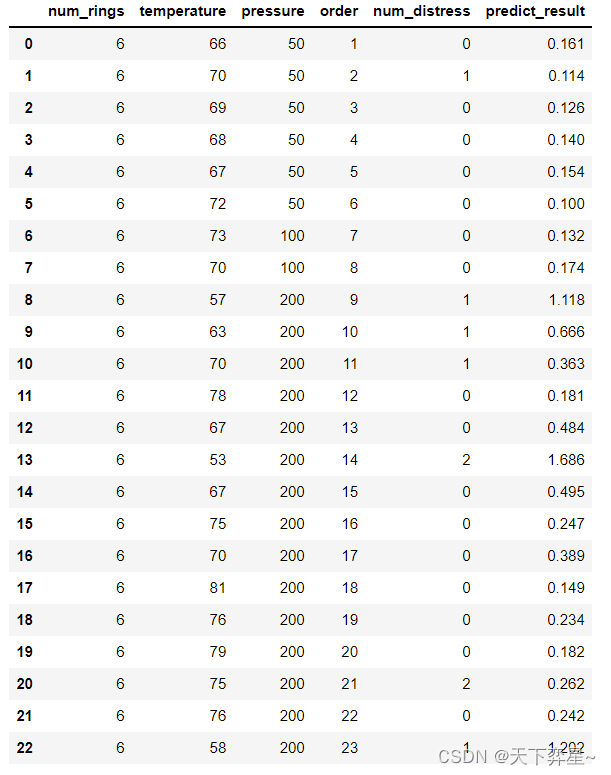
最后采用均方根误差(RMSE)来评估模型预测结果。
from sklearn.metrics import mean_squared_error
print("RMSE:",np.sqrt(mean_squared_error(df_erosion.predict_result,df_erosion.num_distress)))RMSE: 0.4895481057323038
此结果说明该模型的均方根误差为0.490,表明该模型有一定的预测能力。
相关文章:

数据分析实战 | 泊松回归——航班数据分析
目录 一、数据及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 八、模型评价 一、数据及分析对象 CSV文件:o-ring-erosion-only.csv 数据集链接:https://download.csdn.net/download/m0_7…...

Fliki AI:让视频创作更简单、更高效
在当今的数字时代,视频已经成为人们获取信息和娱乐的重要方式。无论是企业宣传、教育培训还是个人创作,视频都发挥着越来越重要的作用。然而,视频制作是一项复杂的工作,需要掌握一定的技能和经验。这对于初学者或没有专业视频制作…...

webGL编程指南 第五章 MultiTexture.html
我会持续更新关于wegl的编程指南中的代码。 当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助 git代码地址 :空 上一章节中我们学习texParameteri的使用,这一章节中我们两个图片进行混合 <!DOCTYPE html> <htm…...

mysql8安装和驱动jar包下载
方式一:基于docker安装 下拉镜像 docker pull mysql:8.0.21 启动镜像 docker run -p 3307:3306 --name mysql -e MYSQL_ROOT_PASSWORDhadoop -d mysql:8.0.21 启动成功后,进入容器内部拷贝配置文件,到宿主主机 docker cp mysql:/etc/mysql…...

(SpringBoot)第五章:SpringBoot创建和使用
文章目录 一:Spring和SpringBoot(1)Spring已解决和未解决的问题(2)SpringBoot 二:Spring项目的创建(1)IDEA创建(2)网页端创建 三:项目目录介绍及运…...
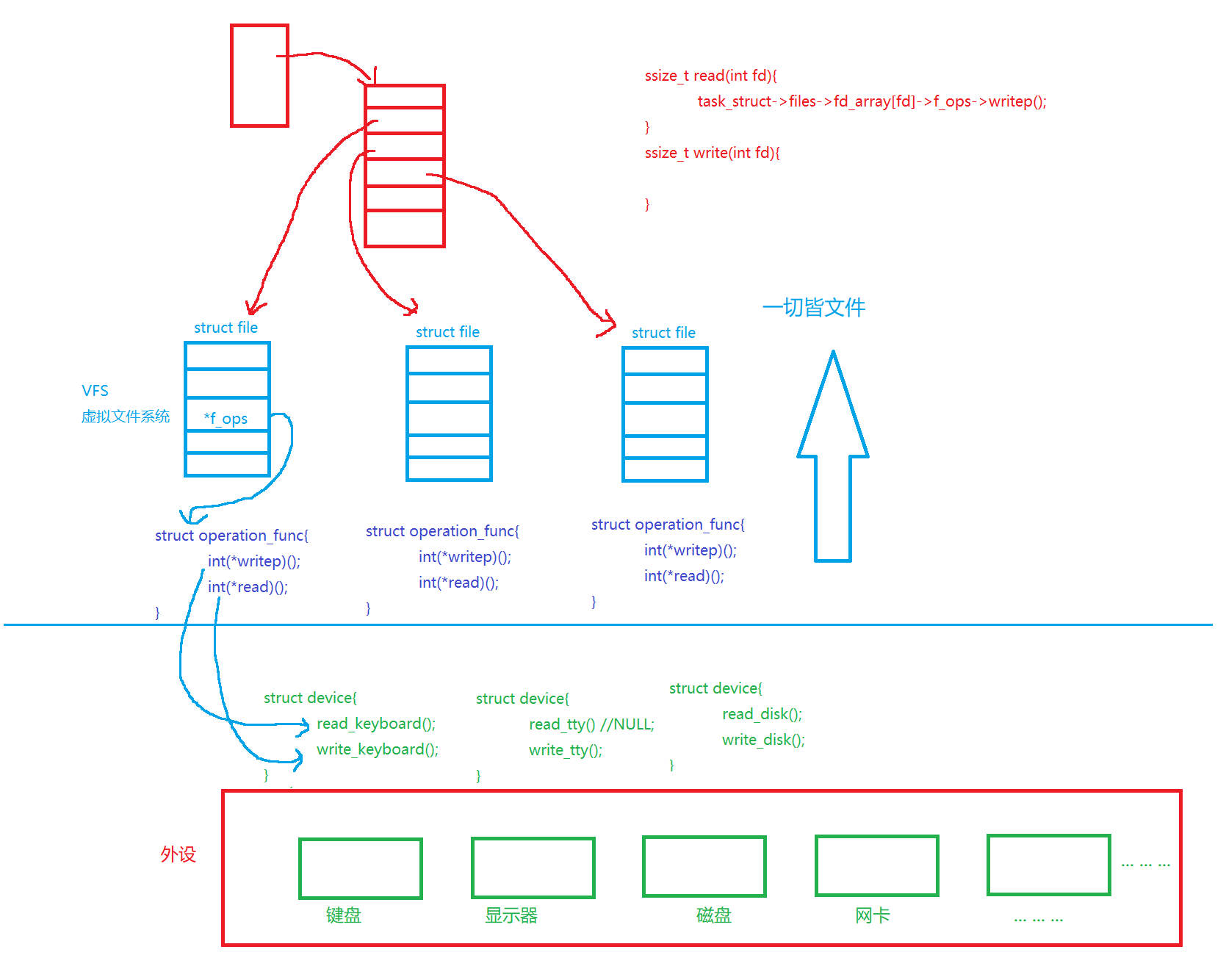
Linux重定向
文章目录 1. 文件描述符分配规则2. 重定向接口dup2自定义shell重定向(补充) 3. 标准输出和标准错误4. 如何理解一切接文件 本章代码gitee地址:文件重定向 1. 文件描述符分配规则 文件描述符的分配规则是从0下标开始,寻址最小的没有使用的数组位置&#…...

Python之文件与文件夹操作及 pytest 测试习题
目录 1、文本文件读写基础。编写程序,在 当前目录下创建一个文本文件 test.txt,并向其中写入字符串 hello world。2、编写一个程序 demo.py,要求运行该程序后,生成 demo_new.py 文件,其中内容与demo.py 一样࿰…...

物联网:实现数据驱动决策,推动经济发展
开发物联网系统的意义主要体现在以下几个方面: 连接一切:物联网的目标是连接一切,将生活中的各种物理对象互联起来。通过物联网开发,我们可以实现各类设备的智能化,包括家居设备、交通工具、工业设备等。这将为人们提…...

Leetcode 2929. Distribute Candies Among Children II
Leetcode 2929. Distribute Candies Among Children II 1. 解题思路2. 代码实现 题目链接:2929. Distribute Candies Among Children II 1. 解题思路 这一题很惭愧,没能自力搞定,最后是看了大佬的思路之后才做出来的,唉…… 这…...

【面经】ES中分片是什么?副本是什么?
ES分片 分片是将一个索引切分为多个底层物理的Lucene索引,这些被切分出来的每个部分称为一个分片。 每个分片都是一个全功能且独立的索引,可由集群中的任何主机存储。 在创建索引时,用户可以指定其分片的数量。 默认情况下,每个索…...

【算法练习Day46】判断子序列不同的子序列
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 判断子序列不同的子序列总结…...

Java设计模式之访问者模式
目录 定义 结构 案例 优点 缺点 使用场景 扩展 分派 案例实现须知 动态分派 静态分派 双分派 定义 封装一些作用于某种数据结构中的各元素的操作,它可以在不改变这个数据结构的前提下定义作用于这些元素的新的操作。 结构 访问者模式包含以下主要角色…...

PySide/PYQT如何用Qt Designer和代码来设置文字属性,如何设置文字颜色?
文章目录 📖 介绍 📖🏡 环境 🏡📒 实现方法 📒📝 Qt Designer设置📝 代码📖 介绍 📖 本人介绍如何使用Qt Designer/代码来设置字体属性(包含字体颜色) 🏡 环境 🏡 本文使用Pyside6来进行演示📒 实现方法 📒 📝 Qt Designer设置 首先打开Qt De…...

ubuntu 设置最大带宽
背景 近日做实验,需要限制一些机子的带宽以达到模拟的效果。在网上搜索了一阵子,结合自己实操的经验,潦草写下这篇文章,供自己与有需要的人参考。 环境: Ubuntu 22.04.1 LTS 安装 wondershaper 和 speedtest-cli w…...

如何在 Python 中执行 MySQL 结果限制和分页查询
Python MySQL 限制结果 限制结果数量 示例 1: 获取您自己的 Python 服务器 选择 “customers” 表中的前 5 条记录: import mysql.connectormydb mysql.connector.connect(host"localhost",user"您的用户名",password"您的密码"…...
Django配置文件,request,链接mysql方法,Orm简介
三板斧问题(views.py) HttpResponse # 返回的是字符串render # 渲染一个HTML静态文件,模板文件redirect # 重定向的 在视图文件中得视图函数必须要接收一个形参request,并且,视图函数也要有返回值ÿ…...

ubuntu下载各个版本chrome方法
Ubuntu/debian 在这里面找版本 https://unix.stackexchange.com/a/612981然后添充进去 http://dl.google.com/linux/chrome/deb/pool/main/g/google-chrome-stable/google-chrome-stable_[HERE_THE_FULL_VERSION]_amd64.deb比如:https://dl.google.com/linux/chro…...

Http状态码502常见原因及排错思路(实战)
Http状态码502常见原因及排错思路 502表示Bad Gateway。当Nginx返回502错误时,通常表示Nginx作为代理服务器无法从上游服务器(如:我们的后端服务器地址)获取有效的响应。导致这种情况的原因有很多: 后端服务器故障ngin…...
国际阿里云:无法ping通ECS实例公网IP的排查方法!!!
无法ping通ECS实例的原因较多,您可以参考本文进行排查。 问题现象 本地客户端无法ping通目标ECS实例公网IP,例如: 本地客户端为Linux系统,ping目标ECS实例公网IP时无响应,如下所示: 本地客户端为Windo…...

Nginx缓存基础
1 nginx缓存的流程 客户端需要访问服务器的数据时,如果都直接向服务器发送请求,服务器接收过多的请求,压力会比较大,也比较耗时;而如果在nginx缓存一定的数据,使客户端向基于nginx的代理服务器发送请求&…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
