线性判别分析(Linear Discriminant Analysis,LDA)
Linear Discriminant Analysis(LDA)
输入:
原始数据$D=((x_1,y_1),(x_2,y_2),...,(x_m,y_m)$ 、 类别标签$Y=[y_1,y_2,...,y_n]$、 降维到的维度d
输出:
投影矩阵W、投影后的样本$Z$、
算法步骤:
- 1.计算类内散度矩阵 S w S_w Sw
- 2.计算类间散度矩阵 S b S_b Sb
- 3.计算矩阵 S w − 1 S b S_w^{-1}S_b Sw−1Sb
- 4.计算 S w − 1 S b S_w^{-1}S_b Sw−1Sb的最大的d个特征值和对应的d个特征向量 ( w 1 , w 2 , . . . , w d ) (w_1,w_2,...,w_d) (w1,w2,...,wd)得到投影矩阵W
- 5.对样本集中的每一个样本特征 x i x_i xi,转换为新的样本 z i = W T x i z_i=W^Tx_i zi=WTxi
- 6.得到输出样本集 D ′ = ( ( z 1 , y 1 ) , ( z 2 , y 2 ) , . . . , ( z m , y m ) ) D'= ((z_1,y_1),(z_2,y_2),...,(z_m,y_m)) D′=((z1,y1),(z2,y2),...,(zm,ym))
二类LDA
对于两个类别的中心点 μ 0 , μ 1 μ_0,μ_1 μ0,μ1,在直线 w w w的投影为 w T μ 0 w^Tμ_0 wTμ0和 w T μ 1 w^Tμ_1 wTμ1。
- 让不同类别的数据的类别中心之间的距离尽可能的大,也就是我们要最大化 ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 ||w^Tμ_0−w^Tμ_1||_2^2 ∣∣wTμ0−wTμ1∣∣22
- 希望同一种类别数据的投影点尽可能的接近 Σ x ∈ w i ( w T x − w T μ i ) 2 Σ_{x∈w_i}(w^Tx-w^Tμ_i)^2 Σx∈wi(wTx−wTμi)2尽可能小,也就是要同类样本投影点的协方差 w T Σ 0 w 和 w T Σ 1 w w^TΣ_0w和w^TΣ_1w wTΣ0w和wTΣ1w尽可能的小,即最小化 w T Σ 0 w + w T Σ 1 w w^TΣ_0w+w^TΣ_1w wTΣ0w+wTΣ1w。
优化的目标函数:
J ( w ) = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T Σ 0 w + w T Σ 1 w = w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w w T ( Σ 0 + Σ 1 ) w J(w)=\frac{||w^Tμ_0-w^Tμ_1||_2^2}{w^TΣ_0w+w^TΣ_1w} =\frac{w^T(μ_0-μ_1)(μ_0-μ_1)^Tw}{w^T(Σ_0+Σ_1)w}\\ J(w)=wTΣ0w+wTΣ1w∣∣wTμ0−wTμ1∣∣22=wT(Σ0+Σ1)wwT(μ0−μ1)(μ0−μ1)Tw
定义类内散度矩阵:
S w = Σ 0 + Σ 1 = ∑ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ X 1 ( x − μ 1 ) ( x − μ 1 ) T \\ S_w =Σ_0+Σ_1\\ =∑_{x∈X_0}(x−μ_0)(x−μ_0)^T+∑_{x∈X_1}(x−μ_1)(x−μ_1)^T\\ Sw=Σ0+Σ1=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T
定义类间散度矩阵:
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b=(μ_0−μ_1)(μ_0−μ_1)^T Sb=(μ0−μ1)(μ0−μ1)T
对此目标函数的优化:
J ( w ) = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T Σ 0 w + w T Σ 1 w = w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w w T ( Σ 0 + Σ 1 ) w J(w)=\frac{||w^Tμ_0-w^Tμ_1||_2^2}{w^TΣ_0w+w^TΣ_1w} =\frac{w^T(μ_0-μ_1)(μ_0-μ_1)^Tw}{w^T(Σ_0+Σ_1)w}\\ J(w)=wTΣ0w+wTΣ1w∣∣wTμ0−wTμ1∣∣22=wT(Σ0+Σ1)wwT(μ0−μ1)(μ0−μ1)Tw
方法一:使用拉格朗日乘子法
可以将分母进行归一化:如果分子分母都可以任意取值那将会有无穷解,故将分母限制长度为1。
此时:
{ J ( w ) = w T S b w w T S w w s . t . w T S w w = 1 \begin{cases} J(w) =\frac{w^TS_bw}{w^TS_ww}\\ s.t.\ w^TS_ww = 1 \end{cases} {J(w)=wTSwwwTSbws.t. wTSww=1
使用拉格朗日乘子法:
c ( w ) = w T S b w − λ ( w T S w w − 1 ) → d c ( w ) d w = 2 S b w − 2 λ S w w = 0 → S b w = λ S w w → S w − 1 S b w = λ w c(w) = w^TS_bw - \lambda(w^TS_ww-1)\\ →\frac{dc(w)}{dw}=2S_bw-2\lambda S_ww = 0\\ →S_bw = \lambda S_ww\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ →S_w^{-1}S_bw=\lambda w\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ c(w)=wTSbw−λ(wTSww−1)→dwdc(w)=2Sbw−2λSww=0→Sbw=λSww →Sw−1Sbw=λw
由上式得:求解的w就是矩阵 S w − 1 S b S_w^{-1}S_b Sw−1Sb的特征向量
方法二:使用瑞利商的结论
瑞利商是指这样的函数
R ( A , x ) = x H A x x H x R(A,x)=\frac{x^HAx}{x^Hx} R(A,x)=xHxxHAx
它有性质:
它的最大值等于矩阵A最大的特征值,而最小值等于矩阵A的最小的特征值,也就是满足 λ m i n ≤ x H A x x H x ≤ λ m a x λ_{min}≤\frac{x^HAx}{x^Hx}≤λ_{max} λmin≤xHxxHAx≤λmax
广义瑞利商。广义瑞利商是指这样的函数 R ( A , B , x ) R(A,B,x) R(A,B,x):
R ( A , x ) = x H A x x H B x R(A,x)=\frac{x^HAx}{x^HBx} R(A,x)=xHBxxHAx
我们令 x = B − 1 / 2 x ′ x=B−1/2x′ x=B−1/2x′,则分母转化为: x H B x = x ′ H ( B − 1 2 ) H B B − 1 2 x ′ = x ′ H B − 1 2 B B − 1 2 x ′ = x ′ H x ′ x^HBx=x′H(B^{\frac{−1}2})^HBB^{\frac{−1}2}x′=x′^HB^{\frac{−1}2}BB^{\frac{−1}2}x′=x′^Hx′ xHBx=x′H(B2−1)HBB2−1x′=x′HB2−1BB2−1x′=x′Hx′
而分子转化为:
x H A x = x ′ H B − 1 / 2 A B − 1 / 2 x ′ x^HAx=x′^HB^{−1/2}AB^{−1/2}x′ xHAx=x′HB−1/2AB−1/2x′
此时我们的 R ( A , B , x ) R(A,B,x) R(A,B,x)转化为 R ( A , B , x ′ ) R(A,B,x′) R(A,B,x′):
R ( A , B , x ′ ) = x ′ H B − 1 / 2 A B − 1 / 2 x ′ x ′ H x ′ R(A,B,x′)=\frac{x′^HB^{−1/2}AB^{−1/2}x′}{x′^Hx′} R(A,B,x′)=x′Hx′x′HB−1/2AB−1/2x′
利用前面的瑞利商的性质,我们可以很快的知道, R ( A , B , x ′ ) R(A,B,x′) R(A,B,x′)的最大值为矩阵 B − 1 / 2 A B − 1 / 2 B^{−1/2}AB^{−1/2} B−1/2AB−1/2的最大特征值,或者说矩阵 B − 1 A B^{-1}A B−1A的最大特征值,而最小值为矩阵 B − 1 A B^{-1}A B−1A的最小特征值。这里用到了对矩阵进行标准化。
方法三:直接对w进行求偏导
∂ J ( w ) ∂ w = ∂ ∂ w ( w T S b w w T S w w ) = w T S w w ∂ ( w T S b w ) ∂ w − w T S b w ∂ ( w T S w w ) ∂ w = 0 → ( w T S w w ) 2 S b w − ( w T S b w ) 2 S w w = 0 除以 w T S w w : → ( w T S w w w T S w w ) S b w − ( w T S b w w T S w w ) S w w = 0 → S b w − J S w w = 0 → S w − 1 S b w − J w = 0 → J w = S w − 1 S b w → J w = S w − 1 ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w → J w = S w − 1 ( μ 0 − μ 1 ) ( ( μ 0 − μ 1 ) T w ) ) ⏟ c ∈ R → J w = c S w − 1 ( μ 0 − μ 1 ) → w = c J S w − 1 ( μ 0 − μ 1 ) \frac {\partial J(w)}{\partial w} = \frac {\partial }{\partial w}(\frac{w^TS_bw}{w^TS_ww})=w^TS_ww\frac{\partial (w^TS_bw)}{\partial w} - w^TS_bw\frac{\partial (w^TS_ww)}{\partial w} = 0 \\ →(w^TS_ww)2S_bw - (w^TS_bw)2S_ww=0\\ 除以w^TS_ww:\\ →(\frac{w^TS_ww}{w^TS_ww})S_bw - (\frac{w^TS_bw}{w^TS_ww})S_ww=0\\ →S_bw-JS_ww=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ →S_w^{-1}S_bw-Jw=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ →Jw=S_w^{-1}S_bw\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ →Jw=S_w^{-1}(μ_0-μ_1)(μ_0-μ_1)^Tw\ \ \ \ \ \ \ \ \\ →Jw=S_w^{-1}(μ_0-μ_1)\underbrace{((μ_0-μ_1)^Tw))}_{\text c∈R}\ \\ →Jw=cS_w^{-1}(μ_0-μ_1)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ →w=\frac cJS_w^{-1}(μ_0-μ_1)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ∂w∂J(w)=∂w∂(wTSwwwTSbw)=wTSww∂w∂(wTSbw)−wTSbw∂w∂(wTSww)=0→(wTSww)2Sbw−(wTSbw)2Sww=0除以wTSww:→(wTSwwwTSww)Sbw−(wTSwwwTSbw)Sww=0→Sbw−JSww=0 →Sw−1Sbw−Jw=0 →Jw=Sw−1Sbw →Jw=Sw−1(μ0−μ1)(μ0−μ1)Tw →Jw=Sw−1(μ0−μ1)c∈R ((μ0−μ1)Tw)) →Jw=cSw−1(μ0−μ1) →w=JcSw−1(μ0−μ1)
Fisher’s linear discirminant
多类LDA
优化的目标函数:
J ( w ) = W T S b W W T S w W J(w)=\frac{W^TS_bW}{W^TS_wW}\\ J(w)=WTSwWWTSbW
其中:
S b = ∑ j = 1 k N j ( μ j − μ ) ( μ j − μ ) T , μ 为所有样本的均值向量、 N j 为第 j 类样本的个数 S w = ∑ j = 1 k S w j = ∑ j = 1 k ∑ x ∈ X j ( x − μ j ) ( x − μ j ) T S_b=\sum_{j=1}^kN_j(μ_j-μ)(μ_j-μ)^T,μ为所有样本的均值向量、N_j为第j类样本的个数\\ S_w=\sum_{j=1}^kS_{wj}=\sum_{j=1}^k\sum_{x∈X_j}(x-μ_j)(x-μ_j)^T\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Sb=j=1∑kNj(μj−μ)(μj−μ)T,μ为所有样本的均值向量、Nj为第j类样本的个数Sw=j=1∑kSwj=j=1∑kx∈Xj∑(x−μj)(x−μj)T
有一个问题,就是 W T S b W W^TS_bW WTSbW和 W T S w W W^TS_wW WTSwW都是矩阵,不是标量,无法作为一个标量函数来优化!
常见的一个LDA多累优化目标函数定义为:
a r g m a x ⏟ w J ( W ) = ∏ d i a g ( W T S b W ) ∏ d i a g ( W T S w W → J ( W ) = ∏ i = 1 d ( w i T S b w i ) ∏ i = 1 d ( w i T S w w i ) = ∏ i = 1 d w i T S b w i w i T S w w i \underbrace{arg\ max\ }_{\text w} J(W)=\frac{∏diag(W^TS_bW)}{∏diag(W^TS_wW}\\ →J(W)= \frac{∏_{i=1}^d(w_i^TS_bw_i)}{∏_{i=1}^d(w_i^TS_ww_i)}=∏_{i=1}^d\frac{w_i^TS_bw_i}{w_i^TS_ww_i} w arg max J(W)=∏diag(WTSwW∏diag(WTSbW)→J(W)=∏i=1d(wiTSwwi)∏i=1d(wiTSbwi)=i=1∏dwiTSwwiwiTSbwi
广义瑞利商
最大值是矩阵 S w − 1 S b S^{−1}_wS_b Sw−1Sb的最大特征值,最大的d个值的乘积就是矩阵 S w − 1 S b S^{−1}_wS_b Sw−1Sb的最大的d个特征值的乘积,此时对应的矩阵W为这最大的d个特征值对应的特征向量张成的矩阵。
相关文章:
)
线性判别分析(Linear Discriminant Analysis,LDA)
Linear Discriminant Analysis(LDA) 输入: 原始数据$D((x_1,y_1),(x_2,y_2),...,(x_m,y_m)$ 、 类别标签$Y[y_1,y_2,...,y_n]$、 降维到的维度d输出: 投影矩阵W、投影后的样本$Z$、算法步骤: 1.计算类内散度…...
git的分支及标签使用及情景演示
目录 一. 环境讲述 二.分支 1.1 命令 1.2情景演练 三、标签 3.1 命令 3.2 情景演示 编辑 一. 环境讲述 当软件从开发到正式环境部署的过程中,不同环境的作用如下: 开发环境:用于开发人员进行软件开发、测试和调试。在这个环境中…...
深度解析找不到msvcp120.dll相关问题以及解决方法
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“msvcp120.dll丢失”。这个错误通常会导致某些应用程序无法正常运行,给用户带来很大的困扰。那么,如何解决msvcp120.dll丢失的问题呢?本文将为大家介绍…...
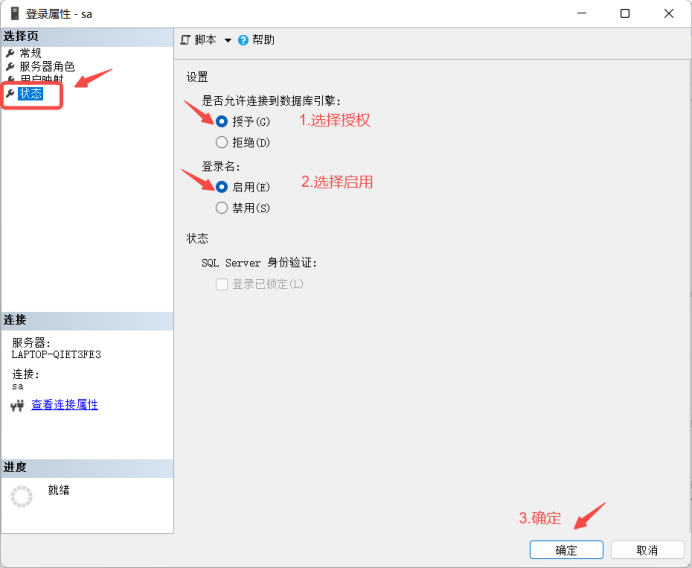
SQL Server 2022 安装步骤——SQL Server设置身份验证教程
目录 前言: 安装详细步骤: 第一步: 第二步: 第三步: 第四步: SQL Server 连接的方式: Window验证: SQL Server验证: 两者之间区别: 总结: SQL Server身份验证登录配置教程: 第一步: 第二步: 第三步: 番外篇: 前言: 本文讲解,如何安装SQL Server安…...

Maven各方面配置好了却无法显示版本
今天配置了maven环境,各方面都配置好了命令行却一直没办法显示maven的版本,原因 竟是两个JDK导致maven无法选择,因为maven依赖于JDK,导致在选择JDK的时候差生了二义 性,在环境变量里面删除不常用的JDK,只…...

Jdk 1.8 for mac 详细安装教程(含版本切换)
Jdk 1.8 for mac 详细安装教程(含版本切换) 官网下载链接 https://www.oracle.com/cn/java/technologies/downloads/#java8-mac 一、选择我们需要安装的jdk版本,这里以jdk8为例,下载 macOS 版本,M芯片下载ARM64版本…...
02MyBatisPlus条件构造器,自定义SQL,Service接口
一、条件构造器 1.MyBatis支持各种复杂的where条件,满足开发的需求 Wrapper是条件构造器,构建复杂的where查询 AbstractWrapper有构造where条件的所有方法,QueryWrapper继承后并有自己的select指定查询字段。UpdateWrapper有指定更新的字段的…...

c语言练习11周(6~10)
输入任意字串,将串中除了首尾字符的其他字符升序排列显示,串中字符个数最多20个。 题干 输入任意字串,将串中除了首尾字符的其他字符升序排列显示,串中字符个数最多20个。输入样例gfedcba输出样例gbcdefa 选择排序 #include<s…...
钉钉API与集简云无代码开发连接:电商平台与营销系统的自动化集成
连接科技与能源:钉钉API与集简云的一次集成尝试 在数字化时代,许多公司面临着如何将传统的工作方式转变为更智能、高效的挑战。某能源科技有限公司也不例外,他们是一家专注于能源科技领域的公司,产品包括节能灯具、光伏逆变器、电…...

C++算法:包含三个字符串的最短字符串
涉及知识点 有序集合 字符串 题目 给你三个字符串 a ,b 和 c , 你的任务是找到长度 最短 的字符串,且这三个字符串都是它的 子字符串 。 如果有多个这样的字符串,请你返回 字典序最小 的一个。 请你返回满足题目要求的字符串。…...

华为开源carbondata中的使用问题处理
carbondata中的使用问题处理 Q:什么是不良记录? A:由于数据类型不兼容而无法加载到CarbonData中的记录或为空或具有不兼容格式的记录被归类为不良记录。 Q:CarbonData中的不良记录存储在哪里? A:不良记录…...

AI:76-基于机器学习的智能城市交通管理
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...

区块链游戏,游戏开发
区块链游戏是一种基于区块链技术的新兴游戏类型,它具有去中心化、安全性高、透明度高、可追溯等特点。与传统的游戏开发相比,区块链游戏开发需要更多的技术和知识储备,同时也需要更加注重游戏本身的玩法和用户体验。 在区块链游戏中ÿ…...

单片机程序无法下载?
原因一:电源问题 电源可能是导致STM32微控制器无法下载程序的一个常见原因。确保电源稳定对于正常运行和下载程序至关重要。以下是一些电源问题: 1. 电源电压不足:如果STM32微控制器没有足够的电压供应,它可能无法正常工作或下载程…...

【数据库】【sql】如何用SQL实现跨行计算
【背景】 这里的跨行计算不是指整体聚合类的函数比如SUM等的功能,而是指递归算法。 比如我接到有需求,有一个结果字段需要是目前所有行该字段的和,这是属于递归类的算法,SQL中如何实现呢? 【方法】 可以使用窗口函数…...
)
Oracle(概念含安装)
Oracle是一种关系数据库管理系统(RDBMS),是由美国甲骨文公司(Oracle Corporation)开发的。它是一个客户端/服务器系统,可以在各种操作系统上运行,包括Windows、Linux和Unix等。Oracle的设计重点…...
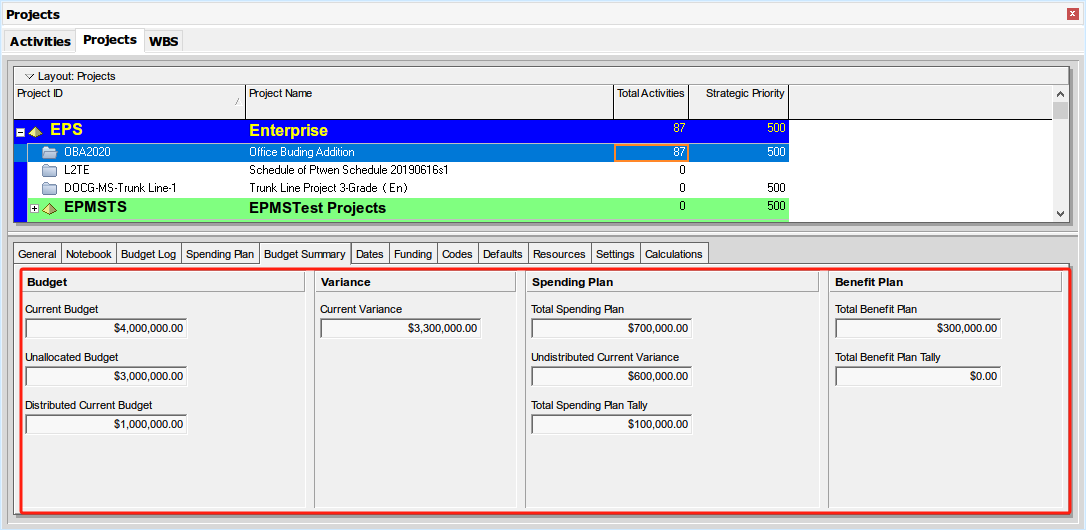
P6入门:项目初始化4-项目详情之预算日志及汇总Budget
前言 使用项目详细信息查看和编辑有关所选项目的详细信息,在项目创建完成后,初始化项目是一项非常重要的工作,涉及需要设置的内容包括项目名,ID,责任人,日历,预算,资金,分类码等等&…...

CSS 中BFC是什么?
在CSS中,BFC(块级格式化上下文)是一个重要的概念,它对于理解和解决布局中的一些问题非常有帮助。本文将深入探讨BFC是什么,以及如何使用代码来详细解释BFC的概念和应用。 引言 在Web开发中,页面布局是一个…...

uniapp的几种跳转方式
1、UniApp是一个跨平台的应用开发框架,可以用于开发同时支持多个平台(如iOS、Android、H5等)的应用程序。在UniApp中,有多种方式可以实现页面之间的跳转。以下是其中一些常用的跳转方式: 页面跳转(navigat…...
【MySQL】初识数据库
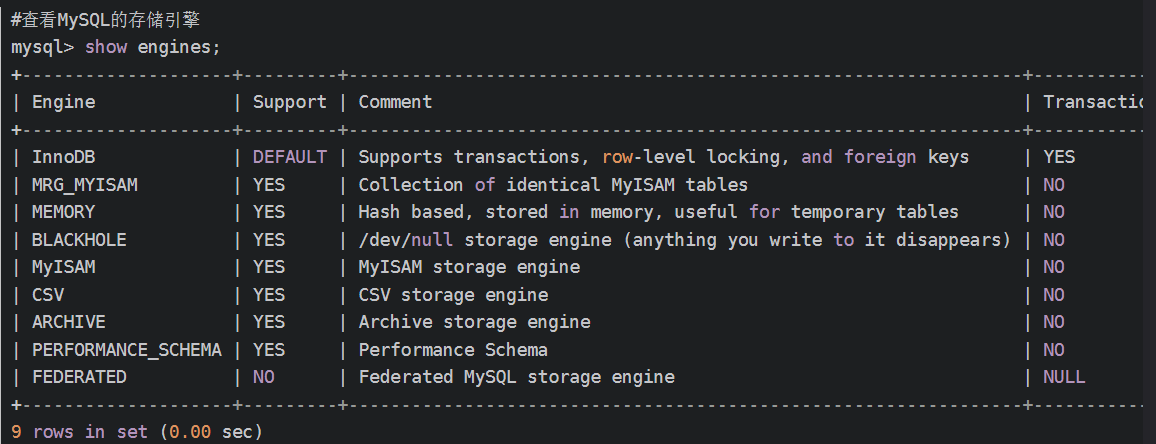
目录 1.概念2.基本使用显示当前的数据库列表创建数据库使用数据库创建表向表中插入数据查看创建的表中的数据 3.SQL的分类4.存储引擎 1.概念 MySQL本质是基于C(mysql)S(mysqld)模式的一种网络服务。 mysqld:它是数据库的服务器端(这是一个守护进程&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
