C++进阶篇4---番外-红黑树
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍,因而是接近平衡的。红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍,因而是接近平衡的。红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的 (即不能出现两个连续的红色结点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径(从根节点到空结点)上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也被叫做NIL)
下图是一个红黑树
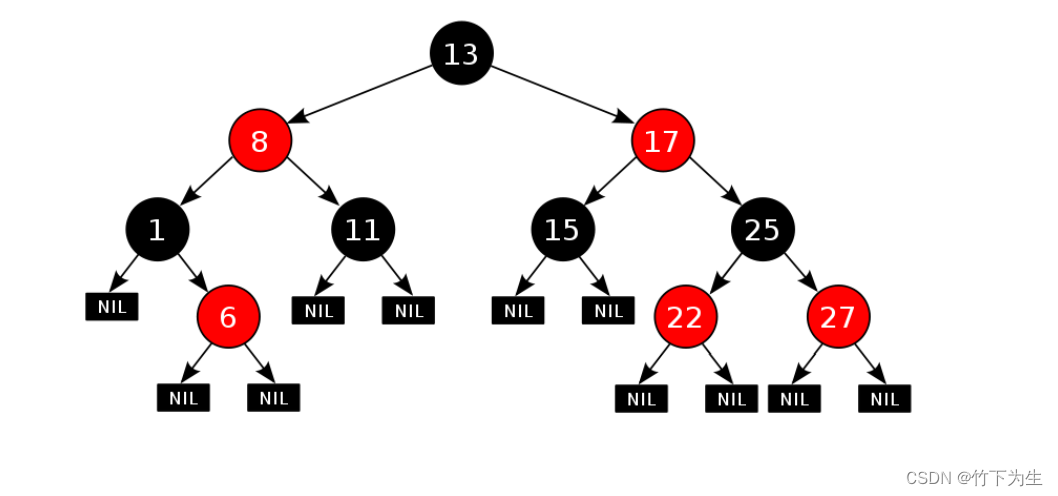
根据红黑树的性质:我们能得到这样一个结论---最长路径不会超过最短路径的两倍,为什么呢?
理由如下:因为每条路径上黑色节点的个数要相同,所以最短的路径上的点均为黑色结点,同时因为不能出现红色结点相邻的情况,所以最长路径上的结点颜色只能是黑红相间,故得出上诉结论
二、红黑树结点定义
enum Colour //这里用的枚举类型,也可以用其他的类型,只要能代表红黑两种颜色就行,如true/false
{BLACK,RED
};template<class K,class V>
struct RBTreeNode {RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;pair<K, V>_kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};思考:为什么要将结点颜色默认设置为红色???
理由如下:由于每条路径上的黑色节点的个数要保持相同,如果我们插入的结点的颜色为黑色,那么必然该节点所在路径的黑色节点的个数要增加,就会导致这颗树的其他所有路径都需要多一个黑色节点,影响范围太大,而如果插入的结点颜色为红色,我们只要关心它所在子树的情况就行,具体看下面的插入操作。故每个新插入结点颜色都默认为红色
三、红黑树插入结点
template <class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool insert(const pair<K,V>&kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//调整红黑树//...}
private:Node* _root = nullptr;
};2.检查新节点插入后,红黑树的性质有没有被破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论 (p-parent g-grandfather u-uncle)
情况一:cur为红,p为红,g为黑,u存在且为红

在这种情况下,我们只要改变结点的颜色就能保持红黑树的性质。
(注意:这种情况下,不用关心cur所在的位置)
情况二:cur为红,p为红,g为黑,u不存在或为黑色

这里就无法通过改变p、g、u的颜色来保持红黑树的性质(读者可以去手玩尝试一下),需要进行旋转+变色才行,那么看到这种形状的图形,我们就应该想到AVL树中的单旋和双旋,上面的情况很明显对应右单旋,旋转之后如下图
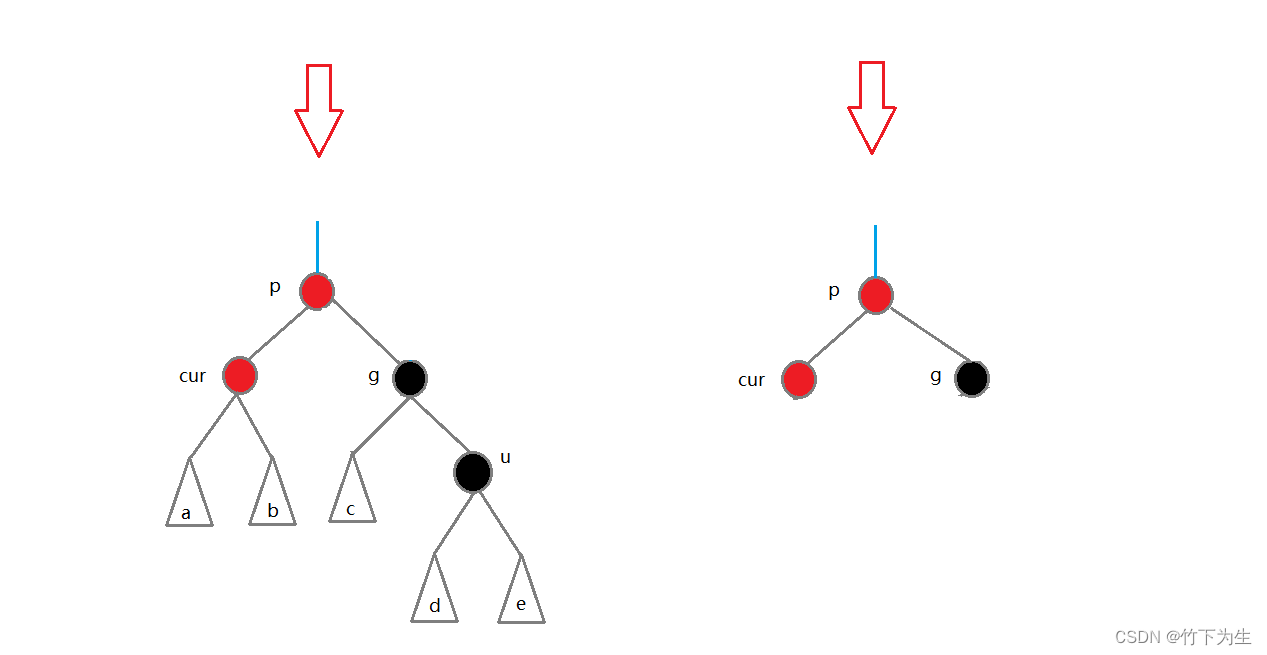
如何改变颜色使得红黑树的性质保持不变?
1.uncle为空,显而易见,将g变为红,p变为黑(可能有人会觉得将cur变成黑不是也行嘛?但如果p为红,且它是子树,那么还需要向上调整,会很麻烦,但如果p为黑色,那么它本身既符合红黑树性质,也并不会对其他的子树产生影响,直接就一步到位了)
2.uncle为黑色,(这种情况下,cur不可能是新插入的结点,只能是情况一向上调整得到的),这里就要分析a,b,c,d,e这几颗子树中黑色节点的个数,显然a,b,c的黑色结点个数相同,d和e的黑色结点比abc少一个,所以将p变为黑色,g变为红色,就能保持红黑树的性质(至于为什么不选择将g变成红色,理由同上)

具体的旋转和AVL树一样,只是红黑树旋转后需要变色,AVL树旋转后需要调整平衡因子,不了解的,可以看我写过的AVL树
这里,我们还要考虑cur所在的位置,共四种情况,第一种情况就是上面所讲的,剩下三种的旋转+变色,留给读者思考【旋转不会的可以去看我之前写的AVL树】
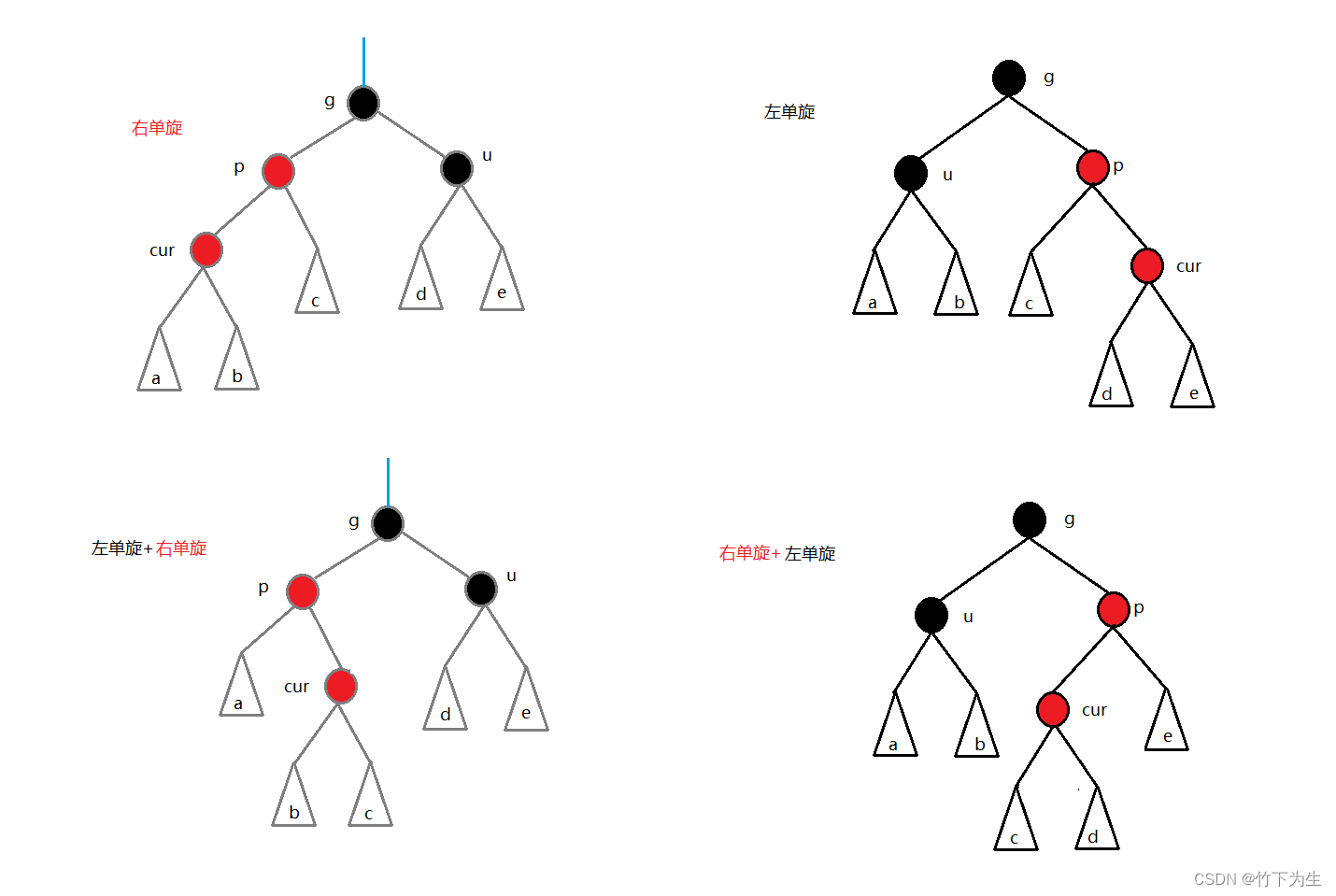
总结:红黑树的结点的插入首先看父节点是否为黑色(插入结点为根的情况要特别判断),如果为黑,不用处理,如果为红,关键看uncle结点,它决定了我们是否需要旋转,如果是红色,则只需要变色,如果是黑色/不存在,我们需要根据cur所在的位置选择合适的旋转方式,并对旋转之后的结点进行变色
代码如下---附带检查检查红黑树是否正确的函数
enum Colour {BLACK,RED
};template<class K,class V>
struct RBTreeNode {RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;pair<K, V>_kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template <class K,class V>
class RBTree {typedef RBTreeNode<K, V> Node;
public:bool insert(const pair<K,V>&kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_parent = parent;if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}//父节点为黑,不用处理//为红需要调整while (parent && parent->_col == RED){// g// p u//cNode* grandparent = parent->_parent;if (grandparent->_left == parent){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED)//情况一{grandparent->_col = RED;parent->_col = uncle->_col = BLACK;cur = grandparent;parent = cur->_parent;}else//情况二{if (parent->_left == cur)//单旋{RotateR(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else//双旋{RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}else{// g// u p// c cNode* uncle = grandparent->_left;if (uncle && uncle->_col == RED){//变色grandparent->_col = RED;parent->_col = uncle->_col = BLACK;//向上走cur = grandparent;parent = cur->_parent;}else{if (parent->_right == cur){RotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* pParent = parent->_parent;subR->_left = parent;parent->_right = subRL;parent->_parent = subR;if (subRL)//注意h==0的情况subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{subR->_parent = pParent;if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* pParent = parent->_parent;subL->_right = parent;parent->_left = subLR;parent->_parent = subL;if (subLR)//注意h==0的情况subLR->_parent = parent;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{subL->_parent = pParent;if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}}}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}bool Isbalance(){return _Isbalance(_root);}//检查是否出现两个连续的红色节点+是否路径上的黑色节点的个数是否相同bool check(Node* root,int blacknum){if (root == nullptr){cout << blacknum << " ";return true;}if (root->_col == RED && root->_parent->_col == RED)return false;if (root->_col == BLACK)blacknum++;return check(root->_left, blacknum) && check(root->_right, blacknum);}bool _Isbalance(Node* root){if (root == nullptr)return true;if (root->_col == RED){cout <<"出现两个连续的红色节点:"<< root->_kv.first << endl;return false;}return check(root->_left, 1) && check(root->_right, 1);}
private:Node* _root = nullptr;
};相关文章:

C++进阶篇4---番外-红黑树
一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路 径会比其他路径长出俩倍࿰…...
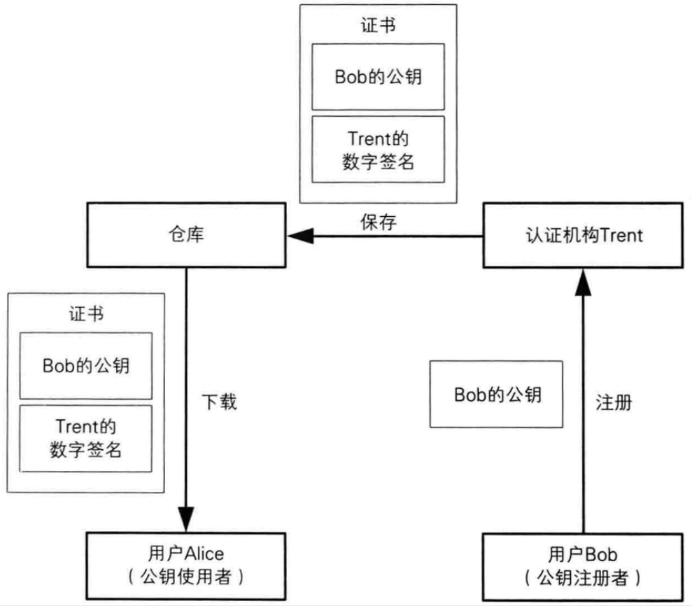
《网络协议》05. 网络通信安全 · 密码技术
title: 《网络协议》05. 网络通信安全 密码技术 date: 2022-09-10 15:16:15 updated: 2023-11-12 07:03:52 categories: 学习记录:网络协议 excerpt: 网络通信安全(ARP 欺骗,DoS & DDoS,SYN 洪水攻击,LAND 攻击&a…...
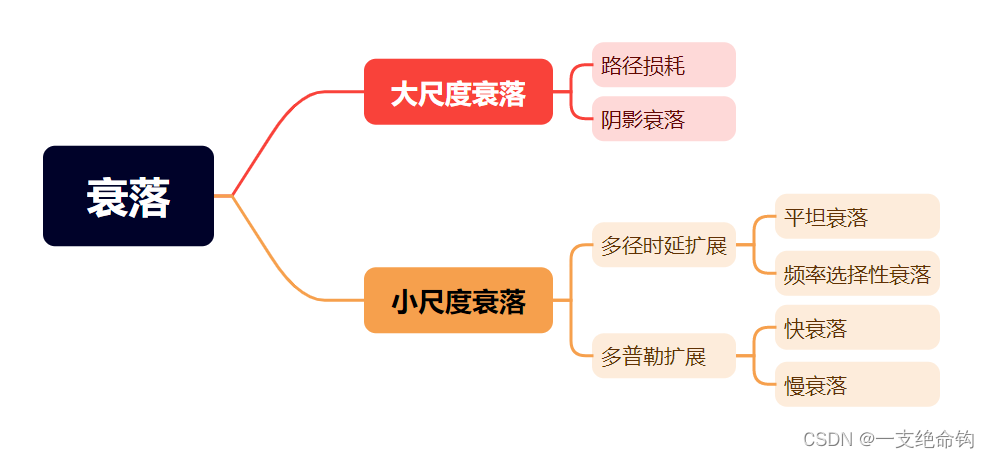
通信信道:无线信道中衰落的类型和分类
通信信道:无线信道中衰落的类型和分类 在进行通信系统仿真时,简单的情况下选择AWGN信道,但是AWGN信道和真是通信中的信道相差甚远,所以需要仿真各种其他类型的信道,为了更清楚理解仿真信道的特点,首先回顾…...

4.HTML网页开发的工具
4. 网页开发的工具 4.1 快捷键 4.1.1 快速复制一行 快捷键:shiftalt下箭头(上箭头) 或者ctrlc 然后 ctrlv 4.1.2 选定多个相同的单词 快捷键: ctrld 4.1.3 添加多个光标 快捷键:ctrlalt上箭头(下箭头&…...
编译报错解决】ASSERT failure in QList<T>::at: “index out of range“)
【Qt5 VS2019 (C++)编译报错解决】ASSERT failure in QList<T>::at: “index out of range“
Qt编译报错提示: ASSERT failure in QList<T>::at: "index out of range", file C:\Qt5\5.15.2\msvc2019_64\include\QtCore/qlist.h, line 571 //load 1st imageQFileInfo fileInfo1 list.at(2);原因: QList的索引越界,超…...

linux环境安装redis,以及常用的操作
1. 下载安装文件 http://download.redis.io/releases/redis-5.0.7.tar.gz 2. 把安装文件上传到 /usr/local/ 目录,并解压缩 tar -zvxf redis-5.0.7.tar.gz 3. 重命名文件夹 mv redis-5.0.7/ redis/ 4. 进入 /usr/local/redis/ 进行编译和安装 make make PREF…...

C++ Qt 学习(六):Qt http 编程
1. http 基础 HTTP 基础教程C Web 框架 drogonoatpp 2. C Qt 用户登录、注册功能实现 login_register.h #pragma once#include <QtWidgets/QDialog> #include "ui_login_register.h" #include <QNetworkReply>class login_register : public QDialog…...
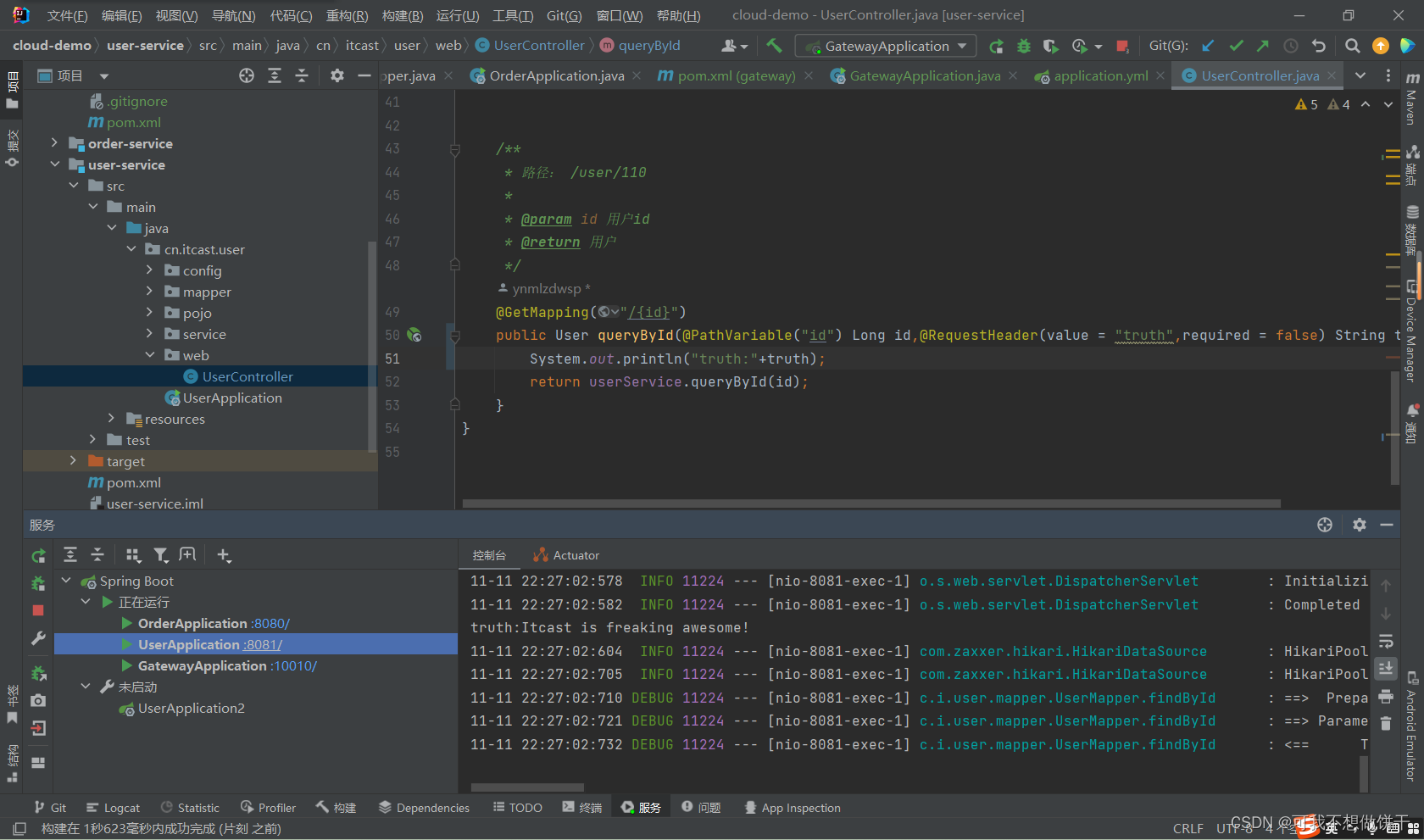
38 路由的过滤器配置
3.3.断言工厂 我们在配置文件中写的断言规则只是字符串,这些字符串会被Predicate Factory读取并处理,转变为路由判断的条件 例如Path/user/**是按照路径匹配,这个规则是由 org.springframework.cloud.gateway.handler.predicate.PathRoute…...

3分钟带你了解前端缓存-HTTP缓存
前情提要 前端缓存分为下面三大类,本文主要讲解HTTP缓存~ 1. HTTP缓存 强缓存协商缓存 2. 浏览器缓存 本地小容量缓存本地大容量缓存 3. 应用程序缓存 HTML5应用程序缓存 缓存作用 减少了冗余的数据传输减少服务器的负担提高了网站的性能加快加载网页速度 …...
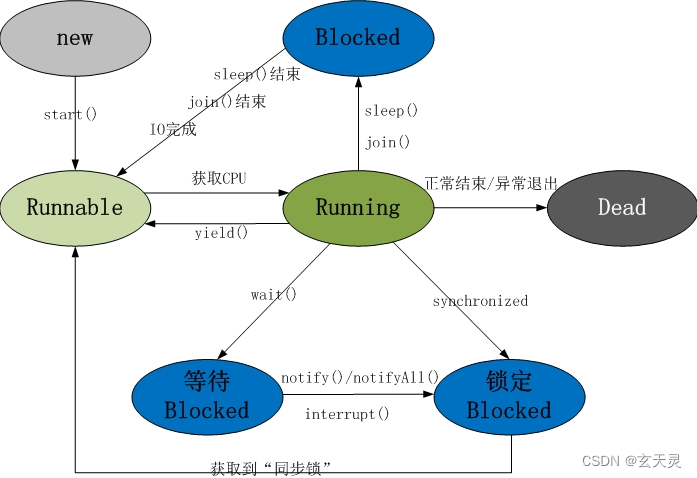
【多线程 - 03、线程的生命周期】
生命周期 当线程被创建并启动以后,它不是一启动就进入执行状态,也不会一直处于执行状态,而是会经历五种状态。 线程状态的五个阶段: 新建状态(New)就绪状态(Runnable)运行状态&…...
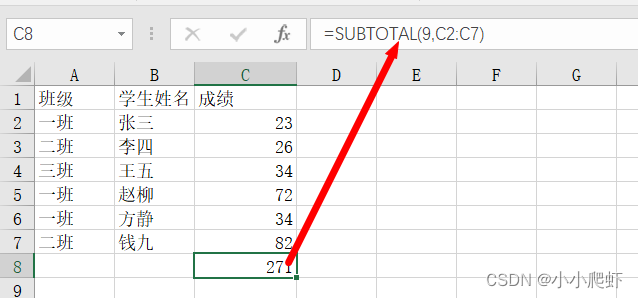
excel表的筛选后自动求和
一般都使用subtotal函数。 通过看一个大佬的视频,发现可以有更简单的方法。 首先任意筛选数据(ctrlshiftl), 然后选中需要求和的列的最下方的空白单元格,再按alt。 回车即可。 实质它还是用的subtotal函数...

2311rust特征
Rust无成本抽象 Rust中抽象基石是trait: 1,Trait是Rust中唯一的接口概念.多个类型可实现一个特征,事实上,可为现有类型提供新的特征实现.另一方面,想抽象未知类型时,找特征就行了. 2,与C模板一样,可静态分发特征. 3,可动态分发特征.有时确实需要间接,所以不必运行时"擦除…...
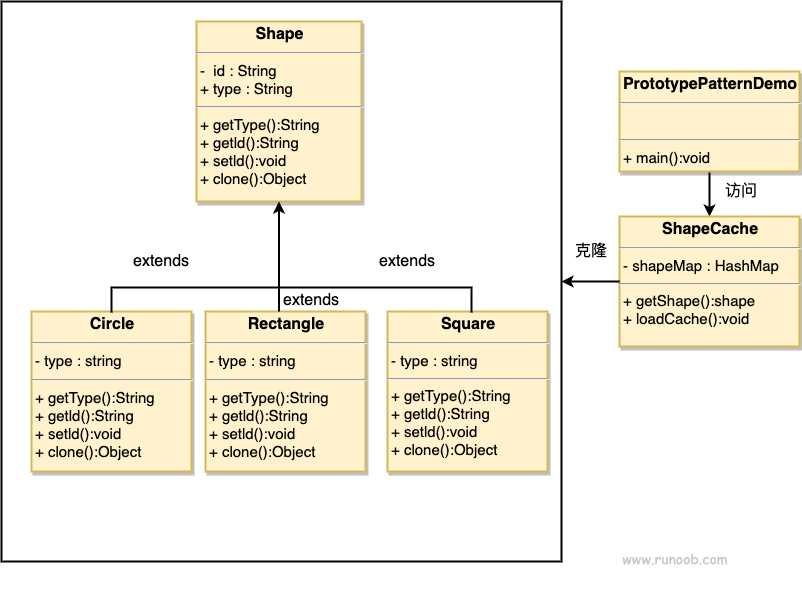
原型模式 rust和java的实现
文章目录 原型模式介绍优点缺点使用场景 实现java 实现rust 实现 rust代码仓库 原型模式 原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当…...
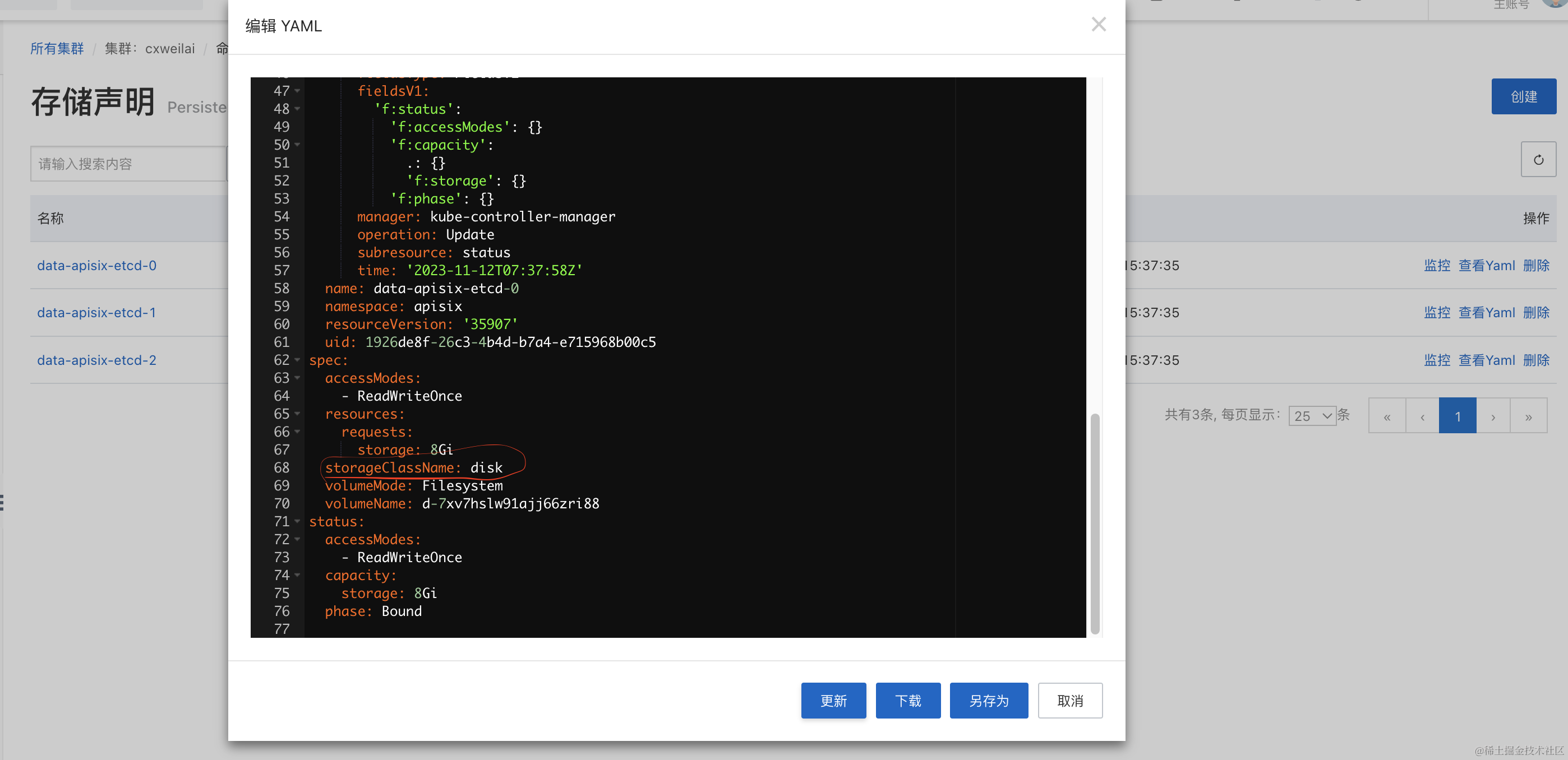
阿里云ACK(Serverless)安装APISIX网关及APISIX Ingress Controller
在k8s上安装apisix全家,通过helm安装很简单,但是会遇到一些问题。 安装 首先登录阿里云控制台,在ACK集群详情页,进入CloudShell,执行下面helm命令安装apisix、apisix-ectd、apisix-dashboard和apisix-ingress-contro…...

vue+mongodb+nodejs实现表单增删改查
ExpressMongodbVue实现增删改查 效果图 前言 最近一直想学下node,毕竟会node的前端更有市场。但是光看不练,感觉还是少了点什么,就去github上看别人写的项目,收获颇丰,于是准备自己照葫芦画瓢写一个。 作为程序员,一…...
SpringBootWeb案例——Tlias智能学习辅助系统(3)——登录校验
前一节已经实现了部门管理、员工管理的基本功能。但并没有登录,就直接访问到了Tlias智能学习辅助系统的后台,这节来实现登录认证。 目录 登录功能登录校验(重点)会话技术会话跟踪方案一 Cookie(客户端会话跟踪技术)会话跟踪方案二…...

hive和spark-sql中 日期和时间相关函数 测试对比
测试版本: hive 2.3.4 spark 3.1.1 hadoop 2.7.7 1、增加月份 add_months(timestamp date, int months)add_months(timestamp date, bigint months)Return type: timestampusage:add_months(now(),1) 2、增加日期 adddate(timestamp startdate, int days)…...

Cell和RefCell
Cell和RefCell CellRefCellRefCell在运行时记录借用结合Rc和RefCell来拥有多个可变数据所有者引用循环与内存泄漏制造引用循环避免引用循环:将Rc变为Weak创建树形数据结构:带子节点的Node增加从子到父的引用可视化strong_count 和 weak_count 的改变 Rus…...
开发笔记 20231113)
DaoWiki(基于Django)开发笔记 20231113
DaoWiki(基于Django)开发笔记 20231113 开发环境 操作系统 windows11python版本 3.12.0django版本 4.2.7 构建python虚拟环境 python -m venv daowiki启动python虚拟环境 cd daowiki\Scripts .\activate安装Django pip install django4.2.7创建项目…...
照片放大软件 Topaz Gigapixel AI mac中文版简介
Topaz Gigapixel AI mac是一款使用人工智能功能扩展图像的桌面应用程序,同时添加自然细节以获得惊人的效果。使用深度学习技术,A.I.Gigapixel™可以放大图像并填写其他调整大小的产品遗漏的细节,使用A.I.Gigapixel™,您可以裁剪照…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
