CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。

CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。
概述
时空函数是一种用于描述时空结构和演化的函数。它在物理学、数学和计算机科学等领域中都有广泛的应用。时空函数可以描述物体在时空中的位置、速度、加速度以及其他相关属性。
用法
CnosDB 将使用一种全新的数据类型 Geometry来支持地理信息系统。
创建表的时候可以指定列的类型为Geometry:
create table geo_table (geo geometry(<object_type>, )
);
目前 CnosDB 中使用 WKT 格式来存储Geometry类型,Geometry类型下有 7 种几何对象:
WKT 是是一种开放的国际标准,全拼为 Well-Known Text 。
| 几何对象 | 语法描述 |
| 点 | POINT(<x1><y1>) |
| 线 | LINESTRING(<x1><y1>,<x2><y2>,...) |
| 多边形 | POLYGON((<x1><y1>,<y1><y2>)) |
| 多点 | MULTIPOINT (<x1> <y1>, <x2> <y2>, ...) |
| 多线 | MULTILINESTRING ((<x1> <y1>, <x2> <y2>, ...), (<x1> <y1>, <x2> <y2>, ...)) |
| 多面(多多边形) | MULTIPOLYGON (((<x1> <y1>, <x2> <y2>, ...)), ((<x1> <y1>, <x2> <y2>, ...))) |
| 几何对象集合 | GEOMETRYCOLLECTION (<geometry tag1> <wkt data1>, <geometry tag2> <wkt data2>, ...) |
示例
| 几何对象 | 示例 |
| 点 | POINT(30 10) |
| 线 | LINESTRING (30 10, 10 30, 40 40) |
| 多边形 | POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10)) |
| POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10), (20 30, 35 35, 30 20, 20 30)) | |
| 多点 | MULTIPOINT ((10 40), (40 30), (20 20), (30 10)) |
| MULTIPOINT (10 40, 40 30, 20 20, 30 10) | |
| 多线 | MULTILINESTRING ((10 10, 20 20, 10 40), (40 40, 30 30, 40 20, 30 10)) |
| 几何对象集合 | GEOMETRYCOLLECTION (POINT (40 10), LINESTRING (10 10, 20 20, 10 40), POLYGON ((40 40, 20 45, 45 30, 40 40))) |
支持函数
为了更好地操纵 Geometry 类型,CnosDB 提供了 ST_Geometry SQL 系列的函数,来计算几何体的性质和几何体之间的关系
ST_AsBinary(geometry)
将几何对象转换为 WKB 格式,WKB 格式是由 OpenGIS 规范定义的,用于以二进制流的形式交换几何数据,二进制流由含几何 WKB 信息的 BLOB 值表示。
参数类型:Geometry
返回类型:Binary
示例:
select ST_AsBinary('POINT (1 1)')返回结果为16进制:
+--------------------------------------------+
| st_AsBinary(Utf8("POINT (1 1)")) |
+--------------------------------------------+
| 0101000000000000000000f03f000000000000f03f |
+--------------------------------------------+第一个字节表示数据的字节序:01
后面4个字节表示对象的几何类型 :01000000
POINT的值X和Y用8字节double类型的数据表示:000000000000F03F,000000000000F03F
ST_GeomFromWKB
功能:把WKB格式二进制转为Geometry类型
参数类型: Binary
返回类型: Geometry
示例:
SELECT ST_GeomFromWKB(ST_AsBinary('POINT(0 3)'))返回的结果:
+-------------------------------------------------+
| st_GeomFromWKB(st_AsBinary(Utf8("POINT(0 3)"))) |
+-------------------------------------------------+
| POINT(0 3) |
+-------------------------------------------------+ST_Distance(geometry1, geometry2)
功能: ST_Distance 返回两个几何体的 2D 投影之间的最小欧氏距离。
参数类型:Binary
返回类型: Double
示例:
两点间距离
SELECT ST_Distance('POINT(1 0)', 'POINT(0 0)',);+----------------------------------------------------+
| st_distance(Utf8("POINT(1 0)"),Utf8("POINT(0 0)")) |
+----------------------------------------------------+
| 1.0 |
+----------------------------------------------------+返回结果:
+----------------------------------------------------+
| st_distance(Utf8("POINT(1 0)"),Utf8("POINT(0 0)")) |
+----------------------------------------------------+
| 1.0 |
+----------------------------------------------------+点到直线距离
SELECT ST_Distance('POINT(0 0)', 'LINESTRING (30 10, 10 30, 40 40)');返回结果:
+--------------------------------------------------------------------------+
| st_distance(Utf8("POINT(0 0)"),Utf8("LINESTRING (30 10, 10 30, 40 40)")) |
+--------------------------------------------------------------------------+
| 28.284271247461902 |
+--------------------------------------------------------------------------+平面和平面之间的距离
SELECT ST_Distance('POLYGON((0 2,1 1,0 -1,0 2))', 'POLYGON((-1 -3,-2 -1,0 -3,-1 -3))') as distance;返回结果
+--------------------+
| distance |
+--------------------+
| 1.4142135623730951 |
+--------------------+ST_Area(geometry)
功能:返回几何对象 2D 投影的笛卡尔面积。面积单位与用于表示输入几何体坐标的单位相同。 对于点、线串、多点和多线串,此函数返回 0。 对于几何体集合,它返回集合中几何体的面积之和。
参数类型: Geometry
返回类型: Double
示例:
SELECT ST_Area('POLYGON ((40 40, 20 45, 45 30, 40 40))') as area;+------+
| area |
+------+
| 87.5 |
+------+返回结果
+------+
| area |
+------+
| 87.5 |
+------+
注意:部分几何图形不支持计算面积,对这些几何体计算面积会返回 0,如:Point、MultiPoint、LineString、MultiLineString、Line。 如果参数内容格式非法,返回值为 NULL。
案例:物联网场景监控车辆驶入电子围栏
下面有一张表 car。
表car记录车辆的实时位置, id 唯一指示一辆车, location 是车的实时坐标。
create table car (location: geometry(point, 0),tags(id)
);这里有一种圆形的电子围栏,坐标为117.20, 39.12, 半径为0.0008。
1.计算此时电子围栏中的车辆数量
select count(*)
from(select max(time), id, location from car group by id, location
)
where st_distance(location, 'POINT (117.20, 39.12)') < 0.0008; 首先通过max 聚合时间列,找到每辆车最新的位置记录,
然后使用 空间函数 st_distance 找到离电子围栏距离小于电子围栏半径的车辆 ,最后使用 count计算数量。
2.计算车 A5678 的最先进入电子围栏的时间以及最后在电子围栏内的时间。
select min(time), max(time)
from car
where id = 'A5678' and st_distance(location, 'POINT (117.20, 39.12') < 0.0008;
通过 id 筛选出指定车的记录,再使用 空间函数st_distance过滤出该车坐标在电子围栏中的记录,最后使用 min max 聚合函数找出时间。
以上就是 CnosDB2.4 关于时空函数的功能,你可以利用这些功能来处理和分析时空数据,使用时空函数可以帮助你解决许多与地理位置相关的问题,无论是在物流规划、位置分析、地理信息系统还是其他领域,都可以从时空数据中提取有价值的信息,帮助您做出更明智的决策,优化业务流程,并提供更好的服务。
无论您是专业的地理信息系统专家,还是对地理位置数据感兴趣的普通用户,时空函数都将为您提供强大而有用的查询和分析工具。让我们一起利用时空函数,挖掘地理数据的无限潜力!欢迎加入这个精彩的时空分析的世界!
CnosDB简介
CnosDB是一款高性能、高易用性的开源分布式时序数据库,现已正式发布及全部开源。
欢迎关注我们的社区网站:https://cn.cnosdb.com
相关文章:

CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。
CnosDB 在最近新发布的 2.4.0 版本中增加对时空函数的支持。 概述 时空函数是一种用于描述时空结构和演化的函数。它在物理学、数学和计算机科学等领域中都有广泛的应用。时空函数可以描述物体在时空中的位置、速度、加速度以及其他相关属性。 用法 CnosDB 将使用一种全新的…...

python实现炒股自动化,个人账户无门槛量化交易的开始
本篇作为系列教程的引子,对股票量化程序化自动交易感兴趣的朋友可以关注我,现在只是个粗略计划,后续会根据需要重新调整,并陆续添加内容。 股票量化程序化自动交易接口 很多人在找股票个人账户实现程序化自动交易的接口࿰…...

推荐系统笔记--Swing模型的原理
1--Swing模型的引入 在 Item CF 召回中,物品的相似度是基于其受众的交集来衡量的,但当受众的交集局限在一个小圈子时,就会误将两个不相似的物品定义为相似; Swing 模型引入用户的重合度来判断两个用户是否属于一个小圈子ÿ…...
联想小新Pro14默认设置的问题
联想小新Pro14 锐龙版,Win11真的挺多不习惯的,默认配置都不符合一般使用习惯。 1、默认人走过自动开机。人机互动太强了; 2、默认短超时息屏但不锁屏,这体验很容易觉得卡机然后唤起,却又不用密码打开; 3…...
)
【洛谷 P5019】[NOIP2018 提高组] 铺设道路 题解(分治算法+双指针)
[NOIP2018 提高组] 铺设道路 题目背景 NOIP2018 提高组 D1T1 题目描述 春春是一名道路工程师,负责铺设一条长度为 n n n 的道路。 铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n n n 块首尾相连的区域,一开始,第 i i i …...

牛客刷题记录11.12
继承和组合 二进制数统计 1的个数 和 0 的个数...
NextJS开发:使用IconPark、Lucide图标库
IconPark、Lucide两个很不错的图标库,如果需要用到微信、阿里等国内logo可以使用IconPark,Lucide中没有包含这些内容。 安装IconPark npm install icon-park/react --save简单使用 import {Home} from icon-park/react;<Home/> <Home theme&…...
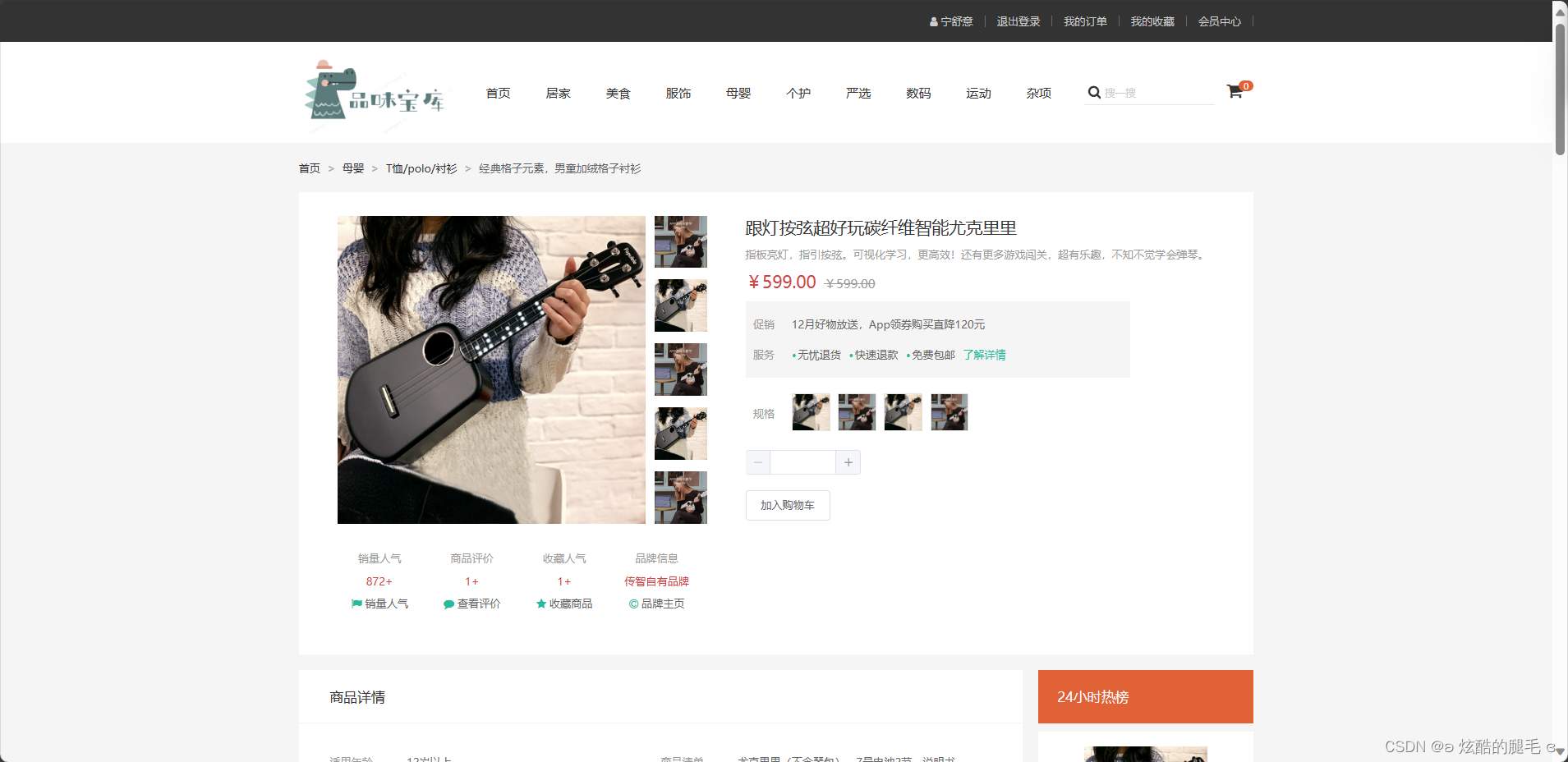
11.12总结
这一周主要写了个人中心的几个功能,资料修改,收货地址的创建和修改删除,还有主页界面和商品界面...

Gogs安装和部署教程-centos上
0、什么是 Gogs? Gogs 是一款极易搭建的自助 Git 服务。 Gogs 的目标是打造一个最简单、最快速和最轻松的方式搭建自助 Git 服务。使用 Go 语言开发使得 Gogs 能够通过独立的二进制分发,并且支持 Go 语言支持的 所有平台,包括 Linux、Mac OS X、Windo…...

Unity中Shader雾效的实现方法一
文章目录 前言一、在片元着色器中使用如下公式计算最终的颜色 lerp(雾效颜色,物体颜色,雾效混合因子)1、获取雾效颜色2、物体的颜色一般通过纹理采样得到,此处用 1 代替测试3、获取 雾效混合因子(由 雾的距离 和 雾的浓度决定&am…...
Mac安装配置Tomcat,以及使用(详解)
目录 一、Tomcat下载: 1、左栏选择Tomcat版本 2、点击下载即可,任选其一 编辑3、下载好的文件夹放到用户名下即可(之前已经下载过,这里以Tomcat 8.5.88为演示),这里提供8.5.88的安装包: 二…...
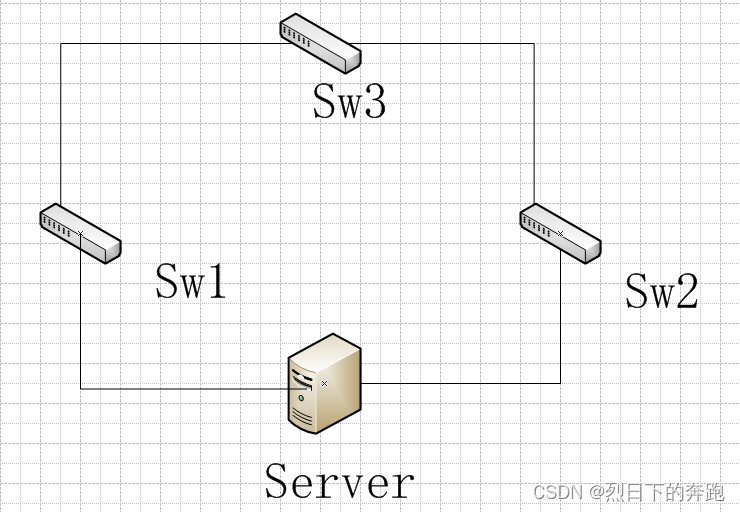
Smart Link 和 Monitor Link应用
定义 Smart Link常用于双上行链路组网,提高接入的可靠性。 Monitor Link通过监视上行接口,使下行接口同步上行接口状态,起到传递故障信息的作用。 Smart Link,又叫做备份链路。一个Smart Link由两个接口组成,其中一个…...
【debug】解决Kali虚拟机开机黑屏,左上角光标一直闪动无法开机问题
做网络攻防实验时,突然Kali无法打开,遇到这个问题。。。。。。 遇到的问题 突然kali虚拟机变成如下黑屏,无法开机,左上角光标闪动,重启无效。 解决办法 在上图界面,按Ctrl F3(不同电脑快捷键…...
)
目标检测YOLO实战应用案例100讲-基于改进YOLO算法的道路交通目标检测(续)
目录 3.3 实验结果与分析 3.3.1 实验数据集 3.3.2 算法的评价指标 3.3.3 损失函数实验结果...

爬虫怎么伪装才更安全
随着网络技术的不断发展,爬虫技术也越来越成熟,爬虫伪装技术也随之得到了广泛应用。在爬虫伪装技术中,如何伪装成正常的浏览器行为,让目标网站无法辨别出爬虫的存在,是爬虫伪装技术的核心。下面,我将从以下…...
)
openssl+sha256开发实例(C++)
文章目录 一、 sha256介绍二、sha256原理三、openssl sha256实现 一、 sha256介绍 SHA-256(Secure Hash Algorithm 256-bit)是一种哈希算法,属于 SHA-2(Secure Hash Algorithm 2)家族的一员。SHA-256 产生的哈希值是一…...

【Bug】当用opencv库的imread()函数读取图像,用matplotlib库的plt.imshow()函数显示图像时,图像色彩出现偏差问题的解决方法
一,问题描述 我们在利用opencv的imread读取本地图像,进行一系列处理,但是发现用matplotlib库的imshow()函数显示的时候出现色彩改变,比如图像偏黄,偏红,偏蓝等等,但是对…...

通过顶顶通呼叫中心中间件玩转FreeSWITCH媒体流
怎么获取FreeSWITCH的媒体流是一个老生常谈的问题了,最常见的方法media_bug,我在2019年就做的FreeSWITCH对接ASR开源的例子https://gitcode.net/iyaosan/FreeSWITCH-ASR用的就是media_bug,对接ASR常见的方法还有通过mod_mrcp模块对接mrcp的asrserver。 …...
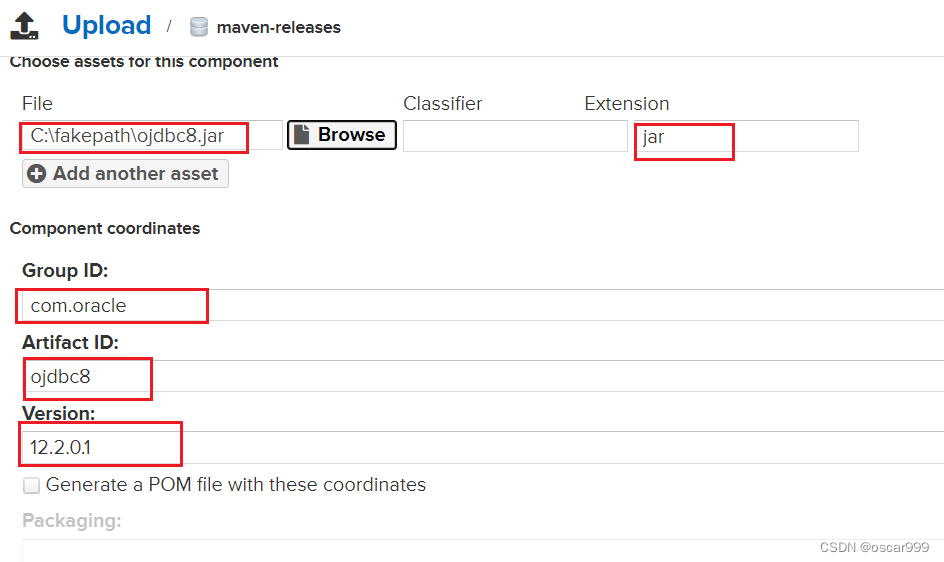
Maven内网开发使用离线仓库
Maven内网开发使用离线仓库 离线或者内网环境开发与外网不通,中央仓库连不上,使用 Maven 管理项目会遇到很多问题。 比如:依赖包缺失,内网的Nexus私服的包老旧,很久没有维护,项目无法运行打包,…...

CSS特效007:绘制3D文字,类似PS效果
css实战中,怎么绘制3D文字呢? 实际上理论很简单,使用text-shadow,根据需要调整阴影的颜色、大小、偏移量等参数,以达到你想要的立体效果。下面是一个简单的示例。关键点就是知道如何设置text-shadow。 效果图 源代码 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
