python线性回归实现
import random
import torch# ①根据带有噪声的线性模型构造一个人造数据集。 使用线性模型参数w=[2,−3.4] b=4.2和噪声项ϵ生成数据集及其标签
def synthetic_data(w, b, num_examples):"""生成 y = Xw + b + 噪声。"""# 生成均值为0,标准差为1,行为num_examples = 1000,列为len(w)=2的矩阵,也就是从一个标准正态分布N~(0,1),提取一个1000*2的矩阵。X = torch.normal(0, 1, (num_examples, len(w)))# 此时X为1000*2的矩阵,也就是二维张量,w为向量,也就是一维张量,符合normal运算的第四种情况,此时将w转置为列向量,也就是2*1的矩阵,做矩阵乘法结果为1000*1的列向量。y = torch.matmul(X, w)+b# 生成均值为0,标准差为0.01的噪声加上y,返回新的yy += torch.normal(0, 0.01, y.shape)# 返回X 将y转置成1列后返回return X, y.reshape((-1, 1))
# 定义w
true_w = torch.tensor([2, -3.4])
# 定义b
true_b = 4.2
# 生成数据集和标签
features, labels = synthetic_data(true_w, true_b, 1000)
# 打印第一个特征和标签,观察数据集和特征格式
print('features:', features[0], '\nlabel:', labels[0])# ②定义一个data_iter 函数, 该函数接收批量大小、特征矩阵和标签向量作为输入,生成大小为batch_size的小批量
def data_iter(batch_size, features, labels):# features的len应该是1000num_examples = len(features)# rang(1000)的一个数据再list一下组成一个列表indices = list(range(num_examples))# 把序列进行一下乱序random.shuffle(indices)# 返回一个数据集和标签for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]
# 定义尺寸
batch_size = 10
# 打印
for X, y in data_iter(batch_size, features, labels):print(X, '\n', y)break# ③定义 初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)# ④定义模型
def linreg(X, w, b):"""线性回归模型。"""return torch.matmul(X, w) + b# ⑤定义损失函数
def squared_loss(y_hat, y):"""均方损失。"""return (y_hat - y.reshape(y_hat.shape))**2 / 2# ⑥定义优化算法
def sgd(params, lr, batch_size):"""小批量随机梯度下降。"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()# ⑦训练过程
# 定义学习率(理解为梯度下降中的步长不知道对不对)
lr = 0.03
# 定义学习几轮
num_epochs = 5
# 定义网络
net = linreg
# 定义损失函数
loss = squared_lossfor epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y)l.sum().backward()sgd([w, b], lr, batch_size)with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')print(f'b的估计误差: {true_b - b}')
学习第三轮时候基本已经稳定
epoch 1, loss 0.035958
w的估计误差: tensor([ 0.0963, -0.1706])
b的估计误差: tensor([0.1828])
epoch 2, loss 0.000128
w的估计误差: tensor([ 0.0048, -0.0085])
b的估计误差: tensor([0.0081])
epoch 3, loss 0.000050
w的估计误差: tensor([ 0.0003, -0.0001])
b的估计误差: tensor([0.0006])
epoch 4, loss 0.000050
w的估计误差: tensor([4.5466e-04, 1.8120e-05])
b的估计误差: tensor([0.0004])
epoch 5, loss 0.000050
w的估计误差: tensor([3.6359e-05, 3.4094e-05])
b的估计误差: tensor([0.0004])Process finished with exit code 0
相关文章:

python线性回归实现
import random import torch# ①根据带有噪声的线性模型构造一个人造数据集。 使用线性模型参数w[2,−3.4] b4.2和噪声项ϵ生成数据集及其标签 def synthetic_data(w, b, num_examples):"""生成 y Xw b 噪声。"""# 生成均值为0,标…...
【JavaEESpring】认识Spring
认识Spring 1. 什么是框架2. SpringBoot 介绍2.1 Spring 的介绍2.2 SpringBoot 1. 什么是框架 框架(Framework) ,意思是框架、机制、准则。通俗的来讲: 框架是实现某种功能的半成品, 他提供了⼀些常⽤的⼯具类, 我们在框架的基础上, 可以更加⾼效的进⾏开发 后端框…...
)
Rust逆向学习 (5)
文章目录 Reverse for Vecvec! 与 添加元素元素访问元素遍历枚举数组弹出最后一个元素——pop 总结 本文将对Rust中的通用集合类型——动态数组 Vec进行学习,对应参考书中的第8章。 Reverse for Vec Vec是Rust中的动态数据结构,与C中的vector功能类似。…...
)
89.STL-函数对象的使用(仿函数)
目录 1.什么是函数对象 2.仿函数示例 3.代码示例 1.什么是函数对象 函数对象是C中的一种编程概念,也称为函数符或仿函数。其实就是重载“()”操作符,使得类对象可以像函数那样调用。 分类:假定某个类有一个重载的operator(),而且重载的oper…...
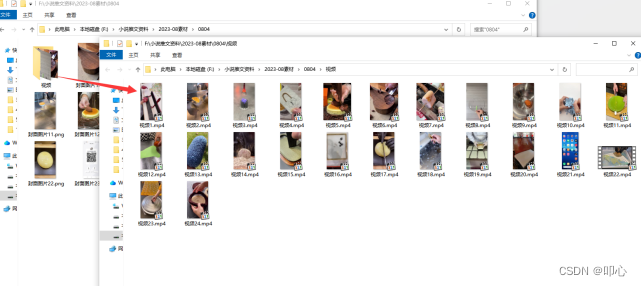
文件管理技巧:按文件容量大小分类,自动移动至目标文件夹的方法
按文件容量大小分类可以帮助快速识别和筛选出不同大小的文件。这样做有很多好处。首先,可以轻松地查找和访问特定大小的文件,提高工作效率。其次,通过将不同大小的文件分类,可以更好地了解和掌控文件的使用情况,避免存…...
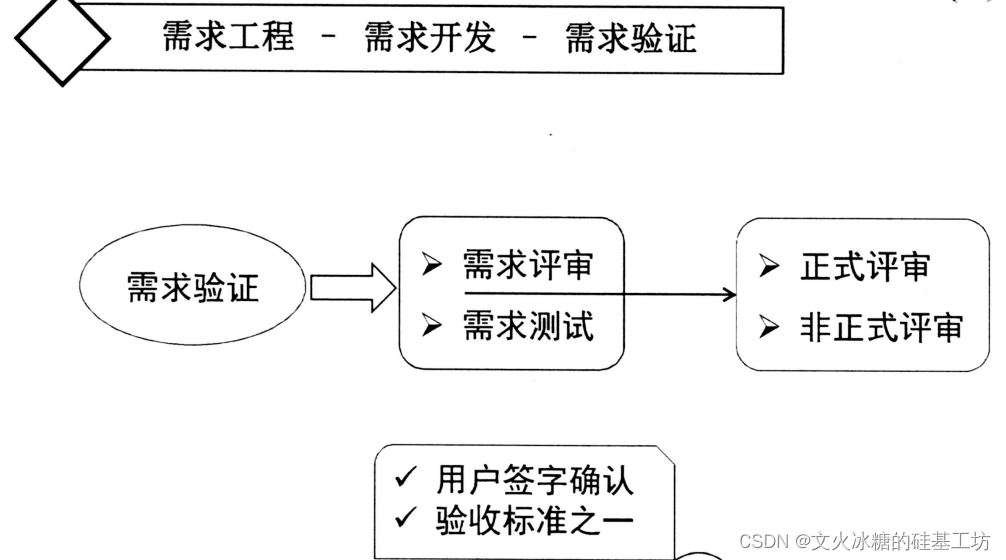
[架构之路-246]:目标系统 - 设计方法 - 软件工程 - 需求工程- 需求开发:获取、分析、定义、验证
目录 前言: 架构师为什么需要了解需求分析 一、需求工程概述 1.1 概述 1.2 需求工程的两大部分 (1)需求开发:系统工程师的职责、目标系统开发角度 (2)需求管理:项目管理者的职责、项目管…...
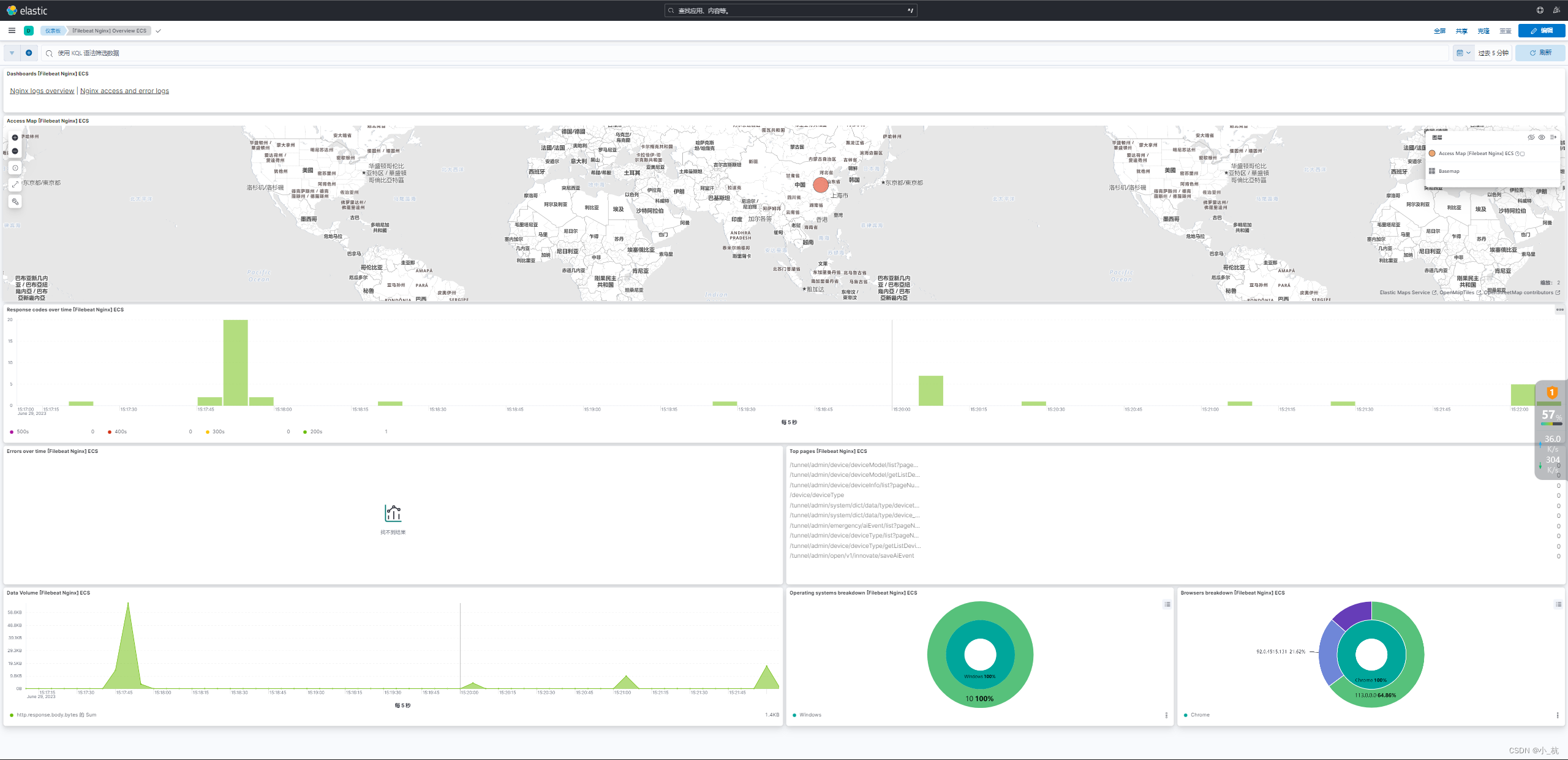
轻量日志管理方案-[EFK]
使用FileBeat进行日志文件的数据收集,并发送到ES进行存储,最后Kibana进行查看展示; 这个应该是最简单,轻量的日志收集方案了。 最总方案为:FileBeatESKibana ; 【Kibana过于强大,感觉可以无限扩展】 文章目…...
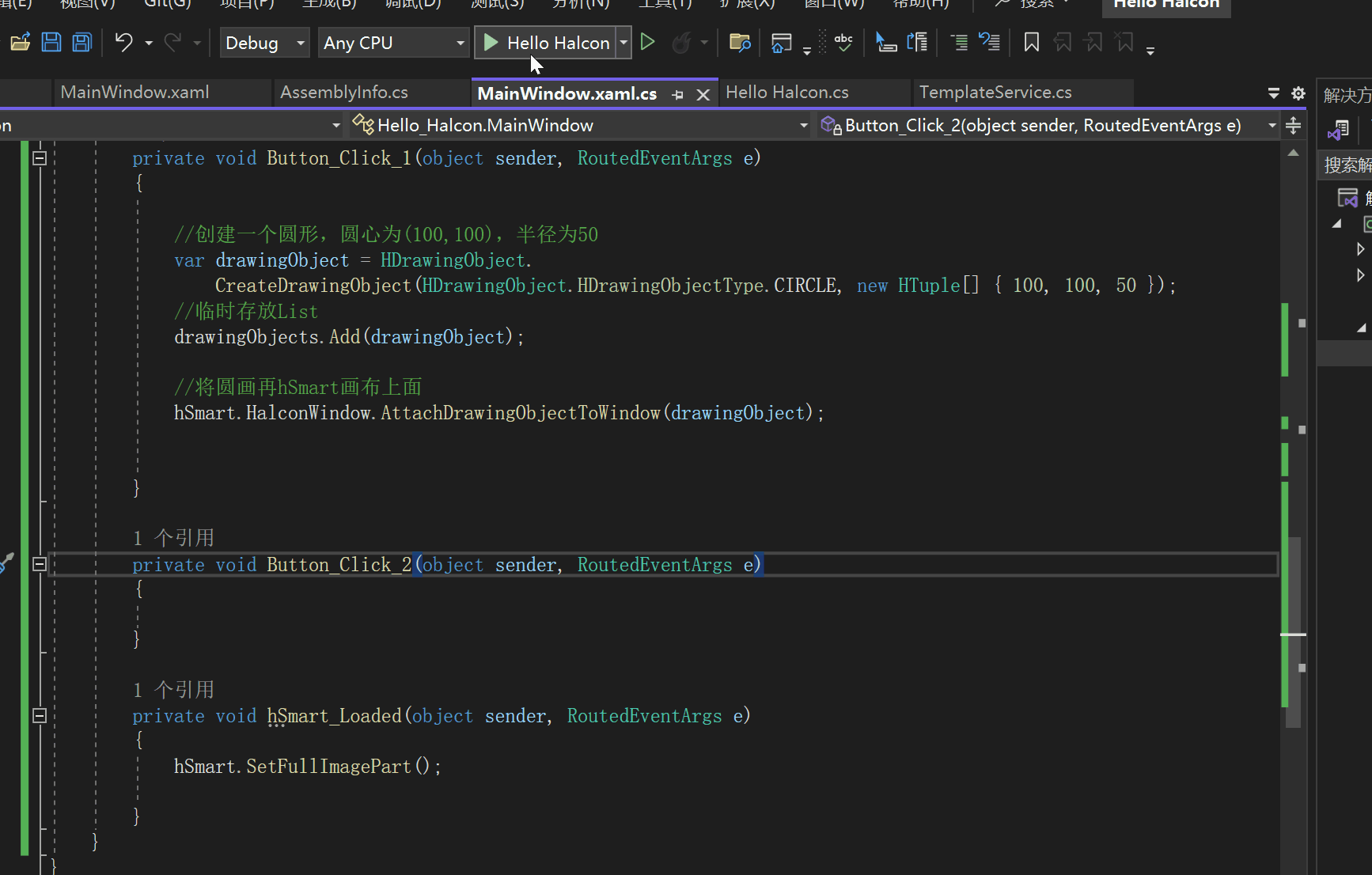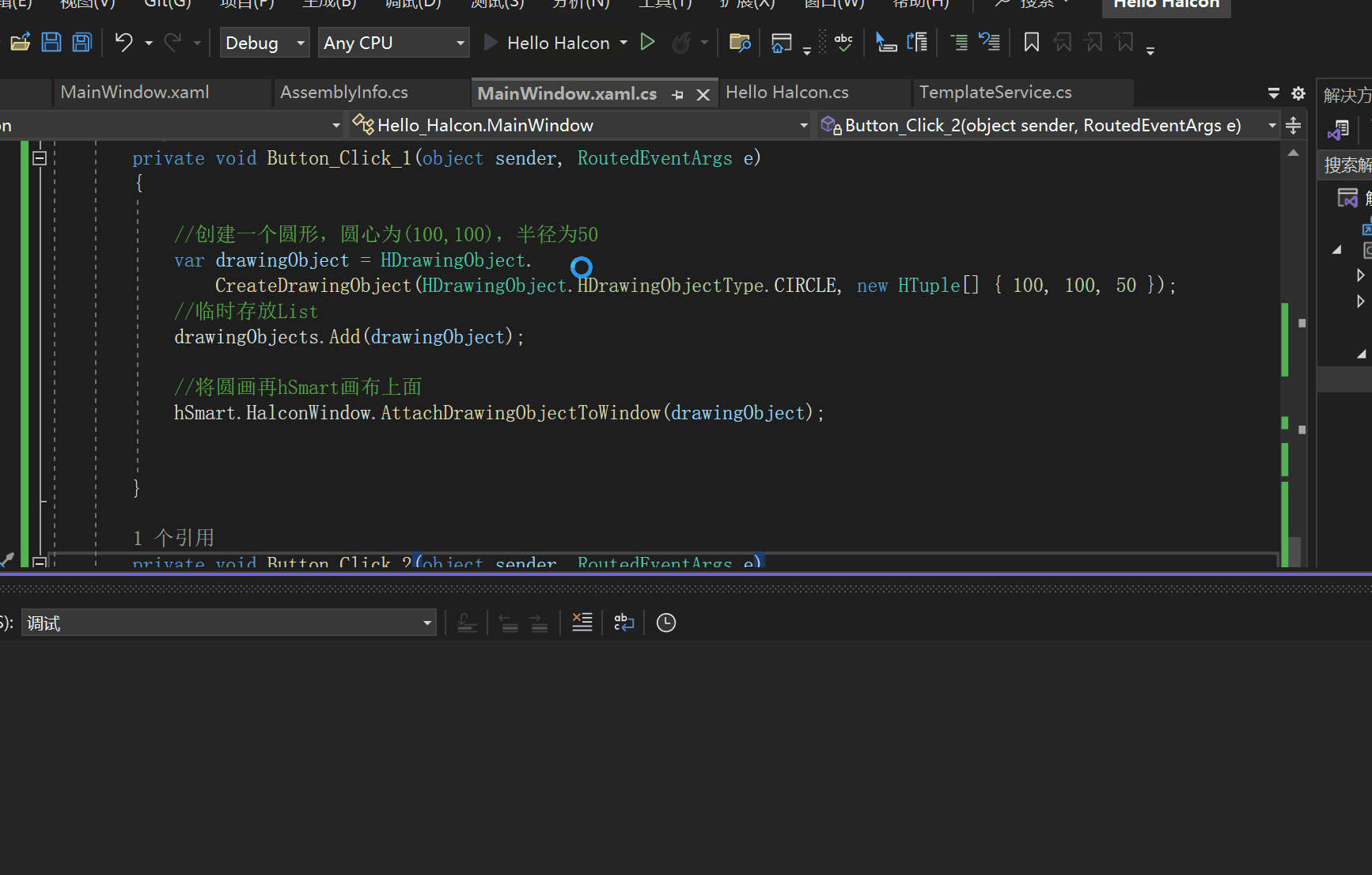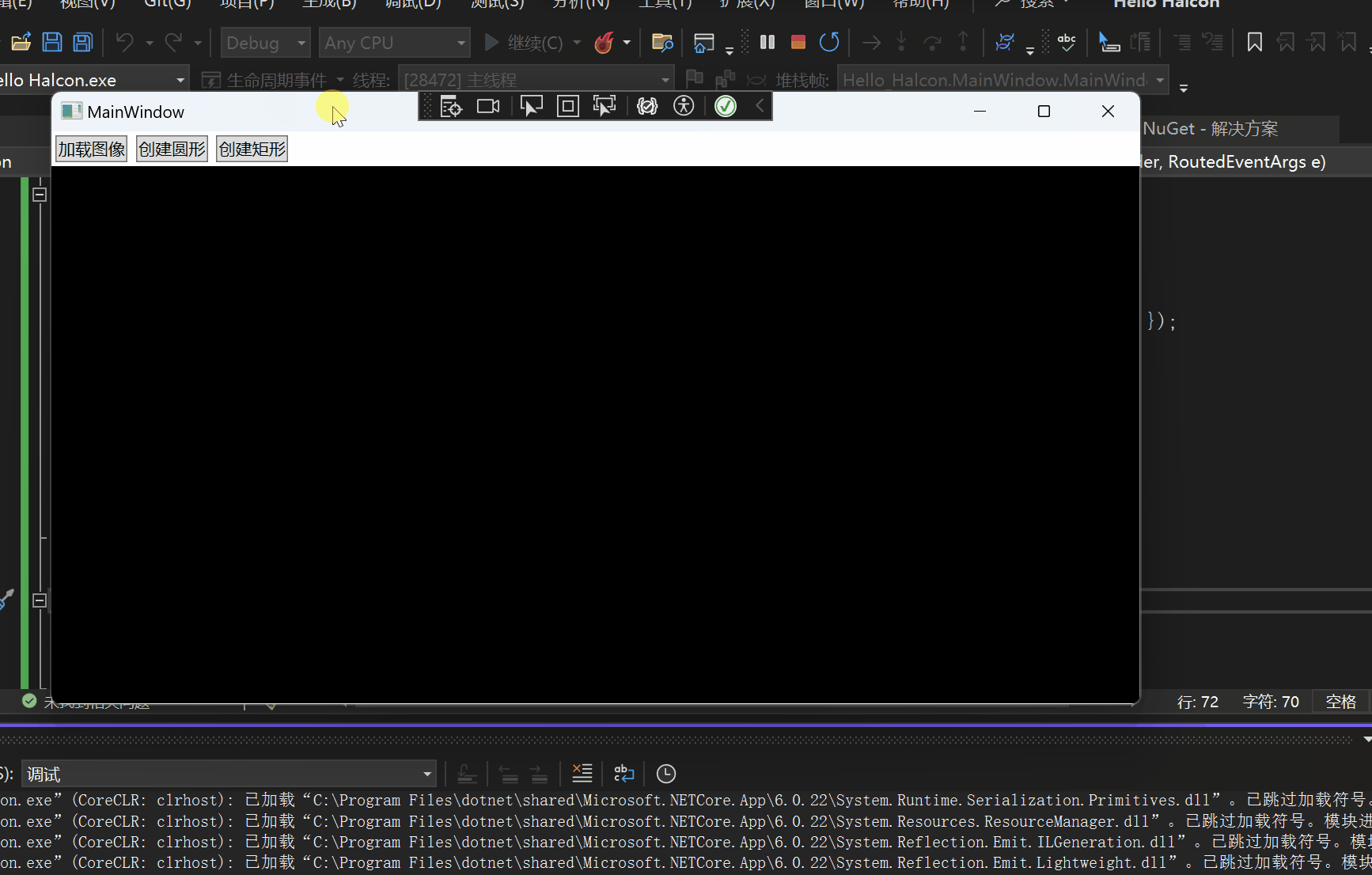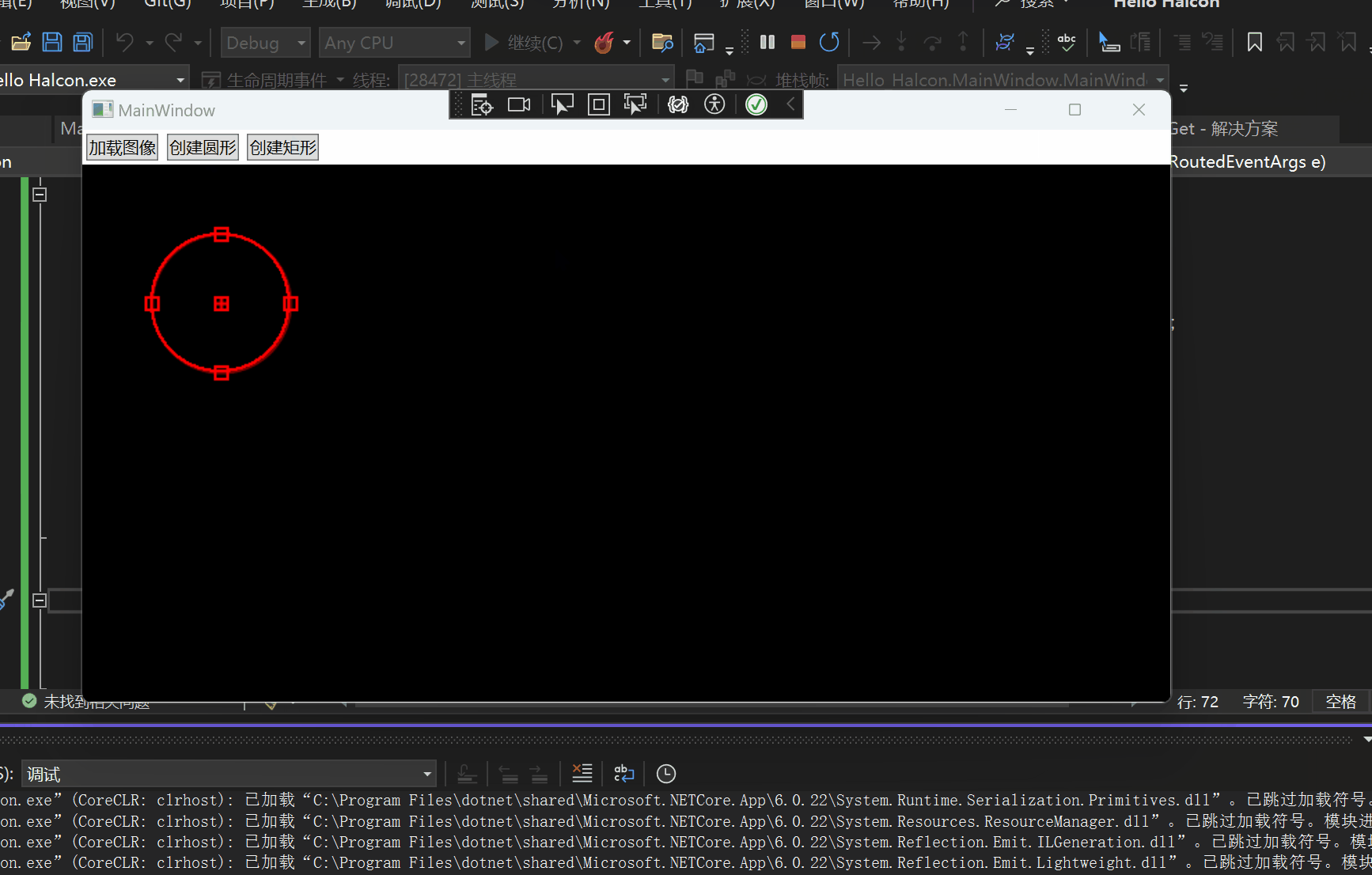
Halcon WPF 开发学习笔记:HSmartWindowControlWPF正常加载
文章目录 加载问题相关文章彻底解决 加载问题 我们在WPF中使用Halcon的时候,会出现图片被拉伸的问题,需要拖动才可以解决,我网上找了好久,终于找到了如何成功解决这个问题。 相关文章 3.7 Halcon 窗体显示对象消失问题 【halcon】…...
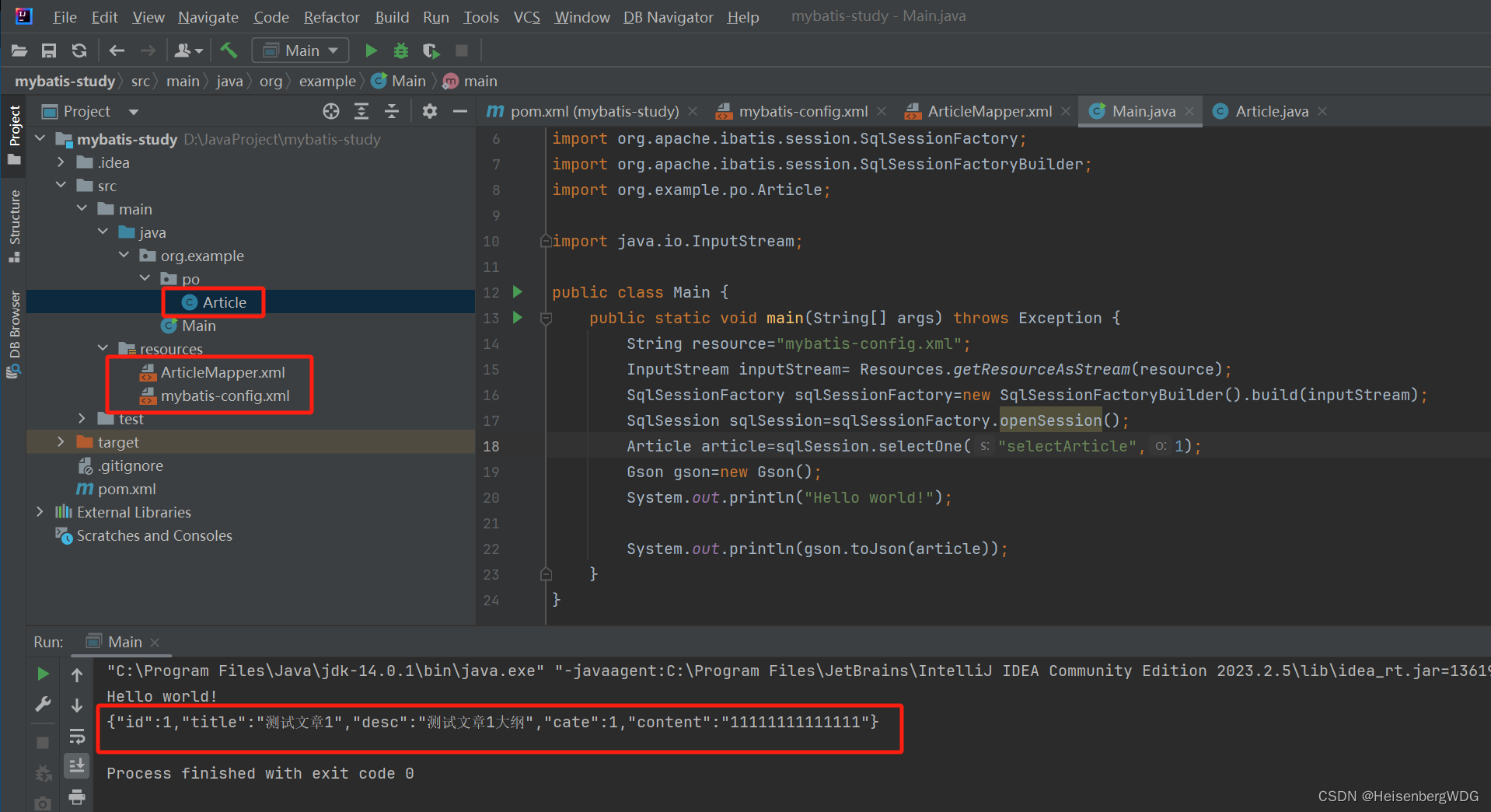
mybatis的简单教程
整体就是mysql里存了一张表,然后在java程序里用mybatis把数据读出来的一个简单示例。 库 blog里有一张表 article 整个项目就是增加了这3个文件 首先是mybatis-config.xml文件 <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE c…...

数据结构 队列(C语言实现)
目录 1.队列的概念及结构2.队列的代码实现 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂,风趣幽默,忍不住分享一下给大家。 点击跳转到网站。 1.队列的概念及结构 队列:只允许在…...
Android---屏幕适配的处理技巧
在几年前,屏幕适配一直是困扰 Android 开发工程师的一大问题。但是随着近几年各种屏幕适配方案的诞生,以及谷歌各种适配控件的推出,屏幕适配也显得越来越容易。下面,我们就来总结一下关于屏幕适配的那些技巧。 ConstraintLayout …...
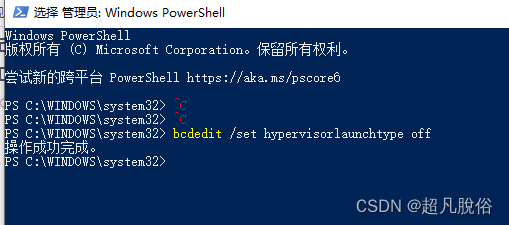
vmware workstation 与 device/credential guard 不兼容
VM虚拟机报错 vmware虚拟机启动时报错:vmware workstation 与 device/credential guard 不兼容: 系统是win10专业版,导致报错原因最终发现是安装了docker,docker自带下载虚拟机Hyper-V,而导致vmware workstation 与 …...

第7章-使用统计方法进行变量有效性测试-7.2.1-单因素方差分析
目录 7.2 方差分析 7.2.1 单因素方差分析 组内变异 组间变异 总变异 随机误差...
黑客技术-小白学习手册
一、黑客是什么 原是指热心于计算机技术,水平高超的电脑专家,尤其是程序设计人员。但后来,黑客一词已被用于泛指那些专门利用电脑网络搞破坏或者恶作剧的家伙。 二、学习黑客技术的原因 其实,网络信息空间安全已经成为海陆空之…...
用示波器测量高压电
示波器本身是不可以测试几千v的高压电电路的,一般自带的探头衰减倍数不够,需要使用高压差分探头或者高压探棒,将测试信号衰减到合适的范围再接入示波器。 普通探头能测差分电压吗?差分探头和普通探头有什么区别?全网最…...

AQS中Node状态
在AQS(AbstractQueuedSynchronizer)中,Node 是一个用于构建等待队列的节点类,用于表示等待获取锁的线程。Node 的状态在不同的同步器中有不同的含义,但一般来说,Node 的状态可以分为以下几种: C…...

STM32 寄存器配置笔记——GPIO配置输出
一、概述 本文主要介绍GPIO 作为输出时的寄存器配置。包括时钟配置,输出模式配置。以STM32F10xxx系列为例,配置PA8、PD2端口作为输出,输出高/低电平。 二、配置流程 1)GPIO外设时钟 通过查找STM32F10xxx中文参考手册得知…...
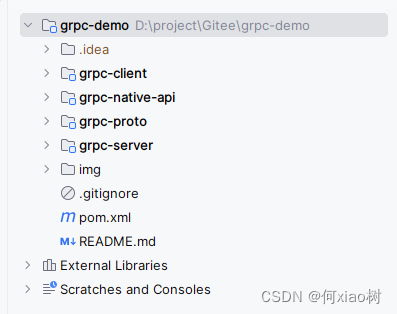
Spring boot 整合grpc 运用
文章目录 GRPC基础概念:Protocol Buffers:proto 基础语法:调用类型: Spring boot 整合 grpc项目结构:整合代码:父 pomproto 模块服务端:客户端:实际调用: 原生集成 GRPC基…...

C++ 模板保姆级详解——template<class T>(什么是模板?模板分哪几类?模板如何应用?)
目录 一、前言 二、 什么是C模板 💦泛型编程的思想 💦C模板的分类 三、函数模板 💦函数模板概念 💦函数模板格式 💦函数模板的原理 💦函数模板的实例化 🍎隐式实例化 🍉显式实…...
uni.getLocation() 微信小程序 线上获取失败
开发版,体验版,用此方法都可以正确获取定位,但是在小程序的线上,总是获取失败 参考:uni-app微信小程序uni.getLocation获取位置;authorize scope.userLocation需要在app.json中声明permission;小程序用户拒绝授权后重新授权-CSDN博客 uniapp 中的 uni.…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
