POJ 3254 Corn Fields 状态压缩DP(铺砖问题)
一、题目大意
我们要在N * M的田地里种植玉米,有如下限制条件:
1、对已经种植了玉米的位置,它的四个相邻位置都无法继续种植玉米。
2、题目中有说一些块无论如何,都无法种植玉米。
求所有种植玉米的方案数(不种植也是一种方案)
二、解题思路
不难看出本题目是铺砖问题,我们可以先写一个基于递归解决的Domo。
可以定义数组color[i][j]代表该位置是否起初就无法种植
并定义数组used[i][j]代表该位置是否已经被旁边的块覆盖,无法种植。
对于i j 位置,判断它如果不能种植,就直接计算下一个位置。
如果可以种植,则分别尝试种植和不种植两种情况,将计算出的方案数求和。
写出递归代码如下:
int rec(int i, int j)
{if (i == n){return 1;}if (j == m){return rec(i + 1, 0);}if (color[i][j] || used[i][j]){return rec(i, j + 1);}int res = 0;bool rt = false, dn = false;if (j + 1 < m){rt = used[i][j + 1];}if (i + 1 < n){dn = used[i + 1][j];}res += rec(i, j + 1);used[i][j] = true;if (j + 1 < m){used[i][j + 1] = true;}if (i + 1 < n){used[i + 1][j] = true;}res += rec(i, j + 1);used[i][j] = false;if (j + 1 < m){used[i][j + 1] = rt;}if (i + 1 < n){used[i + 1][j] = dn;}return res;
}这个递归代码一定是超时的,那么接下来考虑如何把它转成DP,我们发现这个递归算法是从左上一直算到右下,那么对于i j位置,其实只需要记录 (row==i+1&&col<j)和(row==i&&col>=j)的一排元素是否可以种植玉米即可,如下图所示。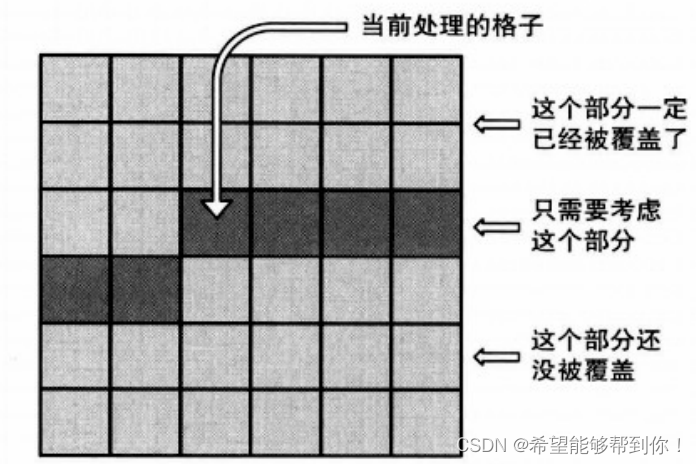
所以不难看出,对于同一个位置,且这一排元素确定时,算出的方案数也是确定的,那么我们就可以从右下角开始,一点点边计算边循环到左上角。
在这个计算的过程中,和递归一样,只需要考虑两点。
第一,如果i j位置不能种植玉米,则加上i j位置不种植时的下一块的值 crt[ S 去掉第 j 块 ]。
第二,如果i j位置能够种植玉米,则依次加上i j位置种植和不种植情况时下一块的值,dp[S] 和 crt[S 加上第 j 块 和 第 j+1 块](如果j+1==m,则不用添加第j+1块)。
初始化时,考虑到最后一块的情况,如果它能够种植,则是2,如果不能则是1,那么就可以初始化DP数组上一行的所有元素为1。
可以使用滑动数组求解,循环计算每一块,之后本次的当前行作为下次计算的上一行即可。
最终输出的答案为上一行的第一个位置。
三、代码
#include <iostream>
using namespace std;
const int MAX_M = 12;
const int MAX_N = 12;
int dp[2][1 << MAX_M];
bool color[MAX_N][MAX_M];
int n, m;
void solve()
{int *crt = dp[0], *next = dp[1];fill(crt, crt + (1 << MAX_M), 1);for (int i = n - 1; i >= 0; i--){for (int j = m - 1; j >= 0; j--){for (int used = 0; used < (1 << m); used++){if (color[i][j] || (used >> j & 1)){next[used] = crt[used & ~(1 << j)];}else{int res = crt[used];if (j + 1 < m){res += crt[used | (1 << (j + 1)) | (1 << j)];}else{res += crt[used | (1 << j)];}next[used] = res % 100000000;}}swap(next, crt);}}printf("%d\n", crt[0]);
}
int main()
{scanf("%d%d", &n, &m);int num;for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){scanf("%d", &num);color[i][j] = num == 0;}}solve();return 0;
}四、相关文献
《挑战程序设计竞赛(第二版)》P196-P198 铺砖问题
相关文章:

POJ 3254 Corn Fields 状态压缩DP(铺砖问题)
一、题目大意 我们要在N * M的田地里种植玉米,有如下限制条件: 1、对已经种植了玉米的位置,它的四个相邻位置都无法继续种植玉米。 2、题目中有说一些块无论如何,都无法种植玉米。 求所有种植玉米的方案数(不种植也…...
transformers安装避坑
1.4 下载rust编辑器 看到这里你肯定会疑惑了,我们不是要用python的吗? 这个我也不知道,你下了就对了,不然后面的transformers无法安装 因为是windows到官网选择推荐的下载方式https://www.rust-lang.org/tools/install。 执行文…...
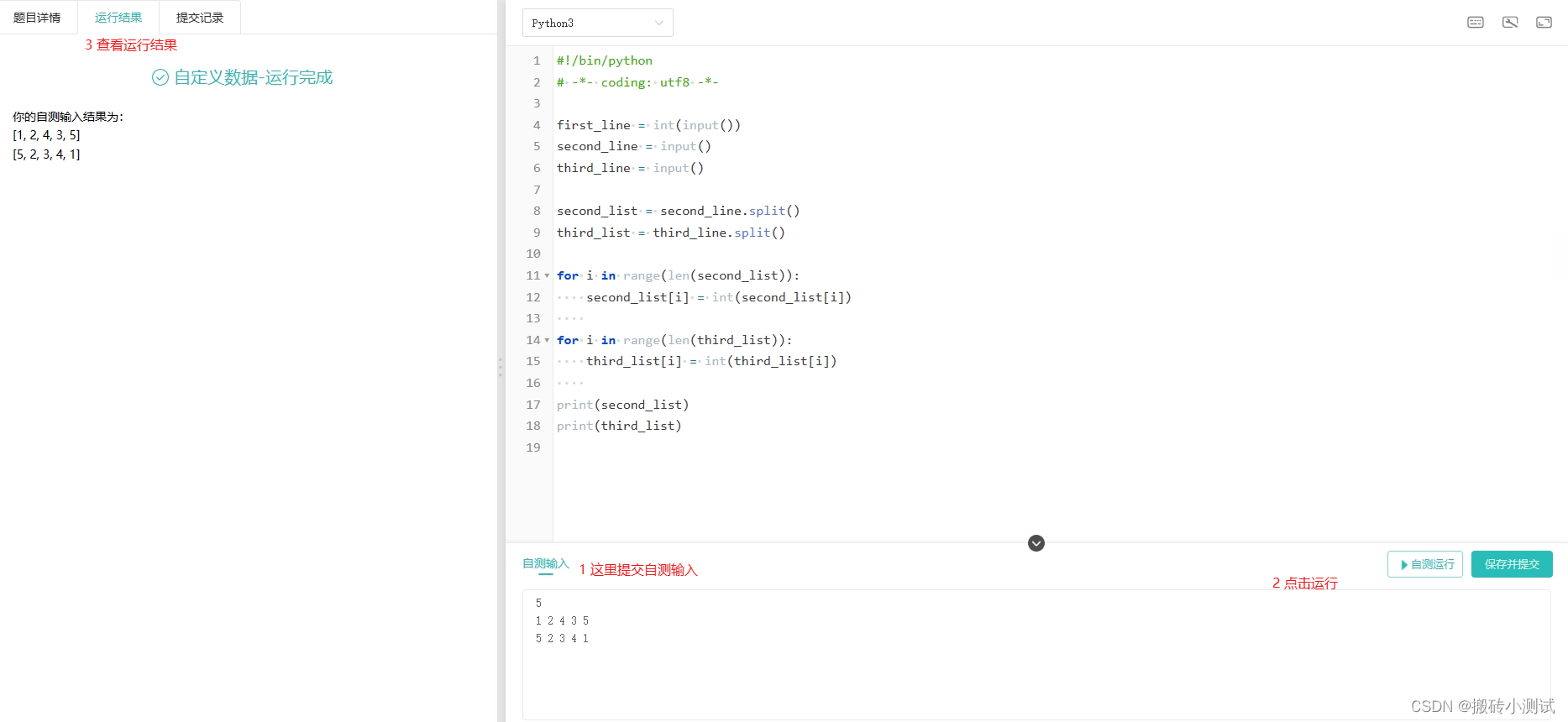
牛客、赛码网OJ调试(全)
现在无论开发还是测试,面试的时候都需要考察代码能力。 从测试的职业发展来看,现在市场上对于纯功能测试的需求很少,招聘方均要求面试者一方面具备测试基础能力,也要求有点代码能力。 对于测试来说,除了测试开发&#…...

【CSS】全局声明引入自定义字体
以下用vue项目为例,其他的也是类似! 在Vue.js中可以使用全局样式表来定义字体。通常,可以在项目中的主样式表中定义全局字体,然后确保该样式表在整个应用程序中被引入。 以下是一般的步骤: 在项目中创建一个全局样式…...

「Flask」路由+视图函数
路由 路由的作用是将 HTTP 请求的 URL 路径映射到相应的函数处理程序。这样我们在开发过程中,就能将不同的 URL 路径与相应的函数处理程序关联起来,从而实现对 Web 应用的灵活控制。 路由可以分为静态路由和动态路由。两者主要是在形式上有一些区别&am…...

信息系统项目管理师 教材目录、考试大纲、考情
文章目录 考情考试大纲第1章 信息化发展第2章 信息技术发展第3章 信息系统治理第4章 信息系统管理第5章 信息系统工程第6章 项目管理概论第7章 项目立项管理第8章 项目整合管理第9章 项目范围管理272第10章 项目进度管理297第11章 项目成本管理334第12章 项目质量管理358第13章…...

python线性回归实现
import random import torch# ①根据带有噪声的线性模型构造一个人造数据集。 使用线性模型参数w[2,−3.4] b4.2和噪声项ϵ生成数据集及其标签 def synthetic_data(w, b, num_examples):"""生成 y Xw b 噪声。"""# 生成均值为0,标…...
【JavaEESpring】认识Spring
认识Spring 1. 什么是框架2. SpringBoot 介绍2.1 Spring 的介绍2.2 SpringBoot 1. 什么是框架 框架(Framework) ,意思是框架、机制、准则。通俗的来讲: 框架是实现某种功能的半成品, 他提供了⼀些常⽤的⼯具类, 我们在框架的基础上, 可以更加⾼效的进⾏开发 后端框…...
)
Rust逆向学习 (5)
文章目录 Reverse for Vecvec! 与 添加元素元素访问元素遍历枚举数组弹出最后一个元素——pop 总结 本文将对Rust中的通用集合类型——动态数组 Vec进行学习,对应参考书中的第8章。 Reverse for Vec Vec是Rust中的动态数据结构,与C中的vector功能类似。…...
)
89.STL-函数对象的使用(仿函数)
目录 1.什么是函数对象 2.仿函数示例 3.代码示例 1.什么是函数对象 函数对象是C中的一种编程概念,也称为函数符或仿函数。其实就是重载“()”操作符,使得类对象可以像函数那样调用。 分类:假定某个类有一个重载的operator(),而且重载的oper…...
文件管理技巧:按文件容量大小分类,自动移动至目标文件夹的方法
按文件容量大小分类可以帮助快速识别和筛选出不同大小的文件。这样做有很多好处。首先,可以轻松地查找和访问特定大小的文件,提高工作效率。其次,通过将不同大小的文件分类,可以更好地了解和掌控文件的使用情况,避免存…...
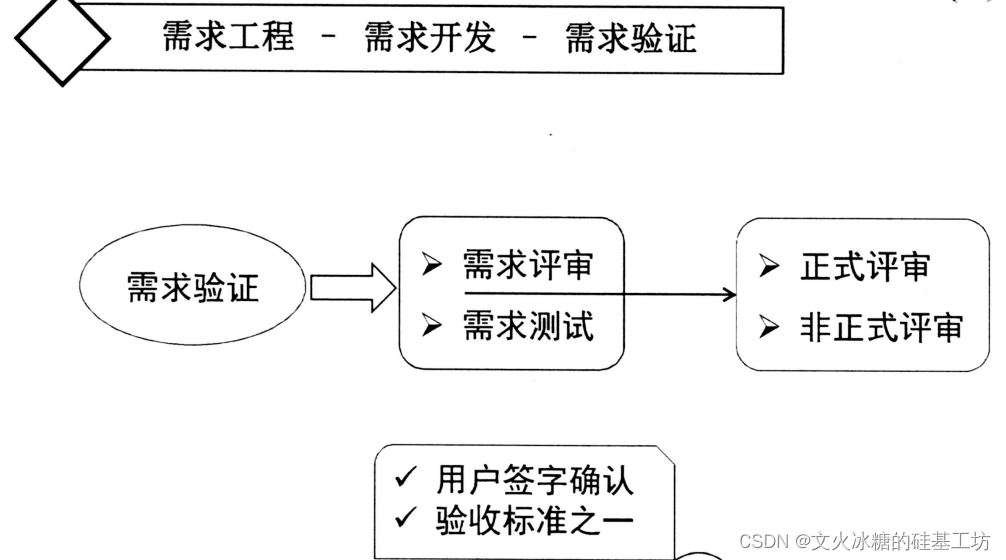
[架构之路-246]:目标系统 - 设计方法 - 软件工程 - 需求工程- 需求开发:获取、分析、定义、验证
目录 前言: 架构师为什么需要了解需求分析 一、需求工程概述 1.1 概述 1.2 需求工程的两大部分 (1)需求开发:系统工程师的职责、目标系统开发角度 (2)需求管理:项目管理者的职责、项目管…...
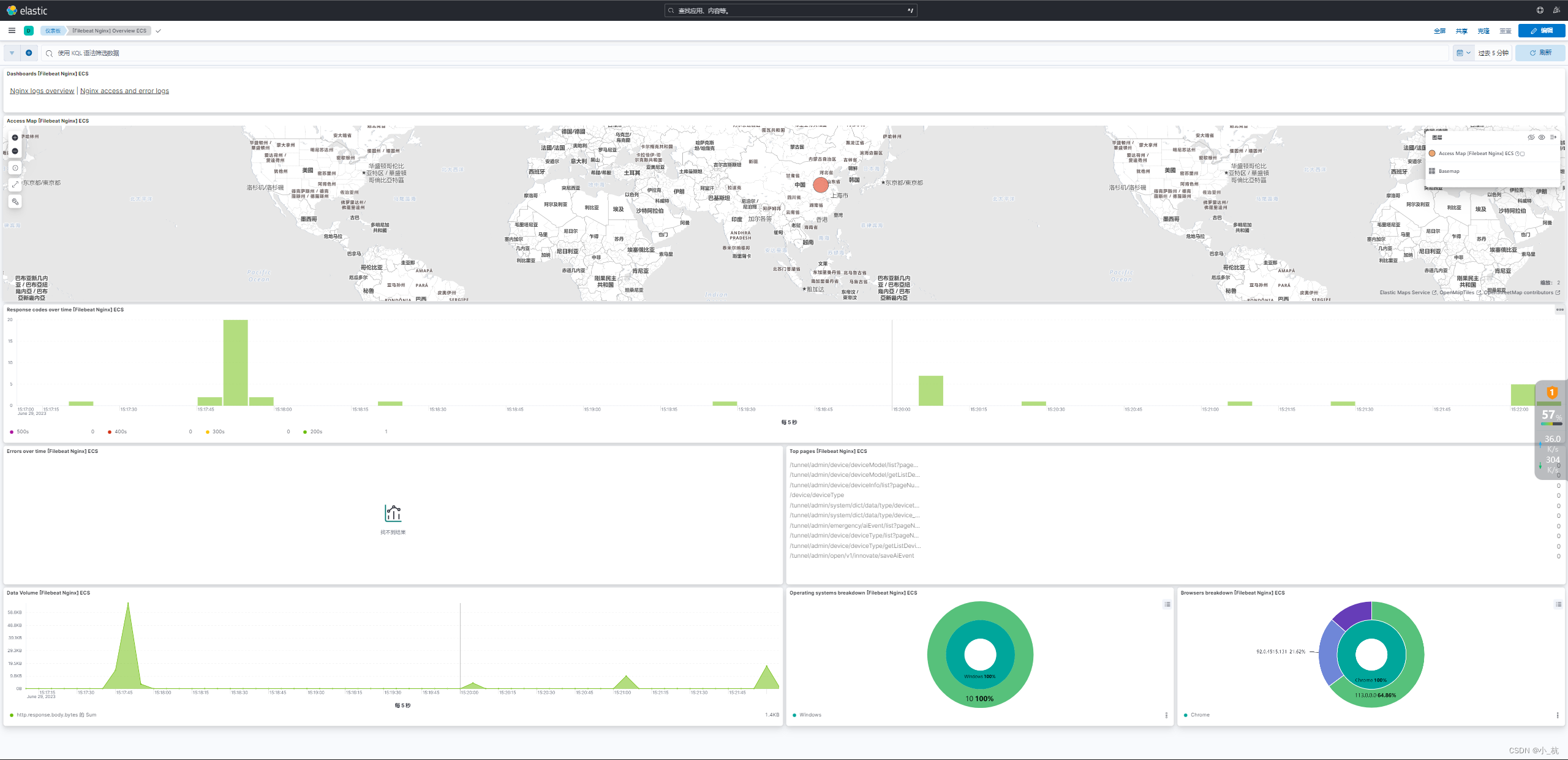
轻量日志管理方案-[EFK]
使用FileBeat进行日志文件的数据收集,并发送到ES进行存储,最后Kibana进行查看展示; 这个应该是最简单,轻量的日志收集方案了。 最总方案为:FileBeatESKibana ; 【Kibana过于强大,感觉可以无限扩展】 文章目…...
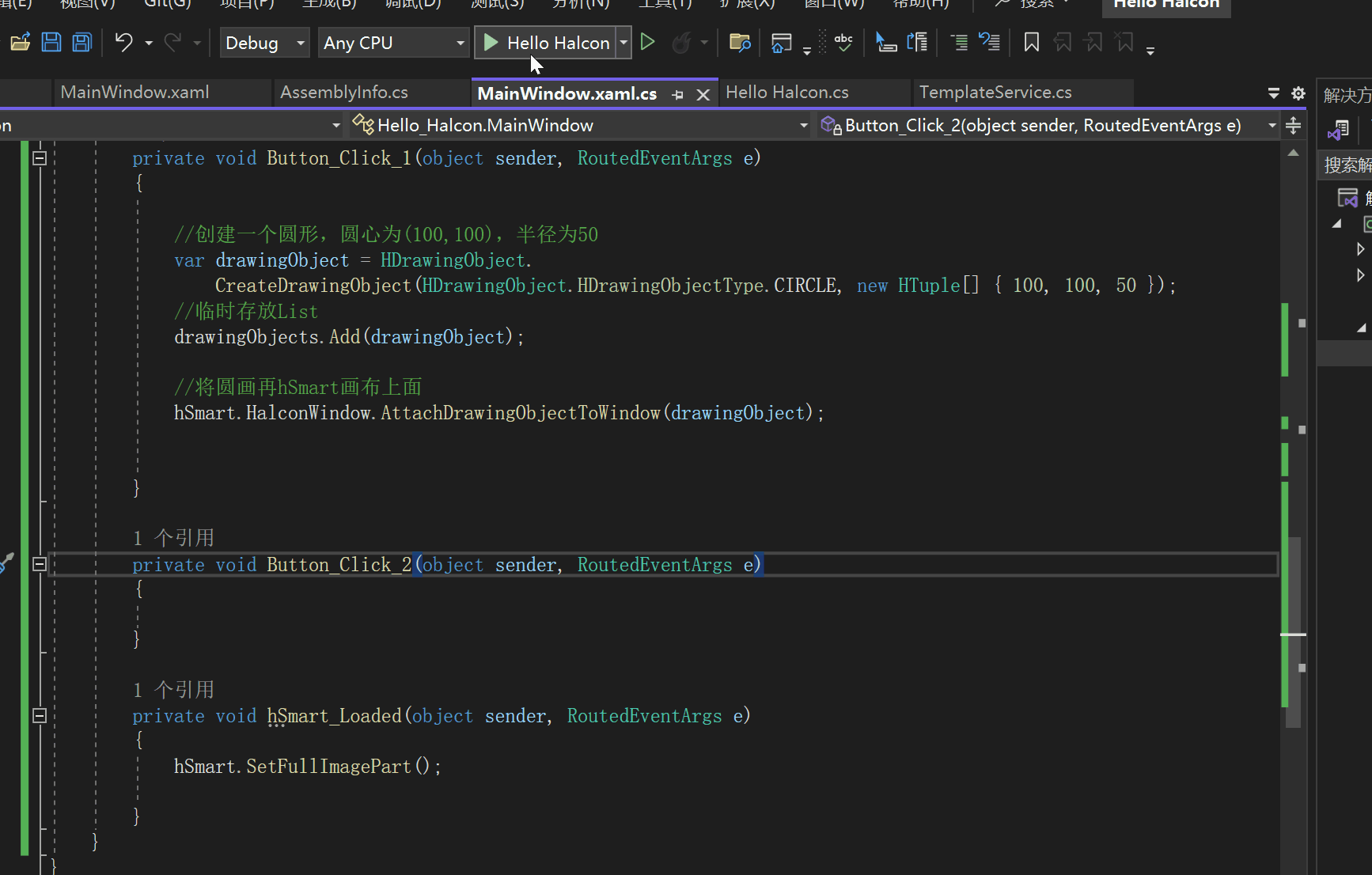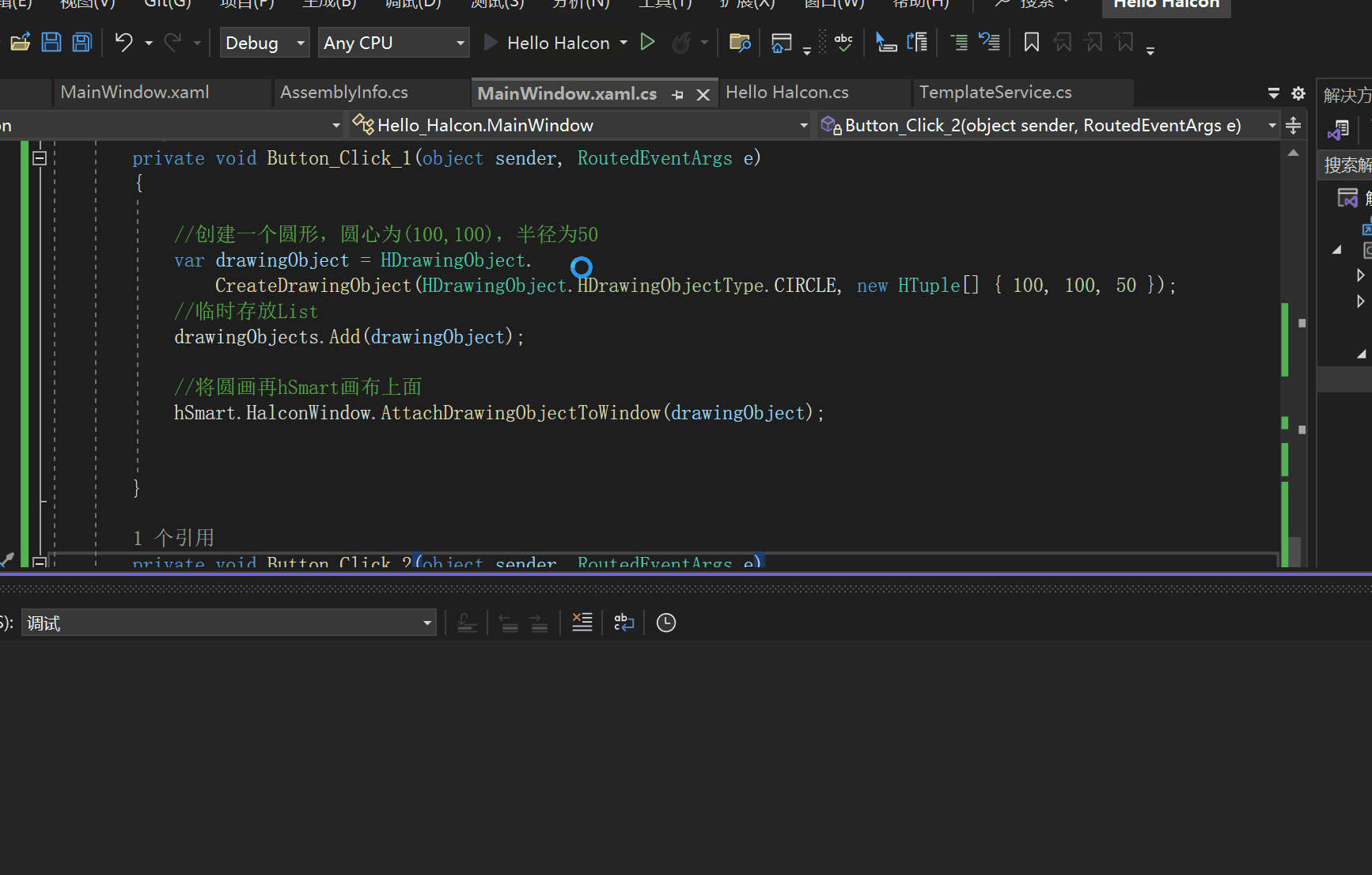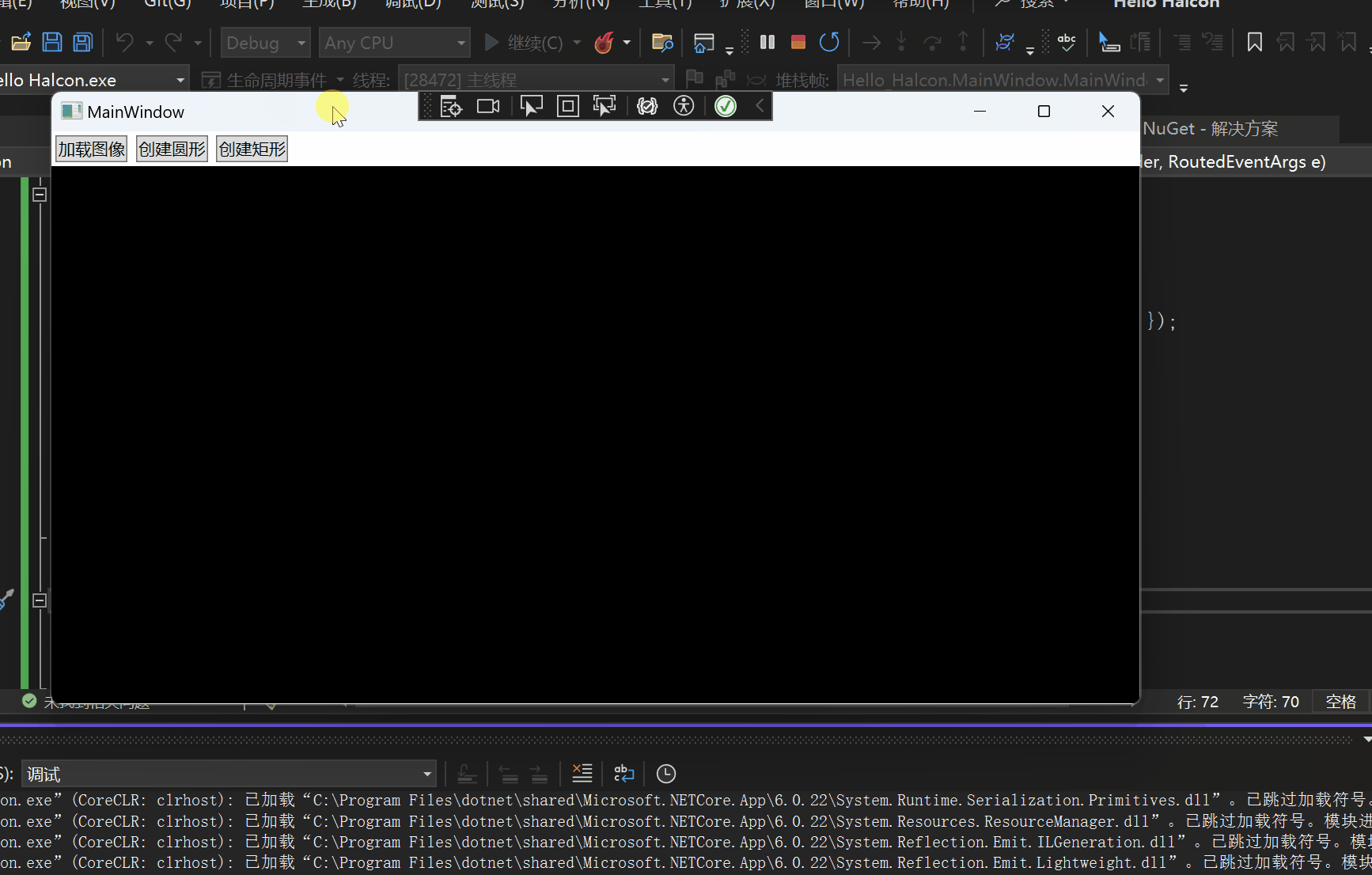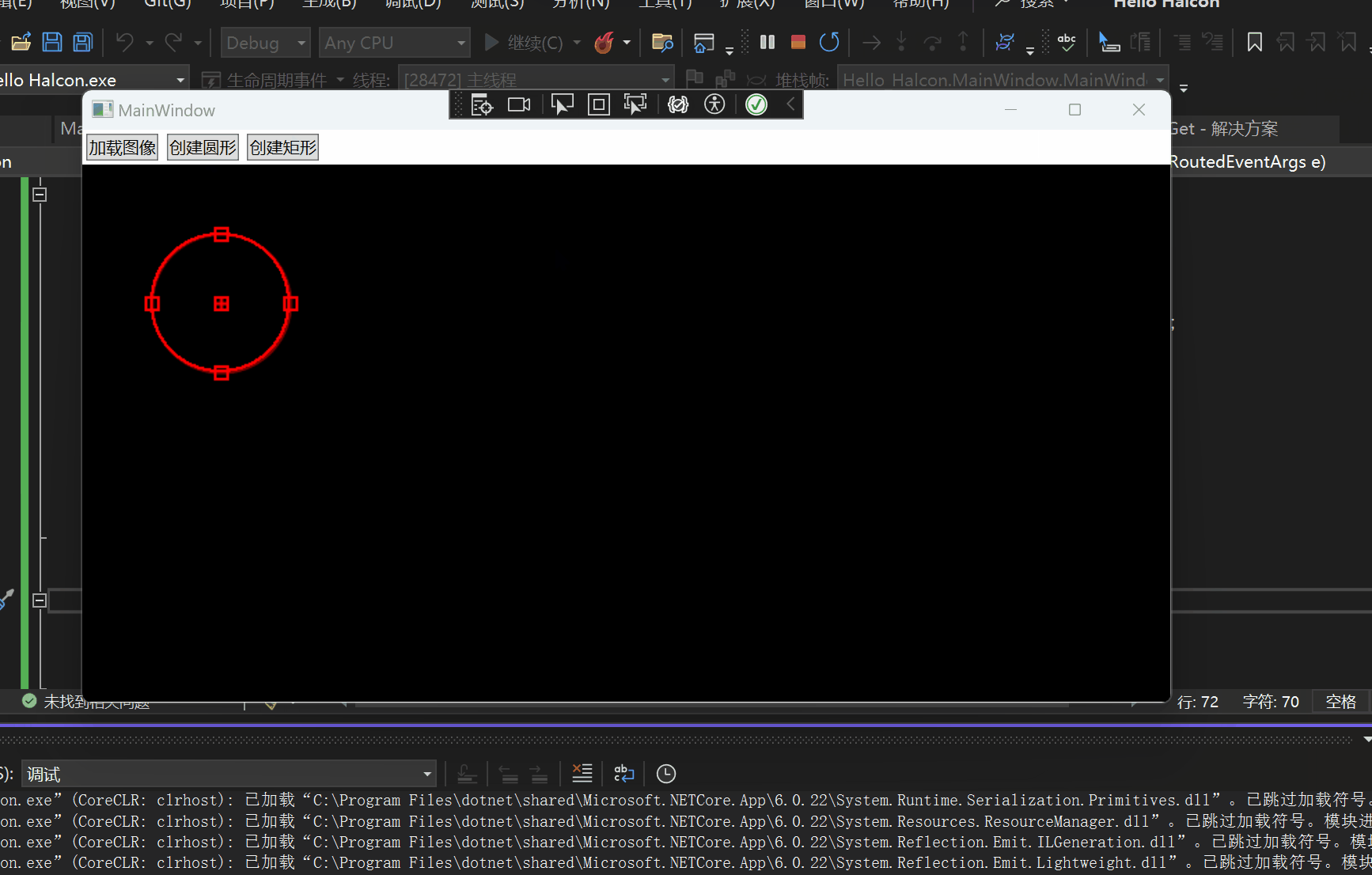
Halcon WPF 开发学习笔记:HSmartWindowControlWPF正常加载
文章目录 加载问题相关文章彻底解决 加载问题 我们在WPF中使用Halcon的时候,会出现图片被拉伸的问题,需要拖动才可以解决,我网上找了好久,终于找到了如何成功解决这个问题。 相关文章 3.7 Halcon 窗体显示对象消失问题 【halcon】…...
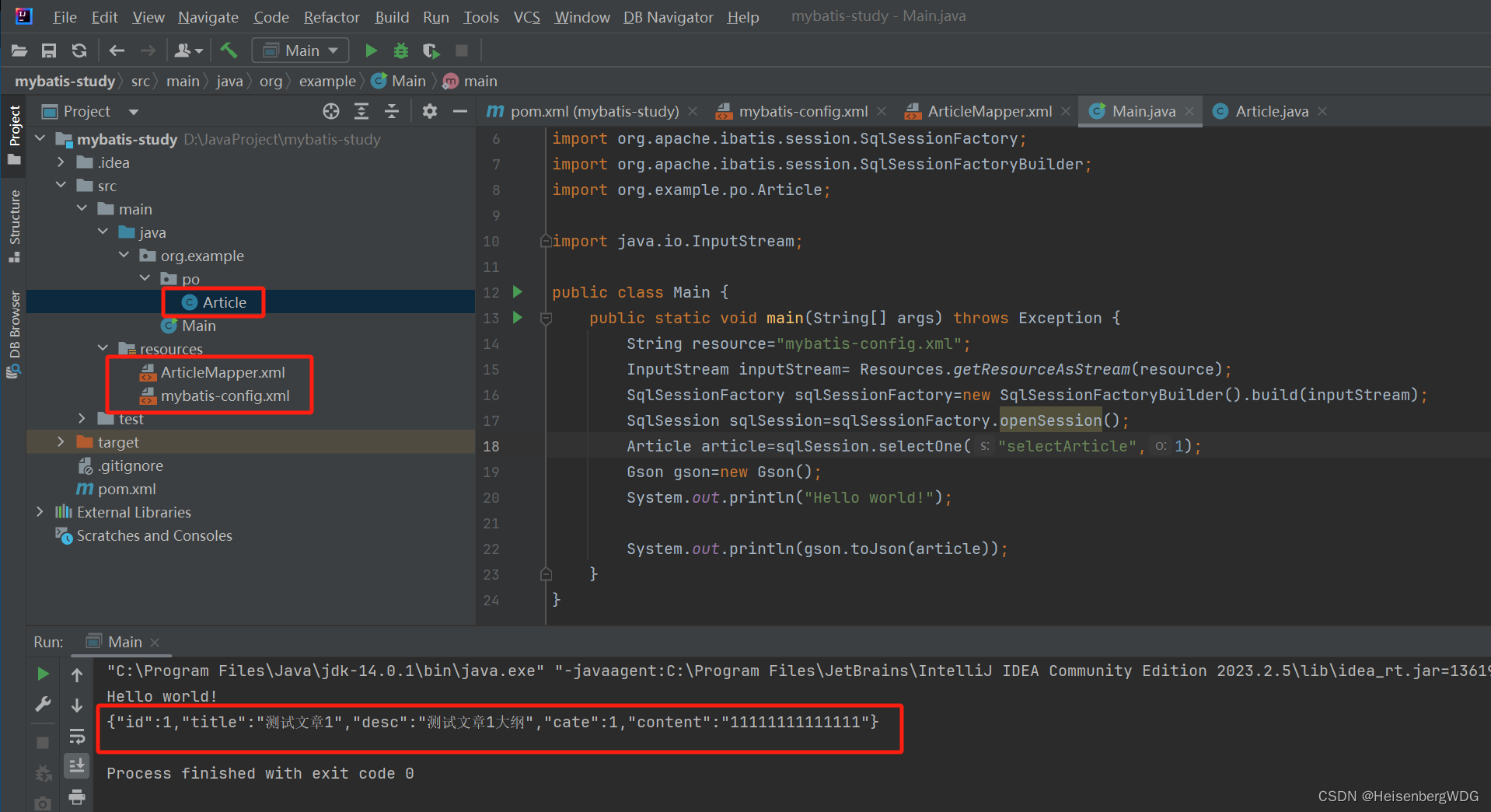
mybatis的简单教程
整体就是mysql里存了一张表,然后在java程序里用mybatis把数据读出来的一个简单示例。 库 blog里有一张表 article 整个项目就是增加了这3个文件 首先是mybatis-config.xml文件 <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE c…...

数据结构 队列(C语言实现)
目录 1.队列的概念及结构2.队列的代码实现 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂,风趣幽默,忍不住分享一下给大家。 点击跳转到网站。 1.队列的概念及结构 队列:只允许在…...
Android---屏幕适配的处理技巧
在几年前,屏幕适配一直是困扰 Android 开发工程师的一大问题。但是随着近几年各种屏幕适配方案的诞生,以及谷歌各种适配控件的推出,屏幕适配也显得越来越容易。下面,我们就来总结一下关于屏幕适配的那些技巧。 ConstraintLayout …...
vmware workstation 与 device/credential guard 不兼容
VM虚拟机报错 vmware虚拟机启动时报错:vmware workstation 与 device/credential guard 不兼容: 系统是win10专业版,导致报错原因最终发现是安装了docker,docker自带下载虚拟机Hyper-V,而导致vmware workstation 与 …...

第7章-使用统计方法进行变量有效性测试-7.2.1-单因素方差分析
目录 7.2 方差分析 7.2.1 单因素方差分析 组内变异 组间变异 总变异 随机误差...
黑客技术-小白学习手册
一、黑客是什么 原是指热心于计算机技术,水平高超的电脑专家,尤其是程序设计人员。但后来,黑客一词已被用于泛指那些专门利用电脑网络搞破坏或者恶作剧的家伙。 二、学习黑客技术的原因 其实,网络信息空间安全已经成为海陆空之…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
