论文笔记:Deep Trajectory Recovery with Fine-Grained Calibration using Kalman Filter
TKDE 2021
1 intro
1.1 背景
- 用户轨迹数据对于改进以用户为中心的应用程序很有用
- POI推荐
- 城市规划
- 路线规划
- 由于设备和环境的限制,许多轨迹以低采样率记录
- 采样的轨迹无法详细说明物体的实际路线
- 增加了轨迹中两个连续采样点之间的不确定性
- ——>开发有效的算法以基于原始低采样数据恢复高质量轨迹非常重要
- 总的来说,轨迹恢复任务在两种不同的环境中被研究,这取决于地图信息(如道路网络)是否可用
- 在第一种环境中,轨迹位置通常映射到道路段或POI
- 在第二种环境中,地图信息作为输入是不可用的,称之为自由空间轨迹恢复
- 本文关注的是第二种环境
1.2 之前的工作
- 现有研究中存在两个潜在问题
- 许多方法依赖于启发式搜索算法或简单的概率模型
- 主要模拟位置之间的相邻过渡模式
- 深度优先搜索算法
- 吸收马尔可夫链
- 吉布斯抽样
- 这些方法不能很好地捕获复杂的顺序依赖性或全局数据相关性
- 主要模拟位置之间的相邻过渡模式
- 为了减少无约束数值坐标的预测复杂性,大多数以前的研究采用了一个常见的预处理策略——将空间映射到离散单元,例如单元格或锚点
- 然后,他们的焦点变成如何在离散单元上开发有效的恢复算法
- 使用离散单元可能会带来噪音或不准确的信息
- 因此,通常需要一个后校准步骤来产生更准确的结果
- 然而,以前的方法主要采用简单的启发式校准方法,例如识别单元格中的频繁位置或简单地使用单元格的中心坐标
- 忽视了后校准在细化粗糙单元级预测结果中的重要性
- 许多方法依赖于启发式搜索算法或简单的概率模型
- 深度学习任务(如RNN)
- 只专注于局部时间窗口内的下一步或短期位置预测
- 仍直接产生单元格级的预测,并没有在他们的模型中结合原则性的后校准组件来得出更准确的估计
- ——>将现有的基于神经网络的轨迹模型直接应用于自由空间轨迹恢复任务是困难的
1.3 本文贡献
- 提出了一种新颖的深度混合轨迹恢复模型(DHTR)
- 子序列到序列恢复模型(即subseq2seq)
- 扩展了seq2seq
- 为了有效捕获全局时空相关性,采用了空间和时间注意力机制来增强模型性能
- 通过注意力机制,我们的模型能够表征轨迹点之间的长距离相关性
- 将subseq2seq组件与卡尔曼滤波器(KF)整合在一起,以校准噪声单元预测为准确坐标
- 在每一个时间步,来自subseq2seq组件的噪声预测将被送入KF组件进行校准
- 然后精炼的预测将被转发到subseq2seq组件,用于下一个时间步的计算
- 子序列到序列恢复模型(即subseq2seq)
- ——>模型具有两个组件的优点
- 建模复杂序列数据的能力
- 降低预测噪声的能力
2 Preliminary
2.1 一些概念
- 位置
- 经纬度坐标<x,y>
- 区域单元
- 整个地理空间被划分为一组区域单元,用C表示
- 每个单元c∈C是一个边长为l的正方形空间
- 区域单元坐标为中心点的坐标<Xc,Yc>
- 轨迹点
- 一个移动物体的轨迹点是一个带时间戳的位置
- 由一个四元组<x;y;s;c>来建模
- a:x是经度,a:y是纬度,a:s是时间戳,a:c是点a被分配到的单元
- 采样间隔
- 一个移动物体两个连续采样点之间的时间差
- ε-采样轨迹
- 同一移动物体使用采样间隔"的n个均匀采样点的时间有序序列
(后续表述中把上标(t)去掉了)
- ε采样子轨迹
- 给定一个ε采样轨迹t,相应的子轨迹t是t的一个m长度的子序列
- 子轨迹中的位置在时间戳上可能不是均匀分布的
2.2 问题定义
- 给定一个ε采样轨迹数据集和一个子轨迹t‘,我们希望重建或恢复相应的轨迹t。
- 也就是说,对于每个缺失的轨迹点ai(即ai属于t但不属于t‘),我们将推断其在时间ai:s时对应的经度ai:x和纬度ai:y。
3 模型
3.1 模型总览
- 包含三个主要部分
- 第一部分是精心设计的子序列到序列(subseq2seq)神经网络模型
- 在seq2seq的基础上开发的
- 第二部分是一个注意力机制,它用于使subseq2seq能够捕获复杂的时空关联
- 注意力机制同时考虑了整个轨迹中位置之间的空间和时间影响
- 为了减少直接建模数值坐标序列的复杂性,subseq2seq组件在单元级捕获序列注意力相关性
- 第三部分用基于卡尔曼滤波器的新型后校准组件增强了subseq2seq模型
- 将subseq2seq组件和KF组件整合在一个联合的深度混合模型中
- 第一部分是精心设计的子序列到序列(subseq2seq)神经网络模型
3.2 Subseq2seq
- 不是直接预测数值坐标值,而是首先推断缺失轨迹点的对应单元
- 单元ID序列比原始数值序列更可靠且易于建模
- 主要思想是将恢复任务转化为一个序列到序列的任务
- 输入序列是子轨迹,输出序列是重建的完整轨迹
- 输入与相应的输出高度相关
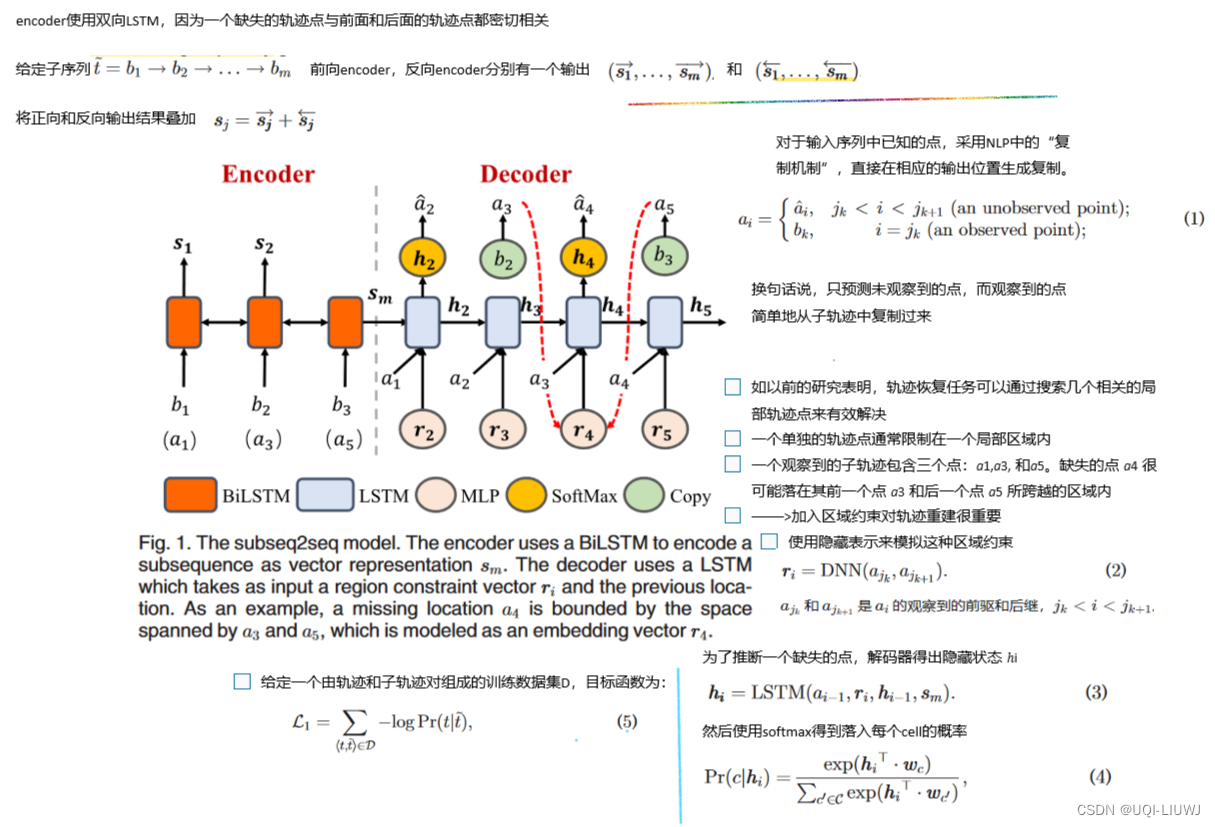
3.3 时空attention
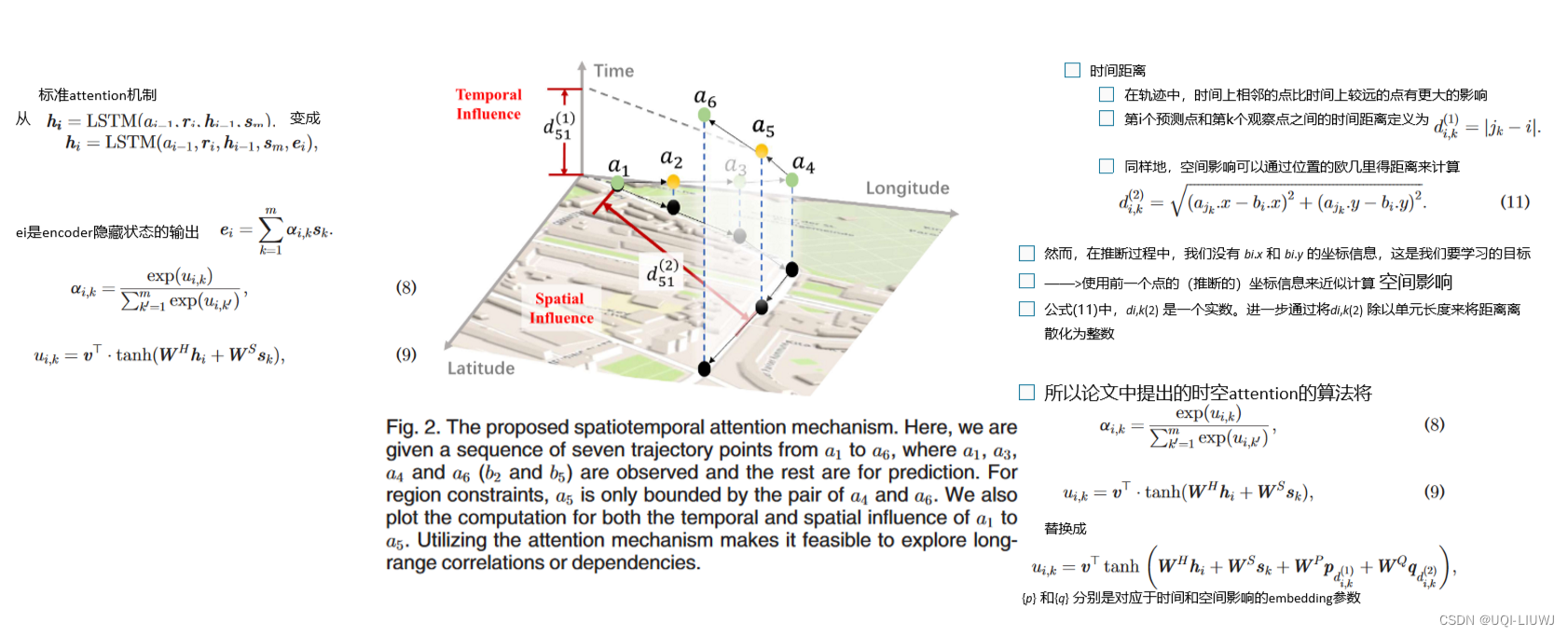
3.4 应用卡尔曼滤波器
【精选】机器学习笔记:卡尔曼滤波_UQI-LIUWJ的博客-CSDN博客
- 之前的方法应用subseq2seq模型来表征轨迹的单元序列,然后将预测单元的中心坐标视为最终预测
- 这种方法有两个潜在的缺点
- 预测模型可能会受到噪声的影响,例如仪器误差
- 由于我们使用对应的单元坐标作为代理,最终的估计是粗略的
- 这种方法有两个潜在的缺点
- ——>提出将上述神经网络模型与卡尔曼滤波器(KF)整合
3.4.1 卡尔曼滤波器
- 卡尔曼滤波器(KFs)通常在线性和高斯噪声的假设下是最优的状态估计器。
- 在KF模型中,使用一个状态向量 gi,它可能包含位置和/或速度,来表示i时刻物体的状态。
- 物体以高斯噪声 eg 线性更新状态gi
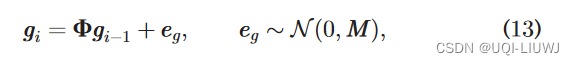
- M是噪声eg的协方差,Φ是状态更新矩阵
- 在KF模型中,真实值 gi 可以通过测量向量 zi 来测量
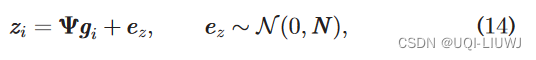
- φ是测量矩阵
- 在KF模型中,测量向量 zi 是可观察的,真实状态 gi 是待估计的未知变量
- 方程(13)和(14)中的矩阵φ,Φ,M,N被视为先验已知的
- KF模型使用两个程序,即预测(Prediction)和更新(Update),来迭代估计 g 的真实值并计算一个协方差矩阵,表示为 H,用以表达 g 的不确定性。
3.4.1.1 预测
在预测过程中,卡尔曼滤波器使用以下方程来预测时i时刻的状态 g 和协方差矩阵 H
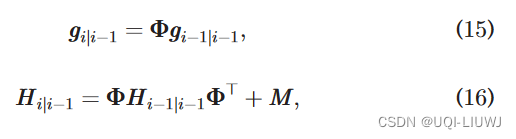
- 下标“i−1∣i−1”表示在i-1时刻由更新程序生成的变量,而下标“i∣i−1”表示预测的状态和协方差。
3.4.1.2 更新
在更新过程中,KF模型使用可观察的测量向量 zi 来更新/校正预测的 gi∣i−1 和 Hi∣i−1 :

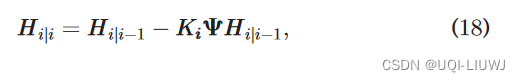
其中,Ki 被称为最优卡尔曼增益,它结合了预测状态和测量状态作为更新状态。
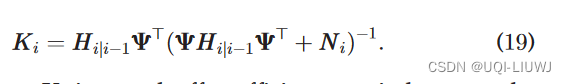
- 我们可以看到 Ki 是估计误差的协方差矩阵 Hi和测量误差的协方差矩阵 Ni 之间的权衡系数矩阵。注意,在标准KF中,协方差矩阵 Ni 是一个预设常数。这里,我们加入了下标i,以便于我们随后的扩展。
- 在每个时间步长i,KF接受噪声测量zi 及其对应的协方差矩阵 Ni作为输入,并产生“过滤”后的测量值
如下:

3.4.2 卡尔曼滤波+subseq2seq
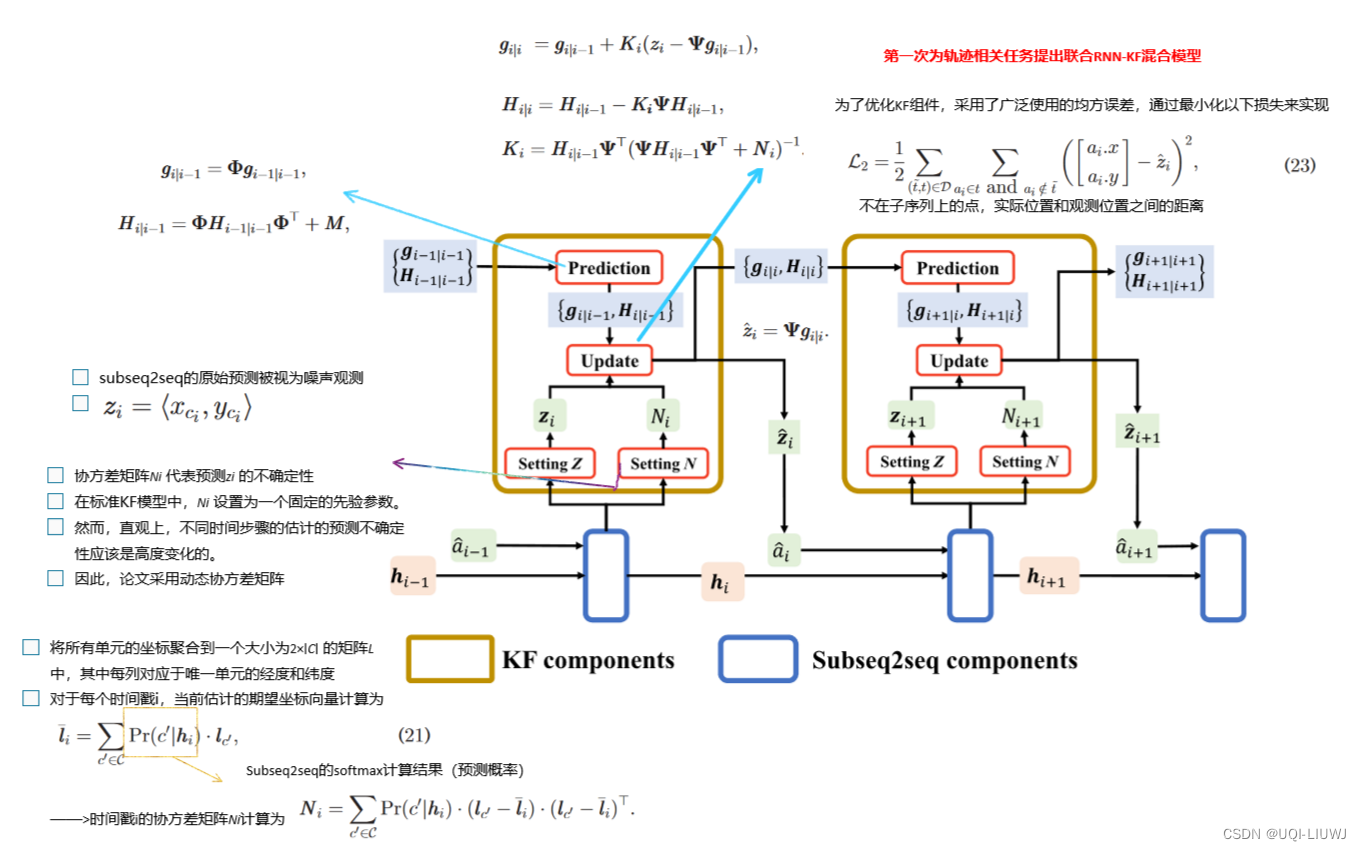
3.5 训练
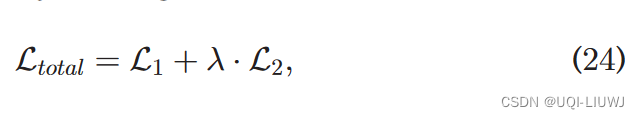
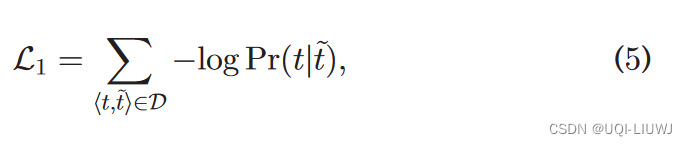
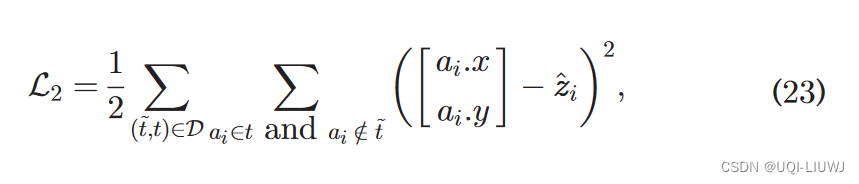
4 实验
4.1 实验数据
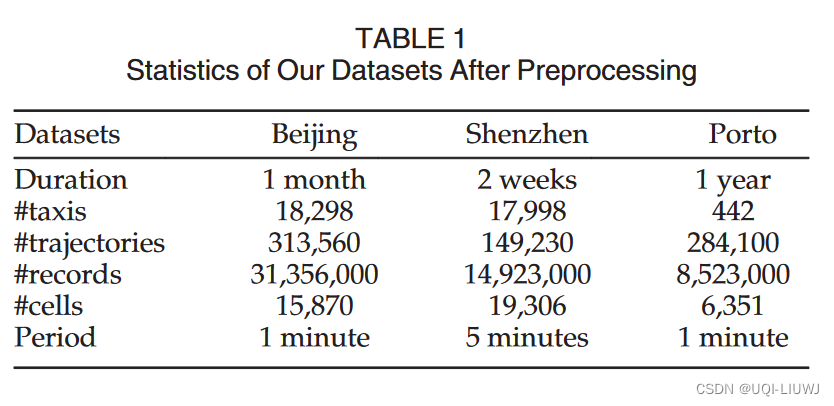
4.2 实验结果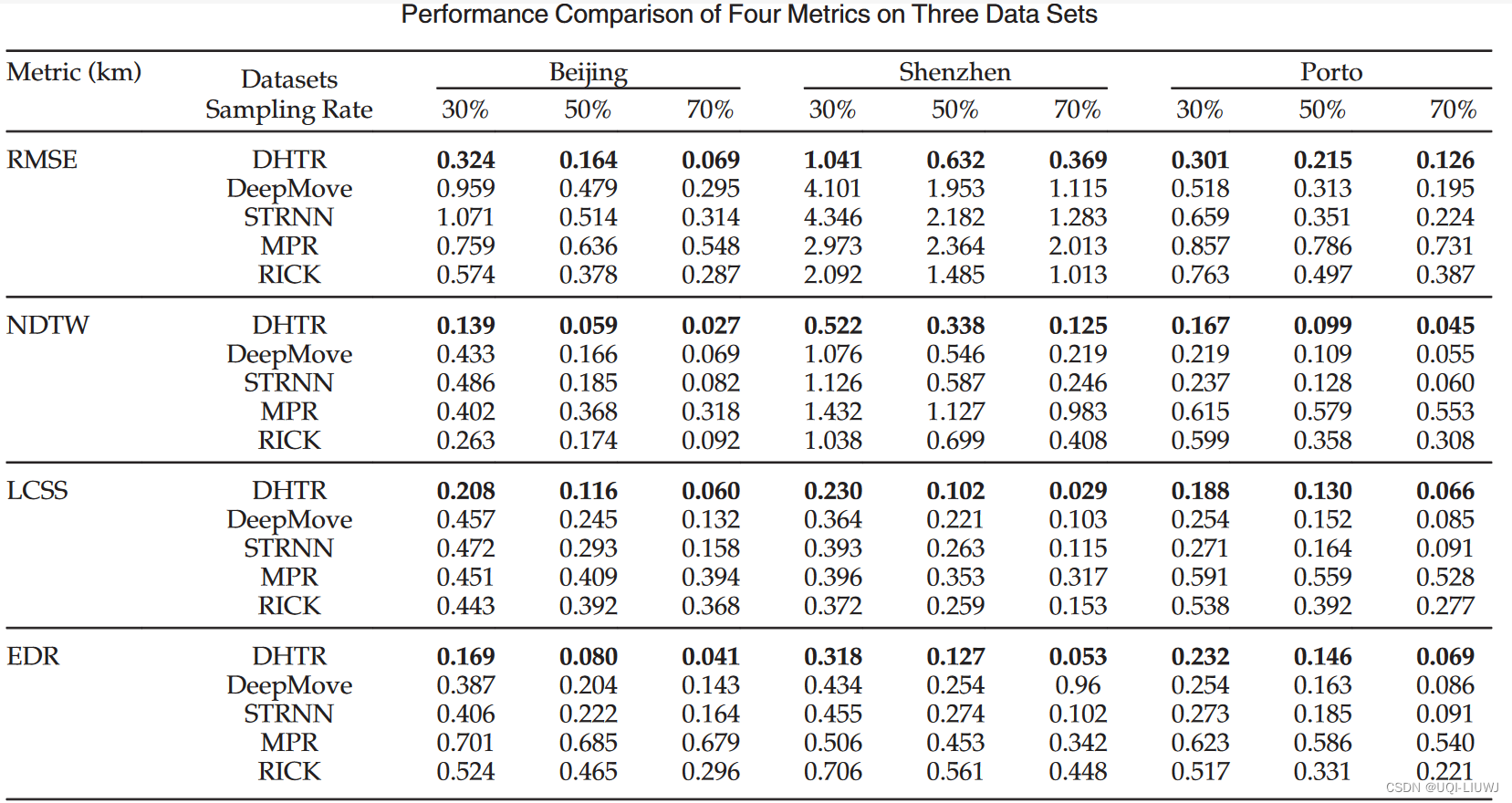

相关文章:

论文笔记:Deep Trajectory Recovery with Fine-Grained Calibration using Kalman Filter
TKDE 2021 1 intro 1.1 背景 用户轨迹数据对于改进以用户为中心的应用程序很有用 POI推荐城市规划路线规划由于设备和环境的限制,许多轨迹以低采样率记录 采样的轨迹无法详细说明物体的实际路线增加了轨迹中两个连续采样点之间的不确定性——>开发有效的算法以…...

ubuntu下tensorrt环境配置
文章目录 一、Ubuntu18.04环境配置1.1 安装工具链和opencv1.2 安装Nvidia相关库1.2.1 安装Nvidia显卡驱动1.2.2 安装 cuda11.31.2.3 安装 cudnn8.21.2.4 下载 tensorrt8.4.2.4 二、编写CMakeLists.txt三、TensorRT系列教程 一、Ubuntu18.04环境配置 教程同样适用与ubuntu22.04…...
网络安全基础之php开发文件下载的实现
前言 php是网络安全学习里必不可少的一环,简单理解php的开发环节能更好的帮助我们去学习php以及其他语言的web漏洞原理 正文 在正常的开发中,文件下载的功能是必不可少,比如我们在论坛看到好看图片好听的歌时,将其下载下来时就…...
【学习笔记】 - GIT的基本操作,IDEA接入GIT以及上传hub
用github蛮多,但git没怎么用,看着视频对着写点笔记以及操作 一、GIT文件的三种状态和模式 已提交(committed) 已提交表示数据已经安全的保存在本地数据库中。 已修改(modified) 已修改表示修改了文件,但还没保存到数据库中。…...

Antd React Form.Item内部是自定义组件怎么自定义返回值
在线演示https://stackblitz.com/edit/stackblitz-starters-xwtwyz?filesrc%2FSelfTreeSelect.tsx 需求 当我们点击提交,需要返回用户名和选中树的id信息,但是,我不关要返回树的id信息,还需要返回选中树的名称 //默认返回的 {userName:梦洁,treeInfo:leaf1-value } //但是需…...
)
2023最新ACL大模型论文分类汇总(有代码的)
1 大模型文化道德 Knowledge of cultural moral norms in large language models url:https://aclanthology.org/2023.acl-long.26/code:https://github.com/AidaRamezani/cultural_inference 2 长文本推理 Open-ended Long Text Generation via Mask…...
Java版 招投标系统简介 招投标系统源码 java招投标系统 招投标系统功能设计
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

Ubuntu 22.04源码安装cmake 3.27.7
安装参考博客是《ubuntu安装cmake》和《Ubuntu 安装CMake》。 https://cmake.org/download是cmake官网下载的网址。 sudo wget -c https://github.com/Kitware/CMake/releases/download/v3.27.7/cmake-3.27.7.tar.gz可以下载源码,最后显示‘cmake-3.27.7.tar.gz’…...
无人地磅称重系统|自助过磅 料仓联动 自助卸料
上海思伟无人地磅系统 自助过磅、 自助卸料 、料仓联动 智能、省人、安全 无人监管过磅 对地磅及其相关的所有硬件进行配置和管理; 支持红外、道闸、车牌识别、AI分析、拍照存档、LED语音播报一体机等设备; 实现稳定可靠的无人监管称重功能…...

冥想第九百七十三天
1.今天周六,很冷的天,上午上了一上午的日语课。 2.下午去看了朋友刚出生的孩子。 3.充实的一天。感谢父母,感谢朋友,感谢家人,感谢不断进步的自己....

ROS 学习应用篇(三)话题Topic学习之自定义话题消息的类型的定义与调用
自定义消息类型的定义 Person.msg文件的定义(数据接口文件的定义) 创建msg文件 首先在功能包下新建msg文件夹,接着在该文件夹下创建文件。 定义msg文件内容 一个消息最重要的就是数据结构类型。这就需要引入一个msg文件,用于…...
财税服务展示预约小程序的作用是什么
财税财政往往困扰着很多公司,尤其是公司里没有相应职员或工作压力大的情况下,不少商家就会寻找代理记账、审计服务、会计代理等服务的机构。 对财政服务代理机构(会计公司)来说,市场企业多而广,理论上来说…...
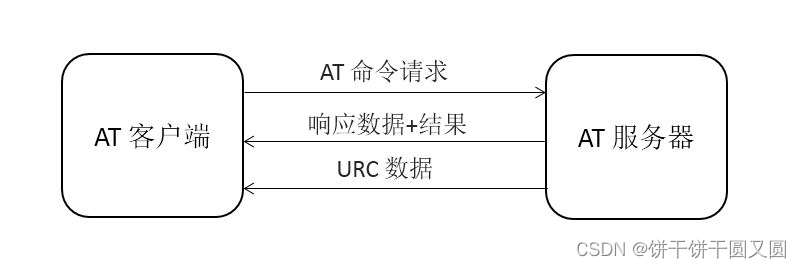
RT-Thread提供的网络世界入口 -net组件
作为一款在RTOS领域对网络支持很丰富的RT-Thread,对设备联网功能的支持的工具就是net组件。 位于/rt-thread/components/net路劲下,作为一款基础组件,env与Studio的工程配置项界面的配置项都依赖该目录下的Kconfig。 我们对网络功能的选择&am…...
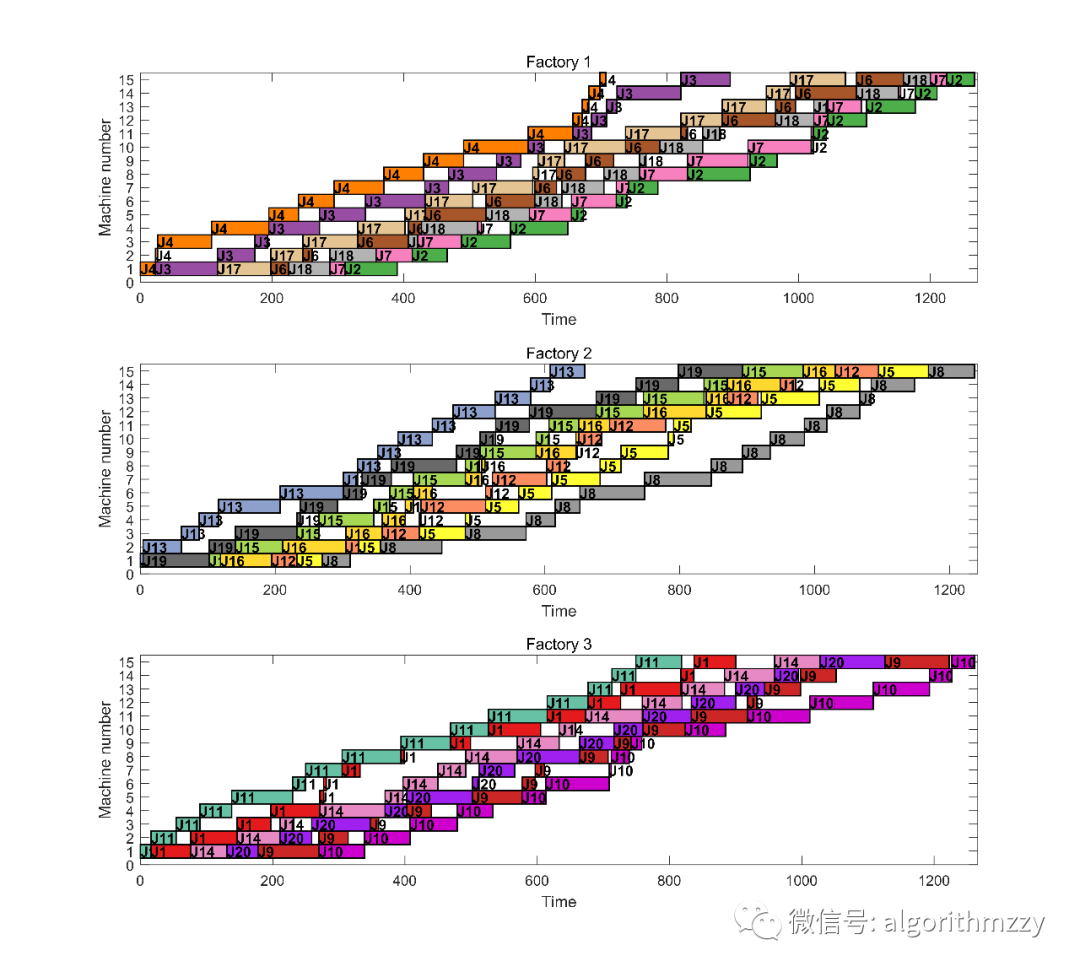
分享一些有趣的MATLAB提示音(代码可直接复制)
先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法,经典的,或者是近几年…...

软件测试|selenium执行js脚本
JavaScript是运行在客户端(浏览器)和服务器端的脚本语言,允许将静态网页转换为交互式网页。可以通过 Python Selenium WebDriver 执行 JavaScript 语句,在Web页面中进行js交互。那么js能做的事,Selenium应该大部分也能…...

【源码复现】图神经网络之PPNP/APPNH
目录 1、论文简介2、论文核心介绍2.1、现有方法局限2.2、PageRank&Personalized PageRank2.3、PPNP&APPNP 3、源码复现3.1、模型总体框架3.2、PPNP3.3、APPNP3.4、MLP(两层) 1、论文简介 论文题目——《PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALI…...
【算法与数据结构】131、LeetCode分割回文串
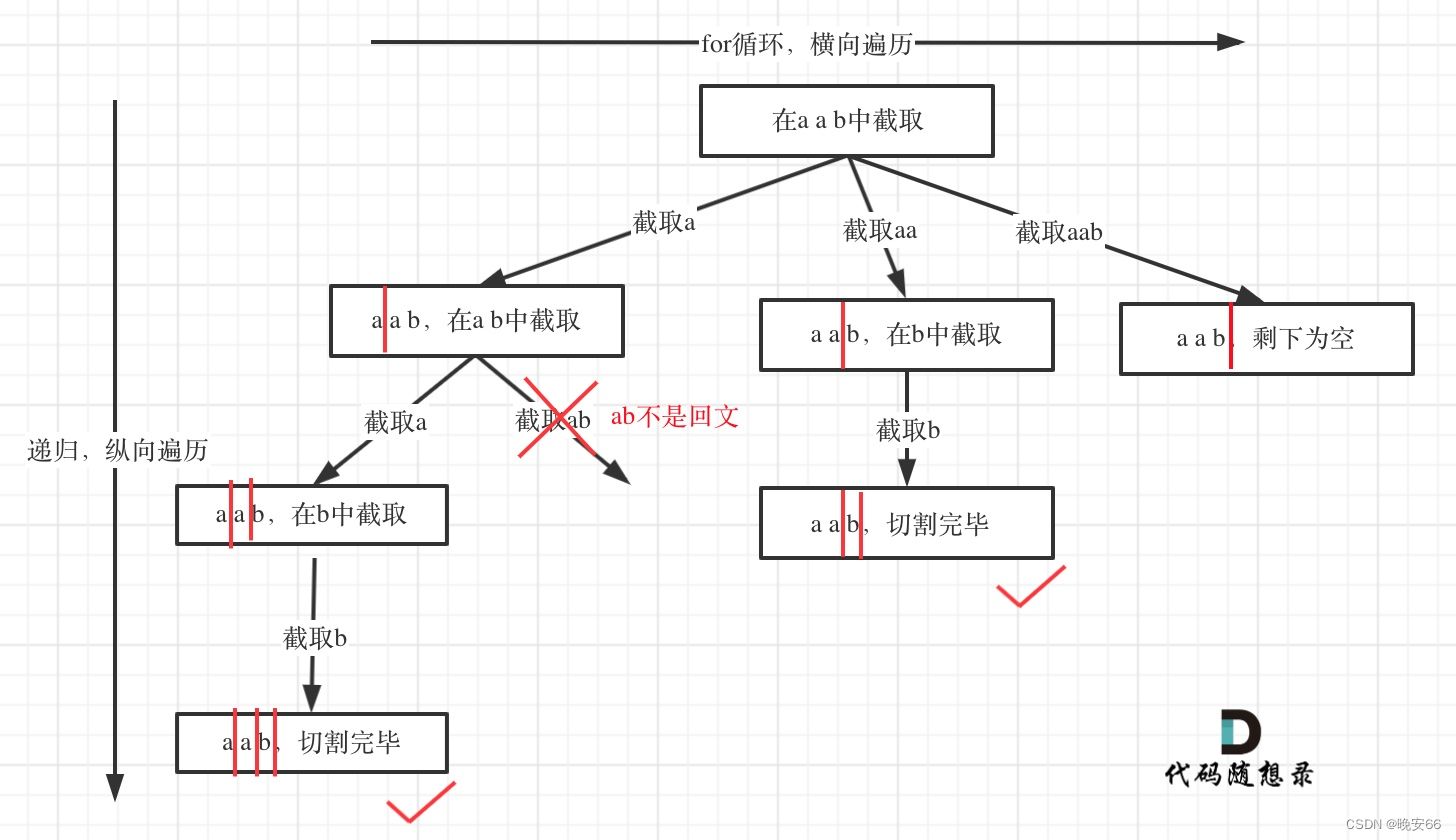
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题仍然使用回溯算法的一般结构。加入了一个判断是否是回文串的函数,利用起始和终止索引进…...

网络编程学习笔记
参考: 套接字通信部分 《TCP/IP 网络编程》以及《TCP/IP网络编程》学习笔记 socket 编程 1. 字节序 字节序,顾名思义字节的顺序,就是大于一个字节类型的数据在内存中的存放顺序,也就是说对于单字符来说是没有字节序问题的&…...
腾讯待办停运后怎么办呢?导出的ics文件怎么打开查看
待办类工具在日常工作中的应用是比较广泛的,很多人会选择使用待办软件记录备忘事项,其中一些提醒类的工具是比较广泛使用的。腾讯待办属于一款待办事项和日程管理工具,它通常是以微信小程序的形式,为大家提供时间管理规划…...

家长群如何发成绩?
老师们是否经常被家长们追问:“老师,我孩子的成绩出来了吗?”、“老师,我孩子考了多少分?”等等。要想解决这个问题,看完这篇文章你就可以让家长们能够自助查询孩子的成绩了。 一、什么是成绩查询系统&…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
