【源码复现】图神经网络之PPNP/APPNH
目录
- 1、论文简介
- 2、论文核心介绍
- 2.1、现有方法局限
- 2.2、PageRank&Personalized PageRank
- 2.3、PPNP&APPNP
- 3、源码复现
- 3.1、模型总体框架
- 3.2、PPNP
- 3.3、APPNP
- 3.4、MLP(两层)
1、论文简介
- 论文题目——《PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK》
- 论文作者——Johannes Klicpera, Aleksandar Bojchevski & Stephan Gu ̈nnemann
- 论文地址——PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK
- 源码——源码链接
2、论文核心介绍
2.1、现有方法局限
现有的方法,仅仅使用了局部有限的邻域信息,更大的邻域信息并没有考虑到。例如,GCN,它采用平均的方法来聚合一阶邻域信息,通过堆叠多层来考虑到更高阶的邻域信息(论文中实际是两层);GAT则是采用注意力机制来学习不同邻域结点信息对当前结点的重要性,也就是说它是对周围邻域结点信息的加权平均。上述方法仍然是浅层的网络,并没有利用到深层邻域信息。
现有方法的另外一个缺点就是过平滑现象(oversmoothing),这也是GCN不能堆叠多层的原因所在。另有作者,通过建立GCN和随机游走(random walk)的关系,发现当GCN的层数增加,GCN会收敛到随机游走的极限分布,会使不同类的结点之间变得不可分,导致GCN性能下降。
为了解决上述的问题,作者提出了一个新的传播方案,这个方案的灵感来自于个性化PageRank算法,它平衡了局部邻域信息与更大的邻域信息的需要,允许更多的传播步骤而不会导致过平滑现象。此外,作者将神经网络从信息传播中分开来,允许去实现更大范围的传播而不用改变神经网络结构,由于这种特性,也可以将SOTA预测方法与文中的传播方案进行融合。
2.2、PageRank&Personalized PageRank
PageRank算法通过网页链接重要性得分计算。重要性可认为是网页链接点击。PageRank算法给定一个概率值,定义为网页访问的概率。一般地, 1 N \frac{1}{N} N1 表示为每个网页节点初始化的概率, P R \rm{PR} PR也是一个初始化的概率值。PageRank 是一个迭代算法,因此 P R \rm{PR} PR 值初始化 1 N \frac{1}{N} N1 , N N N表示为节点的数量。 P R \rm{PR} PR值的总和一般为1,当 P R {\rm{PR}} PR越大,说明重要性越大。
给定节点 v v v,求节点 v v v的 P R {\rm{PR}} PR值,
P R ( v ) = ∑ u ∈ N v P R ( u ) O ( u ) PR(v) = \sum_{u \in \mathcal{N}_v }\frac{PR(u)}{O(u)} PR(v)=u∈Nv∑O(u)PR(u)
N v \mathcal{N}_v Nv表示所有链接到节点 v v v的集合。 O ( u ) O(u) O(u)表示节点 u u u的对外链接数。最早提出的PageRank算法存在着一些缺点,例如当一些节点存在自链接,或者是一些节点的出链节点形成循环圈时,PageRank在迭代过程中会出现 P R {\rm{PR}} PR持续增大,不会减小的情况。对于上述问题,PageRank算法被重新进行改进
P R ( v ) = α ∑ u ∈ N v P R ( u ) O ( u ) + ( 1 − α ) N \mathrm{PR(v)=}\alpha\sum_{\mathrm{u}\in\mathcal{N}_v}\frac{\mathrm{PR(u)}}{\mathrm{O(u)}}+\frac{(1-\alpha)}{\mathrm{N}} PR(v)=αu∈Nv∑O(u)PR(u)+N(1−α)
α \alpha α是一个超参数,取值一般为0.85。 α \alpha α表示节点跳转时的概率,不依据节点之间的链接进行跳转。
PageRank算法衍生出的模型个性化的PageRank算法,主要利用图中节点的链接关系来迭代计算节点的权重。PageRank算法使用随机游走的策略来访问图中节点。PageRank算法与个性化Page Rank算法的区别在于随机游走时的跳转行为不同。个性化的PageRank算法对跳转行为进行约束,指定调转到的对外链接为特定的节点。例如在个性化排序时,用户只能跳转到一些特定的节点,这些节点表示用户偏好的那些节点。
PPR ′ ( v ) = α ∑ u ∈ N v P R ( u ) O ( u ) + ( 1 − α ) r v \text{PPR}^{'}(\mathrm{v})=\alpha\sum_{\mathrm{u}\in\mathcal{N}_v}\frac{\mathrm{PR(u)}}{\mathrm{O(u)}}+(1-\alpha)\mathrm{r}_\mathrm{v} PPR′(v)=αu∈Nv∑O(u)PR(u)+(1−α)rv
r v = { 1 v = u 0 v ≠ u \mathrm r_\mathrm{v}=\begin{cases}1&\mathrm{~v=u}\\0&\mathrm{~v\neq u}\end{cases} rv={10 v=u v=u
个性化PageRank算法中,用户的偏好表示为 r ∣ v ∣ = 1 \mathrm r|\mathrm{v}| = 1 r∣v∣=1,原始的PageRank采用的计算方式为 Π p r = A r w Π p r \Pi_{pr} = A_{rw}\Pi_{pr} Πpr=ArwΠpr, Π p r 是 A r w \Pi_{pr}是A_{rw} Πpr是Arw的特征向量, A r w = A D − 1 A_{rw}=AD^{-1} Arw=AD−1。类似的,个性化的PageRank 算法可以表示为
Π p p r ( i x ) = ( 1 − α ) A ~ Π p p r ( i x ) + α i x \Pi_{\mathrm{ppr}}(\mathbf{i_x})=(1-\alpha)\tilde{{A}}\Pi_{\mathrm{ppr}}(\mathbf{i_x})+\alpha\mathbf{i_x} Πppr(ix)=(1−α)A~Πppr(ix)+αix
参考连接
2.3、PPNP&APPNP
上一节,我们知道了Personalized PageRank算法及其他的表达式,对上式进行求解,求得 Π p p r \Pi_{\mathrm{ppr}} Πppr为
Π p p r ( i x ) = α ( I n − ( 1 − α ) A ~ ) − 1 i x \Pi_{\mathrm{ppr}}(\mathbf{i_{x}})=\alpha(\mathbf{I_n}-(1-\alpha)\tilde{\mathbf{A}})^{-1}\mathbf{i_{x}} Πppr(ix)=α(In−(1−α)A~)−1ix
其中, A ~ = D ~ − 1 2 A ^ D ~ − 1 2 , A ^ = A + I , i x 是传送向量 \tilde{A}=\tilde{D}^{-\frac{1}{2}}\hat{A}\tilde{D}^{-\frac{1}{2}},\hat{A} = A+I,\mathrm{i_x}是传送向量 A~=D~−21A^D~−21,A^=A+I,ix是传送向量。最终的PPNP算法公式表达如下:
Z p p n p = s o f t m a x ( α ( I n − ( 1 − α ) A ~ ) − 1 H ) Z_{\mathrm{ppnp}} = \mathrm{softmax}(\alpha(\mathbf{I_n}-(1-\alpha)\tilde{\mathbf{A}})^{-1}\mathbf{H}) Zppnp=softmax(α(In−(1−α)A~)−1H)
H i , : = f θ ( X i , : ) \mathbf{H}_{i,:} = f_{\theta}(\mathbf{X}_{i,:}) Hi,:=fθ(Xi,:)
其中 X \mathbf{X} X是特征向量矩阵, f θ f_{\theta} fθ是具有参数集合 θ \theta θ的神经网络, H ∈ R n × c \mathbf{H} \in R^{n \times c} H∈Rn×c。
由于在计算上式的时候,需要求矩阵的逆运算,这是一个耗时的操作,为了加速PPNP的训练速度,作者采用一种近似操作来求解,称为APPNP。
Z ( 0 ) = H = f θ ( X ) , Z ( k + 1 ) = ( 1 − α ) A ~ Z ( k ) + α H , Z ( K ) = s o f t m a x ( ( 1 − α ) A ~ Z ( K − 1 ) + α H ) Z^{(0)}=H=f_\theta(\mathbf{X}),\\ Z^{(k+1)} =(1-\alpha)\tilde{A}Z^{(k)}+\alpha H,\\ Z^{(K)}=\mathrm{softmax}((1-\alpha)\tilde{A}Z^{(K-1)}+\alpha H) Z(0)=H=fθ(X),Z(k+1)=(1−α)A~Z(k)+αH,Z(K)=softmax((1−α)A~Z(K−1)+αH)
其中, K K K是迭代次数。作者也在后面的附录中也证明了APPNP当 K ⟶ ∞ K \longrightarrow \infty K⟶∞时,收敛到PPNP,所以APPNP可以看作PPNP的迭代解。
模型的框架如下图所示:

3、源码复现
模型复现源码链接链接:点我点我 提取码:6666
3.1、模型总体框架
import torch
from torch.nn import Module
import torch.nn as nn
from torch.nn import functional as F
import numpy as npclass PPNP(nn.Module):def __init__(self,model,propagation):super(PPNP,self).__init__()self.model = modelself.propagation = propagationdef forward(self,feature,adj):#Generate Prediction#用于生成预测if self.model.__class__.__name__ =='MLP':output = self.model(feature)else:output = self.model(feature,adj)#通过个性化PageRank传播if self.propagation is not None:output = self.propagation(output)#返回最后一层的结果return F.log_softmax(output,dim=1)
3.2、PPNP
class PPNPExtract(Module):def __init__(self,alpha,adj,dropout):super(PPNPExtract,self).__init__()self.alpha = alphaself.adj = adjself.dropout = dropoutpassdef forward(self,H):inv = self.PPR()inv = F.dropout(inv,self.dropout,training=self.training)return self.alpha * torch.mm(inv,H) def PPR(self):if isinstance(self.adj,torch.Tensor):ADJ = self.adj.to_dense().numpy()I_n = np.eye(self.adj.shape[0])M = I_n-(1-self.alpha)*ADJinv_M = np.linalg.inv(M)return torch.Tensor(inv_M)
3.3、APPNP
class PowerIteration(Module):def __init__(self,adj,alpha,k,dropout):super(PowerIteration,self).__init__()self.adj = adjself.alpha = alphaself.k = kself.dropout = dropoutdef forward(self,H):Z = Hfor _ in range(self.k):Z = F.dropout(Z,self.dropout,training=self.training)Z = (1-self.alpha)*torch.mm(self.adj,Z) + self.alpha * Hreturn Z3.4、MLP(两层)
class MLP(Module):def __init__(self,input_dim,hid_dim,output_dim,dropout):super(MLP,self).__init__()self.input_dim = input_dimself.hid_dim = hid_dimself.output_dim = output_dimself.dropout = dropoutself.layer1 = nn.Linear(input_dim,hid_dim,bias=False)self.layer2 = nn.Linear(hid_dim,output_dim,bias=False)def forward(self,X):X = F.dropout(X,self.dropout,training=self.training)X = self.layer1(X)X = F.relu(X)X = F.dropout(X,self.dropout,training=self.training)X = self.layer2(X)return Xdef __repr__(self) -> str:return self.__class__.__name__
相关文章:

【源码复现】图神经网络之PPNP/APPNH
目录 1、论文简介2、论文核心介绍2.1、现有方法局限2.2、PageRank&Personalized PageRank2.3、PPNP&APPNP 3、源码复现3.1、模型总体框架3.2、PPNP3.3、APPNP3.4、MLP(两层) 1、论文简介 论文题目——《PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALI…...
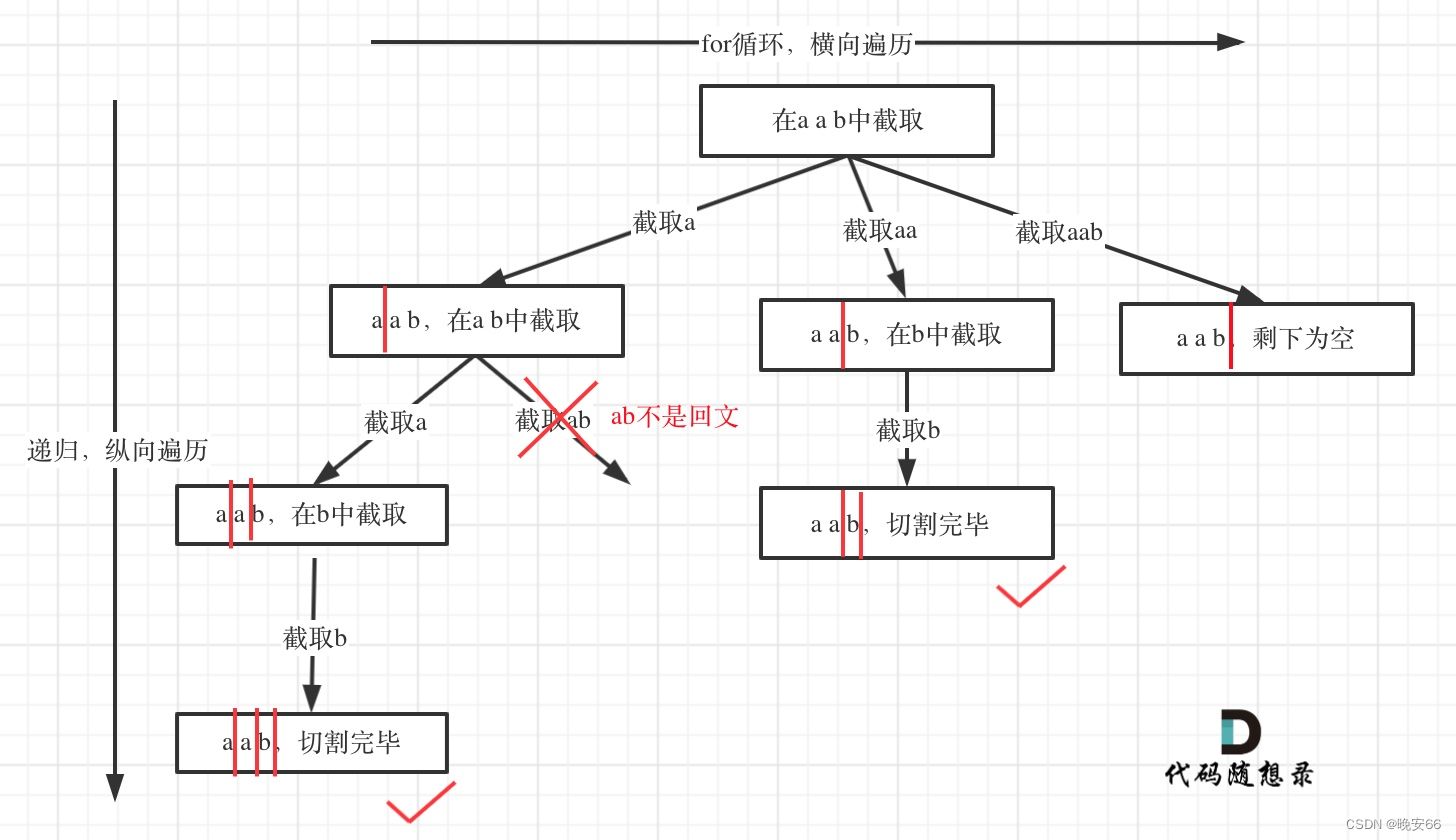
【算法与数据结构】131、LeetCode分割回文串
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题仍然使用回溯算法的一般结构。加入了一个判断是否是回文串的函数,利用起始和终止索引进…...

网络编程学习笔记
参考: 套接字通信部分 《TCP/IP 网络编程》以及《TCP/IP网络编程》学习笔记 socket 编程 1. 字节序 字节序,顾名思义字节的顺序,就是大于一个字节类型的数据在内存中的存放顺序,也就是说对于单字符来说是没有字节序问题的&…...
腾讯待办停运后怎么办呢?导出的ics文件怎么打开查看
待办类工具在日常工作中的应用是比较广泛的,很多人会选择使用待办软件记录备忘事项,其中一些提醒类的工具是比较广泛使用的。腾讯待办属于一款待办事项和日程管理工具,它通常是以微信小程序的形式,为大家提供时间管理规划…...

家长群如何发成绩?
老师们是否经常被家长们追问:“老师,我孩子的成绩出来了吗?”、“老师,我孩子考了多少分?”等等。要想解决这个问题,看完这篇文章你就可以让家长们能够自助查询孩子的成绩了。 一、什么是成绩查询系统&…...
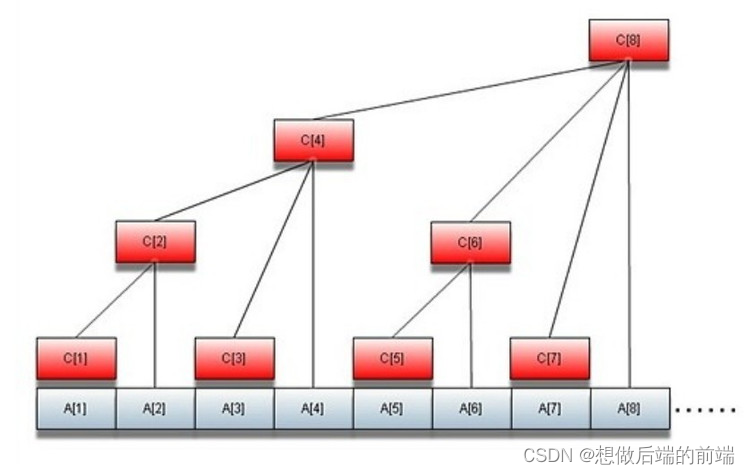
数组区域检索的优化 --- 分块,线段树,树状数组
思考 首先让我们来思考一个问题,给定一个数组,和left与right的值,让你求这个数组中left到right之间元素的和,你会怎么计算?最简单的当然是遍历。如果有人问你这个问题的时候,他决对是会让你优化的ÿ…...
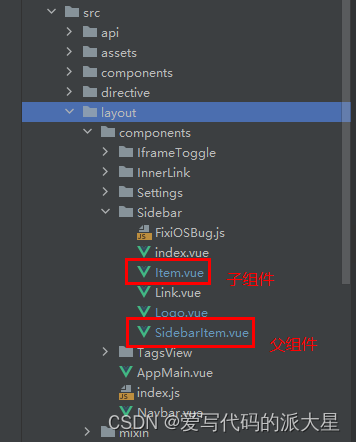
若依侧边栏添加计数标记效果
2023.11.13今天我学习了如何对若依的侧边栏添加技术标记的效果,如图: 我们需要用到两个页面: 先说子组件实现计数标记效果 1.item.vue <script> export default {name: MenuItem,functional: true,props: {icon: {type: String,defau…...

WebSocket技术解析:实现Web实时双向通信的利器
当今互联网的发展中,实时性成为了越来越重要的需求,特别是在Web应用程序中。传统的HTTP协议在处理实时性方面存在一些局限性,因此WebSocket技术的出现填补了这一空白。WebSocket是一种在单个TCP连接上进行全双工通信的协议,它允许…...

深圳联强优创手持PDA身份证阅读器 身份证核验手持机
身份证手持机外观比较小巧,方便携带,支持条码识别、人脸识别、NFC卡刷卡、内置二代证加密模块,可离线采集和识别二代身份证,进行身份识别。信息读取更便捷、安全高效。采用IP65高防护等级,1.5M防摔,可以适应…...

力扣labuladong——一刷day31
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣226. 翻转二叉树二、力扣116. 填充每个节点的下一个右侧节点指针三、力扣114. 二叉树展开为链表 二叉树解题的思维模式分两类: 1、是否可以…...
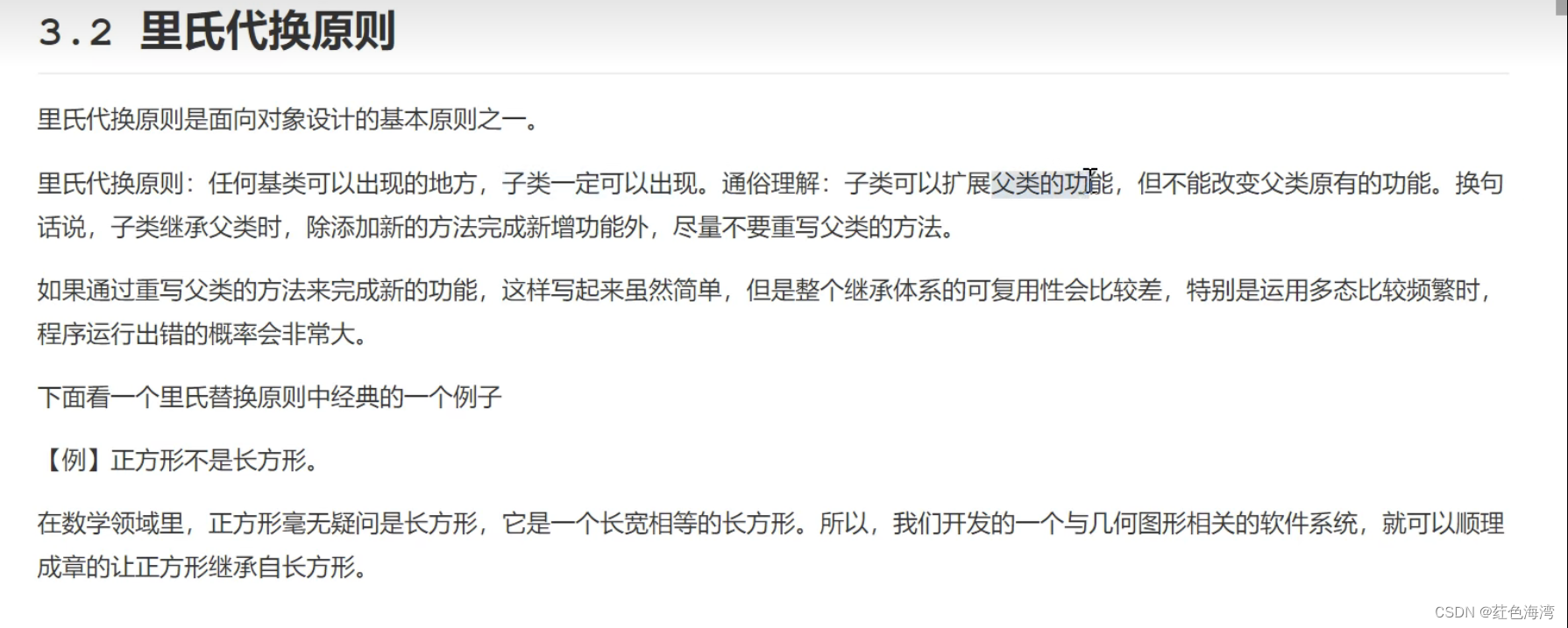
里氏代换原则
package com.jmj.principles.dmeo2.after;/*** 四边形接口*/ public interface Quadrilateral {double getLength();double getWidth();}package com.jmj.principles.dmeo2.after;/*** 长方形类*/ public class Rectangle implements Quadrilateral{private double length;priv…...
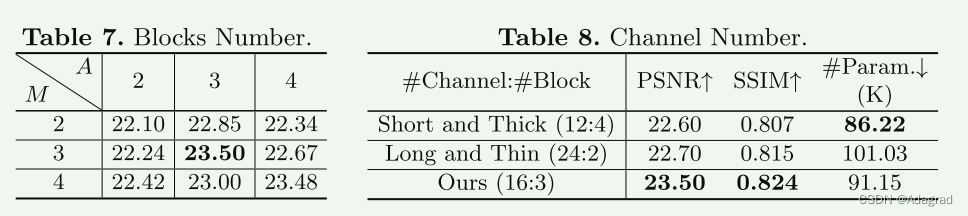
Illumination Adaptive Transformer
Abstract. 现实世界中具有挑战性的照明条件(低光、曝光不足和曝光过度)不仅会产生令人不快的视觉外观,还会影响计算机视觉任务。现有的光自适应方法通常单独处理每种情况。更重要的是,它们中的大多数经常在 RAW 图像上运行或过度…...

【教3妹学编程-算法题】给小朋友们分糖果 II
3妹:1 8得8,2 816, 3 8妇女节… 2哥 : 3妹,在干嘛呢 3妹:双11不是过了嘛, 我看看我这个双十一买了多少钱, 省了多少钱。 2哥 : 我可是一分钱没买。 3妹:我买了不少东西, …...
应急响应练习2
目录 1. 请提交攻击者的ip与系统版本 2. 攻击者通过某个组件漏洞获得服务器权限,请提交该组件的名称 3. 请提交攻击者首次攻击成功的时间 4. 请提交攻击者上传的webshell文件绝对路径 5. 请提交攻击者使用的webshell管理工具 6. 攻击者进一步留下的免杀的webs…...

JS算法练习 11.13
leetcode 2625 扁平化嵌套数组 请你编写一个函数,它接收一个 多维数组 arr 和它的深度 n ,并返回该数组的 扁平化 后的结果。 多维数组 是一种包含整数或其他 多维数组 的递归数据结构。 数组 扁平化 是对数组的一种操作,定义是将原数组部…...

js升序排序
function sortByKey(array, key) {return array.sort(function(a, b) {var x Number(a[key]);var y Number(b[key]);return x < y ? -1 : x > y ? 1 : 0; //或者 return x-y});}...

2023亚太杯数学建模C题思路
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

【ArcGIS Pro微课1000例】0030:ArcGIS Pro中自带晕渲地貌工具的妙用
在ArcGIS中,制作地貌晕渲效果通常的做法是先制作山体阴影效果,然后叠加在DEM的下面,再改变DEM的透明度来实现。而在ArcGIS Pro中自带了效果显著的晕渲地貌工具。 文章目录 一、晕渲地貌工具1. 符号系统2. 栅格函数二、山体阴影效果1. 工具箱2. 栅格函数打开ArcGIS Pro3.0,加…...
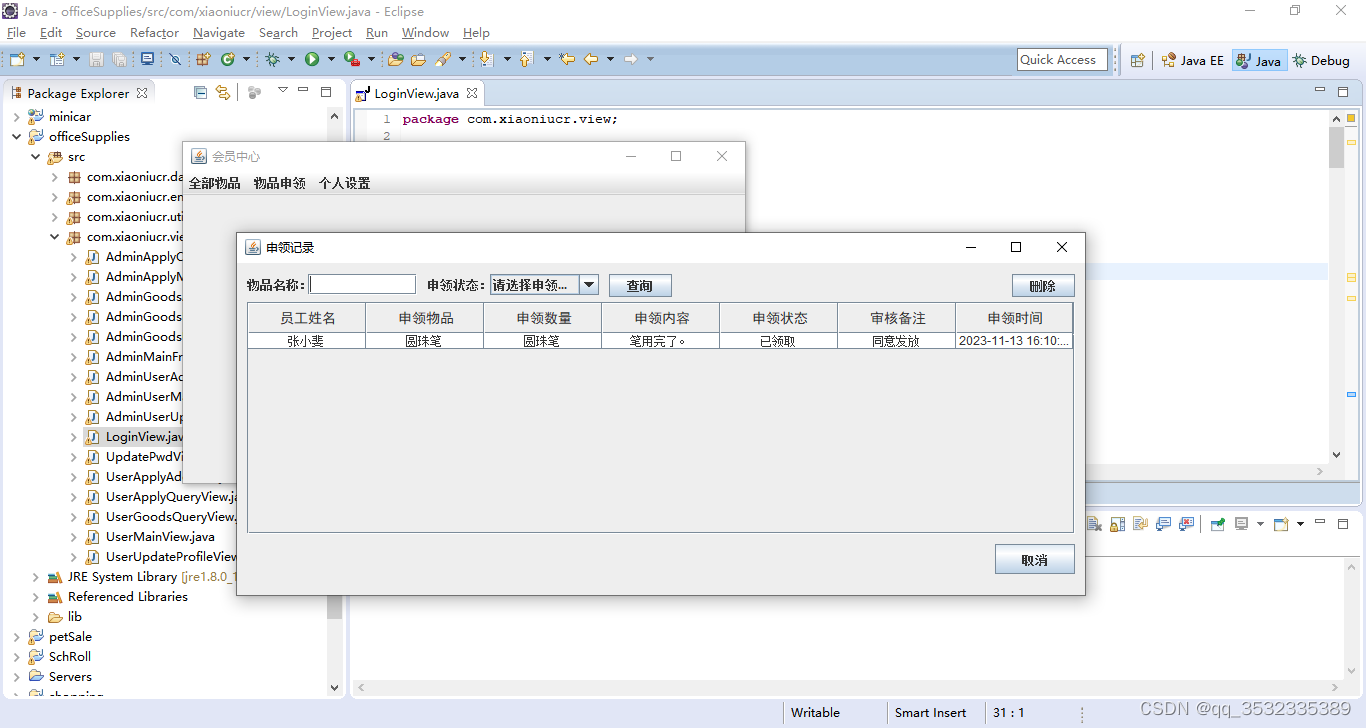
【原创】java+swing+mysql办公用品管理系统设计与实现
摘要: 办公用品管理系统是一个设计和实现办公用品库存和使用管理的信息系统。此系统可以提高办公用品的利用率,减少浪费,使办公用品管理更加高效、规范、便捷。本文主要介绍使用javaswingmysql技术去开发实现一个办公用品管理系统。 功能分…...

sqlalchemy查询数据为空,查询范围对应的数据在数据库真实存在
记录一个开发过程遇到的小bug,构造些伪数据还原并解释。 """ 场景:传参触发了查询条件,数据库中是存在传参对应范围的数据,但是通过查询条件得到的查询结果为空 """ 入参场景一: start_time = "2023-11-13" end_time = "202…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
