力扣labuladong——一刷day31
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、力扣226. 翻转二叉树
- 二、力扣116. 填充每个节点的下一个右侧节点指针
- 三、力扣114. 二叉树展开为链表
二叉树解题的思维模式分两类: 1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。 2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。 无论使用哪种思维模式,你都需要思考: 如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
前言
一、力扣226. 翻转二叉树
遍历思想
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {treaverse(root);return root;}public void treaverse(TreeNode root){if(root == null){return;}TreeNode l = root.left;root.left = root.right;root.right = l;treaverse(root.left);treaverse(root.right);}
}
分解思想
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {return fun(root);}public TreeNode fun(TreeNode root){if(root == null){return null;}TreeNode lchild = fun(root.left);TreeNode rchild = fun(root.right);root.left = rchild;root.right = lchild;return root;}
}
二、力扣116. 填充每个节点的下一个右侧节点指针
/*
// Definition for a Node.
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
*/class Solution {public Node connect(Node root) {if(root == null){return root;}if(root.left != null && root.right != null){fun(root.left, root.right);}return root;}public void fun(Node node1, Node node2){if(node1 == null || node2 == null){return ;}node1.next = node2;fun(node1.left, node1.right);fun(node2.left,node2.right);fun(node1.right,node2.left);}
}
三、力扣114. 二叉树展开为链表
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public void flatten(TreeNode root) {fun(root);}public TreeNode fun(TreeNode root){if(root == null){return null;}TreeNode r1 = fun(root.left);TreeNode r2 = fun(root.right);if(r1 != null && r2 != null){r1.right = root.right;root.right = root.left;root.left = null;return r2;}if(r1 == null && r2 != null){return r2;}if(r2 == null && r1 != null){root.right = root.left;root.left = null;return r1;}return root;}
}
第二种解法
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public void flatten(TreeNode root) {if(root == null){return;}TreeNode r1 = root.left;TreeNode r2 = root.right;flatten(root.left);flatten(root.right);root.left = null;root.right = r1;TreeNode p = root;while(p.right != null){p = p.right;}p.right = r2;}
}
相关文章:

力扣labuladong——一刷day31
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣226. 翻转二叉树二、力扣116. 填充每个节点的下一个右侧节点指针三、力扣114. 二叉树展开为链表 二叉树解题的思维模式分两类: 1、是否可以…...
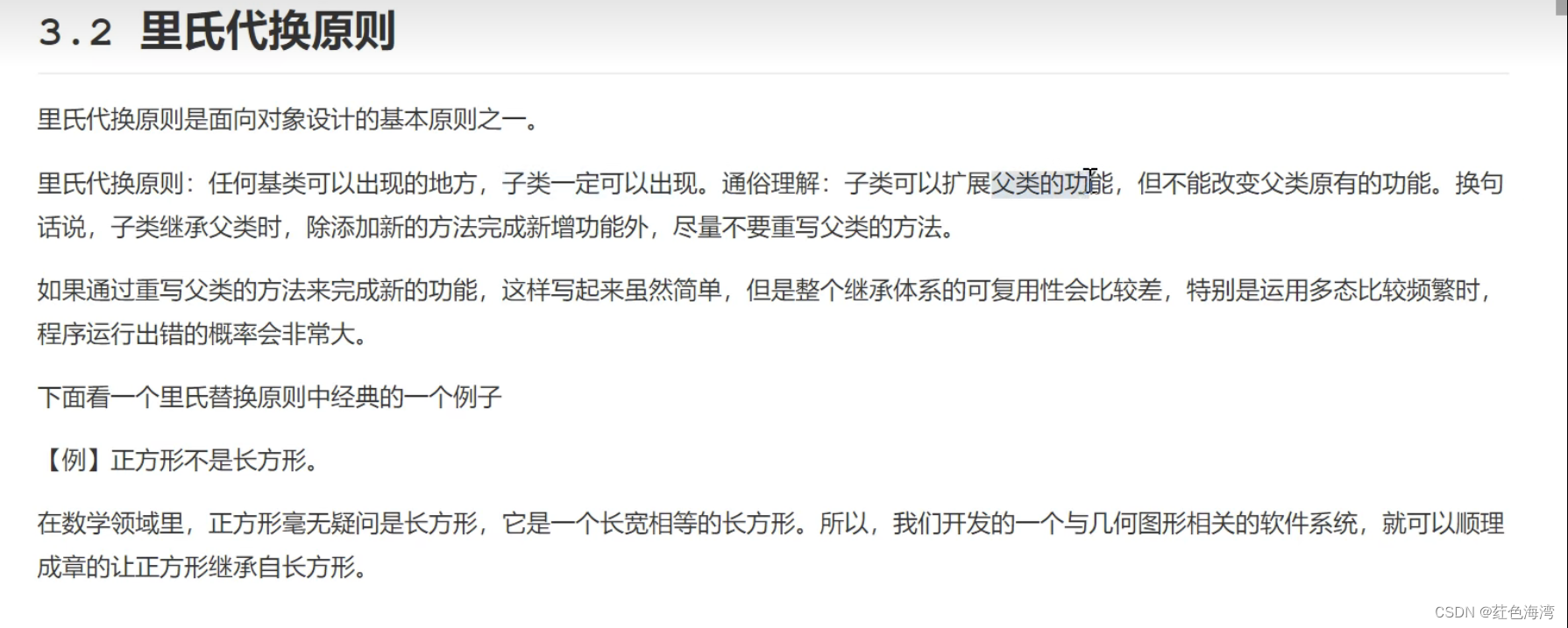
里氏代换原则
package com.jmj.principles.dmeo2.after;/*** 四边形接口*/ public interface Quadrilateral {double getLength();double getWidth();}package com.jmj.principles.dmeo2.after;/*** 长方形类*/ public class Rectangle implements Quadrilateral{private double length;priv…...
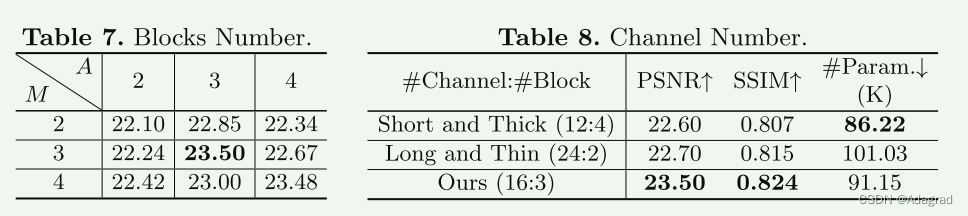
Illumination Adaptive Transformer
Abstract. 现实世界中具有挑战性的照明条件(低光、曝光不足和曝光过度)不仅会产生令人不快的视觉外观,还会影响计算机视觉任务。现有的光自适应方法通常单独处理每种情况。更重要的是,它们中的大多数经常在 RAW 图像上运行或过度…...

【教3妹学编程-算法题】给小朋友们分糖果 II
3妹:1 8得8,2 816, 3 8妇女节… 2哥 : 3妹,在干嘛呢 3妹:双11不是过了嘛, 我看看我这个双十一买了多少钱, 省了多少钱。 2哥 : 我可是一分钱没买。 3妹:我买了不少东西, …...
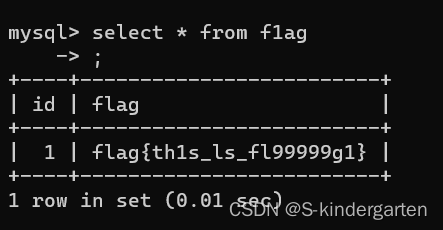
应急响应练习2
目录 1. 请提交攻击者的ip与系统版本 2. 攻击者通过某个组件漏洞获得服务器权限,请提交该组件的名称 3. 请提交攻击者首次攻击成功的时间 4. 请提交攻击者上传的webshell文件绝对路径 5. 请提交攻击者使用的webshell管理工具 6. 攻击者进一步留下的免杀的webs…...

JS算法练习 11.13
leetcode 2625 扁平化嵌套数组 请你编写一个函数,它接收一个 多维数组 arr 和它的深度 n ,并返回该数组的 扁平化 后的结果。 多维数组 是一种包含整数或其他 多维数组 的递归数据结构。 数组 扁平化 是对数组的一种操作,定义是将原数组部…...

js升序排序
function sortByKey(array, key) {return array.sort(function(a, b) {var x Number(a[key]);var y Number(b[key]);return x < y ? -1 : x > y ? 1 : 0; //或者 return x-y});}...

2023亚太杯数学建模C题思路
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

【ArcGIS Pro微课1000例】0030:ArcGIS Pro中自带晕渲地貌工具的妙用
在ArcGIS中,制作地貌晕渲效果通常的做法是先制作山体阴影效果,然后叠加在DEM的下面,再改变DEM的透明度来实现。而在ArcGIS Pro中自带了效果显著的晕渲地貌工具。 文章目录 一、晕渲地貌工具1. 符号系统2. 栅格函数二、山体阴影效果1. 工具箱2. 栅格函数打开ArcGIS Pro3.0,加…...
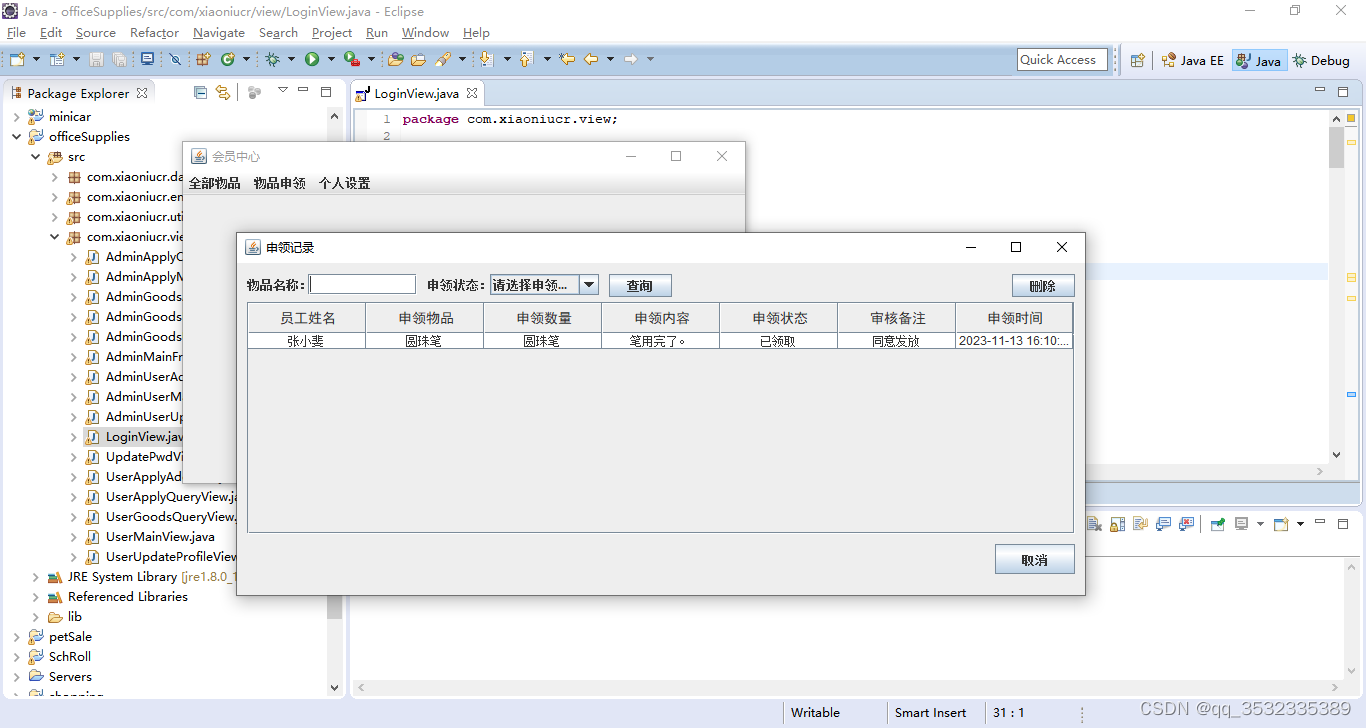
【原创】java+swing+mysql办公用品管理系统设计与实现
摘要: 办公用品管理系统是一个设计和实现办公用品库存和使用管理的信息系统。此系统可以提高办公用品的利用率,减少浪费,使办公用品管理更加高效、规范、便捷。本文主要介绍使用javaswingmysql技术去开发实现一个办公用品管理系统。 功能分…...

sqlalchemy查询数据为空,查询范围对应的数据在数据库真实存在
记录一个开发过程遇到的小bug,构造些伪数据还原并解释。 """ 场景:传参触发了查询条件,数据库中是存在传参对应范围的数据,但是通过查询条件得到的查询结果为空 """ 入参场景一: start_time = "2023-11-13" end_time = "202…...

Code Former安装及使用
Code Former是南洋理工大学和商汤科技联合研究中心联合开发一款AI人脸修复算法,通过该算法,可以对已经模糊的图片进行人脸修复,找回斑驳的记忆 由于网上对于Code Former的封装,全都是要花钱,或者需要其他什么曲折的方式…...

SpringMVC--@RequestMapping注解
RequestMapping注解 RequestMapping注解的功能RequestMapping注解的位置RequestMapping注解的属性1、value属性2、method属性3、params属性(了解) 补充RequestParamRequestHeaderRequestBody RequestBody获取json格式的请求参数 ResponseBodyRestControl…...
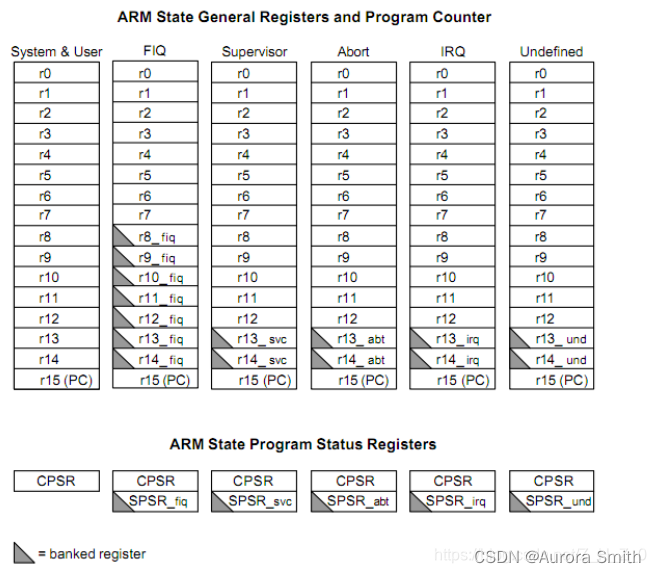
ARM寄存器及功能介绍/R0-R15寄存器
1、ARM 寄存器组介绍 ARM 处理器一般共有 37 个寄存器,其中包括: (1) 31 个通用寄存器,包括 PC(程序计数器)在内,都是 32 位的寄存器。 (2) 6 个状态寄存器…...
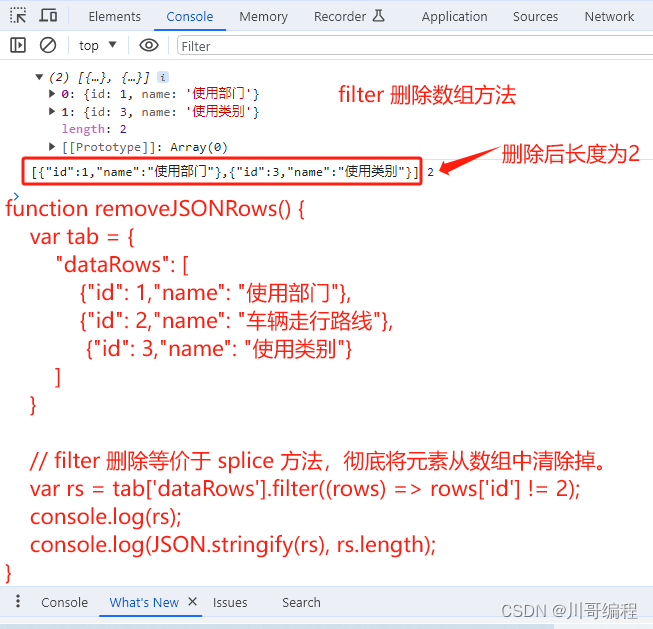
js删除json数据中指定元素
delete 删除数组方法: function removeJSONRows() {var tab {"dataRows": [{"id": 1,"name": "使用部门"},{"id": 2,"name": "车辆走行路线"},{"id": 3,"name": &quo…...

广州华锐互动:VR刑侦现场执法实训助力警察全面提升警务能力
随着科技的不断发展,虚拟现实(VR)技术在多个领域开始得到广泛应用,其中包括公安执法培训。VR刑侦现场执法实训系统是一种采用虚拟现实技术,为公安执法人员提供模拟真实环境的培训工具。通过这种平台,公安人…...
应用程序)
多线程 浏览器渲染引擎 图形用户界面(GUI,Graphical User Interface)应用程序
目录 多线程浏览器渲染引擎图形用户界面(GUI,Graphical User Interface)应用程序 👍 点赞,你的认可是我创作的动力! ⭐️ 收藏,你的青睐是我努力的方向! ✏️ 评论,你的…...
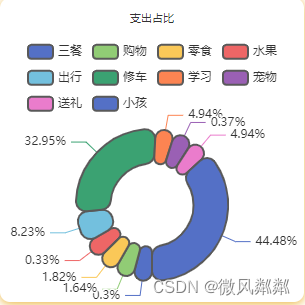
echarts饼图label显示不全原因?
echarts饼图label显示不全原因? 标签数量过多:当饼图的扇形数量较多时,为了保证图形的清晰性,ECharts 可能不会显示所有的标签,而是选择显示部分标签或者不显示标签。标签过长:如果标签的文字过长…...

暖手宝上架亚马逊美国站UL499报告测试标准要求
暖手宝是运用物理及化学原理研制的自动取暖保健用品。该产品以其自动生热,有趣,实用等新颖独特的优势,深受欢迎——暖手宝具有自动取暖,理疗保健等多种功能。只要插上电源等上10分钟左右就能发热,最后一种是通过锂电池…...
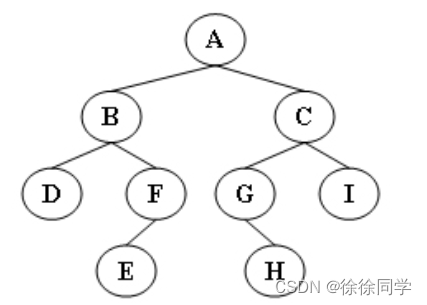
2023数据结构期中测验-2023秋-计算机+未来网络专业
这里写目录标题 选择题函数题6-1 求链式表的表长6-2 逆序数据建立链表6-3 删除单链表偶数节点6-4 求二叉树高度6-5 先序输出叶结点 选择题 2-1 下述程序段的时间复杂度为( ) for(i0; i<n-1; i)for(j0; j<n-1-i…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
