数组区域检索的优化 --- 分块,线段树,树状数组
思考
首先让我们来思考一个问题,给定一个数组,和left与right的值,让你求这个数组中left到right之间元素的和,你会怎么计算?最简单的当然是遍历。如果有人问你这个问题的时候,他决对是会让你优化的,起码时间复杂度一定要小于O(n),那你打算怎么做呢?
很明确的一点是,如果要优化时间复杂度,就必须要提高空间复杂度,这是算法的局限,当然也是自然界的能量守恒定律。这是不可避免的,
所以接下来你可以思考下,有什么结构可以实现了。
分块处理
这种就真的很基础了,就是开辟一个额外的数组来存储区间和。
设数组大小为 n,我们将数组 nums分成多个块,每个块大小 size,最后一个块的大小为剩余的不超过 size 的元素数目,那么块的总数为 n/size,用一个数组 sum 保存每个块的元素和。
那么究竟要分成多少个数组,才能在数量和速度上都是最优解那? 这个关键在于size的取值。在求和时:设left位于b1个块内的第i1个元素,right位于b2个块内的第i2个元素。如果b1=b2,那么直接返回第b1个块位于区间[i1,i2]的元素的和;否则计算第b1个块位于区间[i,size)的元素之和sum1,第b2个块位于区间[0,i2]的元素之和sum2,第b1+1个块到第b2-1个块的元素的总和sum3,返回sum1+sum2+sum3。这个求和的时间复杂度为。因为
,当且仅当
时等号成立。因此size的取值为
。此时的时间复杂度为
var NumArray = function(nums) {this.nums = nums;const n = nums.length;size = Math.floor(Math.sqrt(n));this.sum = new Array(Math.floor((n + size - 1) / size)).fill(0); // n/size 向上取整for (let i = 0; i < n; i++) {this.sum[Math.floor(i / size)] += nums[i];}
};NumArray.prototype.update = function(index, val) {this.sum[Math.floor(index / size)] += val - this.nums[index];this.nums[index] = val;
};NumArray.prototype.sumRange = function(left, right) {const b1 = Math.floor(left / size), i1 = left % size, b2 = Math.floor(right / size), i2 = right % size;if (b1 === b2) { // 区间 [left, right] 在同一块中let sum = 0;for (let j = i1; j <= i2; j++) {sum += this.nums[b1 * size + j];}return sum;}let sum1 = 0;for (let j = i1; j < size; j++) {sum1 += this.nums[b1 * size + j];}let sum2 = 0;for (let j = 0; j <= i2; j++) {sum2 += this.nums[b2 * size + j];}let sum3 = 0;for (let j = b1 + 1; j < b2; j++) {sum3 += this.sum[j];}return sum1 + sum2 + sum3;
};
线段树
线段树是一种二叉树,也就是对于一个线段,我们会用一个二叉树来表示。比如说一个长度为4的线段,我们可以表示成这样:

这是什么意思呢? 如果你要表示线段的和,那么最上面的根节点的权值表示的是这个线段 1 ∼ 4 的和。根的两个儿子分别表示这个线段中 1 ∼ 2 的和,与 3 ∼ 4 的和。以此类推。
然后我们还可以的到一个性质:节点 i 的权值 = 她的左儿子权值 + 她的右儿子权值。因为 1 ∼ 4 的和就是等于 1 ∼ 2 的和与 2 ∼ 3 的和的和。
给定区间 [left,right]时,我们将区间 [left,right] 拆成多个结点对应的区间。
- 如果结点 node 对应的区间与 [left,right] 相同,可以直接返回该结点的值,即当前区间和。
- 如果结点 node 对应的区间与 [left,right]不同,设左子结点对应的区间的右端点为 m,那么将区间 [left,right] 沿点 m拆成两个区间,分别计算左子结点和右子结点。
我们从根结点开始递归地拆分区间 [left,right]。
var NumArray = function(nums) {n = nums.length;this.segmentTree = new Array(nums.length * 4).fill(0);this.build(0, 0, n - 1, nums);
};NumArray.prototype.update = function(index, val) {this.change(index, val, 0, 0, n - 1);
};NumArray.prototype.sumRange = function(left, right) {return this.range(left, right, 0, 0, n - 1);
};NumArray.prototype.build = function(node, s, e, nums) {if (s === e) {this.segmentTree[node] = nums[s];return;}const m = s + Math.floor((e - s) / 2);this.build(node * 2 + 1, s, m, nums);this.build(node * 2 + 2, m + 1, e, nums);this.segmentTree[node] = this.segmentTree[node * 2 + 1] + this.segmentTree[node * 2 + 2];
}NumArray.prototype.change = function(index, val, node, s, e) {if (s === e) {this.segmentTree[node] = val;return;}const m = s + Math.floor((e - s) / 2);if (index <= m) {this.change(index, val, node * 2 + 1, s, m);} else {this.change(index, val, node * 2 + 2, m + 1, e);}this.segmentTree[node] = this.segmentTree[node * 2 + 1] + this.segmentTree[node * 2 + 2];
}NumArray.prototype.range = function(left, right, node, s, e) {if (left === s && right === e) {return this.segmentTree[node];}const m = s + Math.floor((e - s) / 2);if (right <= m) {return this.range(left, right, node * 2 + 1, s, m);} else if (left > m) {return this.range(left, right, node * 2 + 2, m + 1, e);} else {return this.range(left, m, node * 2 + 1, s, m) + this.range(m + 1, right, node * 2 + 2, m + 1, e);}
}树状数组
树状数组是一种可以动态维护序列前缀和的数据结构(序列下标从 1 开始)
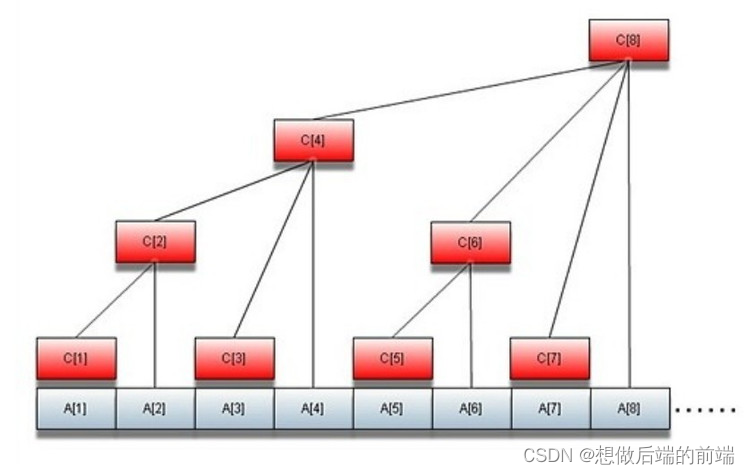
如图,A是基本数组,C是求和数组,
其中,C[1]=A[1], C[2]=C[1]+A[2], C[3]=A[3], C[4]=C[2]+C[3]+A[4]......C[8]=C[4]+C[6]+C[7]+A[8]......
树状数组最简单最经典的使用场景,就是单点更新区间查询:
- 单点修改 add(index,val):把序列第 index 个数增加 val;
- 区间查询 prefixSum(index):查询前 index个元素的前缀和。
前置知识—lowbit(x)运算
如何计算一个非负整数n在二进制下的最低为1及其后面的0构成的数?
例如:44 的二进制表示为 (101100),最低为1和后面的0构成的数是( 100 ) 是 4 。44的二进制=(101100),我们对44的二进制数取反+1,也即~44+1,得到-44
-44的二进制=(010100),然后我们把44和-44的二进制进行按位与运算,也即按位&得到,二进制000100,也就是十进制的4
所以lowbit(x) = x&(-x)
var NumArray = function(nums) {this.tree = new Array(nums.length + 1).fill(0);this.nums = nums;for (let i = 0; i < nums.length; i++) {this.add(i + 1, nums[i]);}
};NumArray.prototype.update = function(index, val) {this.add(index + 1, val - this.nums[index]);this.nums[index] = val;
};NumArray.prototype.sumRange = function(left, right) {return this.prefixSum(right + 1) - this.prefixSum(left);
};NumArray.prototype.lowBit = function(x) {return x & -x;
}NumArray.prototype.add = function(index, val) {while (index < this.tree.length) {this.tree[index] += val;index += this.lowBit(index);}
}NumArray.prototype.prefixSum = function(index) {let sum = 0;while (index > 0) {sum += this.tree[index];index -= this.lowBit(index);}return sum;
}
树状数组和线段树的区别在哪
有人会问了既然线段树的问题能够用树状数组解决而且线段树还比树状数组扩展性强,那为什么不直接用线段树呢?问的很好,树状数组的作用就是为了简化线段树,举个例子:一个问题可以用线段树解决写代码半个小时,但是用树状数组只需要10分钟,那么你会选择哪一个算法呢?没错,基于某些简单的问题,我们没必要用到功能性强但实现复杂的线段树(杀鸡焉用宰牛刀)。当并不是所有能用线段树解决的问题,用树状数组都可以解决。
相关文章:

数组区域检索的优化 --- 分块,线段树,树状数组
思考 首先让我们来思考一个问题,给定一个数组,和left与right的值,让你求这个数组中left到right之间元素的和,你会怎么计算?最简单的当然是遍历。如果有人问你这个问题的时候,他决对是会让你优化的ÿ…...
若依侧边栏添加计数标记效果
2023.11.13今天我学习了如何对若依的侧边栏添加技术标记的效果,如图: 我们需要用到两个页面: 先说子组件实现计数标记效果 1.item.vue <script> export default {name: MenuItem,functional: true,props: {icon: {type: String,defau…...

WebSocket技术解析:实现Web实时双向通信的利器
当今互联网的发展中,实时性成为了越来越重要的需求,特别是在Web应用程序中。传统的HTTP协议在处理实时性方面存在一些局限性,因此WebSocket技术的出现填补了这一空白。WebSocket是一种在单个TCP连接上进行全双工通信的协议,它允许…...

深圳联强优创手持PDA身份证阅读器 身份证核验手持机
身份证手持机外观比较小巧,方便携带,支持条码识别、人脸识别、NFC卡刷卡、内置二代证加密模块,可离线采集和识别二代身份证,进行身份识别。信息读取更便捷、安全高效。采用IP65高防护等级,1.5M防摔,可以适应…...

力扣labuladong——一刷day31
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣226. 翻转二叉树二、力扣116. 填充每个节点的下一个右侧节点指针三、力扣114. 二叉树展开为链表 二叉树解题的思维模式分两类: 1、是否可以…...
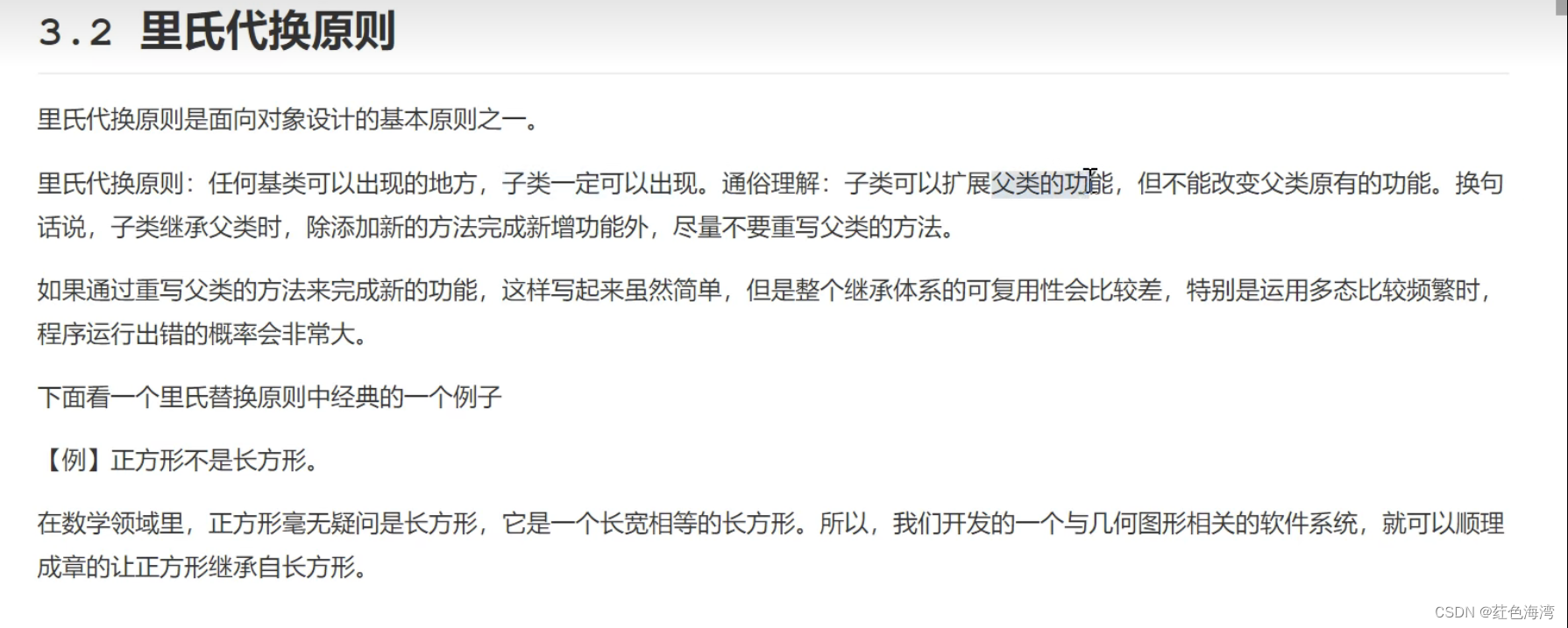
里氏代换原则
package com.jmj.principles.dmeo2.after;/*** 四边形接口*/ public interface Quadrilateral {double getLength();double getWidth();}package com.jmj.principles.dmeo2.after;/*** 长方形类*/ public class Rectangle implements Quadrilateral{private double length;priv…...
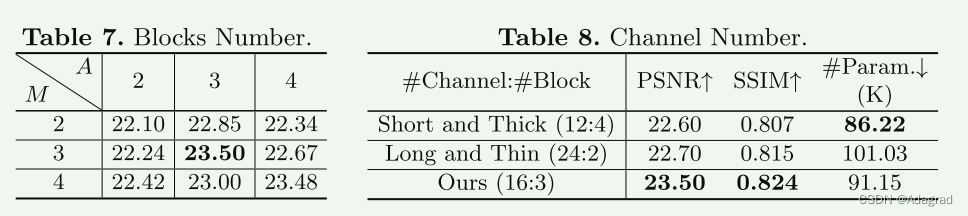
Illumination Adaptive Transformer
Abstract. 现实世界中具有挑战性的照明条件(低光、曝光不足和曝光过度)不仅会产生令人不快的视觉外观,还会影响计算机视觉任务。现有的光自适应方法通常单独处理每种情况。更重要的是,它们中的大多数经常在 RAW 图像上运行或过度…...

【教3妹学编程-算法题】给小朋友们分糖果 II
3妹:1 8得8,2 816, 3 8妇女节… 2哥 : 3妹,在干嘛呢 3妹:双11不是过了嘛, 我看看我这个双十一买了多少钱, 省了多少钱。 2哥 : 我可是一分钱没买。 3妹:我买了不少东西, …...
应急响应练习2
目录 1. 请提交攻击者的ip与系统版本 2. 攻击者通过某个组件漏洞获得服务器权限,请提交该组件的名称 3. 请提交攻击者首次攻击成功的时间 4. 请提交攻击者上传的webshell文件绝对路径 5. 请提交攻击者使用的webshell管理工具 6. 攻击者进一步留下的免杀的webs…...

JS算法练习 11.13
leetcode 2625 扁平化嵌套数组 请你编写一个函数,它接收一个 多维数组 arr 和它的深度 n ,并返回该数组的 扁平化 后的结果。 多维数组 是一种包含整数或其他 多维数组 的递归数据结构。 数组 扁平化 是对数组的一种操作,定义是将原数组部…...

js升序排序
function sortByKey(array, key) {return array.sort(function(a, b) {var x Number(a[key]);var y Number(b[key]);return x < y ? -1 : x > y ? 1 : 0; //或者 return x-y});}...

2023亚太杯数学建模C题思路
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

【ArcGIS Pro微课1000例】0030:ArcGIS Pro中自带晕渲地貌工具的妙用
在ArcGIS中,制作地貌晕渲效果通常的做法是先制作山体阴影效果,然后叠加在DEM的下面,再改变DEM的透明度来实现。而在ArcGIS Pro中自带了效果显著的晕渲地貌工具。 文章目录 一、晕渲地貌工具1. 符号系统2. 栅格函数二、山体阴影效果1. 工具箱2. 栅格函数打开ArcGIS Pro3.0,加…...
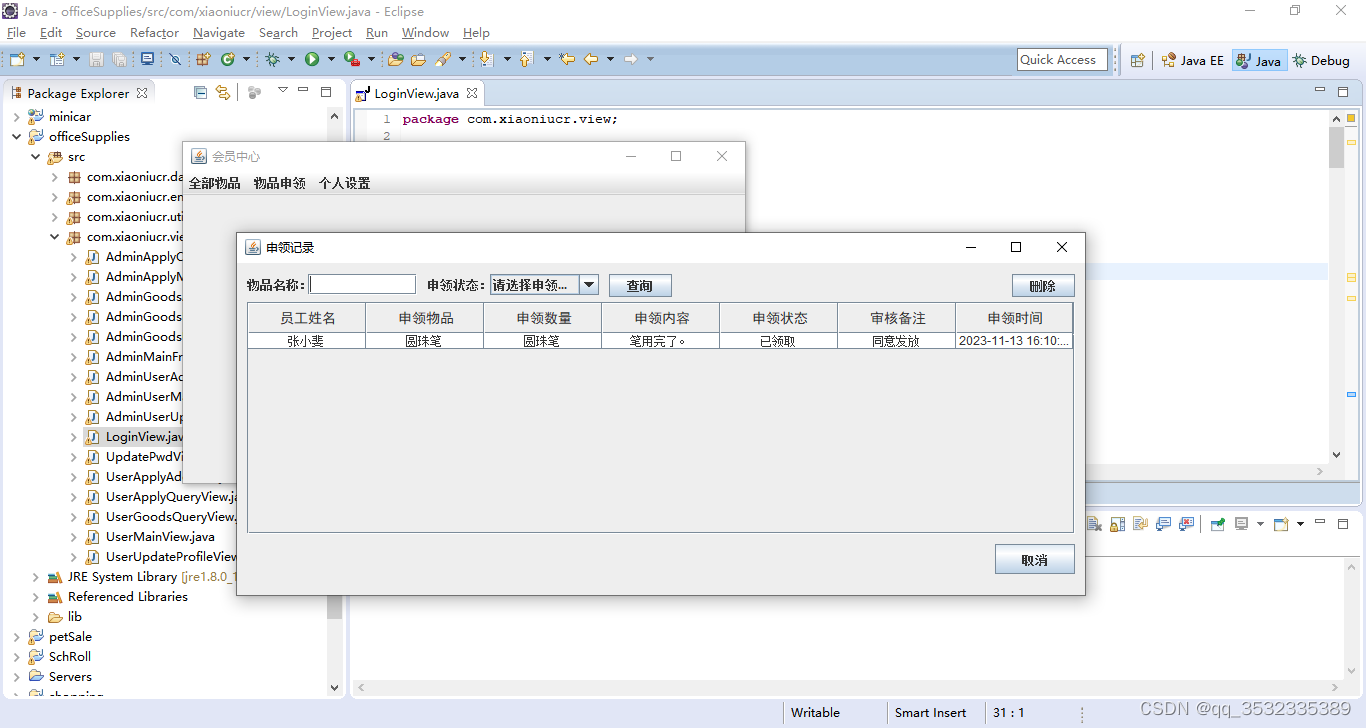
【原创】java+swing+mysql办公用品管理系统设计与实现
摘要: 办公用品管理系统是一个设计和实现办公用品库存和使用管理的信息系统。此系统可以提高办公用品的利用率,减少浪费,使办公用品管理更加高效、规范、便捷。本文主要介绍使用javaswingmysql技术去开发实现一个办公用品管理系统。 功能分…...

sqlalchemy查询数据为空,查询范围对应的数据在数据库真实存在
记录一个开发过程遇到的小bug,构造些伪数据还原并解释。 """ 场景:传参触发了查询条件,数据库中是存在传参对应范围的数据,但是通过查询条件得到的查询结果为空 """ 入参场景一: start_time = "2023-11-13" end_time = "202…...

Code Former安装及使用
Code Former是南洋理工大学和商汤科技联合研究中心联合开发一款AI人脸修复算法,通过该算法,可以对已经模糊的图片进行人脸修复,找回斑驳的记忆 由于网上对于Code Former的封装,全都是要花钱,或者需要其他什么曲折的方式…...

SpringMVC--@RequestMapping注解
RequestMapping注解 RequestMapping注解的功能RequestMapping注解的位置RequestMapping注解的属性1、value属性2、method属性3、params属性(了解) 补充RequestParamRequestHeaderRequestBody RequestBody获取json格式的请求参数 ResponseBodyRestControl…...
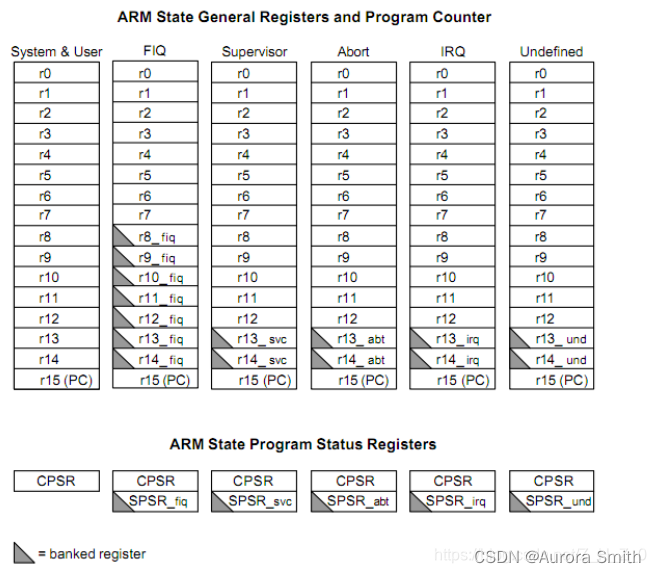
ARM寄存器及功能介绍/R0-R15寄存器
1、ARM 寄存器组介绍 ARM 处理器一般共有 37 个寄存器,其中包括: (1) 31 个通用寄存器,包括 PC(程序计数器)在内,都是 32 位的寄存器。 (2) 6 个状态寄存器…...
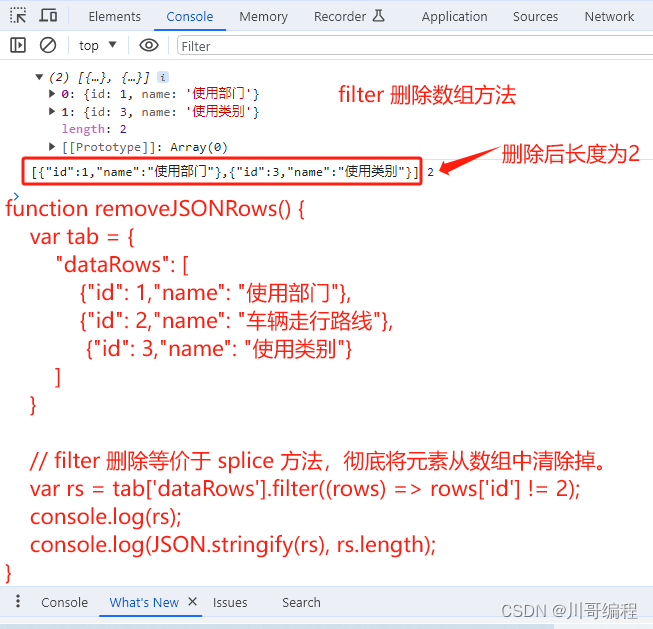
js删除json数据中指定元素
delete 删除数组方法: function removeJSONRows() {var tab {"dataRows": [{"id": 1,"name": "使用部门"},{"id": 2,"name": "车辆走行路线"},{"id": 3,"name": &quo…...

广州华锐互动:VR刑侦现场执法实训助力警察全面提升警务能力
随着科技的不断发展,虚拟现实(VR)技术在多个领域开始得到广泛应用,其中包括公安执法培训。VR刑侦现场执法实训系统是一种采用虚拟现实技术,为公安执法人员提供模拟真实环境的培训工具。通过这种平台,公安人…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
