K-means(K-均值)算法
K-means(k-均值,也记为kmeans)是聚类算法中的一种,由于其原理简单,可解释强,实现方便,收敛速度快,在数据挖掘、聚类分析、数据聚类、模式识别、金融风控、数据科学、智能营销和数据运营等领域有着广泛的应用。
K-means 是我们最常用的基于欧式距离的聚类算法,其认为两个目标的距离越近,相似度越大。
一、K-means基础
1.1牧师-村民模型
K-means 有一个著名的解释:牧师—村民模型:
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
我们可以看到该牧师的目的是为了让每个村民到其最近中心点的距离和最小。
1.2聚类
什么是聚类?
通俗说,聚类是将一堆数据划分成到不同的组中。
聚类(Clustering)的通俗定义:将一堆数据划分到不同的组中。一种无监督学习,其产生的类别是未知的。
聚类的学术定义:把一个数据对象的集合划分成簇(子集),使簇内对象彼此相似,簇间对象不相似的过程。
1.3聚类分类

在聚类算法中,常用的是 K-means 和 DBSCAN,但本文聚焦 K-means 。
HMM即隐马尔可夫模型(HiddenMarkovModel)在语音识别、机器翻译、中文分词、命名实体识别、词性标注、基因识别等领域有广泛的使用。
1.4基于划分的聚类算法
学术性的定义:按照某种目标将数据划分成若干个组,划分的结果是使目标函数值最大化(或最小化)。
通俗性的定义:根据样本特征的相似度或距离远近,将其划分为若干个类。
1.4.1相似度
什么是相似度?即两个对象的相似程度。
| 原理 | 代表 | |
|---|---|---|
| 基于距离的度量 | 距离小,相似度大 | 欧氏距离 |
| 基于夹角的度量 | 夹角小,相似度大 | 余弦相似度 |
1.4.2距离
什么是距离?即两点的距离。

二、K-means原理
K-means,其中K是指类的数量,means是指均值。
2.1K-means原理
K-means是基于样本集合划分的聚类算法,是一种无监督学习。
K-means的思想:
- 将样本集合划分为k个子集,构成k个类;
- 将n个样本分到k个类中,每个样本到其所属类的中心距离最小。
K-means的假设:一个样本只属于一个类,或者类的交集为空集。
K-means是怎么判断类别的,又是怎么判断相似的?

通过K-means算法原理,可知K-means的本质是物以类聚。
2.2K-means算法
K-means 的算法步骤为:
- 选择初始化的 k 个样本作为初始聚类中心
;
- 针对数据集中每个样本
计算它到 k 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中;
- 针对每个类别
,重新计算它的聚类中心
(即属于该类的所有样本的质心);
- 重复上面 2 3 两步操作,直到达到某个中止条件(迭代次数、最小误差变化等)。
K-means聚类算法的主要步骤:
- 第一步:初始化聚类中心:随机选取k个样本作为初始的聚类中心。(k需要提前确定)
- 第二步:给聚类中心分配样本:计算每个样本与各个聚类中心之间的距离,把每个样本分配给距离它最近的聚类中心(初始中心的选择影响聚类结果)
- 第三步:移动聚类中心 :新的聚类中心移动到这个聚类所有样本的平均值处(可能存在空簇)
- 第四步:停止移动:重复第2步,直到聚类中心不再移动为止
注意:K-means算法采用的是迭代的方法,得到局部最优解
2.2.1. K-means如何确定 K 值?
K-means 常常根据 SSE 和轮廓系数确定 K 值。
方法一:尝试不同k值:多选取几个k值,对比聚类效果,选择最优的k值。
方法二:结合业务特点:假定想要把文章分为兵乒球,篮球,综合三个类型,就设定k=3。
方法三:根据SSE和轮廓系数:SSE越小,聚类效果越好;轮廓系数越大,聚类效果越好。
2.2.2. K-means如何选取初始中心点?
K-means选择不同的初始中心,会得到不同的聚类结果。
K-means 常使用 K-means++ 方法确定初始中心点。
K-means++:选择初始的聚类中心之间的相互距离要尽可能的远。
二分K-means:选择误差最大的类,进行二分分裂。
2.2.3. K-means如何处理空簇?
聚类中心没有被分配到样本,常常将其删除。
空簇问题:K-means中计划聚成20类,结果才聚成19类,1类为空。
空簇原因:聚类中心没有被分配到样本。
解决办法:
- 法一:其他簇心的均值点
- 法二:删除空族
- 法三:最远离聚类中心的点
2.3. K- means特征工程
类别特征、大数值特征都不适用于 K-means 聚类。
原因:K-means是基于距离的,而类别没有距离。
k-means对异常值明显,比如年龄、金额等。
2.4. K- means评估
什么样的 K-means 聚类才是好的 K-means 聚类?
实际应用中,常常把 SSE(Sum of Squared Errors,误差平方和) 与轮廓系数(Silhouette Coefficient)结合使用,评估聚类模型的效果。
SSE:误差平方和(Sum of Squared Errors)最小,聚类效果最好。
轮廓系数(Silhouette Coefficient):轮廓系数越大,聚类效果越好。
2.4.1. SSE
SSE越小,聚类效果越好。

2.4.2. 轮廓系数
轮廓系数越大,聚类效果越好。

2.5复杂度
先看下伪代码:
获取数据 n 个 m 维的数据
随机生成 K 个 m 维的点
while(t)for(int i=0;i < n;i++)for(int j=0;j < k;j++)计算点 i 到类 j 的距离for(int i=0;i < k;i++)1. 找出所有属于自己这一类的所有数据点2. 把自己的坐标修改为这些数据点的中心点坐标
end时间复杂度: ,其中,t 为迭代次数,k 为簇的数目,n 为样本点数,m 为样本点维度。
空间复杂度: ,其中,k 为簇的数目,m 为样本点维度,n 为样本点数。
三、K-means应用
3.1K-means的python实现
# -*- coding:utf-8 -*-
import numpy as np
from matplotlib import pyplotclass K_Means(object):# k是分组数;tolerance‘中心点误差’;max_iter是迭代次数def __init__(self, k=2, tolerance=0.0001, max_iter=300):self.k_ = kself.tolerance_ = toleranceself.max_iter_ = max_iterdef fit(self, data):self.centers_ = {}for i in range(self.k_):self.centers_[i] = data[i]for i in range(self.max_iter_):self.clf_ = {}for i in range(self.k_):self.clf_[i] = []# print("质点:",self.centers_)for feature in data:# distances = [np.linalg.norm(feature-self.centers[center]) for center in self.centers]distances = []for center in self.centers_:# 欧拉距离# np.sqrt(np.sum((features-self.centers_[center])**2))distances.append(np.linalg.norm(feature - self.centers_[center]))classification = distances.index(min(distances))self.clf_[classification].append(feature)# print("分组情况:",self.clf_)prev_centers = dict(self.centers_)for c in self.clf_:self.centers_[c] = np.average(self.clf_[c], axis=0)# '中心点'是否在误差范围optimized = Truefor center in self.centers_:org_centers = prev_centers[center]cur_centers = self.centers_[center]if np.sum((cur_centers - org_centers) / org_centers * 100.0) > self.tolerance_:optimized = Falseif optimized:breakdef predict(self, p_data):distances = [np.linalg.norm(p_data - self.centers_[center]) for center in self.centers_]index = distances.index(min(distances))return indexif __name__ == '__main__':x = np.array([[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]])k_means = K_Means(k=2)k_means.fit(x)print(k_means.centers_)for center in k_means.centers_:pyplot.scatter(k_means.centers_[center][0], k_means.centers_[center][1], marker='*', s=150)for cat in k_means.clf_:for point in k_means.clf_[cat]:pyplot.scatter(point[0], point[1], c=('r' if cat == 0 else 'b'))predict = [[2, 1], [6, 9]]for feature in predict:cat = k_means.predict(predict)pyplot.scatter(feature[0], feature[1], c=('r' if cat == 0 else 'b'), marker='x')pyplot.show()运行结果如下:
{0: array([1.16666667, 1.46666667]), 1: array([7.33333333, 9. ])} 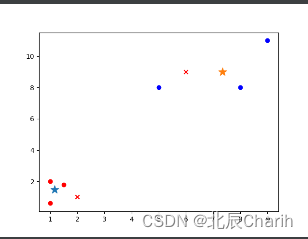
备注:*是两组数据的”中心点”;x是预测点分组。
3.2K-means的Sklearn实现
import numpy as np
from sklearn.cluster import KMeans
from matplotlib import pyplotif __name__ == '__main__':x = np.array([[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]])# 把上面数据点分为两组(非监督学习)
clf = KMeans(n_clusters=2)
clf.fit(x) # 分组centers = clf.cluster_centers_ # 两组数据点的中心点
labels = clf.labels_ # 每个数据点所属分组
print(centers)
print(labels)for i in range(len(labels)):pyplot.scatter(x[i][0], x[i][1], c=('r' if labels[i] == 0 else 'b'))
pyplot.scatter(centers[:, 0], centers[:, 1], marker='*', s=100)# 预测
predict = [[2, 1], [6, 9]]
label = clf.predict(predict)
for i in range(len(label)):pyplot.scatter(predict[i][0], predict[i][1], c=('r' if label[i] == 0 else 'b'), marker='x')pyplot.show()运行结果如下:
[[7.33333333 9. ][1.16666667 1.46666667]]
[1 1 0 0 1 0]
备注:*是两组数据的”中心点”;x是预测点分组。
3.3. 用户聚类分群
数据集:titanic.xls(泰坦尼克号遇难者与幸存者名单)
titanic.xls的数据集获取地址:
titanic.xls
任务:基于除survived字段外的数据,使用k-means对用户进行分组(生/死)


聚类的用户分群常用在早期,尝试进行用户探索。实际落地常常结合用户标签,或者用户画像进行用户分群。
用户聚类分群的python代码如下:
# -*- coding:utf-8 -*-
import numpy as np
from sklearn.cluster import KMeans
from sklearn import preprocessing
import pandas as pd# 加载数据
df = pd.read_excel('titanic.xls')
df.drop(['body', 'name', 'ticket'], 1, inplace=True)
df.fillna(0, inplace=True) # 把NaN替换为0# 把字符串映射为数字,例如{female:1, male:0}
df_map = {}
cols = df.columns.values
for col in cols:if df[col].dtype != np.int64 and df[col].dtype != np.float64:temp = {}x = 0for ele in set(df[col].values.tolist()):if ele not in temp:temp[ele] = xx += 1df_map[df[col].name] = tempdf[col] = list(map(lambda val: temp[val], df[col]))# 将每一列特征标准化为标准正太分布
x = np.array(df.drop(['survived'], 1).astype(float))
x = preprocessing.scale(x)
clf = KMeans(n_clusters=2)
clf.fit(x)# 计算分组准确率
y = np.array(df['survived'])
correct = 0
for i in range(len(x)):predict_data = np.array(x[i].astype(float))predict_data = predict_data.reshape(-1, len(predict_data))predict = clf.predict(predict_data)if predict[0] == y[i]:correct += 1print(correct * 1.0 / len(x))执行结果:
第一次执行:0.6974789915966386
第二次执行:0.3017570664629488
注意:结果出现很大波动,原因是它随机分配组(生:0,死:1)(生:1,死:0)。
四、K-means总结
4.1K-means的优缺点
4.1.1优点
- 容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了;
- 原理简单,实现方便,收敛速度快;
- 处理大数据集的时候,该算法可以保证较好的伸缩性;
- 当簇近似高斯分布的时候,效果非常不错;
- 算法复杂度低;
- 聚类效果较优;
- 模型的可解释性较强;
- 调参只需要调类数k 。
4.1.2 缺点
- K 值需要人为设定,不同 K 值得到的结果不一样,k的选取不好把握;
- 对初始的簇中心敏感,不同选取方式会得到不同结果;
- 对异常值敏感;
- 样本只能归为一类,不适合多分类任务;
- 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类;
- 如果数据的类型不平衡,则聚类效果不佳
- 采用的是迭代的方法,得到局部最优解
- 对于噪音和异常点比较敏感
什么是凸集 (convex set)?
凸集 (convex set)
欧几里得空间的一个子集,其中任意两点之间的连线仍完全落在该子集内。例如,下面的两个图形都是凸集:
所以,凸的数据集,即数据集的样本呈现凸集分布。
相反,下面的两个图形都不是凸集:
所以,不是凸的数据集,即是数据集的样本呈现的不是凸集分布。
4.2K-means的改进
针对K-means缺点,K-means有许多改进算法,如数据预处理(去除异常点),合理选择 K 值,高维映射等。
| 缺点 | 改进 |
|---|---|
| 1、k的选取不好把握 | ISODATA |
| 2、对初始聚类中心敏感 | k-means++ |
| 3、对于不是凸的数据集比较难以收敛 | DESCAN |
| 4、如果数据的类型不平衡,则聚类效果不佳 | CUSBoost |
| 5、采用的是迭代的方法,得到局部最优解 | 二分K-means |
| 6、对于噪音和异常点比较敏感 | K-Mediods |
【机器学习】K-means(非常详细) - 知乎 (zhihu.com) https://zhuanlan.zhihu.com/p/78798251
https://zhuanlan.zhihu.com/p/78798251
Kmeans++聚类算法原理与实现 - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/152286357
https://zhuanlan.zhihu.com/p/152286357
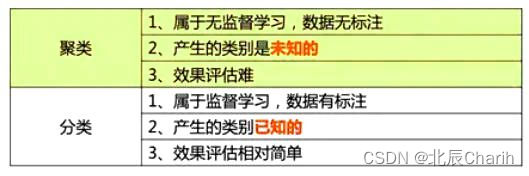
4.3聚类和分类的区别
聚类和分类的区别是什么呢?
最大区别是:聚类是无监督的;分类是有监督学习。
其中机器学习的分类按输出类别(标签)不同,可以分为二分类(Binary Classification)、多分类(Multi-Class Classification)、多标签分类(Multi-Label Classification)。
相关文章:

K-means(K-均值)算法
K-means(k-均值,也记为kmeans)是聚类算法中的一种,由于其原理简单,可解释强,实现方便,收敛速度快,在数据挖掘、聚类分析、数据聚类、模式识别、金融风控、数据科学、智能营销和数据运…...

网络安全自学
前言 一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防…...
加速mvn下载seatunnel相关jar包
seatunnel安装的时候,居然要使用mvnw来下载jar包,而且是从https://repo.maven.apache.org 下载,速度及其缓慢,改用自己本地的mvn下载。 修改其安装插件相关脚本,复制install-plugin.sh重命名为install-plugin-mvn.sh …...
:用于计算非支配(non-dominated)前沿)
【函数讲解】botorch中的函数 is_non_dominated():用于计算非支配(non-dominated)前沿
# 获取训练目标值,计算Pareto前沿(非支配解集合),然后从样本中提取出Pareto最优解。train_obj self.samples[1]pareto_mask is_non_dominated(train_obj)pareto_y train_obj[pareto_mask] 源码 这里用到了一个函数 is_non_dom…...
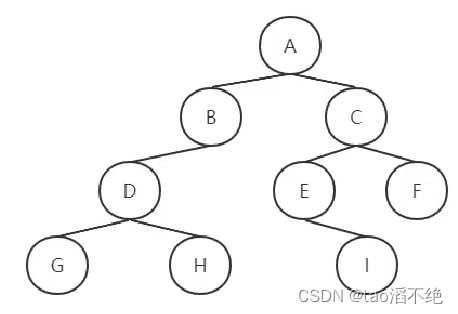
LeetCode题94,44,145,二叉树的前中后序遍历,非递归
注意:解题都要用到栈 一、前序遍历 题目要求 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,2,3]示例 2: 输入:root [] 输出:[…...
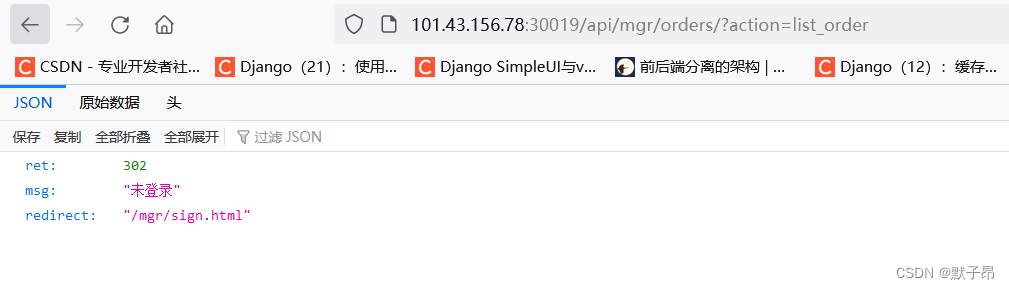
Python 框架学习 Django篇 (九) 产品发布、服务部署
我们前面编写的所有代码都是在windows上面运行的,因为我们还处于开发阶段 当我们完成具体任务开发后,就需要把我们开发的网站服务发布给真正的用户 通常来说我们会选择一台公有云服务器比如阿里云ecs,现在的web服务通常都是基于liunx操作系统…...

Git 服务器上的 LFS 下载
以llama为例: https://huggingface.co/meta-llama/Llama-2-7b-hf Github # 1. 安装完成后,首先先初始化;如果有反馈,一般表示初始化成功 git lfs install # 2. 如果刚刚下载的那个项目没啥更改,重新下一遍&#x…...

Canvas和SVG:你应该选择哪一个?
如果你是一个Web开发者,你可能已经听说过Canvas和SVG。这两种技术都可以用来创建图形和动画,但它们有什么区别?在这篇文章中,我们将探讨Canvas和SVG的区别以及它们的应用场景,帮助你决定哪种技术更适合你的项目。 什么…...

openGauss学习笔记-122 openGauss 数据库管理-设置密态等值查询-密态支持函数/存储过程
文章目录 openGauss学习笔记-122 openGauss 数据库管理-设置密态等值查询-密态支持函数/存储过程122.1 创建并执行涉及加密列的函数/存储过程 openGauss学习笔记-122 openGauss 数据库管理-设置密态等值查询-密态支持函数/存储过程 密态支持函数/存储过程当前版本只支持sql和P…...

BEVFormer 论文阅读
论文链接 BEVFormer BEVFormer,这是一个将Transformer和时间结构应用于自动驾驶的范式,用于从多相机输入中生成鸟瞰(BEV)特征利用查询来查找空间/时间,并相应地聚合时空信息,从而为感知任务提供更强的表示…...
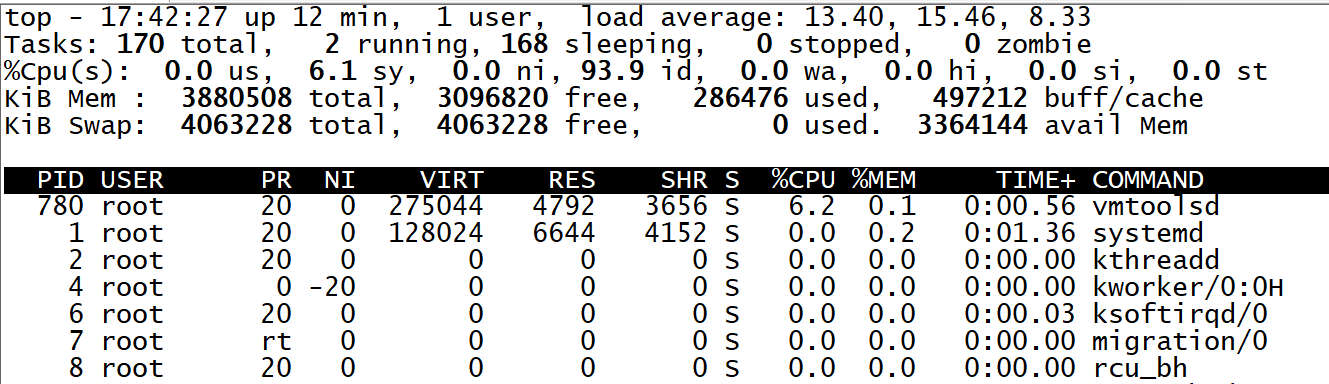
Centos批量删除系统重复进程
原创作者:运维工程师 谢晋 Centos批量删除系统重复进程 客户一台CENTOS 7系统负载高,top查看有很多sh的进程,输入命令top -c查看可以看到对应的进程命令是/bin/bash 经分析后发现是因为该脚本执行时间太长,导致后续执…...
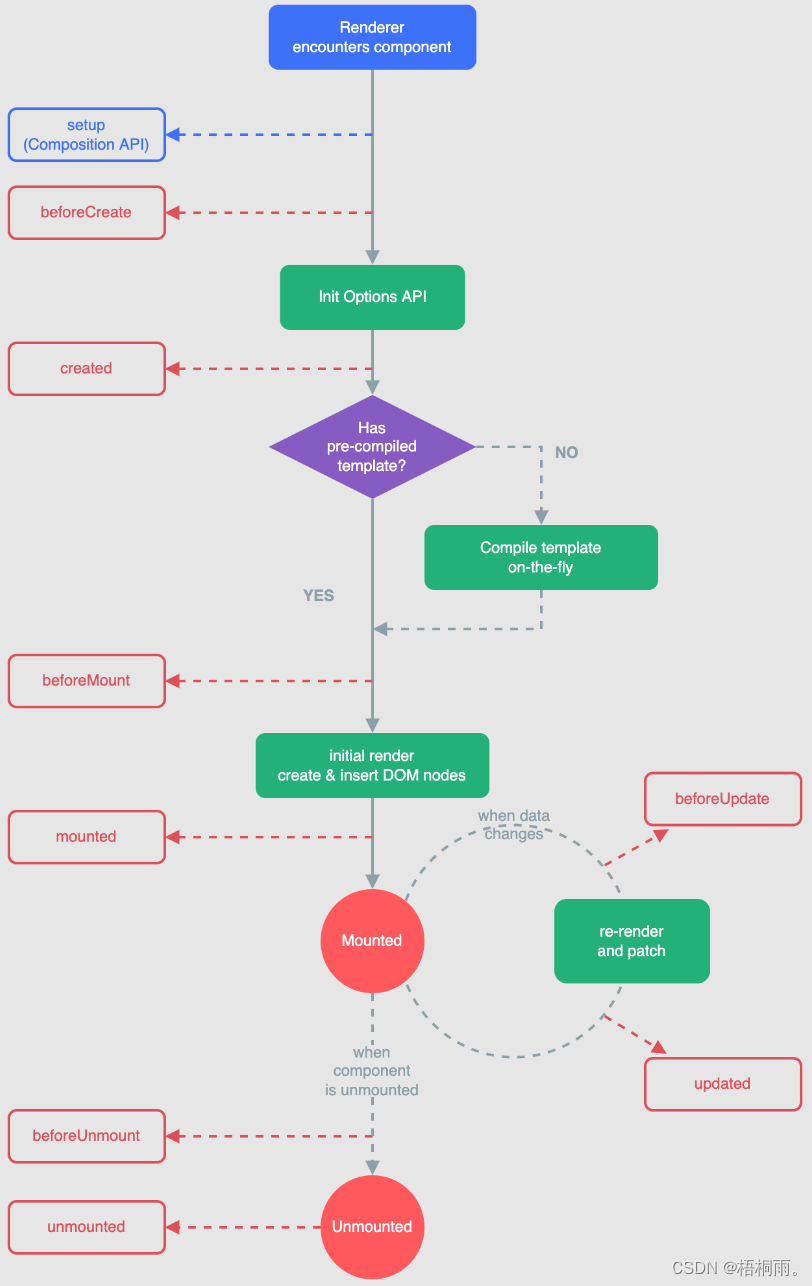
VUE组件的生命周期
每个 Vue 组件实例在创建时都需要经历一系列的初始化步骤,比如设置好数据侦听,编译模板,挂载实例到 DOM,以及在数据改变时更新 DOM。在此过程中,它也会运行被称为生命周期钩子的函数,让开发者有机会在特定阶…...

【Git系列】Github指令搜索
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

【OpenCV】用数组给Mat图像赋值,单/双/三通道 Mat赋值
文章目录 5 Mat赋值5.1 Mat(int rows, int cols, int type, const Scalar& s)5.2 数组赋值 或直接赋值5.2.1 3*3 单通道 img5.2.2 3*3 双通道 img5.2.3 3*3 三通道 img5 Mat赋值 5.1 Mat(int rows, int cols, int type, const Scalar& s) Mat m(3, 3, CV_8UC3,Scalar…...
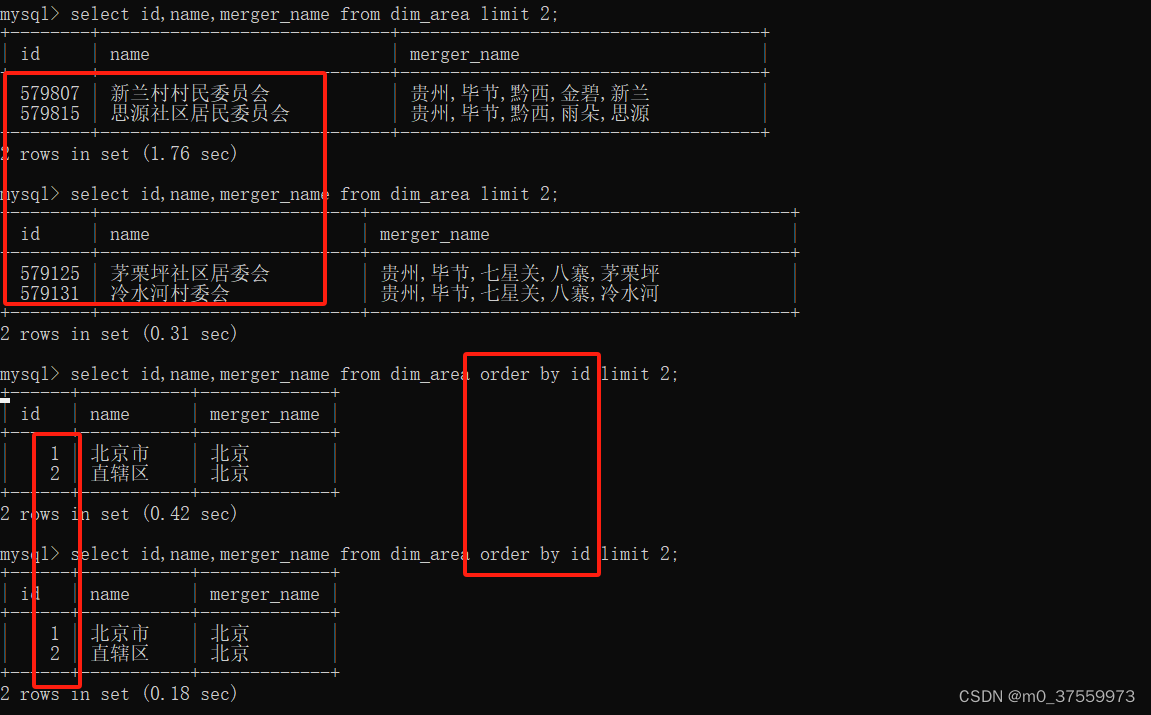
Doris:读取Doris数据的N种方法
目录 1.MySQL Client 2.JDBC 3. 查询计划 4.Spark Doris Connector 5.Flink Doris Connector 1.MySQL Client Doris 采用 MySQL 协议,高度兼容 MySQL 语法,支持标准 SQL,用户可以通过各类客户端工具来访问 Doris。登录到doris服务器后&a…...

ceph-deploy bclinux aarch64 ceph 14.2.10
ssh-copy-id,部署机免密登录其他三台主机 所有机器硬盘配置参考如下,计划采用vdb作为ceph数据盘 下载ceph-deploy pip install ceph-deploy 免密登录设置主机名 hostnamectl --static set-hostname ceph-0 .. 3 配置hosts 172.17.163.105 ceph-0 172.…...
:使用lxml抓取相亲信息)
爬虫项目(13):使用lxml抓取相亲信息
文章目录 书籍推荐完整代码效果书籍推荐 如果你对Python网络爬虫感兴趣,强烈推荐你阅读《Python网络爬虫入门到实战》。这本书详细介绍了Python网络爬虫的基础知识和高级技巧,是每位爬虫开发者的必读之作。详细介绍见👉: 《Python网络爬虫入门到实战》 书籍介绍 完整代码…...

mysql-数据库三大范式是什么、mysql有哪些索引类型,分别有什么作用 、 事务的特性和隔离级别
1. 数据库三大范式是什么? 数据库三大范式是设计关系型数据库时的规范化原则,确保数据库结构的合理性和减少数据冗余。 这三大范式分别是: - **第一范式(1NF):** 数据表中的所有列都是不可分割的原子数据项…...
微信小程序案例3-2 计算器
文章目录 一、运行效果二、知识储备(一)data-*自定义属性(二)模块 三、实现步骤(一)准备工作1、创建项目2、设置导航栏 (二)实现页面结构1、编写页面整体结构2、编写结果区域的结构3…...
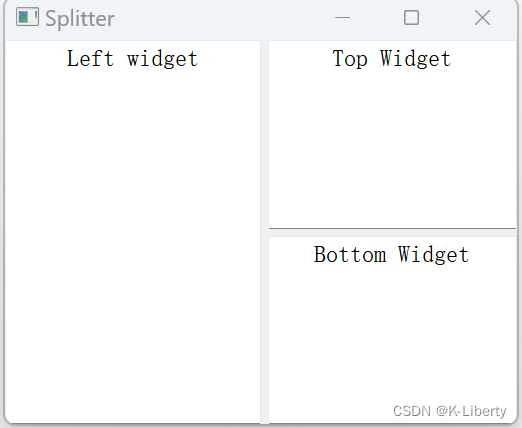
QT QSplitter
分裂器QSplitter类提供了一个分裂器部件。和QBoxLayout类似,可以完成布局管理器的功能,但是包含在它里面的部件,默认是可以随着分裂器的大小变化而变化的。 比如一个按钮放在布局管理器中,它的垂直方向默认是不会被拉伸的,但是放到分裂器中就可以被拉伸。还有一点不…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...