浅谈二叉树

✏️✏️✏️今天给大家分享一下二叉树的基本概念以及性质、二叉树的自定义实现,二叉树的遍历等。
清风的CSDN博客
😛😛😛希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流!
动动你们发财的小手,点点关注点点赞!在此谢过啦!哈哈哈!😛😛😛
✏️✏️✏️如果觉得我分享和内容还不错的话,可以给我一个小小的赞吗?

好,废话不多说,我们直接进入正题!!!
目录
一、树形结构
1.1 概念
1.2 关于树的一些概念术语
1.3 树的表示形式
1.4 树的应用
二、二叉树
2.1 概念
2.2 两种特殊的二叉树
2.3 二叉树的重要性质
2.4 二叉树的存储
2.5 二叉树的基本操作
2.5.1 二叉树的类定义
2.5.2 二叉树的创建
2.5.3 二叉树的前序遍历
2.5.4 二叉树的中序遍历
2.5.5 二叉树的后序遍历
2.5.6 获取树中节点个数
2.5.7 获取叶子节点个数
2.5.8 获取第K层节点个数
2.5.9 获取二叉树的高度
2.5.10 查找二叉树中是否存在值为val的节点
一、树形结构
1.1 概念
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。


注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 关于树的一些概念术语

1.3 树的表示形式
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
1.4 树的应用

二、二叉树
2.1 概念

- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

2.2 两种特殊的二叉树
完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一 一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3 二叉树的重要性质
5.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
2.4 二叉树的存储
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}2.5 二叉树的基本操作
2.5.1 二叉树的类定义
public class BinaryTree {static public class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val){this.val=val;}}
}2.5.2 二叉树的创建
二叉树是递归定义的,因此可以通过递归来创建一颗二叉树,也可以通过穷举法来创建。我们先通过穷举法来创建,后续我会给大家分享递归创建二叉树。
public TreeNode CreatBinaryTree(){TreeNode A=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode C=new TreeNode('C');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');TreeNode H=new TreeNode('H');A.left=B;A.right=C;B.left=D;B.right=E;C.left=F;C.right=G;D.left=H;return A;}通过上面的穷举法,我们就创建了下面这样一棵二叉树:

2.5.3 二叉树的前序遍历
递归遍历:
public void preOrder(TreeNode root){if(root==null){return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}非递归遍历:
public void preOrderNor(TreeNode root){Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null || !stack.empty()){while(cur!=null){System.out.print(cur.val+" ");stack.push(cur);cur=cur.left;}TreeNode top = stack.pop();cur=top.right;}}2.5.4 二叉树的中序遍历
递归遍历:
public void inOrder(TreeNode root){if(root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}非递归遍历:
public void inOrderNor(TreeNode root){Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;while(cur!=null || !stack.empty()){while(cur!=null){stack.push(cur);cur=cur.left;}TreeNode top=stack.pop();System.out.print(top.val+" ");cur=top.right;}}2.5.5 二叉树的后序遍历
递归遍历:
public void postOrder(TreeNode root){if(root==null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}非递归遍历:
public void postOrderNor(TreeNode root){Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;TreeNode prev=null;while(cur!=null || !stack.empty()){while(cur!=null){stack.push(cur);cur=cur.left;}TreeNode top=stack.peek();if(top.right==null || top.right==prev){System.out.print(top.val+" ");stack.pop();prev=top;//记录最新被打印的节点}else{cur=top.right;}}}2.5.6 获取树中节点个数
public int size(TreeNode root){if(root==null){return 0;}return size(root.left)+size(root.right)+1;}2.5.7 获取叶子节点个数
public int getLeafNodeCount(TreeNode root){if(root==null){return 0;}if(root.left==null && root.right==null){return 1;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}2.5.8 获取第K层节点个数
public int getKLevelNodeCount(TreeNode root,int k){if(root==null){return 0;}if(k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}2.5.9 获取二叉树的高度
public int getHeight(TreeNode root){if(root==null){return 0;}/* if(root.left==null && root.right==null){return 1;}*/int leftHeight=getHeight(root.left);int rightHeight=getHeight(root.right);return leftHeight > rightHeight ? leftHeight+1:rightHeight+1;}2.5.10 查找二叉树中是否存在值为val的节点
TreeNode find(TreeNode root, char val){if(root==null){return null;}if(root.val==val){return root;}TreeNode ret1=find(root.left,val);if(ret1!=null){return ret1;}TreeNode ret2=find(root.right,val);if(ret2!=null){return ret2;}return null;}✨希望各位看官读完文章后,能够有所提升。
🎉好啦,今天的分享就到这里!!
✨创作不易,还希望各位大佬支持一下!
👍点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论:你的意见是我进步的财富!

相关文章:

浅谈二叉树
✏️✏️✏️今天给大家分享一下二叉树的基本概念以及性质、二叉树的自定义实现,二叉树的遍历等。 清风的CSDN博客 😛😛😛希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流&…...
 用QWebSocket 实现服务端和客户端(详细代码直接使用))
(二) 用QWebSocket 实现服务端和客户端(详细代码直接使用)
目录 前言 一、服务器的代码: 1、服务器的思路 2、具体服务器的代码示例 二、客户端的代码: 1、客户端的思路(和服务器类似) 2、具体客户端的代码示例 前言 要是想了解QWebSocket的详细知识,还得移步到上一篇文…...

关于我在配置zookeeper出现,启动成功,进程存在,但是查看状态却没有出现Mode:xxxxx的问题和我的解决方案
在我输入:zkServer.sh status 之后出现报错码. 报错码: ZooKeeper JMX enabled by default Using config: /opt/software/zookeeper/bin/../conf/zoo.cfgClient port found: 2181. Client address: localhost. Error contacting service. It is probably not runni…...

react及相关面试问题汇总
目录 1、什么是React?它的特点是什么? 2、解释一下虚拟DOM(Virtual DOM)的概念以及它的工作原理。 3、什么是组件(Component)?如何定义一个React组件? 4、什么是JSX?它与HTML的区别是什么?如何在React中…...

QT4到QT5移植出现的一些问题
转自:QT4到QT5移植出现的一些问题_西门子3gl qt5 许可证-CSDN博客 在上述作者基础上修改: 一、问题1:头文件的问题 1、QtGui/QApplication: No such file or directory 1.1错因 原因是Qt5源文件位置的改动 1.2解决 pro文件里࿰…...
【可解释AI】Alibi explain: 解释机器学习模型的算法
Alibi explain: 解释机器学习模型的算法 可解释人工智能简介Alibi特点算法Library设计展望参考资料 今天介绍Alibi Explain,一个开源Python库,用于解释机器学习模型的预测(https://github.com/SeldonIO/alibi)。该库具有最先进的分类和回归模型可解释性算…...

No191.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

ROS基础—vscode创建工作空间
1、创建ROS工作空间 首先打开ubuntu的终端,接着依次输入如下的命令行; mkdir -p xxx_ws/src(必须得有 src) cd xxx_ws catkin_make当然我一般是新建一个叫做demo的工作空间,如 mkdir -p demo04_ws/src 2、启动vscode cd xxx_ws code . …...
)
机器学习复习(待更新)
01绪论 (1)机器学习基本分类: 监督学习(有标签)半监督学习(部分标签,找数据结构)无监督学习(无标签,找数据结构)强化学习(不断交互&…...
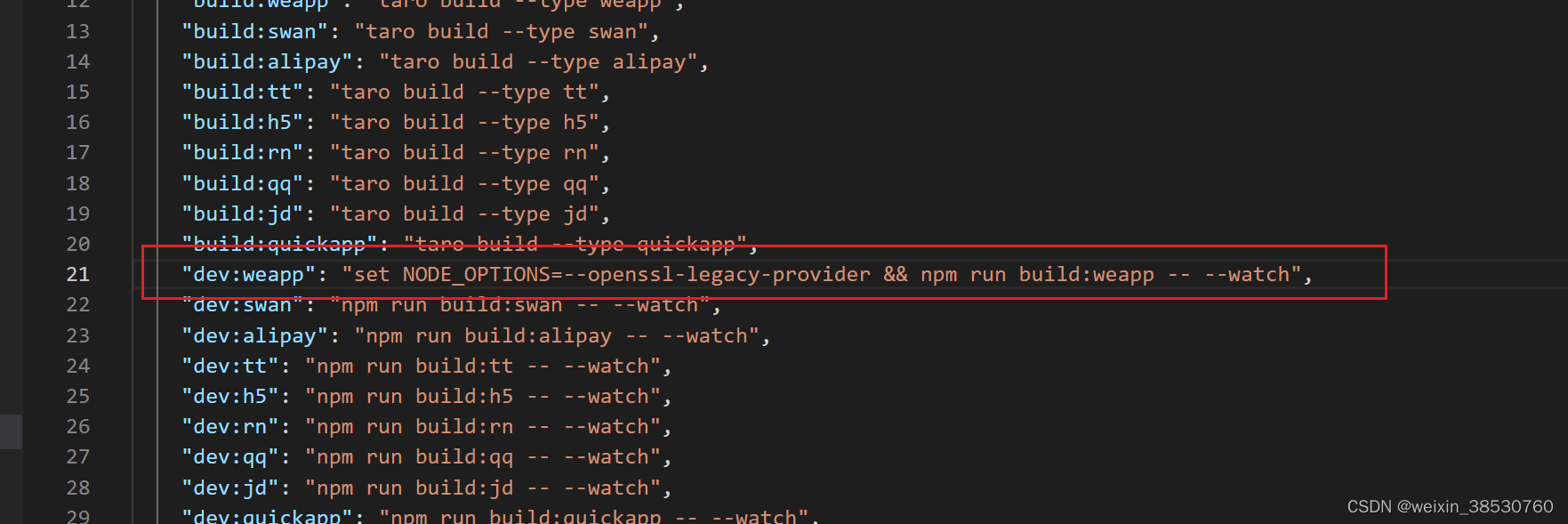
taro(踩坑) npm run dev:weapp 微信小程序开发者工具预览报错
控制台报错信息: VM72:9 app.js错误: Error: module vendors-node_modules_taro_weapp_prebundle_chunk-JUEIR267_js.js is not defined, require args is ./vendors-node_modules_taro_weapp_prebundle_chunk-JUEIR267_js.js 环境: node 版本&#x…...

3. 深度学习——损失函数
机器学习面试题汇总与解析——损失函数 本章讲解知识点 什么是损失函数?为什么要使用损失函数?详细讲解损失函数本专栏适合于Python已经入门的学生或人士,有一定的编程基础。 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。 本专栏针对面试题答案进行了优化…...

交叉编译 openssl
要在 x86 平台上编译适用于 aarch64 架构的 OpenSSL 动态库,你需要使用交叉编译工具链。可以按照以下步骤进行: 安装 aarch64 交叉编译工具链: $ sudo apt-get install gcc-aarch64-linux-gnu g-aarch64-linux-gnu 这将安装 aarch64 交叉编…...

C++文件的读取和写入
1、C对txt文件的读,ios::in #include<iostream> #include<fstream> using namespace std;int main() {ifstream ifs;ifs.open("test.txt",ios::in);if(!ifs.is_open()){cout<<"打开文件失败!"<<endl;}char…...

住宅IP、家庭宽带IP以及原生IP,它们有什么区别?谷歌开发者账号应选择哪种IP?
IP地址(Internet Protocol Address)是互联网协议地址的简称,是互联网通信的基础,互联网上每一个网络设备的唯一标识符每个在线的设备都需要一个IP地址,这样才能在网络中找到它们并进行数据交换。 IP地址有很多种类型&…...
--内存管理之I/O交换与性能调优)
Linux内核分析(十三)--内存管理之I/O交换与性能调优
目录 一、引言 二、page cache ------>2.1、file-backed ------>2.2、匿名页(Anonymous page) ------>2.3、读写方式 ------>2.4、常驻内存 三、页面回收 ------>3.1、LRU算法 ------>3.2、嵌入式系统的zRAM 四、内存性能调优 ------>4.1、存储…...

前端使用webscoket
前端 <template><div class"wrap"><button click"socketEmit">连接Socket</button><button click"socketSendmsg">发送数据</button></div> </template><script> export default {data(…...

centos安装Git
一开始使用yum -y install git出来的版本比较低。 1.yum安装gityum -y install git 2.查看git的版本git --version 3.删除git(版本过低)yum remove -y git 后来通过源码编译后安装: 使用安装包安装: 1.下载安装包:h…...
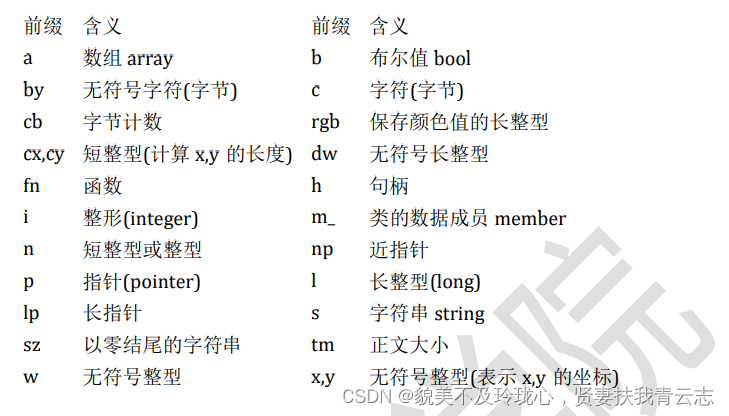
网络编程 初探windows编程
目录 一、什么是Winodws编程 二、开发环境搭建以及如何学习 三、VA助手安装 四、第一个Win32程序 五、窗口类句柄/窗口类对象 六、Winodws消息循环机制 七、Windows数据类型 一、什么是Winodws编程 Windows 编程指的是在 Microsoft Windows 操作系统上进行软件开发的过…...
Vue3 ref函数和reactive函数
一、ref函数 我们在setup函数中导出的属性和方法虽然能够在模板上展示出来,但是并没有给属性添加响应式,因此,我们需要使用ref函数来为我们的数据提供响应式。 (一)引入ref函数 import { ref } from "vue"…...

docker常用命令详解
1. Image常见操作 (1)查看本地image列表 docker images docker image ls (2)获取远端镜像 docker pull (3)删除镜像[注意此镜像如果正在使用,或者有关联的镜像,则需要先处理完] docker image rm imageid docker rmi -f imageid docker rmi -f $(docker …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
