傅里叶分析(2)
在《傅里叶分析(1)》中,讲述了连续信号的傅里叶分析方法,本文讲述离散信号的傅里叶分析方法。
虽然电、声、光、机械振动等信号在物理上是连续函数,但在实际工程中,其通常为离散信号,即若干离散的数据点。对于离散信号,傅里叶级数和傅里叶变换已经无法使用,需要使用 DTFT(离散时间傅里叶变换)和 DFT(离散傅里叶变换)分析离散信号。
1 离散信号的来源
离散信号来源于对连续信号的采样。数学处理上,离散信号为连续信号和采样函数(sampling function)的乘积:
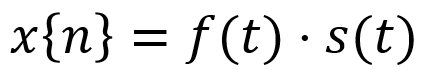
采样函数为基于狄拉克 δ 函数(Dirac delta function)表述的脉冲序列,其定义如下:

采样函数为周期函数,其在非采样时刻的函数值为 0,由此可得仅限采样时刻的离散数据点。
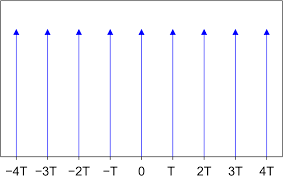
采样函数的图像(图源:维基百科)
采样函数的傅里叶变换为频域上的采样函数,其周期为 1/T:

2 离散时间傅里叶变换(discrete-time Fourier transform,DTFT)
根据前述采样方法,可将离散信号 x{n} 视为连续函数,除了采样点之外其他时刻函数值均为0。
傅里叶变换的卷积特性可表示为:

利用傅里叶变换的卷积特性,对 x{n} 进行傅里叶变换,其结果即 DTFT 计算公式为:

变换结果 X(ξ) 为连续周期函数,其周期为 1/T,即 X(ξ)=X(ξ+n/T)。
由于 X(ξ) 为连续函数,其逆变换可直接使用傅里叶逆变换的计算公式。对于周期函数,可将积分区间从无穷大简化到一个周期内,得到 DTFT 逆变换公式:

其中,积分区间可为任意的区间,只需满足区间的长度为单个周期长度 1/T 即可。根据 n 取值的不同即可获得 x{n} 各项取值。
对于纯实数的信号 x{n},其变换结果 X(ξ) 在正频率和负频率的幅值为对称关系。
3 离散傅里叶变换(discrete Fourier transform,DFT)
虽然 DTFT 表明了离散信号的频谱分析方法,但是得到的频谱是连续函数,对基于程序的实际信号分析造成很大困难。
引用 DTFT 思路,将 x{n} 视为连续函数。根据连续信号的频谱特征,周期函数的频谱为离散点,由此可对频谱进行程序处理。
将包含 N 个数据点的有限数据集 x{n}(从 x{0} 至 x{N-1}),进行周期延拓,即 x{n} = x{n+k*T*N)},可使之成为在无穷大区间均有定义的周期函数,其周期为 T*N。由于 x{n} 的周期性,对 x{n} 进行DTFT 仅需在单周期内即可进行。
单周期内的 DTFT 为 DFT,其计算公式为:

很显然,X{k} 在区间 [0, N-1] 只有 N 个取值,且周期为 N。
同理,在频域的单周期内进行 DTFT 逆变换,即可得到 DFT 逆变换计算公式:

4 重要问题
4.1 频谱的类型
通常而言,时域信号 x{n} 来源为传感器信号、A/D电路转换等,其表示的物理量通常为可直接测量的物理量,如速度、电流、温度等。
实际应用中,频谱通常分为幅值谱(amplitude spectrum)和功率谱(power spectrum)两类。幅值谱表示与功率的平方根成比例的物理量(如速度、电流、电压等);功率谱表示功率或与功率成比例的物理量(如光强度、声强度等)。

功率谱示意图(图源:mathworks.com)
幅值谱和功率谱分别定义如下:

4.2 频谱范围与精度
对于纯实数函数,在正数范围内,DFT 可分析的频率范围为:

其中,t 为采样总时间,fs 为采样频率。
由 DFT 周期延拓的操作思路即可得,信号的基频为采样总时间对应的频率,其他所有频率都高于基频。根据奈奎斯特采样定理(Nyquist sampling theorem),离散信号可分析的频谱最高频率为采样频率的一半。对于更高频率部分,DFT 已无法分析。
DFT 频谱的频率分辨率为:

其中 N 为信号的数据点数量。
4.2 数据处理与窗函数
对离散信号的周期延拓,通常会在信号首尾两端形成较大的不连续。信号在时域的不连续会导致频谱泄露(spectral leakage),即人为形成某些本不存在的谐波。
通过窗函数(window function)对离散信号进行处理,使信号首尾两端的幅值逐步降低,可降低信号在两端的不连续性。
通过窗函数处理后的信号 y{n} 和原始信号 x{n} 之间,满足:

其中 w{n} 为窗函数。
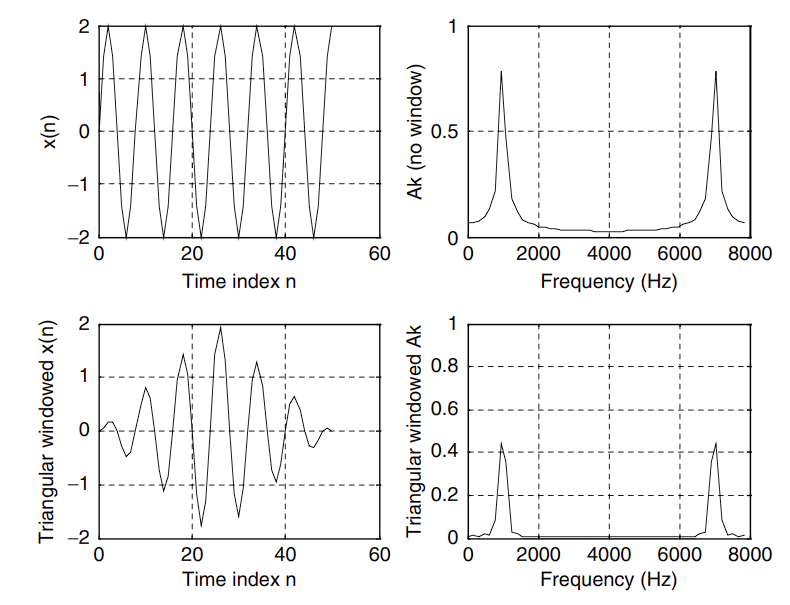
窗函数应用效果对比(图源:《Digital Signal Processing Fundamentals and Applications》,作者 Li Tan)
常用的窗函数包括三角、Hamming、Hanning等。
若信号是宽带信号,即不存在很明显的频域尖峰,可无需窗函数处理。Hanning 窗函数适用于多数常规问题,可作为通用的窗函数。
Hanning 窗函数表达式为:
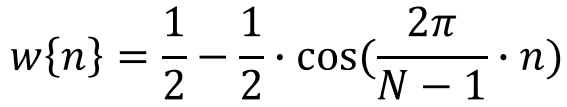
5 DFT 和 FFT 的关系
快速傅里叶变换(Fast Fourier Transform,FFT)是 DFT 的一种计算方法。FFT 本质上是利用其它替代计算方式,避免根据 DFT 的定义直接计算 DFT,从而加快计算速度,节约硬件资源。
FFT 当前最常用方法为 Cooley–Tukey 方法。许多工程计算软件均有 FFT 相关功能,直接导入数据序列进行分析即可。
6 总结
对(1)、(2)文的重点进行总结:
- 傅里叶级数和傅里叶变换表述了连续信号频谱分析方法
- DTFT 表述了无限多样本的离散信号频谱分析方法
- DFT 表述了有限多样本的离散信号频谱分析方法
- 只有 DFT 可直接用于程序计算
- 使用 FFT 可加快 DFT 计算速度
相关文章:
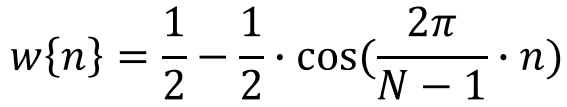
傅里叶分析(2)
在《傅里叶分析(1)》中,讲述了连续信号的傅里叶分析方法,本文讲述离散信号的傅里叶分析方法。 虽然电、声、光、机械振动等信号在物理上是连续函数,但在实际工程中,其通常为离散信号,即若干离散…...

Mysql8数据库如何给用户授权
转载自:https://blog.csdn.net/Numb_ZL/article/details/124222795 查看用户已有权限 SHOW GRANTS FOR [用户名];使用root用户授予所有权限 -- 授权 GRANT ALL PRIVILEGES ON [数据库名].[表明] TO [用户名][连接主机ip地址] WITH GRANT OPTION; -- 刷新权限 FLU…...

reticulate | R-python调用 | 安装及配置 | conda文件配置
reticulate | R-python安装及配置 | conda文件配置 1. 基础知识2. 安装reticulate from CRAN3. 包含了用于Python和R之间协同操作的全套工具,在R和Rstudio中均可使用4. 配置python环境4.1 4种环境配置方式4.2 miniconda 环境install_miniconda()报错一install_minic…...

VueRequest——管理请求状态库
文章目录 前言一、为什么选择 VueRequest?二、使用步骤1.安装2.用例 前言 VueRequest——开发文档 VueReques——GitHub地址 在以往的业务项目中,我们经常会被 loading 状态的管理、请求的节流防抖、接口数据的缓存、分页等重复的功能实现所困扰。每次开…...

GPT-4 Turbo 发布 | 大模型训练的新时代:超算互联网的调度与调优
★OpenAI;ChatGPT;Sam Altman;Assistance API;GPT4 Turbo;DALL-E 3;多模态交互;算力调度;算力调优;大模型训练;GH200;snowflake;AGI;A…...
Django路由层
路由层(urls) Django的路由层是负责将用户请求映射到相应的视图函数的一层。在Django的MVT架构中,路由层负责处理用户的请求,然后将请求交给相应的视图函数进行处理,最后将处理结果返回给用户。 在Django中,…...
关于session的不断变化问题
今天在帮同学解决一个小问题,差点阴沟翻船。 问题再现:他从github上拉了一个项目下来跑,结果发生跑不通问题出现在验证码一直不对。 我一看项目源码,验证码生成后存储再session中了,等用户发送请求验证的时候sessionI…...
eNSP启动路由器一直出#号、以为是安装配置winpcap的问题。。。。(以为是win10安装winpcap失败的问题。。。)
问题描述:eNSP启动一直出#号的一种参考方法_ensp一直#_Hong的博客-CSDN博客 原因是看了这篇博客,觉得ensp启动路由器的时候一直出现#号是因为winpcap安装的时候出现的问题。查看自己的winpcap安装成功之后的目录是: 然后因为那篇…...

时间序列预测:深度学习、机器学习、融合模型、创新模型实战案例(附代码+数据集+原理介绍)
本文介绍->给大家推荐一下我的时间序列预测实战专栏,本专栏平均质量分98分,而且本专栏目前免费阅读。其中涉及机器学习、深度学习、融合模型、个人创新模型、数据分析等一系列有关时间序列的内容,其中的实战案例不仅有简单的模型类似于机器…...
docker安装RocketMQ
1、RocketMQ基本概念 1.1 消息模型(Message Model) RocketMQ主要由Producer、Broker、Consumer三部分组成,其中Producer负责生产消息,Consumer负责消费消息,Broker负责存储消息。Broker在实际部署过程中对应一台服务…...
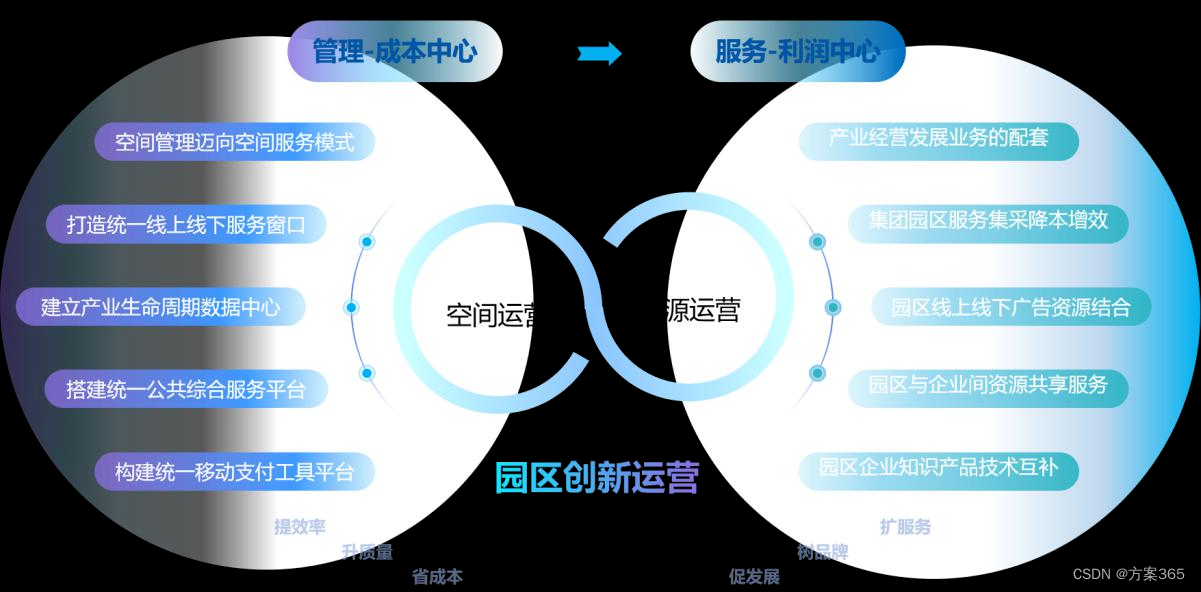
优秀智慧园区案例 - 珠海华发智慧园区,万字长文解析先进智慧园区建设方案经验
一、项目背景 珠海华发产业园运营管理有限公司(简称“产业园公司”)是2016年起连续五年跻身“中国企业500强”、国务院国企改革“双百企业”的珠海华发集团旗下的实体产业发展载体运营平台,依托“四园一基地”:中以国际产业园、信…...

毕业设计项目:基于java+springboot的共享单车信息网站
运行环境 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Ma…...
Redis 连接不上 WRONGPASS invalid username-password pair
1.我的RedisDesktopManager 可以连接 但是 Springboot远程使用Redis就是连不上 2.我的密码是 abc123.. 多了英文的 ..符号 在Springboot过不了,所以Redis密码尽量字母数字,不要其他符号...
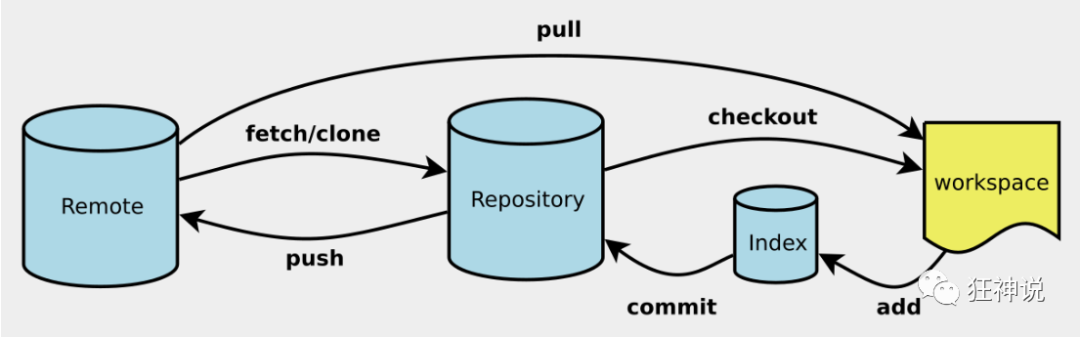
三分钟学完Git版本控制常用指令
基本指令 git clone [url] 克隆远程仓库到本地 git clone https://gitee.com/mayun2023a/mprpc.git2.git checkout -b xxx 切换至新分支xxx(相当于复制了remote的仓库到本地的xxx分支上) 3.修改或者添加本地代码(部署在硬盘的源文件上) 4.g…...

vue3使用粒子特效
安装 //使用npm安装 npm install particles.vue3 --save//使用yarn安装 yarn add particles.vue3 --save//必须得装 npm i tsparticles 使用 main.js import Particles from particles.vue3 const app createApp(App) app.use(Particles)//使用粒子特效 页面使用 <sc…...

DMDEM部署说明-详细步骤-(DM8达梦数据库)
DMDEM部署说明-详细步骤-DM8达梦数据库 环境介绍1 部署DM8 数据库1.1 创建一个数据库作为DEM后台数据库1.2 创建数据库用户 DEM1.3 使用DEM用户导入dem_init.sql 2 配置tomcat2.1 配置/tomcat/conf/server.xml2.2 修改jvm启动参数 3 配置JAVA 1.8及以上版本的运行时环境3.1 配置…...
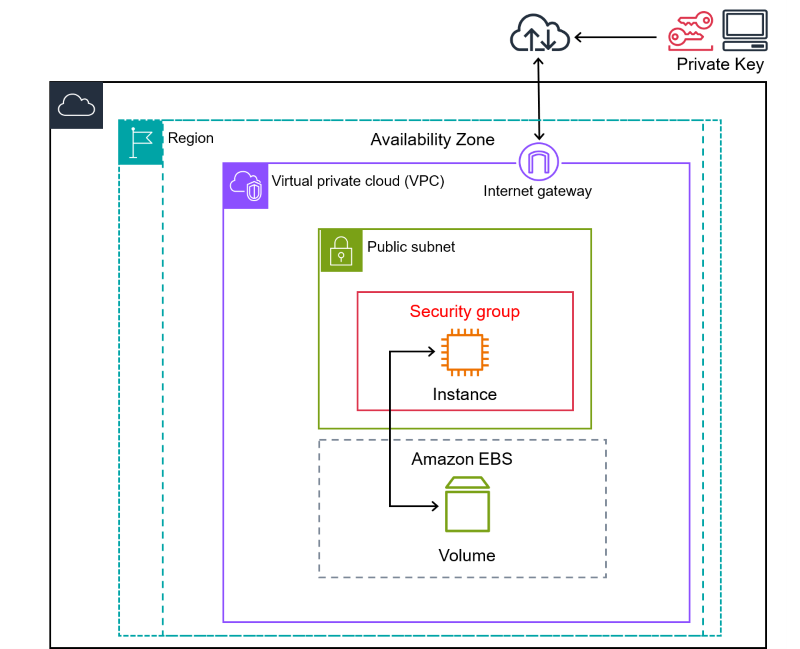
aws亚马逊:什么是 Amazon EC2?
Amazon Elastic Compute Cloud(Amazon EC2)在 Amazon Web Services(AWS)云中按需提供可扩展的计算容量。使用 Amazon EC2 可以降低硬件成本,因此您可以更快地开发和部署应用程序。您可以使用 Amazon EC2 启动所需数量的…...

【BMC】jsnbd介绍
jsnbd介绍 本文主要介绍一个名为jsnbd的开源项目,位于GitHub - openbmc/jsnbd,它实现了一个前端(包含HTML和JS文件)页面,作为存储服务器,可以指定存储内容;还包含一个后端的代理,这…...

个推「数据驱动运营增长」上海专场:携程智行火车票分享OTA行业的智能用户运营实践
近日,以“数据增能,高效提升用户运营价值”为主题的个推「数据驱动运营增长」城市巡回沙龙上海专场圆满举行。携程智行火车票用户运营负责人王银笛分享OTA行业的智能用户运营实践。 ▲ 王银笛 携程智行火车票用户运营负责人 负责智行业务线用户运营。从0…...

Linux--gcc/g++
一、gcc/g是什么 gcc的全称是GNU Compiler Collection,它是一个能够编译多种语言的编译器。最开始gcc是作为C语言的编译器(GNU C Compiler),现在除了c语言,还支持C、java、Pascal等语言。gcc支持多种硬件平台 二、gc…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
