Center Smoothing Certified Robustness for Networks with Structured Outputs
文章目录
- Center Smoothing: Certified Robustness for Networks with Structured Outputs
- Summary
- Research Objective
- Problem Statement
- Methods
- Evaluation
- Conclusion
- Notes
- Gaussian Smoothing
- 常用希腊字母
- 霍夫丁不等式(Hoeffding's inequality)
- 1.简述
- 2.霍夫丁不等式
- 2.1.伯努利随机变量特例
- 2.2.一般形式
Center Smoothing: Certified Robustness for Networks with Structured Outputs
中心平滑:经过认证的具有结构化输出的网络的鲁棒性

Summary
写完笔记之后最后填,概述文章的内容,以后查阅笔记的时候先看这一段。
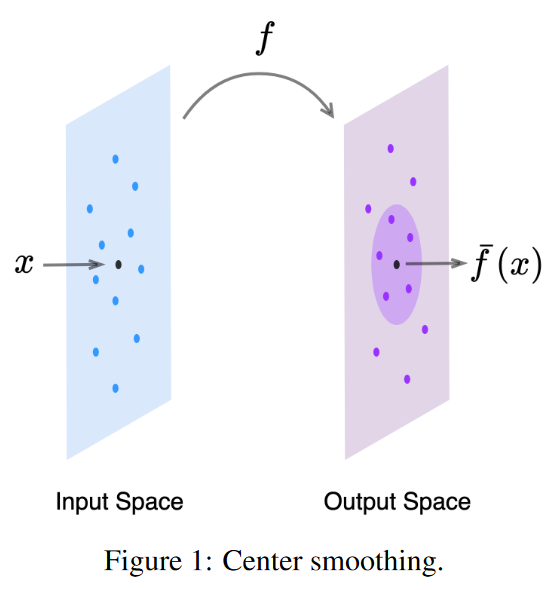
center smooth:对于给定的输入 x x x 与函数 f f f,以及对 x x x 的 l 2 l_2 l2 扰动半径 ϵ 1 \epsilon_1 ϵ1。中心平滑的目的是:在输出空间中计算一个最小半径为 r r r 的包围球,该球的球心为 f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x),这时候的最小包围球包含至少一半的 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))。这时候的 f ˉ \bar{f} fˉ 为 f f f 平滑函数, f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x)为 f ( x ) f(x) f(x)在点 x x x 的平滑输出结果。整个过程如下表示:
∀ x ′ s.t. ∥ x − x ′ ∥ 2 ≤ ϵ 1 , d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ ϵ 2 \forall x^{\prime} \text { s.t. }\left\|x-x^{\prime}\right\|_2 \leq \epsilon_1, d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) \leq \epsilon_2 ∀x′ s.t. ∥x−x′∥2≤ϵ1,d(fˉ(x),fˉ(x′))≤ϵ2
意义在于:给定输入的扰动范围为 ϵ 1 \epsilon_1 ϵ1,经过平滑后的 f ˉ \bar{f} fˉ 能可证明地保证输出变化在 $ \epsilon_2$ 内。解决了 Randomized Smoothing只能局限于具有一维实值输出的分类任务和模型,从而能扩展到可证明的结构化输出(图像、文本、集合)问题。
Research Objective
作者的研究目标。
结构化输出(图像、文本、集合)的可证明鲁棒性
Problem Statement
问题陈述,要解决什么问题?
- 对于图像、文本、集合等结构化输出的问题,可证明的鲁棒性的目标是什么并不是很明显。
- 可证明的对抗鲁棒性研究主要局限于研究具有一维实值输出的分类任务和模型。
Methods
解决问题的方法/算法是什么?
- center smoothing:对于给定的输入 x x x,中心平滑使用高斯平滑分布对 x x x 附近的一组点进行采样,计算每个点上的函数值 f ( x ) f(x) f(x),并返回包含输出中至少一半点的最小球的中心空间。
- 为了优化上述问题,通过计算与样本中所有其他点的中值距离最小的点来近似中心空间的位置。
定义 P \mathcal P P 下 f f f 的平滑版本 f ˉ \bar{f} fˉ 作为在 M M M 中半径最小的球的中心,该球至少包含一半的 f ( x + P ) f (x + \mathcal P) f(x+P) 概率质量:
f ˉ P ( x ) = argmin z r s.t. P [ f ( X ) ∈ B ( z , r ) ] ≥ 1 2 \bar{f}_{\mathcal{P}}(x)=\underset{z}{\operatorname{argmin}} r \text { s.t. } \mathbb{P}[f(X) \in \mathcal{B}(z, r)] \geq \frac{1}{2} fˉP(x)=zargminr s.t. P[f(X)∈B(z,r)]≥21
B ( z , r ) = { z ′ ∣ d ( z , z ′ ) ≤ r } \mathcal{B}(z, r)=\left\{z^{\prime} \mid d\left(z, z^{\prime}\right) \leq r\right\} B(z,r)={z′∣d(z,z′)≤r}
- f ˉ \bar{f} fˉ 为 f f f 的平滑版本, f ( x ) f(x) f(x) 为 M M M中的一个输出元素
- P \mathcal P P 为平滑噪音的分布, δ \delta δ为每一个采样
- z z z 为输出空间 M M M 中的一个元素
- X = x + P X=x+\mathcal P X=x+P代表 x + δ x+\delta x+δ的概率分布,对于输入空间 D \mathcal D D 中的一个元素采样 x x x, 对其进行加平滑噪音
center smooth:
∀ x ′ s.t. ∥ x − x ′ ∥ 2 ≤ ϵ 1 , P [ f ( X ′ ) ∈ B ( f ˉ ( x ) , R ) ] > 1 2 \forall x^{\prime} \text { s.t. }\left\|x-x^{\prime}\right\|_2 \leq \epsilon_1, \mathbb{P}\left[f\left(X^{\prime}\right) \in \mathcal{B}(\bar{f}(x), R)\right]>\frac{1}{2} ∀x′ s.t. ∥x−x′∥2≤ϵ1,P[f(X′)∈B(fˉ(x),R)]>21
d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ 2 R d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) \leq 2 R d(fˉ(x),fˉ(x′))≤2R
d ( f ˉ ( x ) , f ˉ ( x ′ ) ) ≤ d ( f ˉ ( x ) , y ) + d ( y , f ˉ ( x ′ ) ) ≤ R + r ∗ ( x ′ ) \begin{aligned} d\left(\bar{f}(x), \bar{f}\left(x^{\prime}\right)\right) & \leq d(\bar{f}(x), y)+d\left(y, \bar{f}\left(x^{\prime}\right)\right) \\ & \leq R+r^*\left(x^{\prime}\right) \end{aligned} d(fˉ(x),fˉ(x′))≤d(fˉ(x),y)+d(y,fˉ(x′))≤R+r∗(x′)
r ∗ ( x ′ ) ≤ R r^*\left(x^{\prime}\right) \leq R r∗(x′)≤R
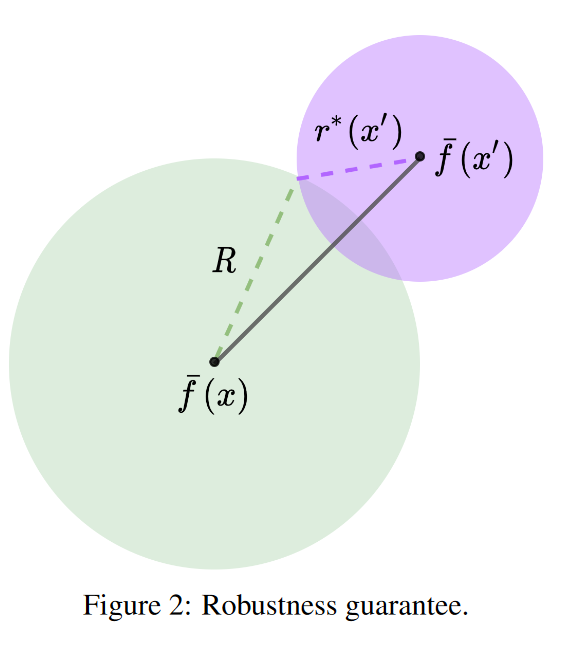
B ( f ˉ ( x ′ ) , r ∗ ( x ′ ) ) \mathcal{B}(\bar{f}(x'),r^*(x')) B(fˉ(x′),r∗(x′)): f ˉ ( x ′ ) \bar{f}(x') fˉ(x′) 为半径最小的球的中心,至少包含 f ( x ′ + P ) f (x' + P) f(x′+P) 概率质量的一半, r ∗ ( x ′ ) r^*(x') r∗(x′) 为最小半径的值
$ \mathcal{B}(\bar{f}(x),R) : : :\bar{f}(x)$ 为球的中心,对于所有满足 ∥ x − x ′ ∥ 2 ≤ ⋅ ϵ 1 \|x-x'\|_2\overset{\cdot}{\leq}\epsilon_1 ∥x−x′∥2≤⋅ϵ1 的 x ′ x′ x′,包含 f ( x ′ + P ) f (x′ + P) f(x′+P) 的概率质量的一半以上, R R R 为球的半径。
上述结果从理论上为我们提供了 f f f 的平滑版本 f ˉ \bar{f} fˉ,具有可证明的鲁棒性保证。因为经过平滑后的 f ˉ ( x ) \bar{f}(x) fˉ(x)与所有 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))的中心距离能够被bound住,因为一个对抗扰动很难去改变 f ( x + N ( 0 , σ c s 2 I ) ) f\left(\boldsymbol{x}+\mathcal{N}\left(0, \sigma_{c s}^2 I\right)\right) f(x+N(0,σcs2I))的中心,所以平滑版本的 f ˉ \bar{f} fˉ能够保证输出的变化的上限。
Evaluation
作者如何评估自己的方法,有没有问题或者可以借鉴的地方。
Conclusion
作者给了哪些strong conclusion, 又给了哪些weak conclusion?
Notes
在这些框架外额外需要记录的笔记。
Gaussian Smoothing
h ˉ ( x ) = argmax c ∈ Y P [ h ( x + δ ) = c ] \bar{h}(x)=\underset{c \in \mathcal{Y}}{\operatorname{argmax}} \mathbb{P}[h(x+\delta)=c] hˉ(x)=c∈YargmaxP[h(x+δ)=c]
p ϵ = Φ ( Φ − 1 ( p ) − ϵ / σ ) p_\epsilon=\Phi\left(\Phi^{-1}(p)-\epsilon / \sigma\right) pϵ=Φ(Φ−1(p)−ϵ/σ)
累计分布函数 Φ \Phi Φ(CDF)是概率分布函数(PDF)的积分。这很好理解。
逆累计分布函数 Φ − 1 \Phi^{-1} Φ−1(ICDF)简单地说,是累计分布函数的反函数。
CDF:已知横轴(某一事件)(值)求纵轴(概率);
ICDF:已知纵轴(概率)求横轴(某一事件)(值);
常用希腊字母
以下是常用希腊字母及其在数学、统计学和科学中的读法:
- α (alpha):常用表示显著性水平,一般读作 “阿尔法”。
- β (beta):常用表示回归系数或错误率,读作 “贝塔”。
- γ (gamma):常用表示形状参数或比率,读作 “伽玛”。
- δ (delta):常用表示误差或变化量,读作 “德尔塔”。
- ε (epsilon):常用表示小量或误差项,读作 “艾普西隆”。
- ζ (zeta):常用表示 Riemann zeta 函数,读作 “泽塔”。
- η (eta):常用表示效应量或预测误差,读作 “艾塔”。
- θ (theta):常用表示角度或参数,读作 “西塔”。
- κ (kappa):常用表示柯西分布或相关系数,读作 “卡帕”。
- λ (lambda):常用表示特征值或密度函数,读作 “兰姆达”。
- μ (mu):常用表示均值或期望值,读作 “缪”。
- ν (nu):常用表示自由度或频率,读作 “纽”。
- ξ (xi):常用表示方差或未知量,读作 “克西”。
- π (pi):常用表示圆周率或概率密度函数,读作 “派”。
- ρ (rho):常用表示相关系数或密度函数,读作 “柔”。
- σ (sigma):常用表示标准差或方差,读作 “西格玛”。
- τ (tau):常用表示 Kendall tau 相关系数或时间常数,读作 “陶”。
- υ (upsilon):常用表示假设检验中的自由度,读作 “宇普西隆”。
- φ (phi):常用表示正态分布的概率密度函数,读作 “斐”。
- χ (chi):常用表示卡方分布,读作 “卡伊”。
- ψ (psi):常用表示角度函数或叶赛尔函数,读作 “普赛”。
- ω (omega):常用表示角频率或参数,读作 “欧米伽”。
霍夫丁不等式(Hoeffding’s inequality)
1.简述
在概率论中,霍夫丁不等式给出了随机变量的和与其期望值偏差的概率上限,该不等式被Wassily Hoeffding于1963年提出并证明。霍夫丁不等式是Azuma-Hoeffding不等式的特例,它比Sergei Bernstein于1923年证明的Bernstein不等式更具一般性。这几个不等式都是McDiarmid不等式的特例。
2.霍夫丁不等式
2.1.伯努利随机变量特例
掷硬币,假设正面朝上概率为 p ,反面朝上概率为 1-p ,投掷 n 次,则正面朝上次数的期望值为 np 。更进一步,有以下不等式:
P ( H ( n ) ≤ k ) = ∑ i = 0 k ( n i ) p i ( 1 − p ) n − i P(H(n) \le k)=\sum_{i=0}^k \binom{n}{i} p^i (1-p)^{n-i}\\ P(H(n)≤k)=i=0∑k(in)pi(1−p)n−i
其中, H(n) 是 n 次投掷中,正面朝上的次数。
对某一 ε > 0 \varepsilon>0 ε>0 ,有 k = ( p − ε ) n k=(p-\varepsilon)n k=(p−ε)n ,上述不等式确定的霍夫丁上界将会按照指数级变化:
P ( H ( n ) ≤ ( p − ε ) n ) ≤ e x p ( − 2 ε 2 n ) ( 2.1.1 ) P(H(n) \le (p-\varepsilon)n) \le exp(-2 \varepsilon^2n) \quad (2.1.1)\\ P(H(n)≤(p−ε)n)≤exp(−2ε2n)(2.1.1)
类似地,可以得到:
P ( H ( n ) ≥ ( p + ε ) n ) ≤ e x p ( − 2 ε 2 n ) ( 2.1.2 ) P(H(n) \ge (p+\varepsilon)n) \le exp(-2 \varepsilon^2n) \quad (2.1.2)\\ P(H(n)≥(p+ε)n)≤exp(−2ε2n)(2.1.2)
综合(2.1.1)(2.1.2),可得:
P ( ( p − ε ) n ≤ H ( n ) ≤ ( p + ε ) n ) ≥ 1 − 2 e x p ( − 2 ε 2 n ) ( 2.1.3 ) P((p-\varepsilon)n\le H(n) \le (p+\varepsilon)n) \ge 1-2exp(-2 \varepsilon^2n) \quad (2.1.3)\\ P((p−ε)n≤H(n)≤(p+ε)n)≥1−2exp(−2ε2n)(2.1.3)
令 ε = ln n / n \varepsilon=\sqrt{\ln{n}/n} ε=lnn/n ,代入(2.1.3),有:
P ( ∣ H ( n ) − p n ∣ ≤ ln n / n ) ≥ 1 − 2 e x p ( − 2 ln n ) = 1 − 2 / n 2 ( 2.1.4 ) P(|H(n)-pn|\le \sqrt{\ln{n}/n})\ge 1-2exp(-2\ln n)=1-2/n^2 \quad (2.1.4) P(∣H(n)−pn∣≤lnn/n)≥1−2exp(−2lnn)=1−2/n2(2.1.4)
(2.1.4)即为霍夫丁不等式的伯努利随机变量特例。
2.2.一般形式
令 X 1 , … , X n X_1,\dots,X_n X1,…,Xn 为独立的随机变量,且 X i ∈ [ a , b ] , i = 1 , … , n X_i\in[a,b] , i=1,\dots,n Xi∈[a,b],i=1,…,n 。这些随机变量的经验均值可表示为:
X ˉ = X 1 + ⋯ + X n n \bar{X}=\frac{X_1+\dots+X_n}{n}\\ Xˉ=nX1+⋯+Xn
霍夫丁不等式叙述如下:
∀ t > 0 , P ( X ˉ − E [ X ˉ ] ≥ t ) ≤ e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.1 ) \forall{t>0},\quad P(\bar{X}-E[\bar{X}]\ge t)\le exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad(2.2.1)\\ ∀t>0,P(Xˉ−E[Xˉ]≥t)≤exp(−∑i=1n(bi−ai)22n2t2)(2.2.1)
令 X ˉ = − X ˉ \bar{X}=-\bar{X} Xˉ=−Xˉ ,代入上述不等式,可得:
∀ t > 0 , P ( E [ X ˉ ] − X ˉ ≥ t ) ≤ e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.2 ) \forall{t>0},\quad P(E[\bar{X}]-\bar{X}\ge t)\le exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.2)\\ ∀t>0,P(E[Xˉ]−Xˉ≥t)≤exp(−∑i=1n(bi−ai)22n2t2)(2.2.2)
综合(2.2.1)(2.2.2),可得霍夫丁不等式的另一种形式:
∀ t > 0 , P ( ∣ X ˉ − E [ X ˉ ] ∣ ≥ t ) ≤ 2 e x p ( − 2 n 2 t 2 ∑ i = 1 n ( b i − a i ) 2 ) ( 2.2.3 ) \forall{t>0},\quad P(|\bar{X}-E[\bar{X}]|\ge t)\le 2exp(-\frac{2n^2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.3)\\ ∀t>0,P(∣Xˉ−E[Xˉ]∣≥t)≤2exp(−∑i=1n(bi−ai)22n2t2)(2.2.3)
若令 S n = X 1 + ⋯ + X n S_n=X_1+\dots+X_n Sn=X1+⋯+Xn ,霍夫丁不等式可叙述为:
$$
\forall{t>0},\quad P(S_n-E[S_n]\ge t)\le exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.4)\
\forall{t>0},\quad P(E[S_n]-S_n\ge t)\le exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.5)\
\forall{t>0},\quad P(|S_n-E[S_n]|\ge t)\le 2exp(-\frac{2t^2}{\begin{matrix} \sum_{i=1}^n (b_i-a_i)^2 \end{matrix}}) \quad (2.2.6)\
$$
从(2.2.1)推导(2.2.4),只需对不等式 X ˉ − E [ X ˉ ] ≥ t \bar{X}-E[\bar{X}]\ge t Xˉ−E[Xˉ]≥t 左右两边同乘系数 n n n ,再令 t = n t t=nt t=nt 即可。不难看出,当 X i X_i Xi 为伯努利随机变量时,(2.2.6)即可转化为(2.1.4)。
需要注意的是, X i X_i Xi 若为无放回抽样时的随机变量,该等式依然成立,尽管此时这些随机变量已不再独立。相关证明可查看Hoeffding在1963年发表的论文。在无放回抽样时,若想要更好的概率边界,可查看Serfling在1974年发表的论文。
学习链接:https://zhuanlan.zhihu.com/p/45342697
随机变量时,(2.2.6)即可转化为(2.1.4)。
需要注意的是, X i X_i Xi 若为无放回抽样时的随机变量,该等式依然成立,尽管此时这些随机变量已不再独立。相关证明可查看Hoeffding在1963年发表的论文。在无放回抽样时,若想要更好的概率边界,可查看Serfling在1974年发表的论文。
学习链接:https://zhuanlan.zhihu.com/p/45342697
相关文章:

Center Smoothing Certified Robustness for Networks with Structured Outputs
文章目录 Center Smoothing: Certified Robustness for Networks with Structured OutputsSummaryResearch ObjectiveProblem StatementMethodsEvaluationConclusionNotesGaussian Smoothing常用希腊字母霍夫丁不等式(Hoeffdings inequality)1.简述2.霍夫…...

C#几种截取字符串的方法
在C#编程中,经常需要对字符串进行截取操作,即从一个长字符串中获取所需的部分信息。本文将介绍几种常用的C#字符串截取方法,并提供相应的示例代码。 目录 1. 使用Substring方法2. 使用Split方法3. 使用Substring和IndexOf方法4. 使用Regex类…...

【PG】PostgreSQL高可用方案repmgr部署(非常详细)
目录 简介 1 概述 1.1 术语 1.2 组件 1.2.1 repmgr 1.2.2 repmgrd 1.3 Repmgr用户与元数据 2 安装部署 2.0 部署环境 2.1 安装要求 2.1.1 操作系统 2.1.2 PostgreSQL 版本 2.1.3 操作系统用户 2.1.4 安装位置 2.1.5 版本要求 2.2 安装 2.2.1 软件包安装 2.2…...

Linux Makefile配置问题
编写一个简单的工程文件,制作Makefile需要包含lpthread,当Makefile写为如下配置时 #CROSSCOMPILE : arm-linux- CROSSCOMPILE :CFLAGS : -Wall -O2 -c CFLAGS -I$(PWD)LDFLAGS : -lpthread LDFLAGS -lm -ldlCC : $(CROSSCOMPILE)gcc #LD :…...

k8s篇之underlay网络和overlay区别
k8s中underlay网络和overlay区别 一、网络 1 Overlay网络: Overlay叫叠加网络也叫覆盖网络,指的是在物理网络的基础之上迭代实现新的虚拟网络,即可使网络中的容器可以互相通信。 优点是对物理网络的兼容性比较好,可以实现pod的…...

掉瓶子小游戏
欢迎来到程序小院 掉瓶子 玩法:旋转的瓶子,根据瓶子方向,点击鼠标左键瓶子掉落,从桌面中间掉下即得1分,卡在桌边瓶子碎了游戏结束,快去掉瓶子吧^^。开始游戏https://www.ormcc.com/play/gameStart/203 htm…...
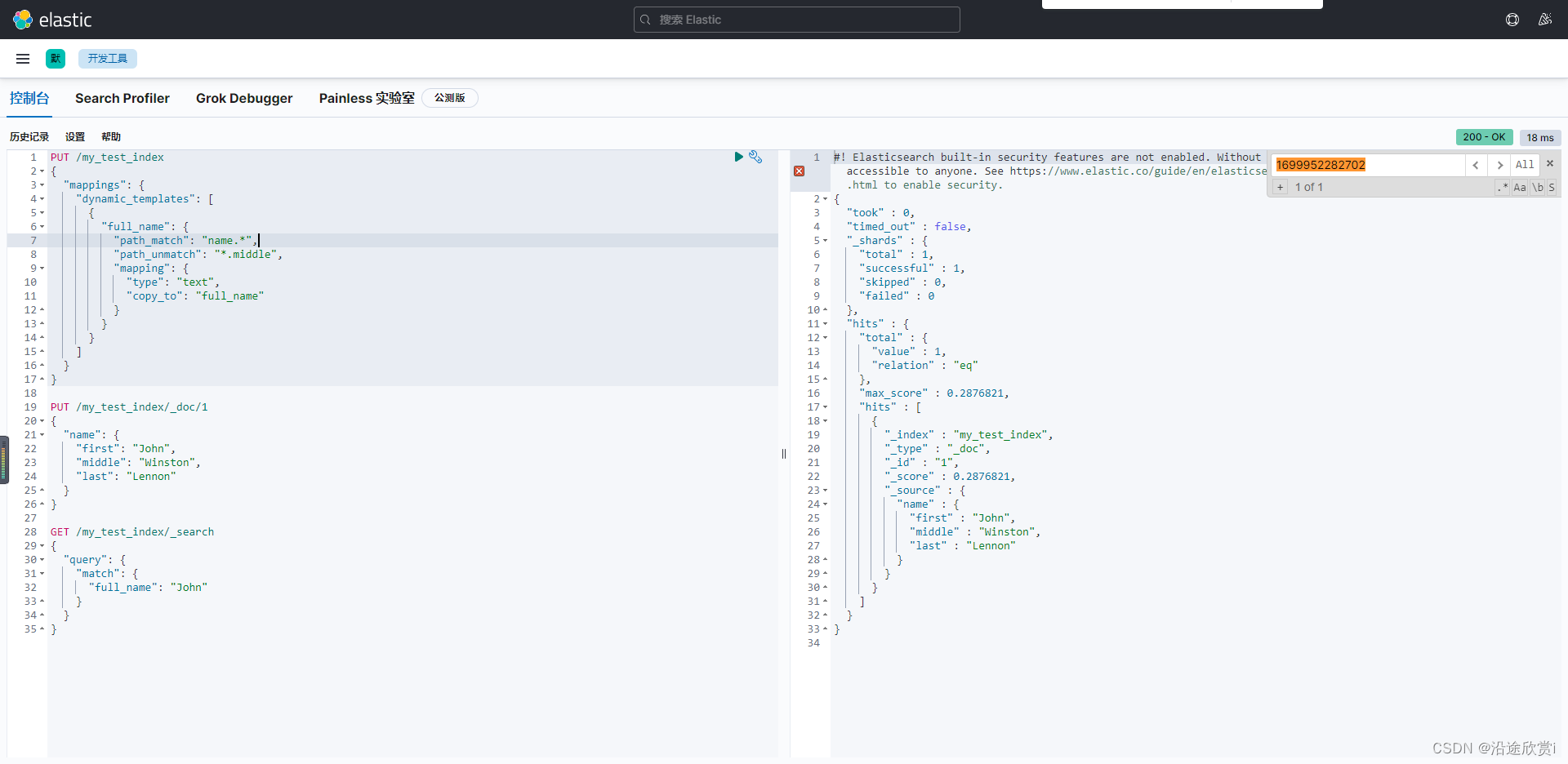
Elasticsearch7 入门 进阶
1、全文检索 1.1、数据分类 按数据分类的话,主要可以分为以下三类: 结构化数据:固定格式、有限长度,比如mysql存的数据非结构化数据:不定长、无固定格式,比如邮件、Word文档、日志等半结构化数据…...

你是怎么封装微信小程序的数据请求的?
当封装微信小程序的数据请求时,可以采用一种模块化的方法,将请求逻辑与界面逻辑分离,以提高代码的可维护性和可扩展性。以下是一个基于前言、高质量代码、理解、优缺点和结尾的范例: 前言 在微信小程序中,数据请求是…...
和size() 的区别)
C++ vector中capacity()和size() 的区别
size是指容器当前拥有元素的个数, capacity是指容器在必须分配新的存储空间之前可以存放的元素总数。 如vector<int> ivect(10),ivect.capacity()10,ivect.size()0, 当向ivect中插入元素时,只要没有超过10个,那么capacity就…...
【Redis】redis-server和redis-cli
上一篇《redis 的下载和安装》 https://blog.csdn.net/m0_67930426/article/details/134341071?spm1001.2014.3001.5501 安装完之后开始使用 打开客户端之前需要先打开服务端 redis-server 直接使用该命令打开就行 然后在打开客户端 redis-cli 使用ping命令查看是否连接服…...

【系统架构设计】架构核心知识: 2.4 系统建模过程和系统设计
目录 一 系统建模过程 1 结构化建模 2 信息工程建模方法 3 面向对象建模方法...
企业电子招标采购系统源码之从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

ubantu libssl.so.1.1: cannot open shared object file
libssl.so.1.1: cannot open shared object file 使用 Ubuntu 22.04 时,有时候会遇到如下错误 error while loading shared libraries: libssl.so.1.1: cannot open shared object file: No such file or directory 这是因为Ubuntu 22.04 默认使用的是 openssl3.0 …...
python matlplotlib/seaborn 绘制曲线的平均值标准差阴影图
1. seaborn 旧版本(0.8.1)中使用tsplot,新版本中使用lineplot 直线代表均值,阴影代表meanstd(带有置信区间,参数ci) import seaborn as sns import matplotlib.pyplot as plt import numpy as np import pandas as p…...
【Linux基础IO篇】深入理解文件系统、动静态库
【Linux基础IO篇】深入理解文件系统、动静态库 目录 【Linux基础IO篇】深入理解文件系统、动静态库再次理解文件系统操作系统内存管理模块(基础)操作系统如何管理内存 Linux中task_struct源码结构 动态库和静态库动静态库介绍:生成静态库库搜…...

flink 写入 starrocks 报错 too many filtered rows attachment
可能原因1 把你starrocks中DDL里的varchar(...) 先修改为STRING. 一般是因为字段超出定义的长度. 可能原因2 csv里有脏数据 导致3列被切分为4列 ....PRIMARY KEY (id) NOT ENFORCED ) WITH (connector starrocks,jdbc-url ...,username ...,password ...,database-nam…...
Windows 安装 Maven
目录 安装 JDK下载 Maven配置阿里云镜像配置环境变量 安装 JDK Windows 安装 JDK 下载 Maven 下载地址:https://maven.apache.org/download.cgi 下载 apache-maven-3.9.5-bin.zip 到本地解压到 D:\Software\apache-maven-3.9.5 配置阿里云镜像 配置阿里云远程仓…...

一文读懂关于IPv6的那些事
作为下一代互联网的战略发展方向,我国正加速IPv6的升级改造,目前从网络基础设施如运营商骨干网、城域网到互联网服务商如各类云服务以及包括手机、电脑、路由器等终端设备厂商都开始支持IPv6网络。那么到底什么是IPv6?IPv6有哪些特点呢&#…...
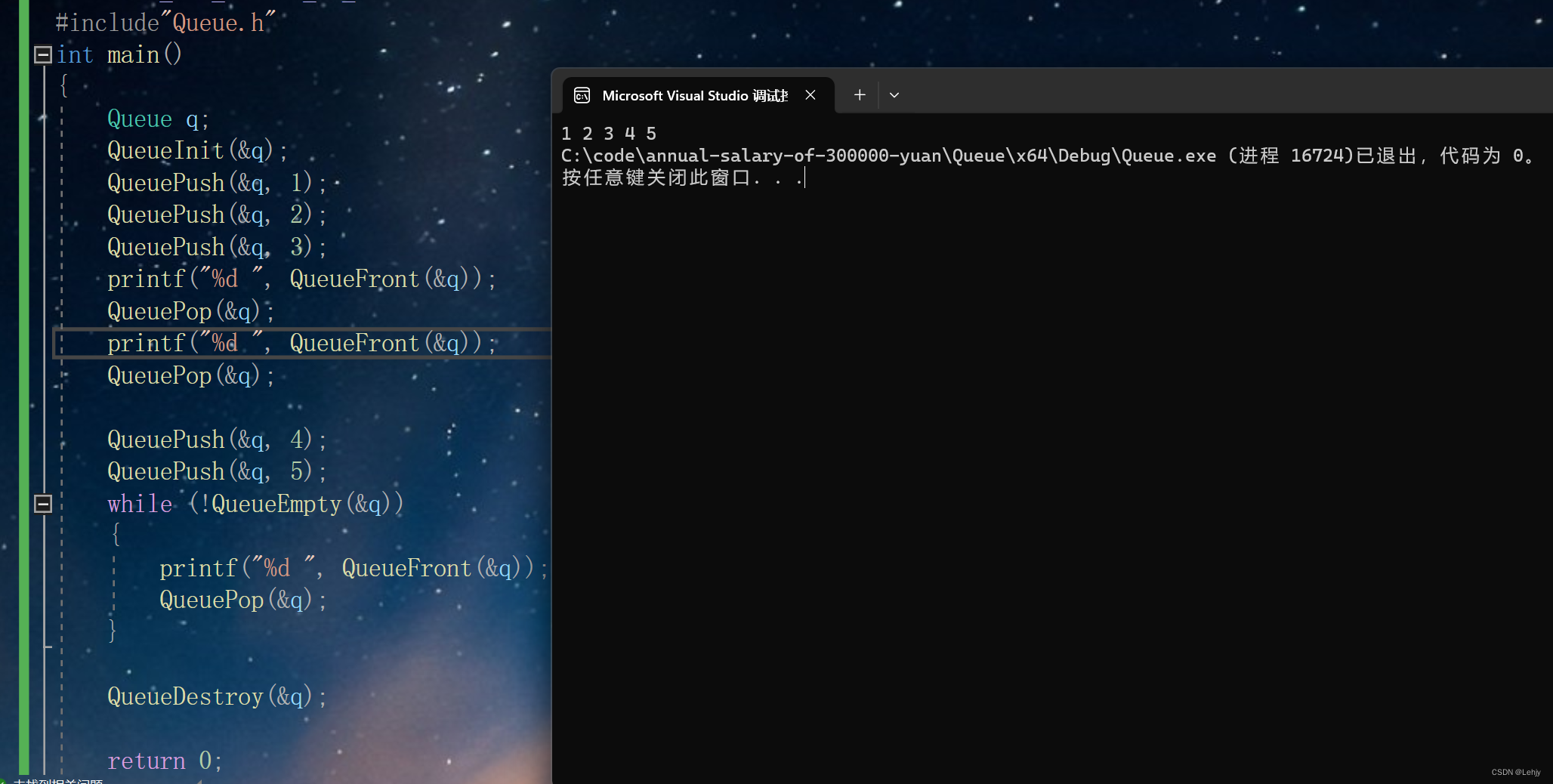
数据结构—队列的实现
前言:上次我们已经学习了数据结构中一个重要的线性表—栈,那么我们这一次就来学习另外一个重要的线性表—队列。 目录: 一、 队列的概念 二、 队列的实现: 1.队列的创建 三、 队列的操作 1.初始化队列 2.队尾入队列 3.队头出队列…...

Linux_shell脚本中的stty
shell脚本中的stty stty是用于配置终端(tty)设置的命令。它允许用户查看和修改与终端相关的各种参数。下面是stty命令的一些常见用法和参数: 基本语法: stty [OPTION] [SETTING]常见选项和参数: 基本设置࿱…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
