js 深度学习(四)
- 函数
var test = function test1(){var a =1,b=2console.log(a,b)test1()//递归
}
console.log(test.name) //test1
test1() //报错
匿名函数表达式 函数自变量
var test = function(){->匿名函数var a =1,b=2console.log(a,b)test1()//递归
}
var test = function(a,b){var a =1,b=2console.log(argyments) //形参
}
function test(a,b)
给未定义的形参赋值还是undefined,给定义的形参赋值可以修改
2、预编译
1.通篇检查语法错误
1.5.预编译的过程
2.解释一行 执行一行
函数声明整体提升,变量只有声明提升,赋值是不提升的
暗示全局变量
var a=1;
b=2;
function test(){var a = b = 1; //函数内部 没有声明 直接赋值存在window
}
函数内部预编译过程
1、寻找形参和变量声明
2、将实参赋值形参
3、寻找函数体声明 赋值函数体
4、执行
相关文章:
)
js 深度学习(四)
函数 var test function test1(){var a 1,b2console.log(a,b)test1()//递归 } console.log(test.name) //test1 test1() //报错匿名函数表达式 函数自变量 var test function(){->匿名函数var a 1,b2console.log(a,b)test1()//递归 }var test function(a,b){var a 1,b2…...
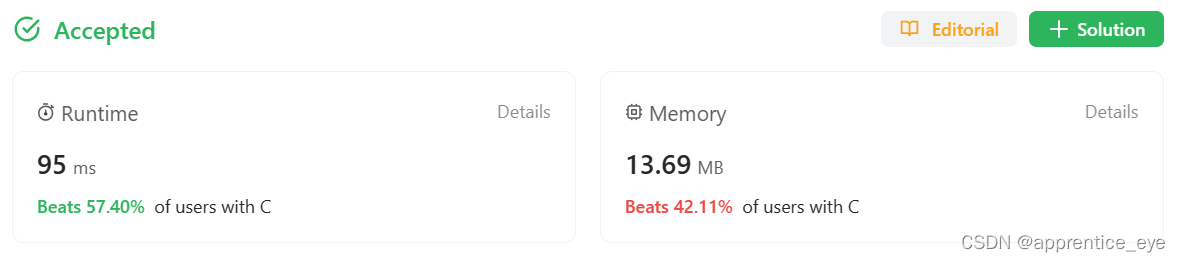
leetcode刷题日记:121. Best Time to Buy and Sell Stock( 买卖股票的最佳时机)
题目给了我们一组数prices,其中prices[i]表示第i天的股票价格,需要我们求出买卖股票所能获得的最大收益。 我们的第一想法就是从算出每一种买卖股票的情况然后求出里面的最大值,这样我们就能得到最大收益是多少,但是这种情况过于复…...
Mac 本地部署thinkphp8【部署环境以及下载thinkphp】
PHP的安装以及环境变量配置 1 PHP安装:在终端输入brew install php 这里是PHP下载的最新的 如果提示‘brew’找不到,自己搜索安装吧, 不是特别难 2 环境变量配置 终端输入vim ~/.bash_profile 输入export PATH"/usr/local/Cellar/php/8.…...
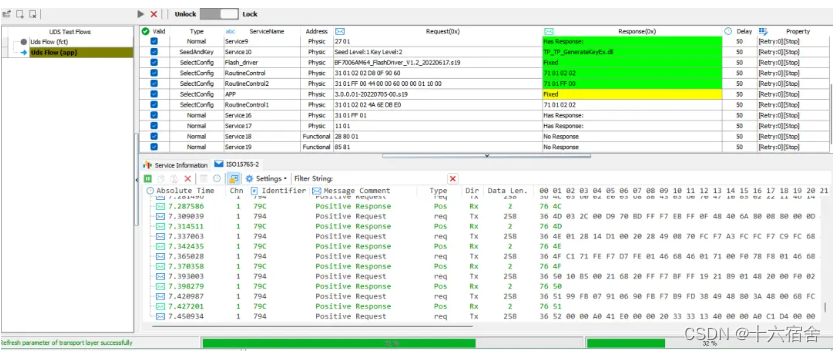
【汽车电子】CAN总线分析仪使用介绍(PCAN/同星CAN卡)
本篇文章以CAN卡的使用为基本线索,介绍了在汽车电子领域涉及的一些CAN卡使用流程,搭配强大的上位机可以实现诸多功能。文章并没有局限于一种CAN卡,而是针对PCAN和同星的CAN卡分别以常用CAN报文收发以及诊断控制台实现这两种方向进行了CAN卡使…...

C //例 7.13 有一个3*4的矩阵,求所有元素中的最大值。
C程序设计 (第四版) 谭浩强 例 7.13 例 7.13 有一个3*4的矩阵,求所有元素中的最大值。 IDE工具:VS2010 Note: 使用不同的IDE工具可能有部分差异。 代码块 方法:使用指针、动态分配内存 #include <stdio.h> …...
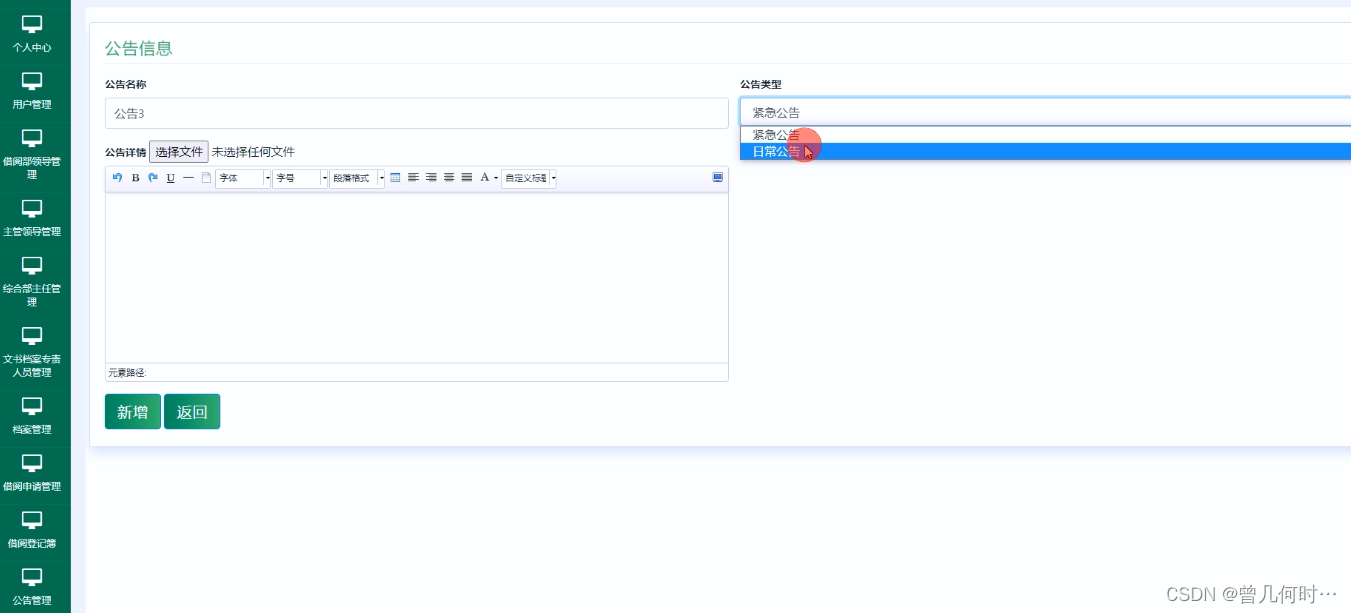
基于SSM的供电所档案管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
excel用RAND函数生成一个大于0小于1的随机数
插入-》函数: 选择RAND函数: 点击“继续”: 点击“确定”,就生成随机数了:...
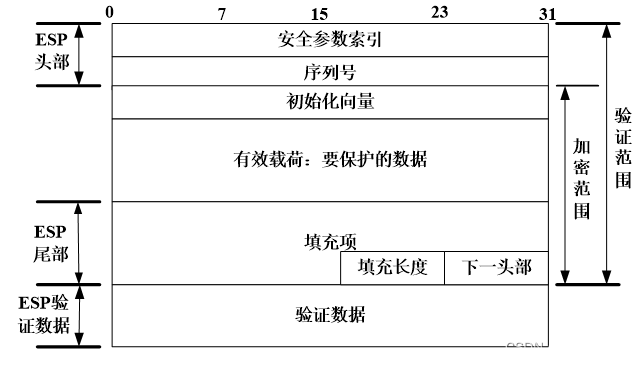
详解IP安全:IPSec协议簇 | AH协议 | ESP协议 | IKE协议
目录 IP安全概述 IPSec协议簇 IPSec的实现方式 AH(Authentication Header,认证头) ESP(Encapsulating Security Payload,封装安全载荷) IKE(Internet Key Exchange,因特网密钥…...

mysql使用--数据库的基本操作
在MYSQL中,一些表的集合称为一个数据库。MYSQL服务器管理若干个数据库,每个数据库下都可有若干个表。 1.展示数据库 SHOW DATABASES; 2.创建数据库 如:CREATE DATABASE myname; 更智能语法,可用:CREATE DATABASE IF …...

计算机毕业设计选题推荐-个人记账理财微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

如何利用IP代理进行海外推广?
在当今数字化的时代,网络营销已经成为企业策略的重要组成部分。而对于进去海外市场的跨境玩家来说,海外的推广推广是重中之重。然而,在开展推广的过程中,我们常常会遇到各种挑战,如地域限制、访问速度慢等。 为了解决…...
流)
使用FFmpeg转封装为hls(m3u8)流
改造ffmpeg/doc/examples/remuxing.c,支持将输入流转封装为hls协议对应的github地址:GitHub - yagerfgcs/FFmpeg at examples/remuxing_support_hls修改点:增加设置hls头 // example:https://www.ffmpeg.org/ffmpeg-all.html#hls-2 // f…...
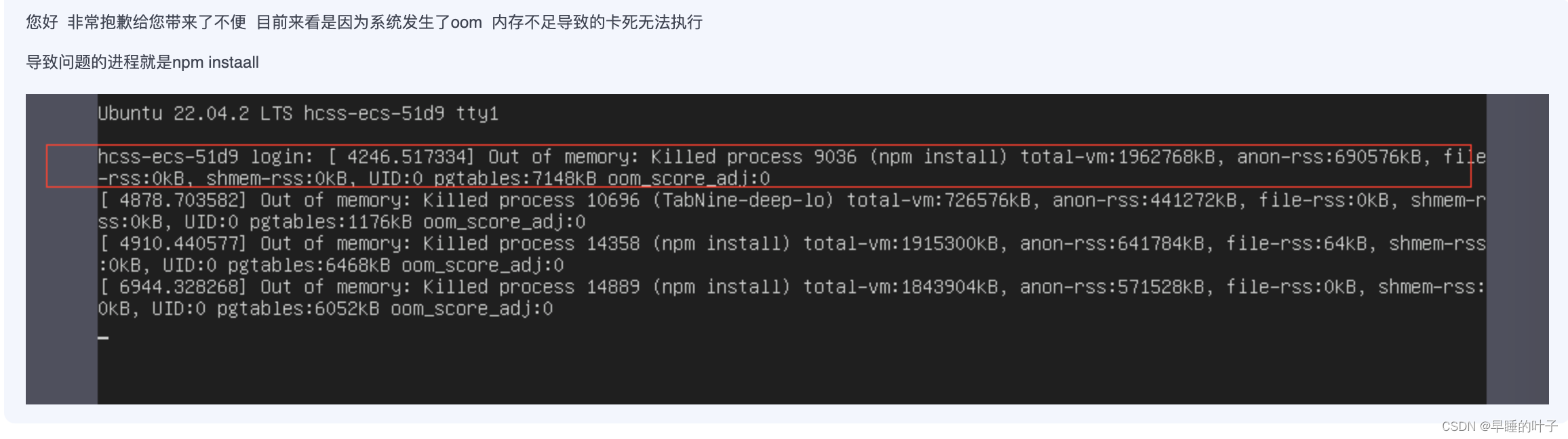
npm install导致的OOM解决方案
文章目录 问题记录解决方法Linux重启排查方法 如何排查Linux自动重启的原因 问题记录 我在华为云服务器配置npm开发环境的时候, SSH远程连接一直掉线,无奈提了工单,被告知是NPM install导致的OOM问题。无语了,破NPM还有这个问题呢…...
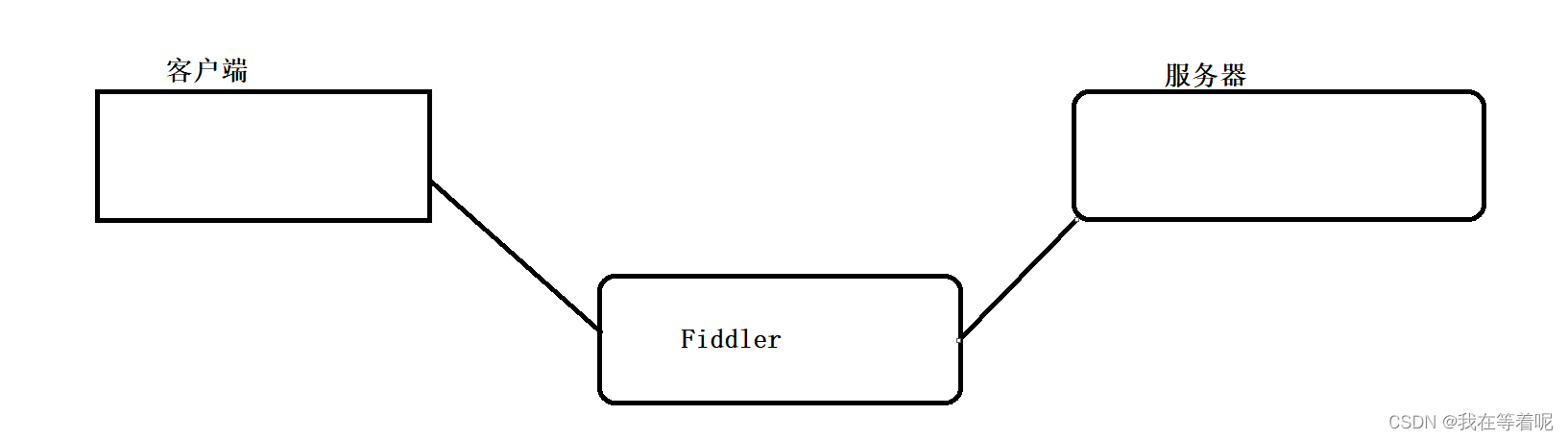
HTTP和HTTPS详解
一)什么是HTTP协议 1)HTTP协议是倾向于相遇业务层次上面的一种协议,传输层协议主要考虑的是端对端之间的一个传输过程,TCP重点进行关注的是可靠传输;咱们的HTTP/1,HTTP/2是基于TCP的,但是咱们的HTTP/3是基于UDP的&…...
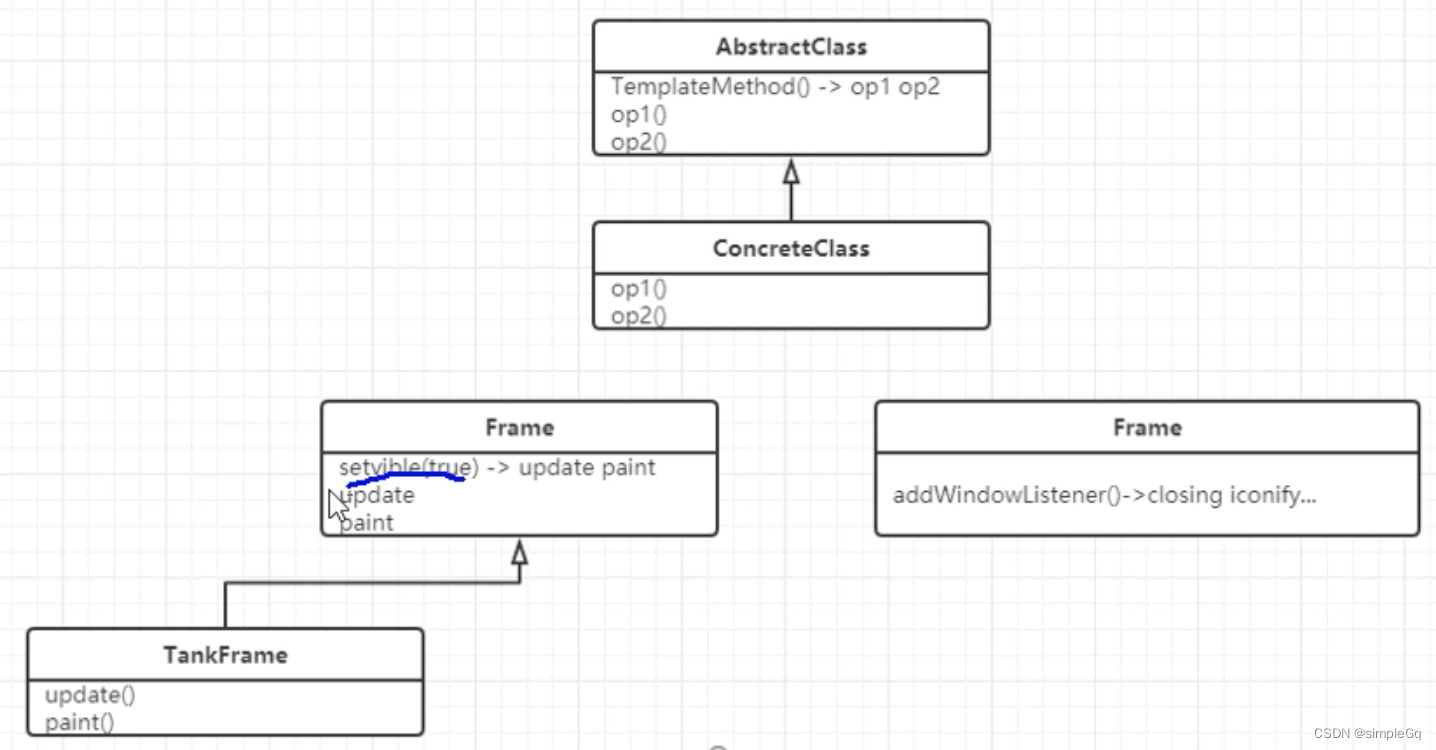
设计模式之模版方法(TemplateMethod)
模版方法 钩子函数 回调函数 在父类里面有一个模版方法,在这个方法里面调用了op1,op2,op3… 在子类里面如果想要改变父类的op1和op2 只需要重写op1和op2,那么这个重写之后的方法,可以在父类里面直接调用的到 例子: J…...

为什么数据安全很重要?哪些措施保护数据安全?
数据安全很重要的原因是因为数据是现代社会的重要财产之一。很多组织和企业依赖数据来做出商业决策,管理客户关系,进行财务规划等等。如果这些数据泄露或遭到黑客攻击,那么就会影响企业的经济利益,甚至影响到个人的隐私和安全。此…...

git push 操作代码回退
git reset revert 回退回滚取消提交返回上一版本 总有一天你会遇到下面的问题. (1)改完代码匆忙提交,上线发现有问题,怎么办? 赶紧回滚. (2)改完代码测试也没有问题,但是上线发现你的修改影响了之前运行正常的代码报错,必须回滚. 这些开发中很常见的问题,所以git的取消提交…...
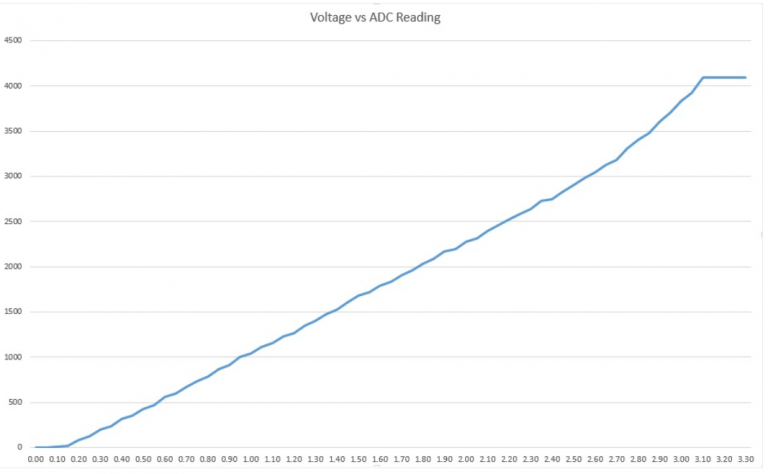
ESP32 Arduino引脚分配参考:您应该使用哪些 GPIO 引脚?
ESP32 芯片有 48 个引脚,具有多种功能。并非所有 ESP32 开发板中的所有引脚都暴露出来,有些引脚无法使用。 关于如何使用 ESP32 GPIO 有很多问题。您应该使用什么引脚?您应该避免在项目中使用哪些引脚?这篇文章旨在成为 ESP32 GP…...

【链接装载与库】 Linux共享库的组织
Linux共享库的组织 由于动态链接的诸多优点,大量的程序开始使用动态链接机制,导致系统里面存在数量 极为庞大的共享对象。如果没有很好的方法将这些共享对象组织起来,整个系统中的共享对象文件则会散落在各个目录下,给长期的维护…...
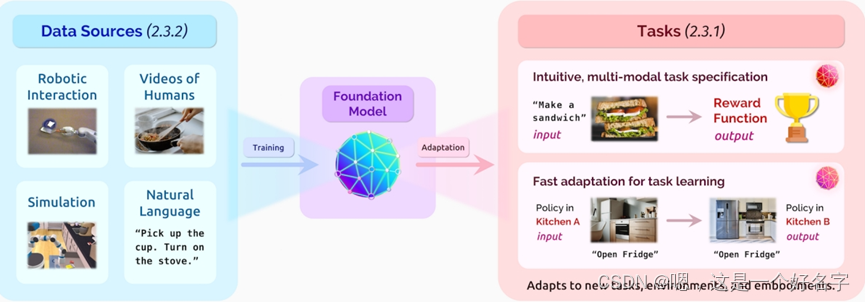
大模型时代的机器人研究
机器人研究的一个长期目标是开发能够在物理上不同的环境中执行无数任务的“多面手”机器人。对语言和视觉领域而言,大量的原始数据可以训练这些模型,而且有虚拟应用程序可用于应用这些模型。与上述两个领域不同,机器人技术由于被锚定在物理世…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
