快乐数[简单]
优质博文:IT-BLOG-CN
一、题目
编写一个算法来判断一个数n是不是快乐数。「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。如果这个过程结果为1,那么这个数就是快乐数。如果n是快乐数就返回true;不是,则返回false。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
1 <= n <= 231 - 1
二、代码
【1】用哈希集合检测循环: 可以先举几个例子。我们从7开始。则下一个数字是49(因为7^2=49),然后下一个数字是97(因为4^2+9^2=97)。我们可以不断重复该的过程,直到我们得到1。因为我们得到了1,我们知道7是一个快乐数,函数应该返回true。再举一个例子,让我们从116开始。通过反复通过平方和计算下一个数字,我们最终得到58,再继续计算之后,我们又回到58。由于我们回到了一个已经计算过的数字,可以知道有一个循环,因此不可能达到1。所以对于116,函数应该返回false。
根据我们的探索,我们猜测会有以下三种可能:
1、最终会得到1。
2、最终会进入循环。
3、值会越来越大,最后接近无穷大。
第三个情况比较难以检测和处理。我们怎么知道它会继续变大,而不是最终得到1呢?我们可以仔细想一想,每一位数的最大数字的下一位数是多少。
| Digits | Largest | Next |
|---|---|---|
| 1 | 9 | 81 |
| 2 | 99 | 162 |
| 3 | 999 | 243 |
| 4 | 9999 | 324 |
| 13 | 9999999999999 | 1053 |
对于3位数的数字,它不可能大于243。这意味着它要么被困在243以下的循环内,要么跌到1。4位或4位以上的数字在每一步都会丢失一位,直到降到3位为止。所以我们知道,最坏的情况下,算法可能会在243以下的所有数字上循环,然后回到它已经到过的一个循环或者回到1。但它不会无限期地进行下去,所以我们排除第三种选择。
即使在代码中你不需要处理第三种情况,你仍然需要理解为什么它永远不会发生,这样你就可以证明为什么你不处理它。
class Solution {public boolean isHappy(int n) {Set<Integer> seen = new HashSet<>();while (n != 1 && !seen.contains(n)) {seen.add(n);n = getNext(n);}return n == 1;}private int getNext(int n) {int totalSum = 0;while (n > 0) {int d = n % 10;n = n / 10;totalSum += d * d;}return totalSum;}
}
时间复杂度: O(243⋅3+logn+loglogn+logloglogn)... = O(logn)。
1、查找给定数字的下一个值的成本为O(logn),因为我们正在处理数字中的每位数字,而数字中的位数由logn给定。
2、要计算出总的时间复杂度,我们需要仔细考虑循环中有多少个数字,它们有多大。
3、我们在上面确定,一旦一个数字低于243,它就不可能回到243以上。因此,我们就可以用243以下最长循环的长度来代替243,不过,因为常数无论如何都无关紧要,所以我们不会担心它。
4、对于高于243的n,我们需要考虑循环中每个数高于243的成本。通过数学运算,我们可以证明在最坏的情况下,这些成本将是O(logn)+O(loglogn)+O(logloglogn)...。幸运的是,O(logn)是占主导地位的部分,而其他部分相比之下都很小(总的来说,它们的总和小于logn,所以我们可以忽略它们。
空间复杂度: O(logn)与时间复杂度密切相关的是衡量我们放入哈希集合中的数字以及它们有多大的指标。对于足够大的n,大部分空间将由n本身占用。我们可以很容易地优化到O(243⋅3)=O(1),方法是只保存集合中小于243的数字,因为对于较高的数字,无论如何都不可能返回到它们。
【2】数学: 根据我们之前的分析,我们知道它必须低于243。因此,我们知道任何循环都必须包含小于243的数字,用这么小的数字,编写一个能找到所有周期的强力程序并不困难。如果这样做,您会发现只有一个循环:4→16→37→58→89→145→42→20→4。所有其他数字都在进入这个循环的链上,或者在进入1的链上。因此,我们可以硬编码一个包含这些数字的散列集,如果我们达到其中一个数字,那么我们就知道在循环中。
class Solution {private static Set<Integer> cycleMembers = new HashSet<>(Arrays.asList(4, 16, 37, 58, 89, 145, 42, 20));public boolean isHappy(int n) {while (n != 1 && !cycleMembers.contains(n)) {n = getNext(n);}return n == 1;}public int getNext(int n) {int totalSum = 0;while (n > 0) {int d = n % 10;n = n / 10;totalSum += d * d;}return totalSum;}
}
时间复杂度: O(logn)。
空间复杂度: O(1),我们没有保留我们所遇到的数字的历史记录。硬编码哈希集的大小是固定的。
【3】快慢指针法: 通过反复调用getNext(n)得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next指针是通过调用getNext(n)函数获得。意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。
我们不是只跟踪链表中的一个值,而是跟踪两个值,称为快跑者和慢跑者。在算法的每一步中,慢速在链表中前进1个节点,快跑者前进2个节点(对getNext(n)函数的嵌套调用)。
1、如果n是一个快乐数,即没有循环,那么快跑者最终会比慢跑者先到达数字1。
2、如果n不是一个快乐的数字,那么最终快跑者和慢跑者将在同一个数字上相遇。
class Solution {public boolean isHappy(int n) {int slowRunner = n;int fastRunner = getNext(n);while (fastRunner != 1 && slowRunner != fastRunner) {slowRunner = getNext(slowRunner);fastRunner = getNext(getNext(fastRunner));}return fastRunner == 1;}public int getNext(int n) {int totalSum = 0;while (n > 0) {int d = n % 10;n = n / 10;totalSum += d * d;}return totalSum;}
}
时间复杂度: O(logn)。该分析建立在对前一种方法的分析的基础上,但是这次我们需要跟踪两个指针而不是一个指针来分析,以及在它们相遇前需要绕着这个循环走多少次。如果没有循环,那么快跑者将先到达1,慢跑者将到达链表中的一半。我们知道最坏的情况下,成本是O(2⋅logn)=O(logn)。一旦两个指针都在循环中,在每个循环中,快跑者将离慢跑者更近一步。一旦快跑者落后慢跑者一步,他们就会在下一步相遇。假设循环中有k个数字。如果他们的起点是相隔k−1的位置(这是他们可以开始的最远的距离),那么快跑者需要k−1步才能到达慢跑者,这对于我们的目的来说也是不变的。因此,主操作仍然在计算起始n的下一个值,即O(logn)。
空间复杂度: O(1),对于这种方法,我们不需要哈希集来检测循环。指针需要常数的额外空间。
相关文章:

快乐数[简单]
优质博文:IT-BLOG-CN 一、题目 编写一个算法来判断一个数n是不是快乐数。「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为1,也可能是无限循环但始终变不到1。如…...

Spring源码阅读-ClassPathXmlApplicationContext
第一步:new一个ClassPathXmlApplicationContext对象 ClassPathXmlApplicationContext xmlContext new ClassPathXmlApplicationContext("mylearn.xml"); 第二步:调用构造方法 public ClassPathXmlApplicationContext(String configLocatio…...

考研分享第2期 | 中央财经大学管理科学跨考北大软微金融科技406分经验分享
一、个人信息 本科院校:中央财经大学 管理科学与工程学院 管理科学专业 上岸院校:北京大学 软件与微电子学院 金融科技专业硕士 考试科目: 初试:思想政治理论 英语一 数学二 经济学综合 面试考察范围广,包括英语自…...

Linux安装java jdk配置环境 方便查询
编辑/etc/profile文件: vim /etc/profile 在文件尾部添加如下配置: export JAVA_HOME/usr/local/jdk1.8.0_161/ export CLASSPATH.: J A V A H O M E / j r e / l i b / r t . j a r : JAVA_HOME/jre/lib/rt.jar: JAVAHOME/jre/lib/rt.jar:JAVA_HOME/l…...

惊群效应之Nginx处理
文章目录 惊群概述Nginx 解决方案之锁的设计锁结构体原子锁创建原子锁获取原子锁实现原子锁释放 Nginx 解决方案之惊群效应总结: 惊群概述 在说nginx前,先来看看什么是“惊群”?简单说来,多线程/多进程(linux下线程进…...

SpringBoot整合Ldap--超详细方法讲解
LADP概述 LDAP(轻量目录访问协议)是一种用于访问和维护分布式目录信息服务的协议。目录服务是一种存储和检索信息的服务,通常用于存储组织内的用户信息、组织结构、网络设备等数据。LDAP是一种轻量级的协议,设计用于在目录中进行查…...

【工程实践】Docker使用记录
前言 服务上线经常需要将服务搬到指定的服务器上,经常需要用到docker,记录工作中使用过dcoker指令。 1.写Dockerfile 1.1 全新镜像 FROM nvidia/cuda:11.7.1-devel-ubuntu22.04ENV WORKDIR/data/Qwen-14B-Chat WORKDIR $WORKDIR ADD . $WORKDIR/RUN ap…...

FreeSwitch安装视频
文章目录 序言Centos7安装FreeSwitch-1.6 序言 学习资料来源《FreeSWITCH权威指南》-作者杜金房这本书。我是2022年6月毕业的,偶然的机会接触到FreeSWITCH,FreeSWITCH纯属个人爱好,进行笔记整理。也一直希望有机会可以参与FreeSWITCH相关工作…...
SpringBoot3+Vue3+Mysql+Element Plus完成数据库存储blob类型图片,前端渲染后端传来的base64类型图片
前言 如果你的前后端分离项目采用SpringBoot3Vue3Element Plus,且在没有OSS(对象存储)的情况下,使用mysql读写图片(可能不限于图片,待测试)。 耗时三天,在踩了无数雷后,…...

攻略 | 参与Moonbeam Ignite Ecosystem Tour
Moonbeam联合Moonwell和Beamswap一起举办社区链上活动,旨在让社区用户通过任务来探索Moonbeam、Moonwell、Beamswap平台。在了解如何使用的同时,参与任务挑战还有机会分得 1700 USDC 奖池 🎁 的奖励!我已经完成全部任务࿰…...
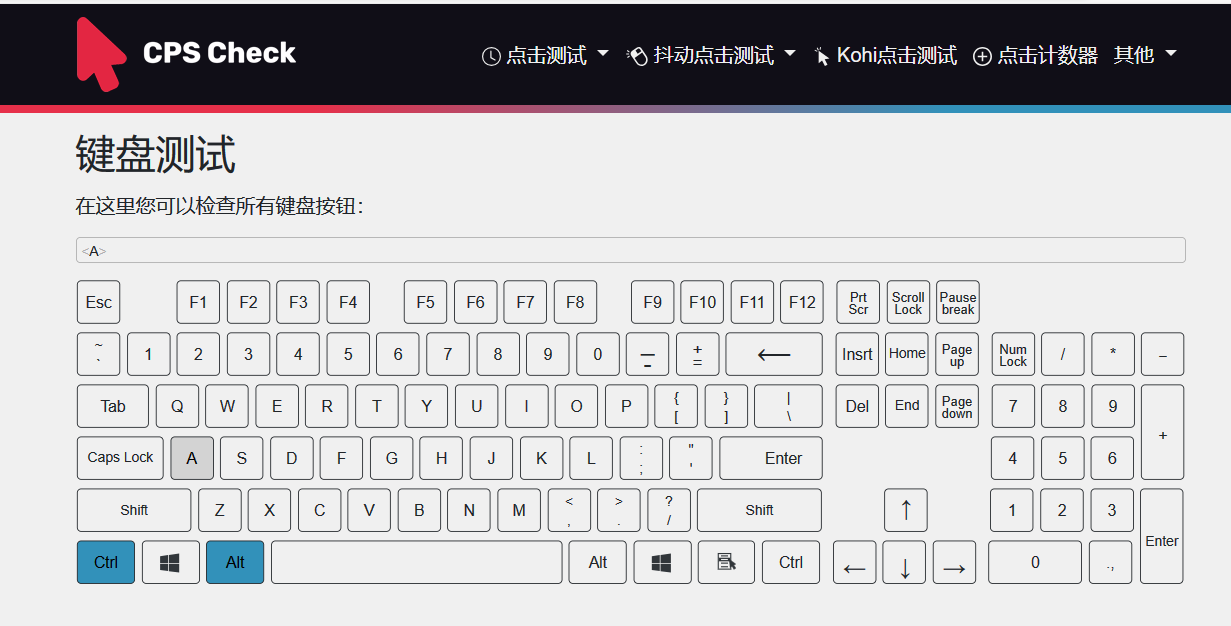
【python自动化】Playwright基础教程(七)Keyboard键盘
【python自动化】Playwright基础教程(七)Keyboard键盘 playwright模拟键盘操作 键盘事件提供了用于管理虚拟键盘的API,高级API是keyboard.type(),它使用的是原始字符再页面上生成对应的keydown 、 keypress / input 和 keyup 事件。 模拟真实键盘操作进行…...

Java读取文件内容写入新文件
要实现读写文件这个过程我们需要导入以下的包 import java.io.BufferedReader; import java.io.BufferedWriter;BufferedReader 用于逐行读取源文件的内容,BufferedWriter 用于逐行写入目标文件。 下面以示例了解如何操作: import java.io.BufferedRe…...

学习samba
文章目录 一、samba介绍二、samba的主要进程三、配置文件四、例子 一、samba介绍 1、SMB(Server Message Block)协议实现文件共享,也称为CIFS(Common Internet File System)。 2、是Windows和类Unix系统之间共享文件的…...

【Ansible】Ansible的Ad-hoc命令执行流程
Ansible的Ad-hoc命令执行流程 用了这么久的Ansible,今天想着研究下Ad-hoc命令的执行流程,从最简单的ping开始吧。 测试命令如下: ansible 172.18.2.31 -m ping先看看回显的结果 [rootbigdata-m-002 etc]# ansible 172.18.2.31 -m ping 17…...

Postgresql 常用整理
文章目录 1. 查询1.1数据库表1.1.1 获取指定数据库表1.1.2 获取指定数据库表所有列名 1.2 别名1.2.1 子表指定别名1.2.2 查询结果指定别名 1.3 临时表1.3.1 定义临时表1.3.2 使用临时表 1.4 子表1.5 分组1.5.1 group by1.5.2 partition by 1.6 分组后合并指定列字段:…...

如何在Jupyter Lab中安装不同的Kernel
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

Java钩子函数的使用
目录 1. Java中常见的钩子函数 2. 使用钩子函数实现程序的清理工作 3. 使用钩子函数处理线程中的未捕获异常 4. 使用钩子函数实现窗口关闭时的操作 在Java编程中,钩子函数(Hook Function)是一种能够在特定事件发生时执行的代码块。钩子函…...
C++跨DLL内存所有权问题探幽(一)DLL提供的全局单例模式
最近在开发的时候,特别是遇到关于跨DLL申请对象、指针、内存等问题的时候遇到了这么一个问题。 问题 跨DLL能不能调用到DLL中提供的单例? 问题比较简单,就是我现在有一个进程A,有DLL B DLL C,这两个DLL都依赖DLL D的…...

短时间不点击云服务器,自动化断开连接,怎么设置长时间
在 Linux 系统中,如果你希望在一段时间内没有操作后保持远程连接不断开,可以通过修改 SSH 服务器的配置来实现。具体的步骤如下: 打开 SSH 服务器的配置文件: sudo vi /etc/ssh/sshd_config 找到以下两个参数并进行修改ÿ…...
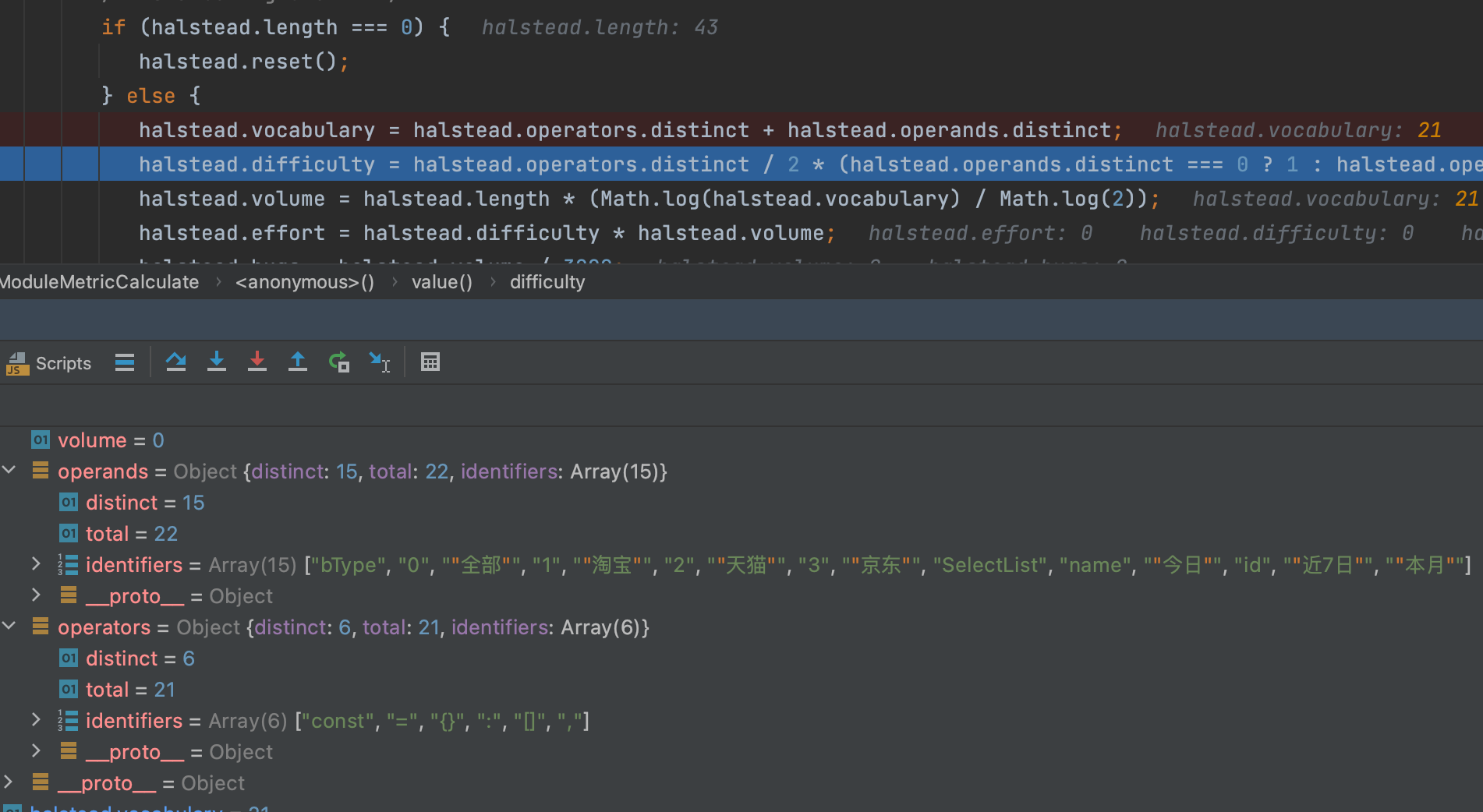
typhonjs-escomplex 代码可读性 可维护度探索
目前市面上的前端代码质量评分中的代码可维护度是大都是基于 typhonjs-escomplex 这个库扫描而来,但是这个库的官方文档并没有介绍相关指标数据的计算规则,不知道规则如何提升指标数据呢?所以本文对 typhonjs-escomplex 源码进行探索…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
