数据结构与算法——3.时间复杂度分析1(概述)
前面我们已经介绍了,研究算法的最终目的是如何花费更少的时间,如何占用更少的内存去完成相同的需求,并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异,但我们并不能将时间占用和空间占用量化。因此,接下来我们要学习有关算法时间耗费和算法空间耗费的描述与分析。有关算法时间耗费分析,我们称之为算法的时间复杂度分析。
1.时间复杂度分析方法
我们要计算算法耗费时间情况,首先我们得度量算法的执行时间,那么如何度量呢?
1.1事后分析估算方法
比较容易想到的方法就是我们把算法执行若干次,然后拿个计时器在旁边计时,这种事后统计的方法看上去的确不错,并且也并非要我们真的拿个计算器在旁边计算,因为计算机都提供了计时的功能。这种统计方法主要是通过设计好的测试程序和测试数据,利用计算机计时器对不同的算法编制的程序的运行时间进行比较,从而确定算法效率的高低,但是这种方法有很大的缺陷︰必须依据算法实现编制好的测试程序,通常要花费大量时间和精力,测试完了如果发现测试的是非常糟糕的算法,那么之前所做的事情就全部白费了,并且不同的测试环境(硬件环境)的差别导致测试的结果差异也很大。
如下例所示:
public static void main(String[] args) {long start = System.currentTimeMillis();int sum = 0;int n = 100;for (int i = 1; i <= n; i++) {sum +=i;}System.out.println("sum="+sum);long end = System.currentTimeMillis();System.out.println(end-start);}如何理解该方法的缺陷?
举例说明:比如我们用来三天的时间写了一个测试某个确定算法的程序,然后运行它,测试这个算法的时间,发现测试时间很长,那在实际中这个算法肯定就不能使用啊,那也就是说这个算法是不好的,是有缺陷不能用的,那么你写的这个测试程序也是不能用的,也就是说你白花了三天时间。这就是一个极大的缺陷。
1.2事前分析估算方法
在计算机程序编写之前,依据统计方法对算法进行估算,经过总结,我们发现一个高级语言编写的程序,程序在计算机上运行消耗的时间取决于下列因素:
- 算法采用的策略和方案;
- 编译产生的代码质量;(不可人为干预)
- 问题的输入规模(所谓的问题输入规模就是输入量是多少);
- 机器执行指令的速度;(不可人为干预)
由此可见,抛开那些与计算机硬件、软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模。如果算法固定,那么该算法的执行时间就只和问题的输入规模有关系了。
2.案例说明
2.1案例一
题目:计算1到100的和
方法一:
//如果输入量n为1,则需要计算1次//如果输入量n为1亿,则需要计算1亿次
public static void main(String[] args) {int sum = 0; //执行1次int n = 100; //执行1次for (int i = 1; i <= n; i++) {//执行n+1次sum +=i; //执行n次}System.out.println("sum="+sum);}方法二:
//如果输入量n为1,则需要计算1次//如果输入量n为1亿,则需要计算1亿次public static void main(String[] args) {int sum = 0; //执行1次int n = 100; //执行1次sum = (n+1)*n/2; //执行1次System.out.println("sum="+sum);}分析:
方法一,当输入规模为n时,方法一执行了1+1+(n+1)+n=2n+3次
方法二,当输入规模为n时,方法二执行了1+1+1=3次
定量具体分析来看,很明显,方法二的执行次数是要远少于方法一的。
下面,我们来深入分析一次这两段代码:
方法一,这个算法求和的核心代码是那个for循环,如果我们把这个for循环看成是一个整体,不考虑什么判断条件啊,什么次数啊,只考虑这个循环里面的内容,然后再忽略其他的一些简要的一次就执行的代码,那么方法一的执行次数就简化为n次
方法二,同样的道理,我们简化那么简单的一次就行的代码语句,重点关注算法的核心语句的执行次数,那么方法二的执行次数就简化为1次
再对比一下,两个方法运行时间的差距就是n与1的差距。
注意:这里我们用了简化思维,直接去抓取每个算法的核心部分,并分析这个核心部分执行的次数
问题:
为什么循环判断条件在方法一中执行了n+1次,看起来是个不小的数字,但是可以忽略呢?
答:看2.2案例二
2.2案例二
题目:计算100个1+100个2+100个3+,,,,,,+100个100的结果
public static void main(String[] args) {int sum = 0;int n = 100;for (int i = 1; i <= n; i++) {for (int j = 1; j <=n ; j++) {sum+=i;}}System.out.println("sum="+sum);}上面这个例子中,如果我们要精确的研究循环的条件执行了多少次,是一件很麻烦的事情,并且,由于真正计算和的代码是内循环的循环体,所以,在研究算法的效率时,我们只考虑核心代码的执行次数,这样可以简化分析。
下面给出2.1中问题的四个答案,可以酌情选择思考
答案1:精确循环次数很麻烦
第一个for循环的条件判断执行了100次,第二个for循环的条件判断执行了10000次,但是请思考下面的几种情况:如果有5层循环,每层次数不一样,让你求第4层循环的判断次数,是不是很麻烦?如果上题中,n=1234,求第二层循环的判断次数是不是也很麻烦?所以,我们忽略循环的判断次数。
答案2:只关心得到结果的最核心部分
上面的所有循环都是为了sum+=i 这句服务的,并且这个算法的最核心部分也是sum+=i,最后的结果也是由这一句得到的,所以,我们只关心这一句。
答案3:当做整体看
因为你每执行一次sum+=i 这句,那就比如执行了前面的for循环的条件判断啊,这二者是一个整体的,是密不可分的,所以就忽略了for的条件判断,只关心那一句
答案4:老师讲的!
我们研究算法复杂度,侧重的是当输入规模不断增大时,算法的增长量的一个抽象(规律),而不是精确地定位需要执行多少次,因为如果是这样的话,我们又得考虑回编译期优化等问题,容易主次跌倒。
我们不关心编写程序所用的语言是什么,也不关心这些程序将跑在什么样的计算机上,我们只关心它所实现的算法。这样,不计那些循环索引的递增和循环终止的条件、变量声明、打印结果等操作,最终在分析程序的运行时间时,最重要的是把程序看做是独立于程序设计语言的算法或一系列步骤。我们分析一个算法的运行时间,最重要的就是把核心操作的次数和输入规模关联起来。
3.函数渐进增长
概念:
给定两个函数f(n)和g(n)如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐近快于(gn)。概念似乎有点艰涩难懂,那接下来我们做几个测试。
3.1测试1
假设四个算法的输入规模都是n :
- 算法A1要做2n+3次操作,可以这么理解︰先执行n次循环,执行完毕后,再有一个n次循环,最后有3次运算
- 算法A2要做2n次操作
- 算法B1要做3n+1次操作,可以这个理解∶先执行n次循环,再执行一个n次循环,再执行一个n次循环,最后有1次运算
- 算法B2要做3n次操作
那么,上述算法,哪一个更快一些呢?
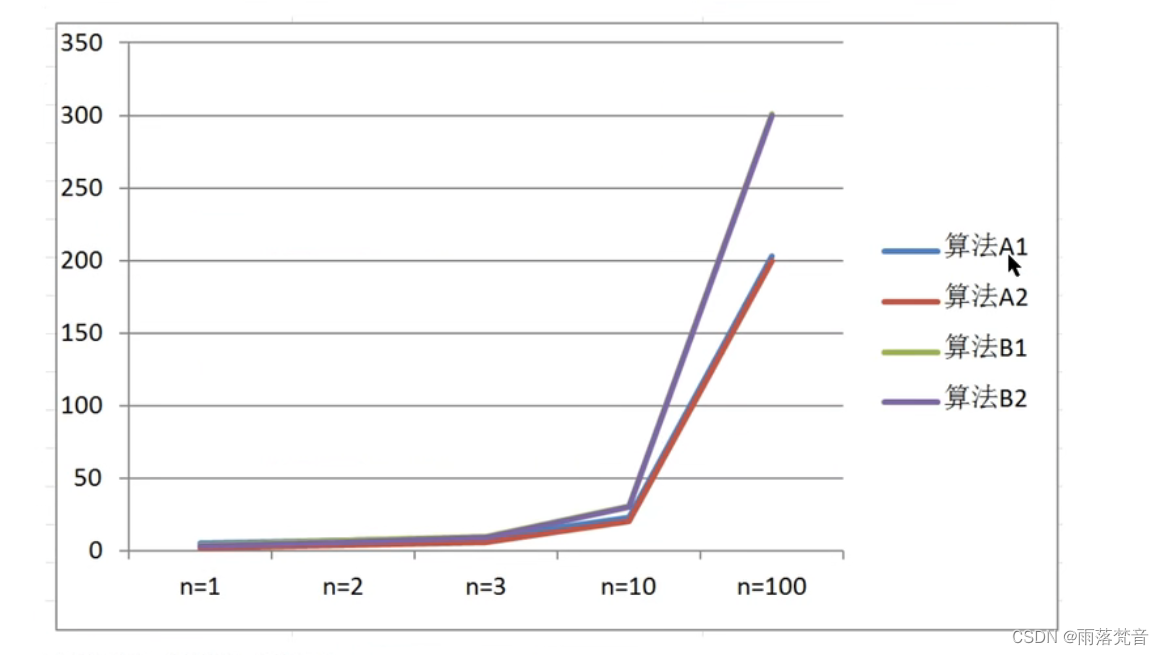
通过数据表格,比较算法A1和算法B1 ∶
- 当输入规模n=1时,A1需要执行5次,B1需要执行4次,所以A1的效率比B1的效率低;
- 当输入规模n=2时,A1需要执行7次,B1需要执行7次,所以A1的效率和B1的效率一样;
- 当输入规模n>2时,A1需要的执行次数一直比B1需要执行的次数少,所以A1的效率比B1的效率高
所以我们可以得出结论︰
当输入规模n>2时,算法A1的渐近增长小于算法B1的渐近增长
通过观察折线图,我们发现,随着输入规模的增大,算法A1和算法A2逐渐重叠到一块,算法B1和
算法B2逐渐重叠到一块,所以我们得出结论︰
随着输入规模的增大,算法的常数操作可以忽略不计
3.2测试2
假设四个算法的输入规模都是n :
- 算法C1需要做4n+8次操作
- 算法C2需要做n次操作
- 算法D1需要做2n^2次操作
- 算法D2需要做n^2次操作
那么上述算法,哪个更快一些?

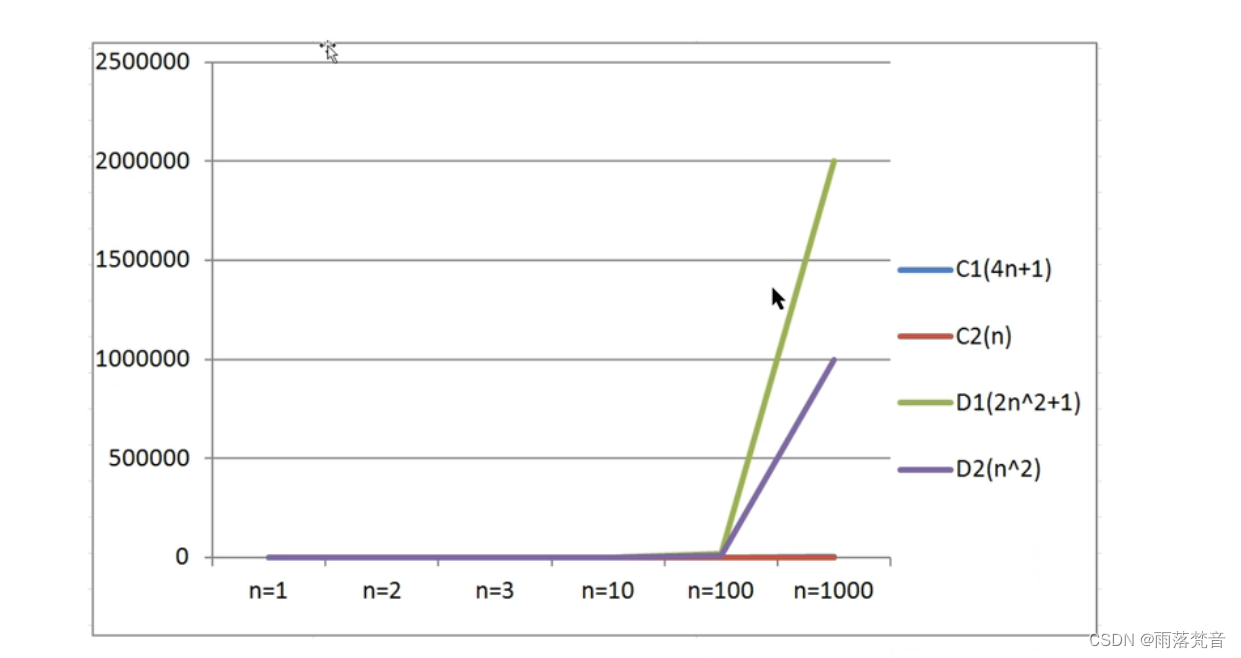
通过数据表格,对比算法C1和算法D1 :
- 当输入规模n<=3时,算法C1执行次数多于算法D1,因此算法C1效率低一些;
- 当输入规模n>3时,算法C1执行次数少于算法D1,因此,算法D2效率低一些,所以,总体上,算法C1要优于算法D1
通过折线图,对比对比算法C1和C2:
随着输入规模的增大,算法C1和算法C2几乎重叠
通过折线图,对比算法C系列和算法D系列:
随着输入规模的增大,即使去除n^2前面的常数因子,D系列的次数要远远高于C系列。
因此,可以得出结论:
随着输入规模的增大,与最高次项相乘的常数可以忽略
3.3测试3
假设四个算法的输入规模都是n:
- 算法E1:2n^2+3n+1;
- 算法E2:n^2
- 算法F1:2n^3+3n+1
- 算法F2:n^3
那么上述算法,哪个更快一些?
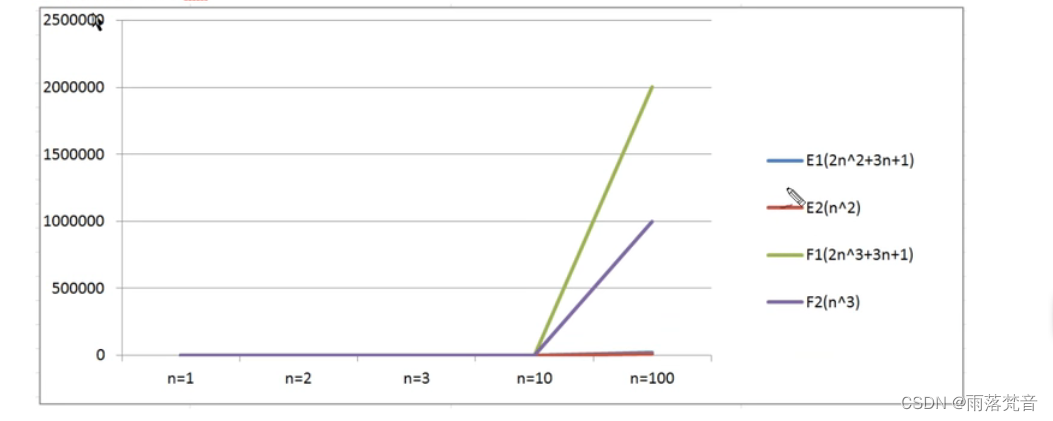 通过数据表格,对比算法E1和算法F1 :
通过数据表格,对比算法E1和算法F1 :
- 当n=1时,算法E1和算法F1的执行次数一样;
- 当n>1时,算法E1的执行次数远远小于算法F1的执行次数;
所以算法E1总体上是由于算法F1的。
通过折线图我们会看到,算法F系列随着n的增长会变得特块,算法E系列随着n的增长相比较算法F
来说,变得比较慢,所以可以得出结论:
最高次项的指数大的,随着n的增长,结果也会变得增长特别快
3.4测试4
假设五个算法的输入规模都是n :
- 算法G :n^3;
- 算法H:n^2;
- 算法I:n;
- 算法J:logn;
- 算法K:1;
那么上述算法,哪个效率更高呢?
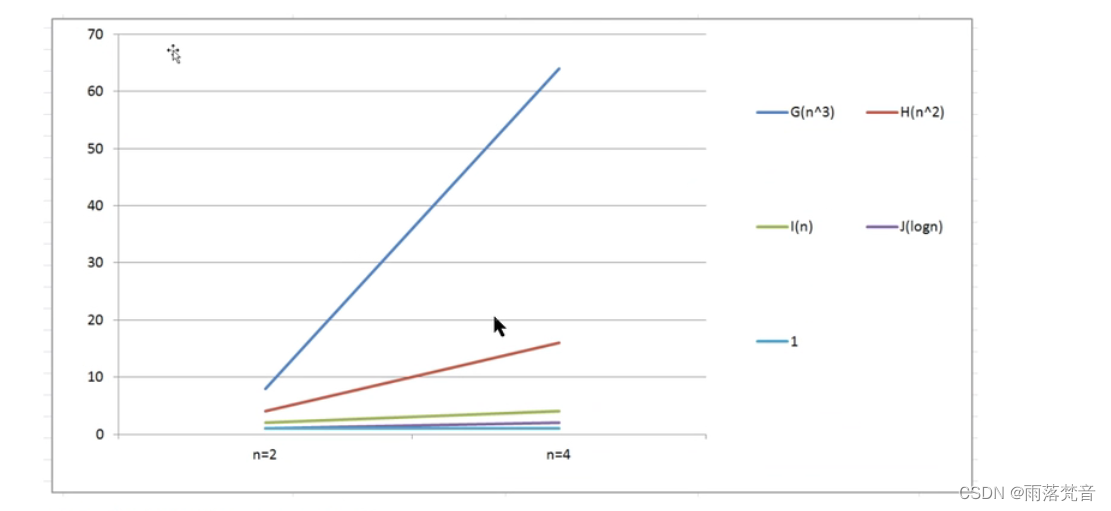
通过观察数据表格和折线图,很容易可以得出结论:
算法函数中n最高次幂越小,算法效率越高
3.5小结
总上所述,在我们比较算法随着输入规模的增长量时,可以有以下规则:
- 算法函数中的常数可以忽略
- 算法函数中最高次幂的常数因子可以忽略
- 算法函数中是高次幂越小,算法效率越高
4.大O计法
4.1具体定义
定义:
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情
况并确定T(n)的量级。算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随
着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简
称时间复杂度,其中f(n)是问题规模n的某个函数。
在这里,我们需要明确一个事情:执行次数=执行时间
用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着输入规模n
的增大,T(n)增长最慢的算法为最优算法。
4.2案例分析
下面用大O表示法来表示一些求和算法的时间复杂度
算法一:
public static void main(String[] args) {int sum = 0;//执行1次int n = 100;//执行1次sum = (n+1)*n/2;//执行1次System.out.println("sum="+sum);}算法二:
public static void main(String[] args) {int sum = 0;//执行1次int n = 100;//执行1次for (int i = 1; i <= n; i++) {sum+=i;//执行n次}System.out.println("sum="+sum);}算法三:
public static void main(String[] args) {int sum = 0;//执行1次int n = 100;//执行1次for (int i = 1; i <= n; i++) {for (int j = 1; j <=n ; j++) {sum+=i;//执行n^2次}}System.out.println("sum="+sum);}如果忽略判断条件的执行次数和输出语句的执行次数,那么当输入规模为n时,以上算法执行的次
数分别为:
算法一:3次
算法二:n+3次
算法三:n^2+2次
如果用大o记法表示上述每个算法的时间复杂度,应该如何表示呢?基于我们对函数渐近增长的分
析,推导大O阶的表示法有以下几个规则可以使用:
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行次数中,只保留高阶项
- 如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数
所以,上述算法的大O计法分别为:
算法一:O(1)
算法二:O(n)
算法三:O(n^2)
5.小结
这篇文章,首先我们给出了算法的时间复杂度的分析方法,引导我们如何去分析一个算法的时间复杂度,然后讲了一系列的函数渐进增长,通过具体的实例总结了一些结论,最后我们在这些结论的基础上提出来大O计法,然后结合大O计法和那些结论,我们实际的分析了一些求和算法的时间复杂度。
相关文章:

数据结构与算法——3.时间复杂度分析1(概述)
前面我们已经介绍了,研究算法的最终目的是如何花费更少的时间,如何占用更少的内存去完成相同的需求,并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异,但我们并不能将时间占用和空间占用量化。因此,接下来…...
FPGA学习之日常工作复位电路
最近一个多月没有写博客了,然后最近工作中也遇到一个复位信号的问题。问题是这样的,关于外部复位信号,之前我们的处理方式都是通过PLL产生的Lock信号作为内部的复位信号。但是由于换到A54上面没有IP核,所以只有不用PLL,…...
)
【洛谷 P1177】【模板】快速排序 题解(快速排序+指针)
【模板】快速排序 题目描述 利用快速排序算法将读入的 NNN 个数从小到大排序后输出。 快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料,掌握后独立完成。(C 选手请不要试图使用 STL,虽然你可以…...
Pthon--自动化实用技巧篇--文件目录处理
为什么要讲这一篇,主要是因为这个在自动化测试框架或者脚本的编写的时候会用到,还是比较方便的。看上述两个函数。getcwd()、chdir()。使用 os.getcwd() 函数获得当前工作目录。使用 os.chdir()函数改变当前工作目录。所以在用chdir()函数的时候别忘记指…...

想招到实干派程序员?你需要这种面试法
技术招聘中最痛的点其实是不精准。技术面试官或CTO们常常会向我们吐槽: “我经常在想,能不能把我们项目中的代码打印出来,作为候选人的面试题的一部分?” “能不能把一个Bug带上环境,让候选人来试试怎么解决…...

cesium常见操作:鼠标点击获取对象
目录 一、viewer.scene.pick(获取Cartesian2) 二、 viewer.scene.pickPosition(获取Cartesian3) 三、viewer.scene.drillPick(穿透拾取,获取所有对象) 四、viewer.scene.globe.pick…...
【玩转c++】git的安装和使用以及可视化处理
本期主题:git的安装和使用(windows环境)博客主页:小峰同学分享小编的在Linux中学习到的知识和遇到的问题 小编的能力有限,出现错误希望大家不吝赐1.两个工具介绍第一个工具git,链接gitee或者github等代码托…...

第三阶段02-Mybatis框架
Mybatis框架 Mybatis框架是目前最流行的数据持久层框架, 使用Mybatis框架可以帮助程序员自动生成JDBC代码, 程序员只需要通过注解或xml配置文件提供需要执行的SQL语句,以及对象和表的映射关系, Mybatis框架会根据此映射关系和SQL自动生成出JDBC代码,从而提高开发效率 Mybatis框…...

基于超像素的多视觉特征图像分割算法研究
0.引言 背景: 经典聚类算法:Kmeans、FCM 现有问题: 1)现有算法大都是基于单一的视觉特征而设计的,eg:基于颜色特征的分割。 2)没有考虑像素周围的空间信息;分割结果:多噪…...

mysql的三大日志
摘自https://blog.csdn.net/chuige2013/article/details/123027580 一. 初步认识 binlog二进制日志 redolog undolog 二. binlog binlog记录写入行操作 作用 1)、主从复制:在Master端开启binlog,然后将binlog发送到各个Slave端,S…...

API接口及社区电子商务化的解释
API是应用程序的开发接口,在开发程序的时候,我们有些功能可能不需要从到到位去研发,我们可以拿现有的开发出来的功能模块来使用,而这个功能模块,就叫做库(libary)。比如说:要实现数据传输的安全,…...

[蓝帽杯 2021]One Pointer PHP
知识点:php 数组整型溢出,open_basedir 绕过分析 利用数组整型溢出绕过,因为PHP 会对溢出的数字处理为 float 类型。 <?php include "user.php"; if($userunserialize($_COOKIE["data"])){$count[$user->count]…...
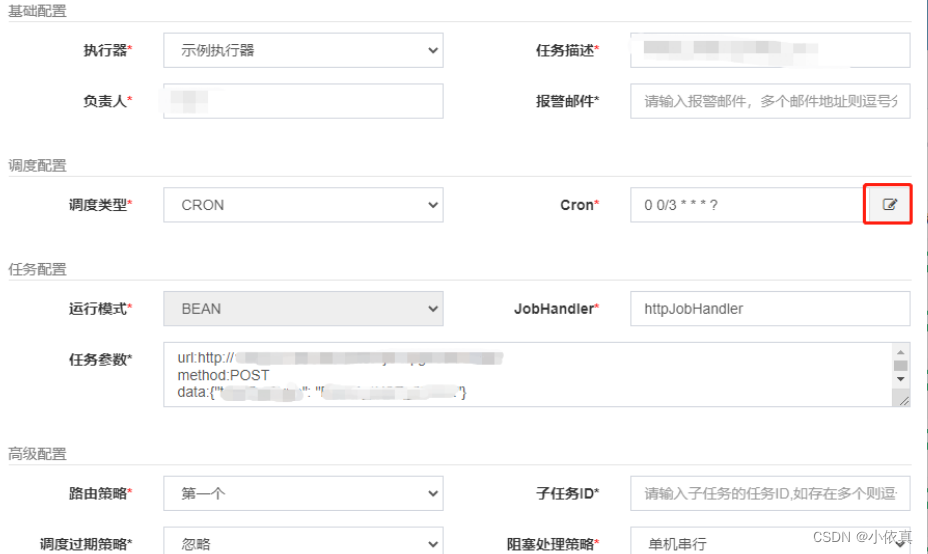
【JAVA】xxl-job服务搭建
xxl-job服务搭建 1.下载xxl-job项目 https://github.com/xuxueli/xxl-job 2.数据库表创建 3.修改配置 注意:这是两个项目,一个是xxl-job前台,一个是xxl-job执行器,找到这两个项目得配置文件,修改配置。 配置文件地址…...

毕业设计 基于STM32单片机生理监控心率脉搏TFT彩屏波形曲线设计
基于STM32单片机生理监控心率脉搏TFT彩屏波形曲线设计1、项目简介1.1 系统构成1.2 系统功能2、部分电路设计2.1 STM32F103C8T6核心系统电路设计2.2心率检测电路设计2.3 TFT2.4寸彩屏电路设计3、部分代码展示3.1 ADC初始化3.2 获取ADC采样值3.3 LCD引脚初始化3.3 在LCD指定位置显…...

【10k~30k的区别】=== 功能测试、自动化测试、性能测试的区别
按测试执行的类型来分:功能测试、自动化测试、性能测试 1.功能测试 功能测试俗称点点点测试。初级测试人员的主要测试任务就是执行测试工程师所写的测试用 例,记录用例的执行状态及bug情况。与开发人员进行交互直到bug被修复。 功能测试理论…...
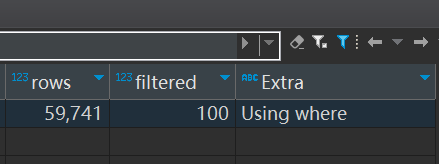
《MySQL学习》 索引失效的三种特殊情况
一.条件字段使用函数 explain select * from bpm_proc_instance bpi where CREATED_AT > 2022-06-01 CREATED_AT 字段建立了索引,此时explain分析的结果表明能使用到索引 但如果我们对 CREATED_AT 字段使用函数 explain select * from bpm_proc_instance bpi w…...
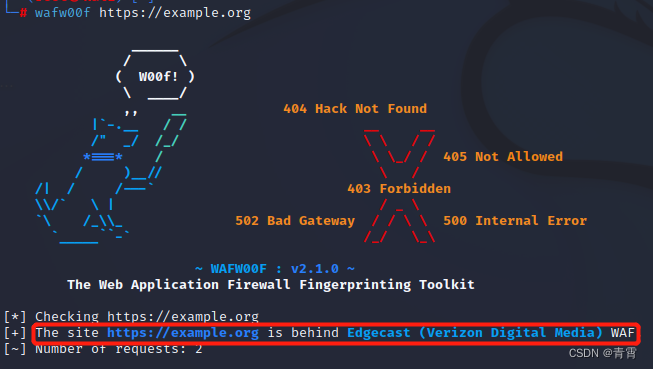
wafw00f 防火墙探测
kali机器自带防火墙探测工具wafw00,它可以通过发送正常以及不正常甚至包含恶意代码的HTTP请求,来探测网站是否存在防火墙,并识别防火墙的厂商及类型。安装:git clone https://github.com/EnableSecurity/wafw00f.git python setup…...
[参考书籍:mysql是怎么运行的])
MySQL学习(1)[参考书籍:mysql是怎么运行的]
目录 一、mysql设计模式和技术 二、mysql服务器和客户端 启动mysql服务 启动mysql客户端程序 三、mysql存储引擎 四、mysql配置 五、mysql系统变量 六、mysql字符集 编码和解码: 常见字符集(五种): 相关概念࿱…...

用Python制作邮件检测器
github地址: https://github.com/CaLlMeErIC/MailDetective 因为需求需要写一个简单的邮件检测系统的框架,这里记录下思路 首先第一反应,这个检测系统不应该是各个邮件收件系统都有自带的吗,于是搜索了下是否有相关的邮件检测开源软件&#…...

K8S---pod基础概念
目录 一、资源限制 二、Pod 的两种使用方式 三、Pod 资源共享 四、底层容器Pause 1、Pause共享资源 1.1 网络 1.2 存储 1.3 小结 2、Pause主要功能 3、Pod 与 Pause 结构的设计初衷 五、Pod容器的分类 1、基础容器(infrastructure container)…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
