DAY54 392.判断子序列 + 115.不同的子序列
392.判断子序列
题目要求:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
- 输入:s = "abc", t = "ahbgdc"
- 输出:true
示例 2:
- 输入:s = "axc", t = "ahbgdc"
- 输出:false
思路
直觉上和昨天的题目很像,判断s是否是t的子序列。
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
确定递推公式:
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:

class Solution {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));for (int i = 1; i <= s.size(); ++i) {for (int j = 1; j <= t.size(); ++j) {if (s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;else dp[i][j] = dp[i][j-1];}}return dp[s.size()][t.size()] == s.size();}
};115.不同的子序列
题目要求:给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。

思路
这道题目如果不是子序列,而是要求连续序列的,那就可以考虑用KMP。
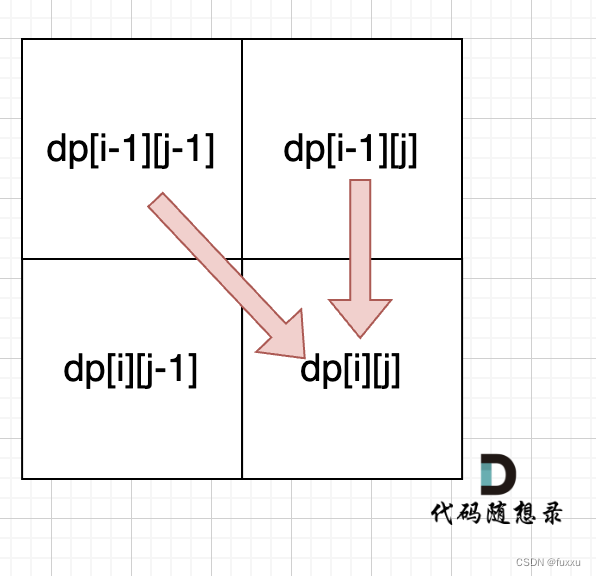
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
这里可能有录友不明白了,为什么还要考虑 不用s[i - 1]来匹配,都相同了指定要匹配啊。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
这里可能有录友还疑惑,为什么只考虑 “不用s[i - 1]来匹配” 这种情况, 不考虑 “不用t[j - 1]来匹配” 的情况呢。
这里大家要明确,我们求的是 s 中有多少个 t,而不是 求t中有多少个s,所以只考虑 s中删除元素的情况,即 不用s[i - 1]来匹配 的情况。
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起,但我为了凸显初始化的逻辑,所以还是加上了。class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));for (int i = 0; i < s.size(); ++i) dp[i][0] = 1;for (int i = 1; i <= s.size(); ++i) {for (int j = 1; j <= t.size(); ++j) {if (s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j] + dp[i-1][j-1];else dp[i][j] = dp[i-1][j];}}return dp[s.size()][t.size()];}
};递归推导过程有点绕,不好理解。而且产生dp的想法很重要,重要的是dp[i][j]代表什么。
- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
相关文章:

DAY54 392.判断子序列 + 115.不同的子序列
392.判断子序列 题目要求:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是…...
【Nginx】nginx | 微信小程序验证域名配置
【Nginx】nginx | 微信小程序验证域名配置 一、说明二、域名管理 一、说明 小程序需要添加头条的功能,内容涉及到富文本内容显示图片资源存储在minio中,域名访问。微信小程序需要验证才能显示。 二、域名管理 服务器是阿里云,用的宝塔管理…...

大数据Doris(二十二):数据查看导入
文章目录 数据查看导入 数据查看导入 Broker load 导入方式由于是异步的,所以用户必须将创建导入的 Label 记录,并且在查看导入命令中使用 Label 来查看导入结果。查看导入命令在所有导入方式中是通用的,具体语法可执行 HELP SHOW LOAD 查看。 show load order by create…...

STM32 I2C详解
STM32 I2C详解 I2C简介 I2C(Inter IC Bus)是由Philips公司开发的一种通用数据总线 两根通信线: SCL(Serial Clock)串行时钟线,使用同步的时序,降低对硬件的依赖,同时同步的时序稳定…...
)
软考 系统架构设计师系列知识点之云计算(1)
所属章节: 第11章. 未来信息综合技术 第6节. 云计算和大数据技术概述 大数据和云计算已成为IT领域的两种主流技术。“数据是重要资产”这一概念已成为大家的共识,众多公司争相分析、挖掘大数据背后的重要财富。同时学术界、产业界和政府都对云计算产生了…...
VS Code画流程图:draw.io插件
文章目录 简介快捷键 简介 Draw.io是著名的流程图绘制软件,开源免费,对标Visio,用过的都说好。而且除了提供常规的桌面软件之外,直接访问draw.io就可以在线使用,堪称百分之百跨平台,便捷性直接拉满。 那么…...
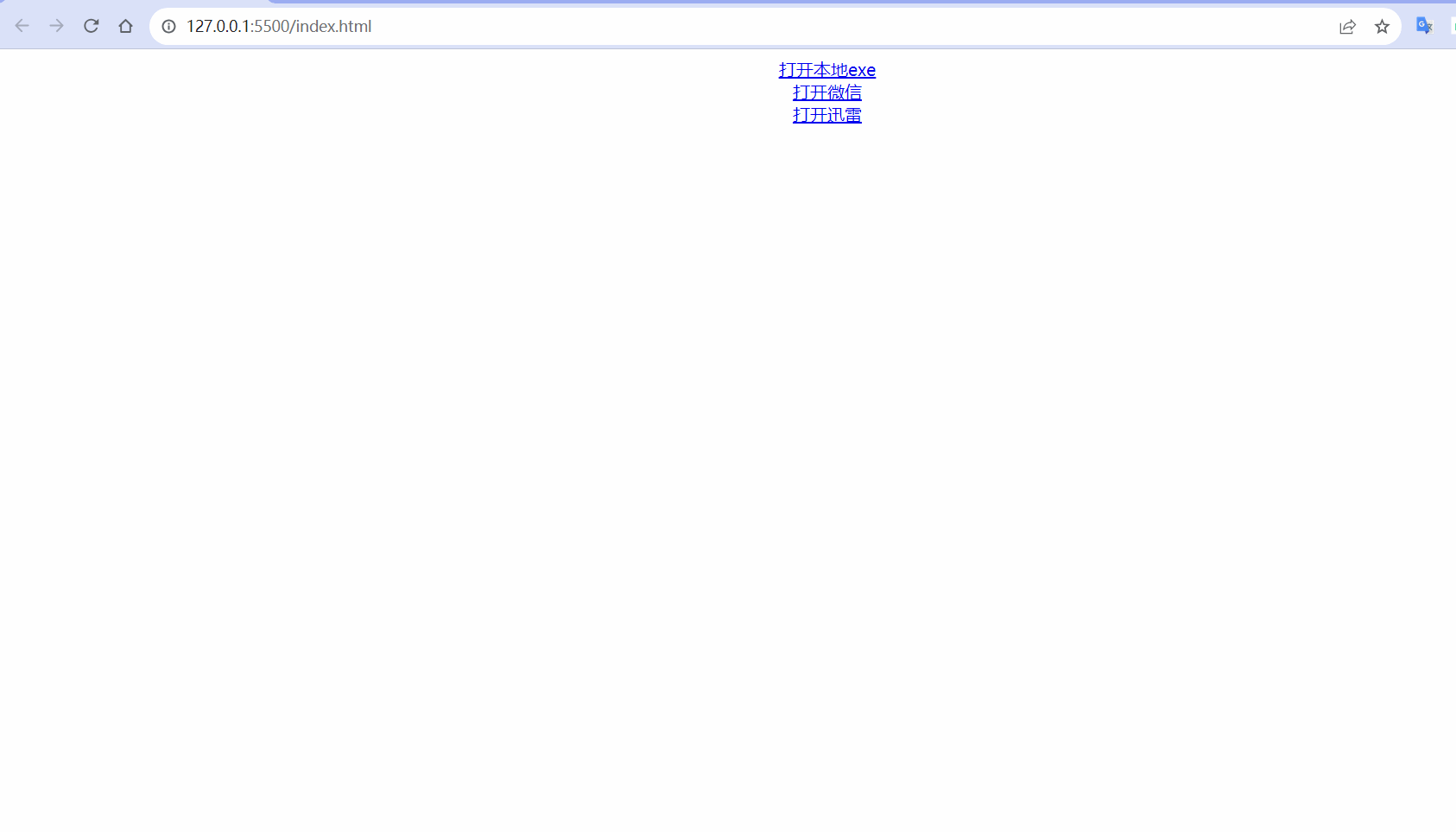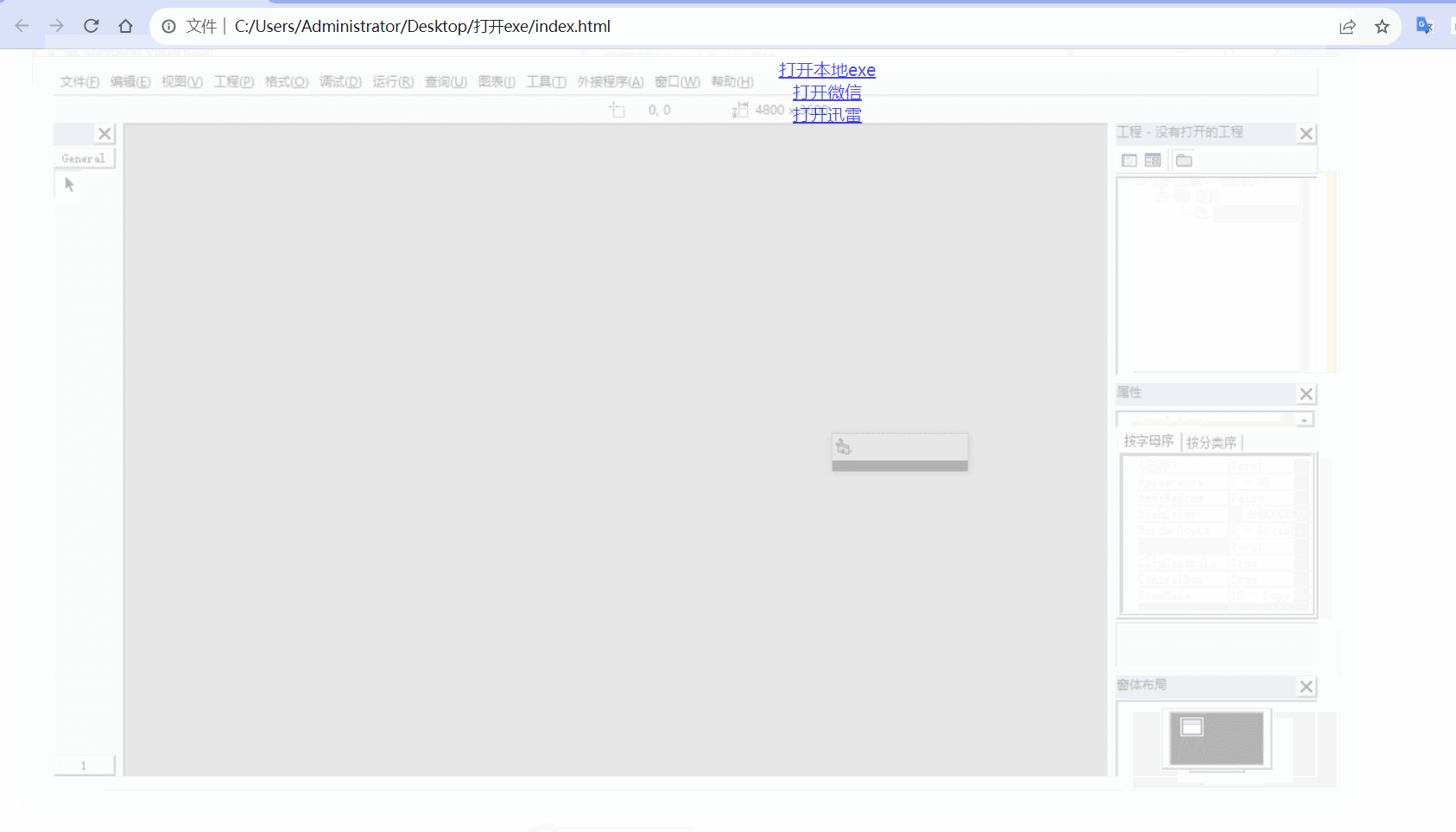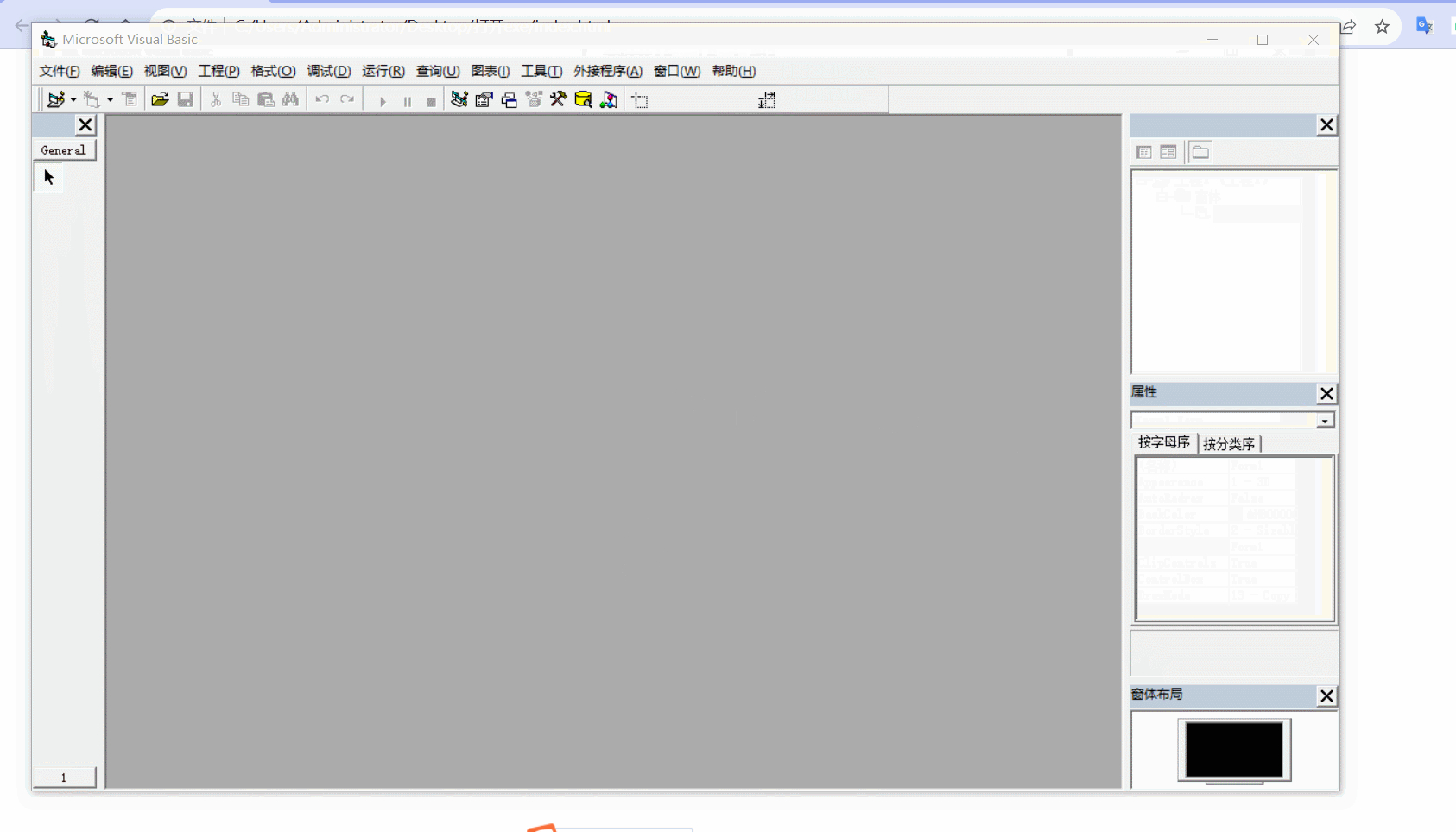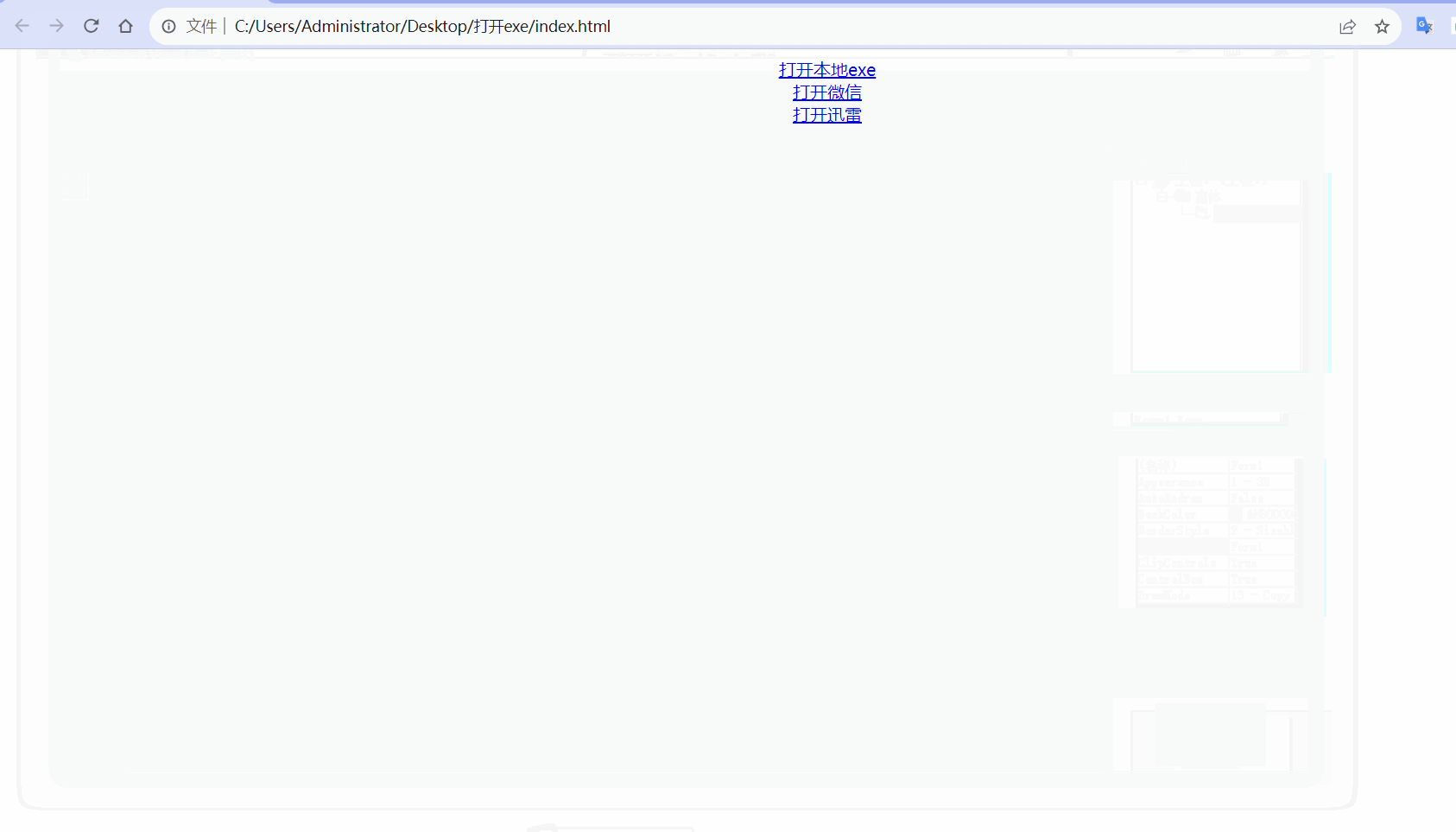
计算机 - - - 浏览器网页打开本地exe程序,网页打开微信,网页打开迅雷
效果 在电脑中安装了微信和迅雷,可以通过在地址栏中输入weixin:打开微信,输入magnet:打开迅雷。 同理:在网页中使用a标签,点击后跳转链接打开weixin:,也会同样打开微信。 运用同样的原理,在网页中点击超…...

C_6练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 下列叙述中正确的是()。 A.C语言程序将从源程序中第一个函数开始执行 B.可以在程序中由用户指定任意一个函数作为…...

XUbuntu22.04之安装pkg-config(一百九十二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

【Proteus仿真】【51单片机】拔河游戏设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用按键、LED、动态数码管模块等。 主要功能: 系统运行后,指示灯处于中间位置,数码管显示得分0,当按下…...
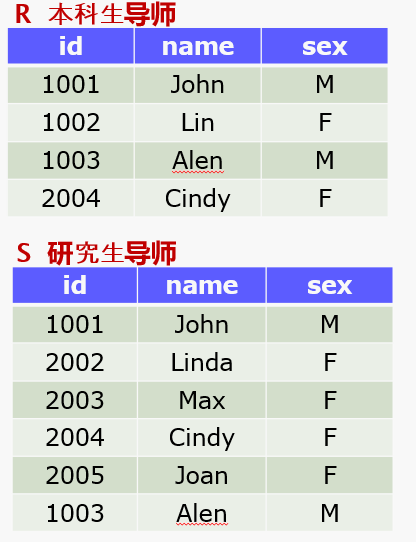
第3关:集合操作100
任务描述相关知识编程要求测试说明 任务描述 本关任务:使用 集合操作解决实际问题 相关知识 1.集合并操作符 可转换为SQL 若R,S的属性名不同,可使用重命名使相应列名一致后进行并操作 例如:R(A,B,C) S(D,E,F) select A,B from R union sel…...

八:ffmpeg命令提取像素格式和PCM数据
一、提取YUV #提取3秒数据,分辨率和源视频一致 fmpeg -i test_1280x720.mp4 -t 3 -pix_fmt yuv420p yuv420p_orig.yuv#提取3秒数据,分辨率转为320x240 ffmpeg -i test_1280x720.mp4 -t 3 -pix_fmt yuv420p -s 320x240 yuv420p_320x240.yuv 二、提取RGB…...
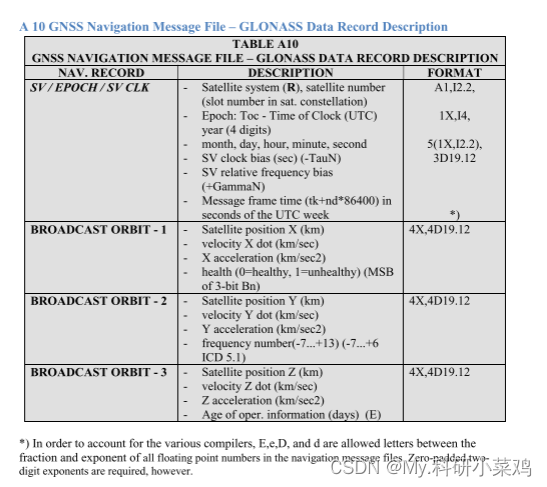
rinex3.04 导航文件
GPS GLA BDS GLO...

linux rsyslog日志采集格式设定二
linux rsyslog日志采集格式设定二 1.创建日志接收模板 打开/etc/rsyslog.conf文件,在GLOBAL DIRECTIVES模块下任意位置添加以下内容 命令: vim /etc/rsyslog.conf 测试:rsyslog.conf文件结尾添加以下内容 $template ztj,"%timegenerated% %hostname% %TIMESTAMP:…...
八股文-面向对象的理解
近年来,IT行业的环境相较以往显得有些严峻,因此一直以来,我都怀有一个愿望,希望能够创建一个分享面试经验的网站。由于个人有些懒惰,也较为喜欢玩乐,导致计划迟迟未能实现。然而,随着年底的临近…...

LeetCode【238】除自身意外的数组的乘积
题目: 思路: https://zhuanlan.zhihu.com/p/109306706?utm_id0 代码: int n nums.length;int[] l new int[nums.length];int[] r new int[nums.length];l[0] 1;r[n-1] 1;for (int i1;i<nums.length;i) {l[i] l[i-1] * nums[i-1]…...

c语言从入门到实战——基于指针的数组与指针数组
基于指针的数组与指针数组 前言1. 数组名的理解2. 使用指针访问数组3. 一维数组传参的本质4. 冒泡排序5. 二级指针6. 指针数组7. 指针数组模拟二维数组 前言 指针的数组是指数组中的元素都是指针类型,它们指向某种数据类型的变量。 1. 数组名的理解 我们在使用指针…...

AUTOSAR汽车电子嵌入式编程精讲300篇-面向车载CAN网络的路由和ECU刷写方法
目录 前言 研究现状 车载CAN的“高层协议”研究现状 车载ECU刷写方法研究现状...
)
软考 系统架构设计师系列知识点之云计算(3)
接前一篇文章:软考 系统架构设计师系列知识点之云计算(2) 所属章节: 第11章. 未来信息综合技术 第6节. 云计算和大数据技术概述 4. 云计算的发展历程 根据云计算的定义和内涵,这里将从虚拟化技术、分布式技术和软件应…...

【万字长文】Python 日志记录器logging 百科全书 之 日志过滤
Python 日志记录器logging 百科全书 之 日志过滤 前言 在Python的logging模块中,日志过滤器(Filter)用于提供更细粒度的日志控制。通过过滤器,我们可以决定哪些日志记录应该被输出,哪些应该被忽略。这对于复杂的应用…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
