LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中:
answer.length == nums.length
answer[i] = |leftSum[i] - rightSum[i]|
其中:
leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不存在对应的元素,leftSum[i] = 0 。
rightSum[i] 是数组 nums 中下标 i 右侧元素之和。如果不存在对应的元素,rightSum[i] = 0 。
返回数组 answer 。
示例 1:
输入:nums = [10,4,8,3]
输出:[15,1,11,22]
解释:数组 leftSum 为 [0,10,14,22] 且数组 rightSum 为 [15,11,3,0] 。
数组 answer 为 [|0 - 15|,|10 - 11|,|14 - 3|,|22 - 0|] = [15,1,11,22] 。
解法一:先计算出leftSum和rightSum,然后模拟即可:
class Solution {
public:vector<int> leftRigthDifference(vector<int>& nums) {int sz = nums.size();vector<int> leftSum(sz);leftSum[0] = 0;for (int i = 1; i < sz; ++i) {leftSum[i] = nums[i - 1] + leftSum[i - 1];}vector<int> rightSum(sz);rightSum[sz - 1] = 0;for (int i = sz - 2; i >= 0; --i) {rightSum[i] = nums[i + 1] + rightSum[i + 1];}vector<int> ans(sz);for (int i = 0; i < sz; ++i) {ans[i] = abs(leftSum[i] - rightSum[i]);}return ans;}
};
如果输入数组大小为n,此算法时间复杂度为O(n),空间复杂度为O(n)。
解法二:可以边遍历边计算leftSum和rightSum的当前和,从而减少空间复杂度:
class Solution {
public:vector<int> leftRigthDifference(vector<int>& nums) {int rightSum = accumulate(nums.begin(), nums.end(), 0);int leftSum = 0;int sz = nums.size();vector<int> ans(sz);for (int i = 0; i < sz; ++i) {rightSum -= nums[i];ans[i] = abs(leftSum - rightSum);leftSum += nums[i];}return ans;}
};
如果输入数组大小为n,此算法时间复杂度为O(n),空间复杂度为O(1)。
相关文章:

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

rollup环境配置
VUE2.x源码学习笔记 1. rollup环境配置 首先在VScode中新建文件夹vue_sc,然后终端打开定位到打开的文件夹,输入“npm init -y”初始化配置项,运行成功之后文件夹新增package.json文件 继续在终端运行"npm install babel/preset-env ba…...

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
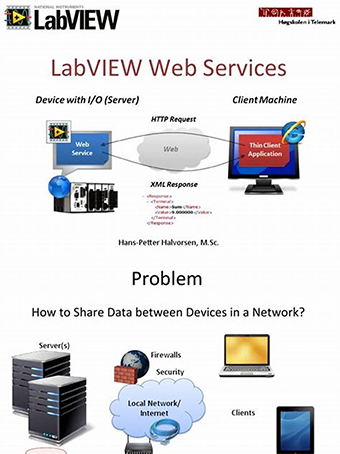
LabVIEW网络服务安全2
LabVIEW网络服务安全2在客户端应用程序中创建签名对请求进行签名要求您具有能够从客户端的编程语言调用的MD5摘要算法以及SHA256加密摘要算法的实现。这两种算法通常都可用于大多数平台。还需要:1. 要使用的HTTP方法的字符串(“GET”、“POST”、“PUT”…...
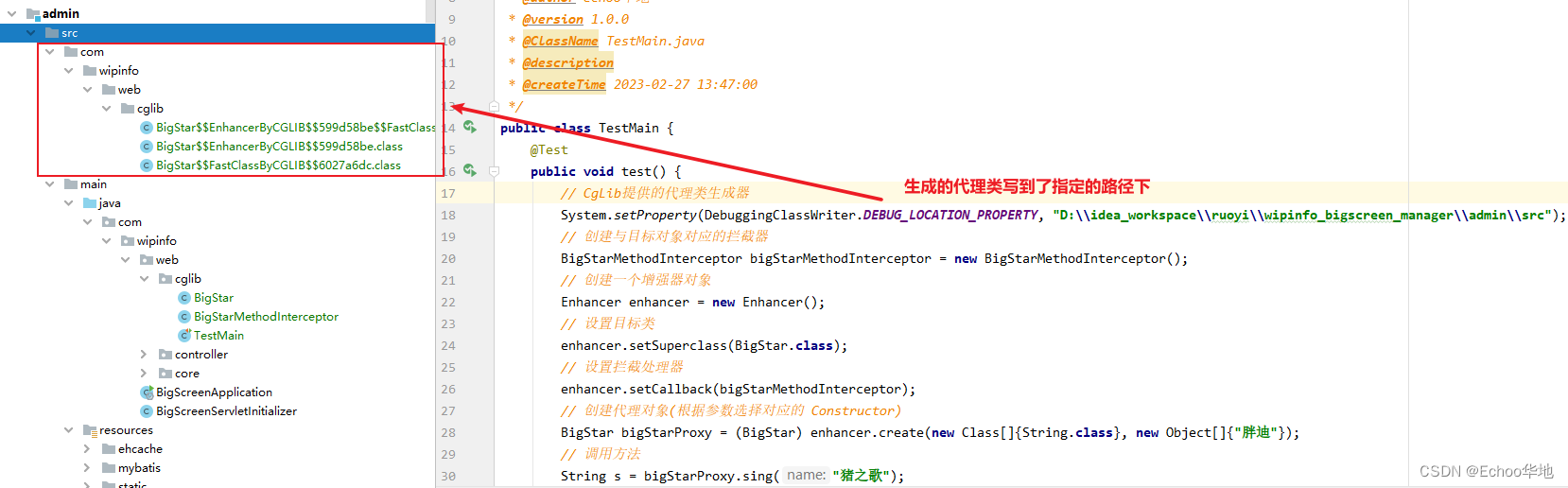
java动态代理
目录儿一、代理模式的作用二、实现代理的方式三、动态代理的实现3.1 jdk动态代理3.2 cglib动态代理一、代理模式的作用 功能增强: 基于某个功能,再增加一些功能。 (比如目标类只负责核心功能,其他附属功能通过代理类完成。代理类的方法名与目…...
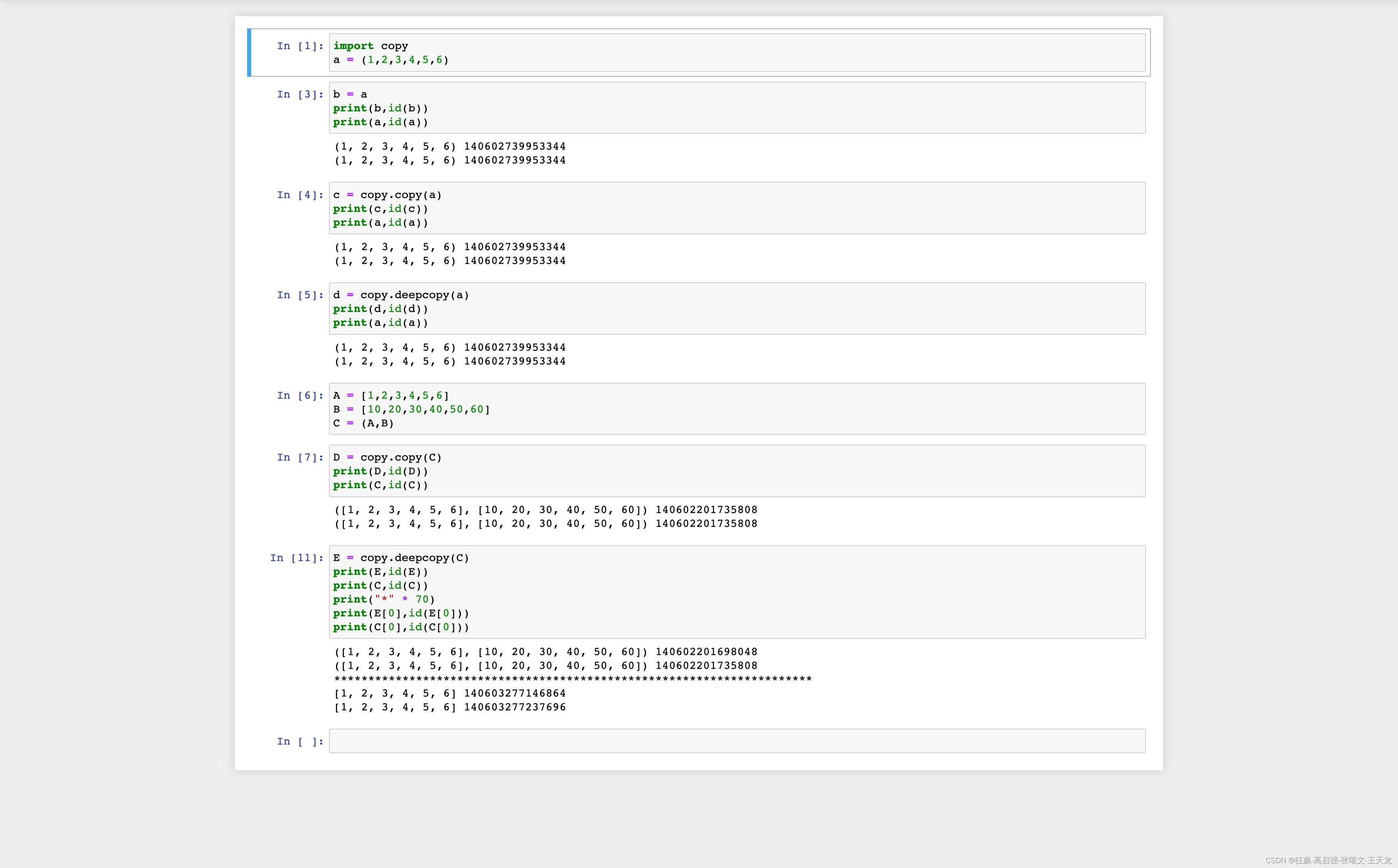
Python 简单可变、复杂可变、简单不可变、复杂不可变类型的copy、deepcopy的行为
copy模块:copy:浅拷贝deepcopy:深拷贝简单可变类型、复杂可变的copy()、deepcopy():简单不可变、复杂不可变类型的copy()、deepcopy():结论:对于简单类型的可变类型copy是深拷贝,改变了该拷贝变…...
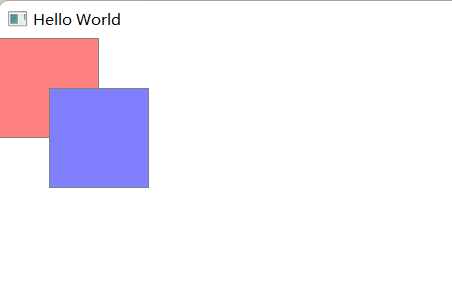
QML Item
在QML中所有的可视项目都继承自Item,虽然Item本身没有可视化的外观,但它定义了可视化项目的所有属性。 Item可以作为容器使用: Item{Rectangle{id:retc}Rectangle{id:retc1}Rectangle{id:retc2}Rectangle{id:retc3}} item拥有children属性…...
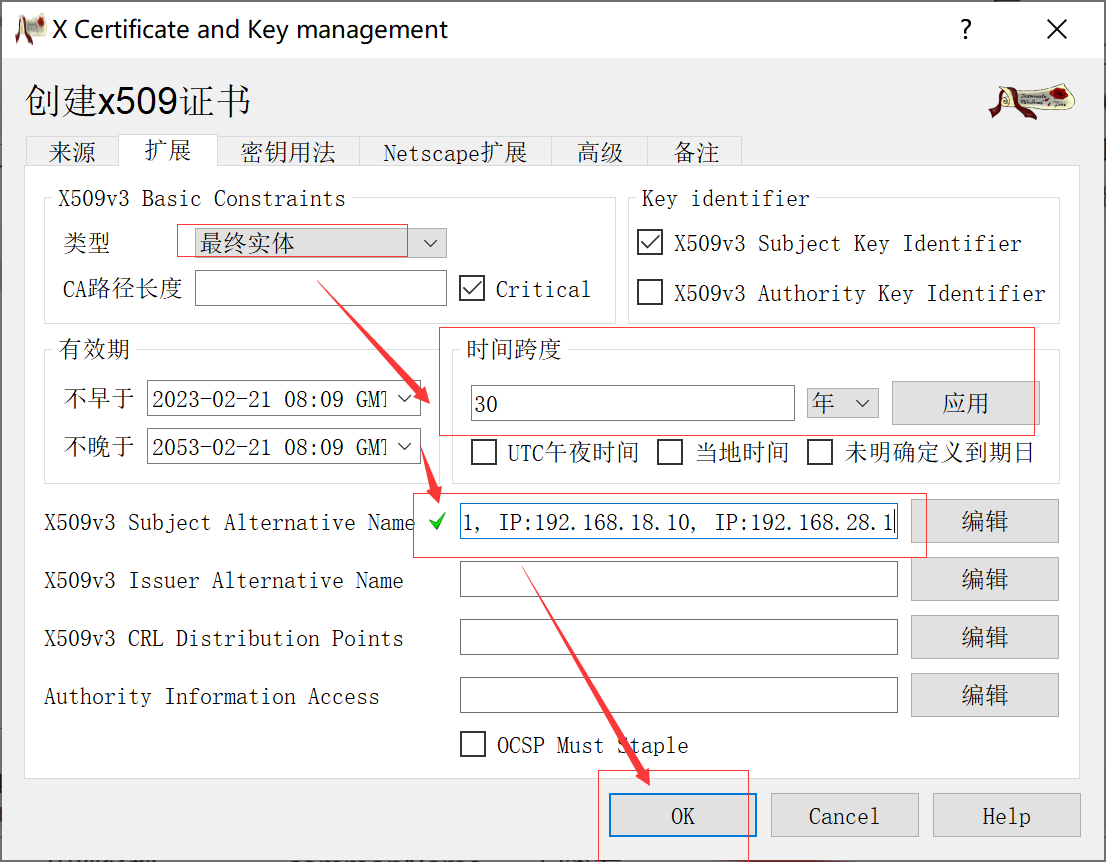
使用xca工具生成自签证书
本文使用 xca 生成自签证书。 概述 之前使用 openssl 生成证书,在 golang 中测试,发现客户端连接失败,经查发现是Subject Alternative Name不支持导致的。因虚拟机 openssl 版本较低,有个功能无法实现,且升级麻烦&…...

Unity IOS 通过命令行导出IPA
新建一个文件然后输入如下内容 #!/usr/bin/env sh /Applications/Unity/Hub/Editor/2020.1.5f1c1/Unity.app/Contents/MacOS/Unity -quit -batchmode -projectPath /Users/zyt/Test -executeMethod Test.BuildEditor.BuildApp cd /Users/zyt/Test/Xcode/unity-xcode xcodebuil…...
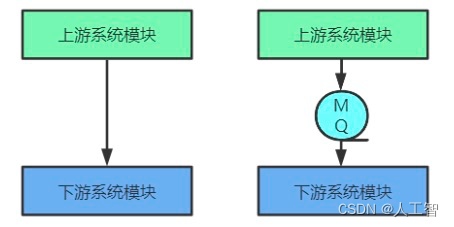
「架构」全链路异步模式
总结自尼恩的全链路异步:网关纯异步化网关层的特点:不需要访问业务数据库只做协议转换和流量转发特点是 IO 密集型,特别适合纯异步的架构,可以极大的节省资源。如何进行网关异步化?使用高性能的通信框架Nettyÿ…...
CleanMyMac4.20最新版新增功能及电脑清理垃圾使用教程
CleanMyMac4.20作为知名的Mac清理工具,仅需一键即可快速而安全地清理系统垃圾,释放磁盘空间,因此一直深受Mac用户的喜爱。在不断更新的版本中,CleanMyMac已经不仅仅满足于只做简单的Mac清理工具,而是为Mac用户提供更多…...

Vue2的tsx开发入门完全指南
本篇文章尽量不遗漏重要环节,本着真正分享的心态,不做标题党 下面进入正题: 由于现在vue的官方脚手架已经非常完善我们就不单独配置webpack了,节省大量的时间成本。 首先使用vue/cli创建一个vue模版项目(记得是vue/…...

GLSL shader学习系列1-Hello World
这是GLSL shader系列第一篇文章,本文学习目标: 安装编辑工具编写hello world程序 安装插件 我使用VSCode编写shader代码,在VSCode上有两个好用的插件需要先装一下: Shader languages support for VS Code glsl-canvas…...

Codeforces Round #851 (Div. 2)(A~D)
A. One and Two给出一个数组,该数组仅由1和2组成,问是否有最小的k使得k位置的前缀积和后缀积相等。思路:计算2个数的前缀和即可,遍历判断。AC Code:#include <bits/stdc.h>typedef long long ll; const int N 1…...

内存保护_1:Tricore芯片MPU模块介绍
上一篇 | 返回主目录 | 下一篇 内存保护_1:Tricore芯片MPU模块介绍1 何为MPU2 MPU相关的硬件子系统2.1 基于地址范围保护逻辑说明2.1.1 地址范围寄存器2.1.2 读、写、执行权限寄存器2.1.3 保护集设置位2.1.4 内存保护功能使能位2.1.5 核的内存保护范围获取说明2.1.6…...

Vue3 -- PDF展示、添加签名(带笔锋)、导出
文章目录笔锋签名方案一实现要点实现过程组件引用页面元素添加引用实现代码效果展示缺点方案二修改页面元素替换引用修改代码效果展示完整代码地址实现功能的时候采用了两个方案,主要是第一个方案最后的实现效果并不太理想,但实现起来比较简单࿰…...
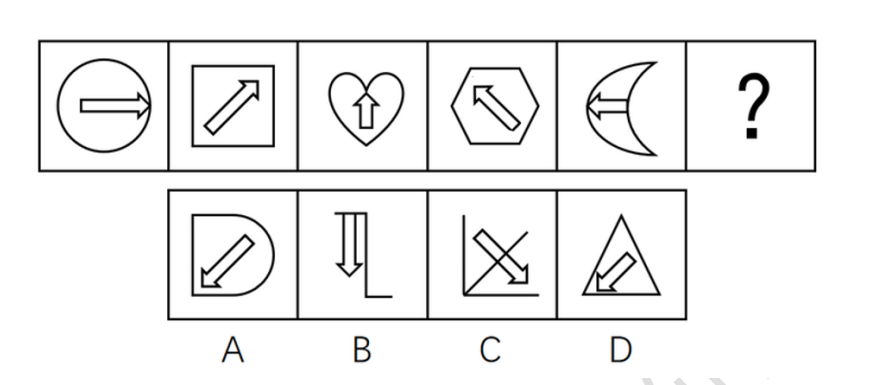
行测-判断推理-图形推理-样式规律-属性规律-曲直性
左边的图全是由曲线构成的选C1 3 5全是由曲线构成的2 4 6全是由直线构成的第三行的图形有曲有直选A1 3 5有曲有直2 4 6全是直线选D图形有曲有直,排除B D外曲内直->内曲外直->外曲内直->内曲外直->外曲内直->内曲外直所以问号出的图形应该是内曲外直选…...

idea集成Alibaba Cloud Toolkit插件
idea集成Alibaba Cloud Toolkit插件 使用该插件主要是简化打包、上传、启动服务的相关操作。 很早之前的方式是使用开发工具(eclipse,idea),使用maven命令完成项目打包(这里指jar),然后通过shell工…...
Win11 文件夹打开慢或卡顿解决方案
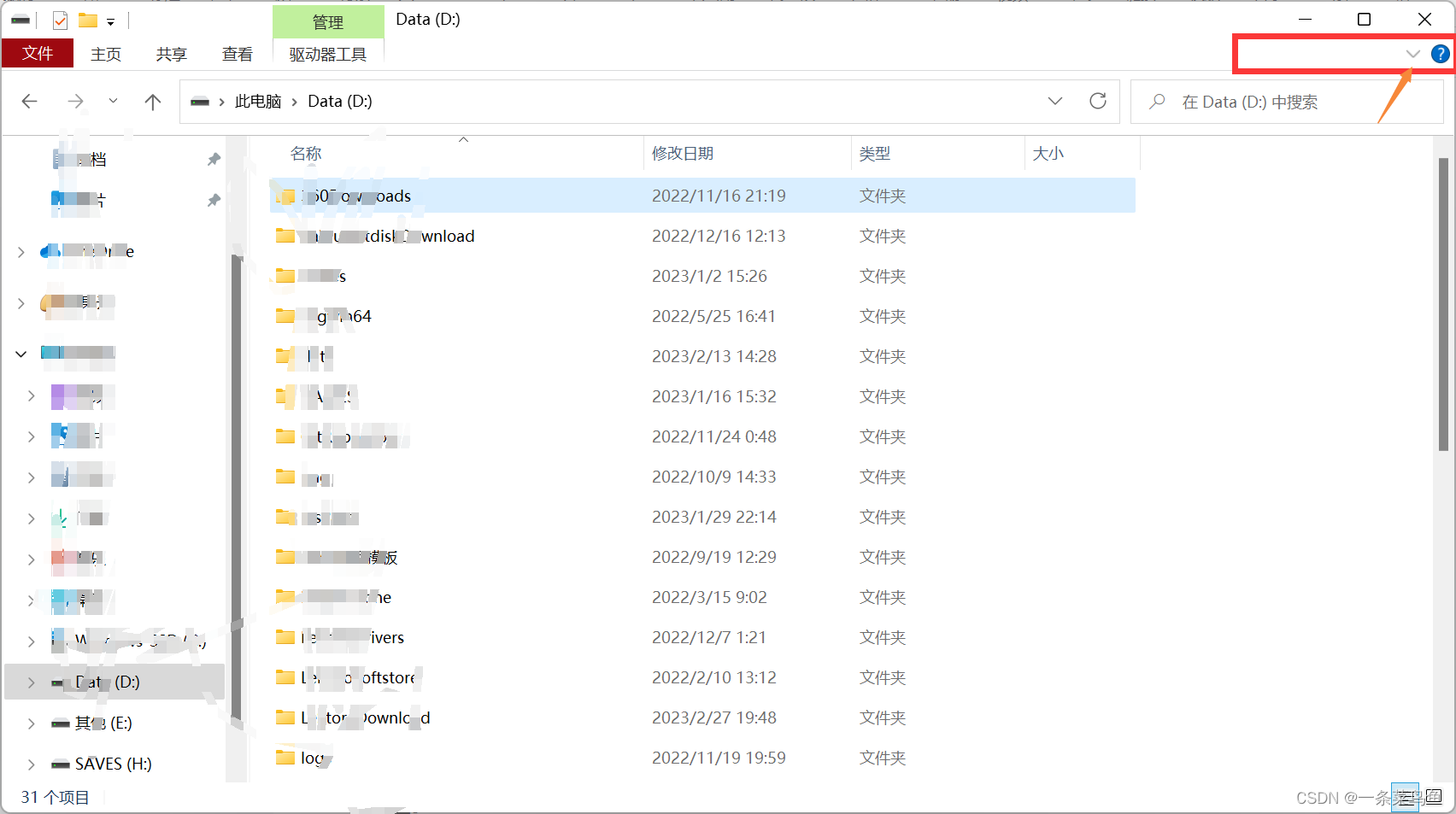
问题 目前是 2023/2/27, 我的 Win11 系统点开一个文件夹要等待 2-3 秒才能加载出来, 使用体验极差。网上查阅大量资料, 有些人在系统更新后这个情况就消失了, 但是我这一直存在, 系统也是当前的最新版, 没有修复。 目前得出的结论是, 因为 Win11 的工具栏占用了过多的资源, 需…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
