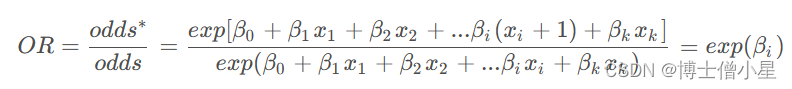科研学习|研究方法——Python计量Logit模型
一、离散选择模型
莎士比亚曾经说过:To be, or not to be, that is the question,这就是典型的离散选择模型。如果被解释变量时离散的,而非连续的,称为“离散选择模型”。例如,消费者在购买汽车的时候通常会比较几个不同的品牌,如福特、本田、大众等。如果将消费者选择福特汽车记为Y=1,选择本田汽车记为Y=2,选择大众汽车记为Y=3;那么在研究消费者选择何种汽车品牌的时候,由于因变量不是一个连续的变量(Y=1, 2, 3),传统的线性回归模型就有一定的局限。
其它的一些常见的离散选择行为的案例还包括:
化妆品牌的选择:雅诗兰黛、兰蔻、欧莱雅...
就餐地点的选择:餐厅甲、餐厅乙、餐厅丙...
旅游风格的选择:自由游、跟团游、自助游...
居住地点的选择:小区A、小区B、小区C...
出行方式的选择:公交、地铁、打车、合乘、自驾、自行车...
二、Logit模型
在统计学里,「概率(Probability)和Odds都是用来描述某件事情发生的可能性的」。Odds指的是 「事件发生的概率」与 「事件不发生的概率」 之比,可以将Odds称为几率或胜率。
「事件A的Odds」 等于 「事件A出现的次数」 和 「其它(非A)事件出现的次数 之比」;相比之下,「事件A的概率」 等于 「事件A出现的次数」 与 「所有事件的次数」 之比。
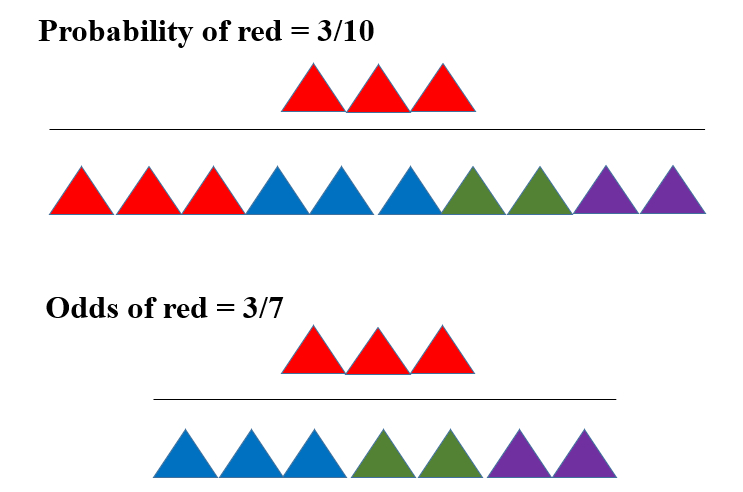
「Odds的对数称之为Logit。」
「从概率P到Odds再到Logit,这就是一个Logit变换。」 Logit 模型可以理解成 Log-it(即it 的自然对数——这里的it指的就是Odds,Logit即the log of an odd)。概率P的取值范围是[0,1],而Logit的取值范围是(-∞,+∞)。概率作为因变量,不能直接套用线性回归模型:
因为线性回归模型的因变量y的范围是,但概率的范围是[0,1]。
由于 Logit的范围是,我们可以将Logit作为因变量,建立线性模型:
方程两边同时exp,可得:
进一步表示为:
Odds Ratio(简称OR)指的是两个几率的比值,称为几率比。举个例子,研究人员怀疑「性别」和「是否会游泳」之间可能存在某种关系,于是按照“性别”和“是否会游泳”对样本进行进划分,结果如下:
| 会游泳 | 不会游泳 | |
|---|---|---|
| 男性 | 100 | 200 |
| 女性 | 100 | 300 |
则男性会游泳的概率为100/300,Odds为100/200,男性会游泳的概率为100/400,Odds为100/300,
则男性相对女性会游泳的Odds Ratio = 100/200/(100/300) =1.5
当OR>1时,分子上的Odds值较大——说明男性会游泳的几率(Odds)更高;若OR=1,则说明性别对是否会游泳没有影响。
三、Logit模型的python实现——采用statsmodels
(一)案例一
以Social_Network_Ads数据为例,演示逻辑回归的Python操作。数据文件一共400条数据,前面四列是用户ID(User ID)、性别(Gender)、年龄(Age)、大致薪水(EstimatedSalary),第五列为是否购买(Purchased),没购买是0,购买是1。数据源文件链接:https://pan.baidu.com/s/1HA6prrhdenNnI76G5QryMw 提取码:zul4。
首先导入相关库。
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import statsmodels.api as sm
from patsy import dmatrices
用pandas的「read_csv」函数读取原始数据文件。
data = pd.read_csv(r'C:\Users\mi\Downloads\Social_Network_Ads.csv')
在Spyder的变量浏览器中,可查看data变量。
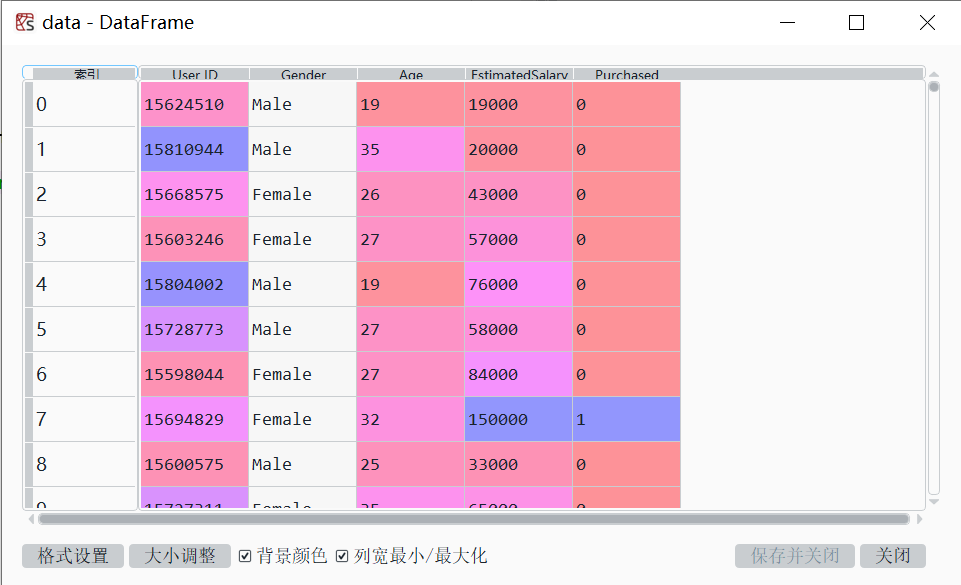
可查看data信息。
print(data.info())
结果为:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 400 entries, 0 to 399
Data columns (total 5 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 User ID 400 non-null int64 1 Gender 400 non-null object 2 Age 400 non-null float643 EstimatedSalary 400 non-null float644 Purchased 400 non-null int64
dtypes: float64(2), int64(2), object(1)
memory usage: 15.8+ KB
用DataFrame的「describe」()函数对样本中的各变量做描述性分析,结果如下面所示。我们可以得到每一个变量的出现的频数(count)、均值(mean)、标准差(std)、最大/小值(min/max)、百分位数(25%,50%,75%)等信息。
print(data.describe())
结果为:
User ID Age EstimatedSalary Purchased
count 4.000000e+02 400.000000 400.000000 400.000000
mean 1.569154e+07 37.655000 69742.500000 0.357500
std 7.165832e+04 10.482877 34096.960282 0.479864
min 1.556669e+07 18.000000 15000.000000 0.000000
25% 1.562676e+07 29.750000 43000.000000 0.000000
50% 1.569434e+07 37.000000 70000.000000 0.000000
75% 1.575036e+07 46.000000 88000.000000 1.000000
max 1.581524e+07 60.000000 150000.000000 1.000000
接下来进行Logit回归,有基于公式和基于数组两种方法。
「方法一:基于公式」
import statsmodels.formula.api as smflogit = smf.logit(formula='Purchased ~ Age + EstimatedSalary + Gender', data = data)
results = logit.fit()
print(results.summary())
「方法二:基于数组」
调用Logit() 函数的基本格式为:
sm.Logit(endog,exog)
代码如下:
import statsmodels.api as sm
from patsy import dmatricesy,X = dmatrices('Purchased ~ Age + EstimatedSalary + Gender',data = data,return_type='dataframe')logit = sm.Logit(y,X)
results = logit.fit()
print(results.summary())
方法一和方法二的结果一致,为:
Logit Regression Results
==============================================================================
Dep. Variable: Purchased No. Observations: 400
Model: Logit Df Residuals: 396
Method: MLE Df Model: 3
Date: Sat, 20 Aug 2022 Pseudo R-squ.: 0.4711
Time: 11:33:28 Log-Likelihood: -137.92
converged: True LL-Null: -260.79
Covariance Type: nonrobust LLR p-value: 5.488e-53
===================================================================================coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept -12.7836 1.359 -9.405 0.000 -15.448 -10.120
Gender[T.Male] 0.3338 0.305 1.094 0.274 -0.264 0.932
Age 0.2370 0.026 8.984 0.000 0.185 0.289
EstimatedSalary 3.644e-05 5.47e-06 6.659 0.000 2.57e-05 4.72e-05
===================================================================================
上表中输出了Logit模型的相关拟合结果。结果包含两部分:上半部分给出了和模型整体相关的信息,包括因变量的名称(Dep. Variable: Purchased)、模型名称(Model: Logit)、拟合方法(Method: MLE 最大似然估计)等信息;下半部分则给出了和每一个系数相关的信息,包括系数的估计值(coef)、标准误(std err)、z统计量的值、显著水平(P>|z|)和95%置信区间。
根据上表可以得到本例中Logit模型的具体形式:
Logit模型变量的系数是指:「自变量每变化一个单位,几率(Odds)的对数的变化值」。在本例中,以变量「Age」的系数为例,其解读方式为:当其它变量保持不变时,申请者的Age年龄每增加一岁,其购买汽车的对数几率增加0.2370(绝对数),对数几率并不易直观理解。由于取对数约等于百分比的变化,故可理解为几率约增加23.70%(相对数)。
假设变化一单位,从变为,记几率odd的新值为,则可根据新几率与原几率odd的比率定义几率比。
or = np.exp(results.params)
print(or)
结果为:
Intercept 0.000003
Gender[T.Male] 1.396324
Age 1.267402
EstimatedSalary 1.000036
dtype: float64
在本例中,以变量「Age」的OR为例,其解读方式为:当其它变量保持不变时,申请者的Age年龄每增加一岁,其购买汽车的几率变为原来的1.267倍,即几率增加了26.7%。
如果想计算每个变量的“边际效应”,可使用get_margeff()方法,并将所得结果用summary()方法展示。
什么是边际效应呢?即,概率对自变量求导数。
get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)
其参数说明如下:
| 参数 | 说明 |
|---|---|
| at | ‘overall’, 平均边际效应,默认. ‘mean’, 样本均值处的边际效应. ‘median’, 样本中值处的边际效应. |
| method | 'dydx’ - dy/dx, ‘eyex’ - d(lny)/d(lnx) ,‘dyex’ - dy/d(lnx) ,‘eydx’ - d(lny)/dx |
计算平均边际效应:
margeff = results.get_margeff()
print(margeff.summary())
结果如下:
=====================================
Dep. Variable: Purchased
Method: dydx
At: overall
===================================================================================dy/dx std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
Gender[T.Male] 0.0368 0.034 1.099 0.272 -0.029 0.103
Age 0.0262 0.001 18.674 0.000 0.023 0.029
EstimatedSalary 4.022e-06 4.55e-07 8.840 0.000 3.13e-06 4.91e-06
===================================================================================
结果解释:当保持其他变量的取值不变时,男性买车的概率比女性高3.68%;当保持其他变量的取值不变时,年龄每增加一岁,买车的概率高2.62%。
(二)案例二
以titanic数据为例,演示逻辑回归的Statsmodels操作。数据链接:https://pan.baidu.com/s/1ipxk-hMWQasHefOX4mMC-w 提取码:07wv
首先导入相关库。
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import statsmodels.api as sm
from patsy import dmatrices
用pandas的「read_csv」函数读取原始数据文件。
titanic = pd.read_csv(r'C:\Users\mi\Downloads\MLPython_Data\titanic.csv')
在Spyder的变量浏览器中,可查看titanic变量。
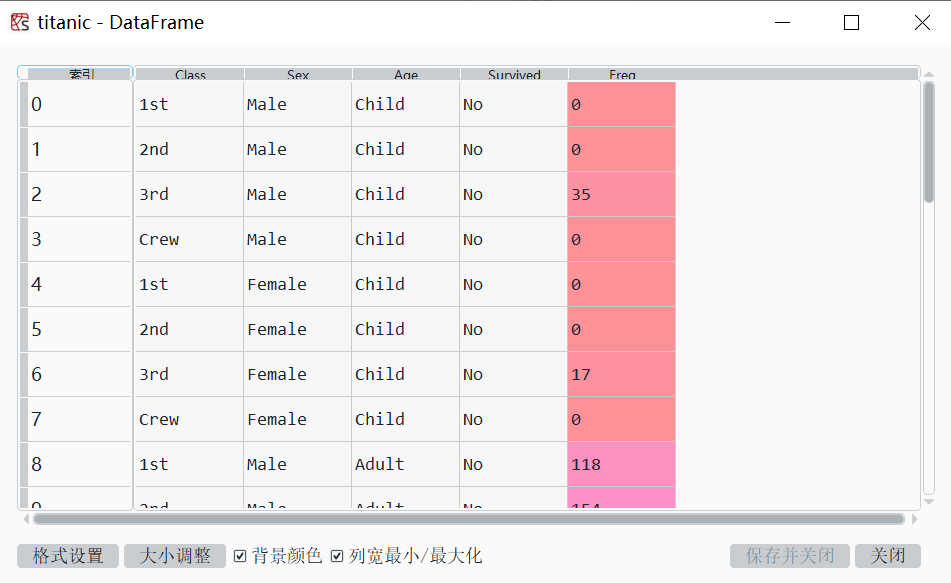
数据框的最后一个变量Freq,表示每个观测值在样本中出现的次数。因变量Survived取值为Yes或No,表示是否存活。因变量包括Age(取值为Child或Adult),Sex(取值为Male或Female),以及Class(取值为1st,2nd,3rd或Crew,分别表示头等舱、二等舱、三等舱与船员)。
需要将数据框完全展开,根据变量Freq让不同的观测值在数据框中以相应的频次出现。为此,使用to_numpy()方法,将变量Freq变为数组,并记为freq:
freq = titanic.Freq.to_numpy()
然后,使用np.repeat()函数,将np.arange(len(titanic))中每个元素,按照freq的频率进行重复,并记所得数组为index:
index = np.repeat(np.arange(len(titanic)),freq)
利用数据框的索引方法,可得整个样本:
titanic = titanic.iloc[index,:]
然后,去掉变量Freq:
titanic = titanic.drop('Freq',axis=1)
获取的titanic数据框如下:

可查看titanic数据框信息。
print(titanic.info())
结果为:
<class 'pandas.core.frame.DataFrame'>
Int64Index: 2201 entries, 2 to 31
Data columns (total 4 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 Class 2201 non-null object1 Sex 2201 non-null object2 Age 2201 non-null object3 Survived 2201 non-null object
dtypes: object(4)
memory usage: 86.0+ KB
None
接下来进行Logit回归,有基于公式和基于数组两种方法。
「方法一:基于公式」
由于因变量survived是字符型的分类变量,如果不对survived做处理,则会报错。

image-20220822150240414
错误代码:
import statsmodels.formula.api as smflogit = smf.logit(formula='Survived ~ Class + Sex + Age', data = titanic)
results = logit.fit()
print(results.summary())
返回结果:
ValueError: endog has evaluated to an array with multiple columns that has shape (2201, 2). This occurs when the variable converted to endog is non-numeric (e.g., bool or str).
「回归时,若涉及虚拟变量,虚拟因变量必须是数值型的“虚拟变量”,而虚拟自变量可以是字符型的“分类变量”,也可以数值型的“虚拟变量”。」
本例中,自变量和因变量均是字符型的“分类变量”,因变量可以转变为数值型的“虚拟变量”,也可以不转变。
因此需要将代码修改为:
import statsmodels.formula.api as smftitanic['Survived'] = (titanic['Survived'] == 'Yes').astype(int) # False=0, True=1
logit = smf.logit(formula='Survived ~ Class + Sex + Age', data = titanic)
results = logit.fit()
print(results.summary())
「方法二:基于数组」
调用Logit() 函数的基本格式为:
sm.Logit(endog,exog)
本例中,自变量和因变量均是字符型的“分类变量”,可使用dmatrices()函数将字符型的“分类变量”统一转变为数字型的“虚拟变量”。
y,X = dmatrices('Survived ~ Class + Sex + Age',data = titanic,return_type='dataframe')
查看y、X数据框。
因变量y:包含两个虚拟变量,即”Survived[No]“和”Survived[Yes]“,而我们仅需要其中一个。为此,保留”Survived[Yes]“。
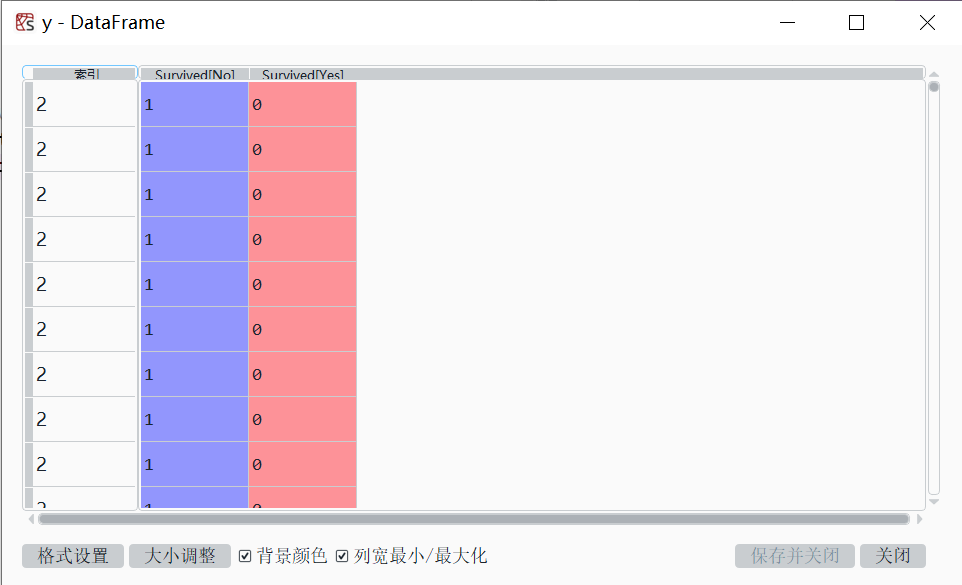
y= y.iloc[:,1]

自变量X:已根据原来的分类变量生成了相应的虚拟变量,并去掉了多余的参照类别。比如,对于分类变量Sex,去掉了Sex[T.Female],仅保留Sex[T.Male]。其中,'T.male'的前缀”T“表示”Treatment“。
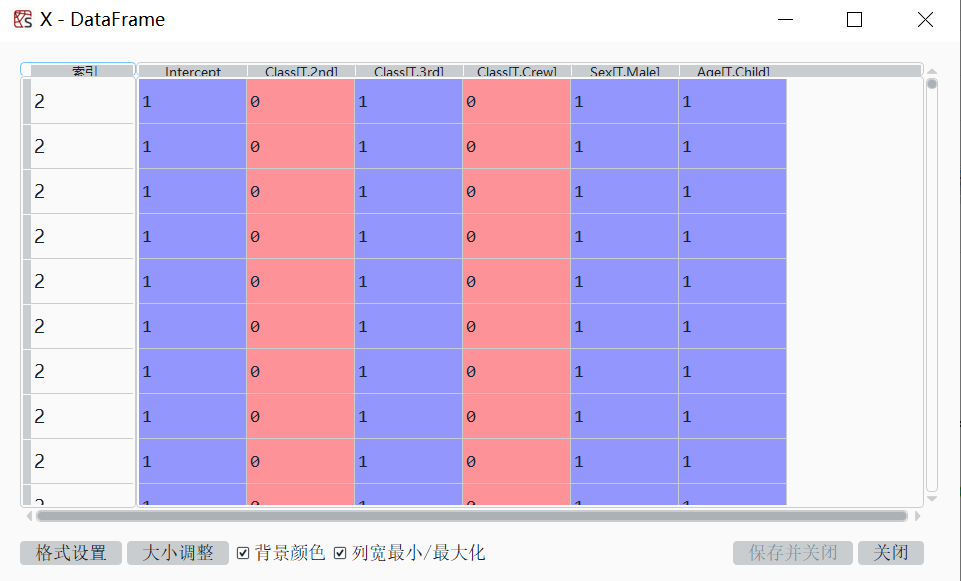
完整代码为:
import statsmodels.api as sm
from patsy import dmatricesy,X = dmatrices('Survived ~ Class + Sex + Age',data = titanic,return_type='dataframe')
y= y.iloc[:,1]logit = sm.Logit(y,X)
results = logit.fit()
print(results.summary())
方法一和方法二的结果一致,为:
Logit Regression Results
==============================================================================
Dep. Variable: Survived No. Observations: 2201
Model: Logit Df Residuals: 2195
Method: MLE Df Model: 5
Date: Mon, 22 Aug 2022 Pseudo R-squ.: 0.2020
Time: 15:06:41 Log-Likelihood: -1105.0
converged: True LL-Null: -1384.7
Covariance Type: nonrobust LLR p-value: 1.195e-118
=================================================================================coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 2.0438 0.168 12.171 0.000 1.715 2.373
Class[T.2nd] -1.0181 0.196 -5.194 0.000 -1.402 -0.634
Class[T.3rd] -1.7778 0.172 -10.362 0.000 -2.114 -1.441
Class[T.Crew] -0.8577 0.157 -5.451 0.000 -1.166 -0.549
Sex[T.Male] -2.4201 0.140 -17.236 0.000 -2.695 -2.145
Age[T.Child] 1.0615 0.244 4.350 0.000 0.583 1.540
=================================================================================相关文章:

科研学习|研究方法——Python计量Logit模型
一、离散选择模型 莎士比亚曾经说过:To be, or not to be, that is the question,这就是典型的离散选择模型。如果被解释变量时离散的,而非连续的,称为“离散选择模型”。例如,消费者在购买汽车的时候通常会比较几个不…...

灵活运用Vue指令:探究v-if和v-for的使用技巧和注意事项
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、作…...

nvidia-docker部署pytorch服务【GPU工作站】
文章目录 一、安装 Docker二、安装 NVIDIA Container Toolkit三、宿主机安装 cuda 和 nvidia-driver四、测试一、安装 Docker 可以参考这篇文章 https://blog.csdn.net/weixin_43721000/article/details/124237932 二、安装 NVIDIA Container Toolkit 参考nvidia官方 https:/…...
单链表的实现
CSDN主页:醋溜马桶圈_C语言进阶,初始C语言,数据结构-CSDN博客 Gitee主页:mnxcc (mnxcc) - Gitee.com 专栏:数据结构_醋溜马桶圈的博客-CSDN博客 目录 1.认识单链表 2.创建单链表 3.单链表的操作 3.1打印单链表 3.2开辟新空间 3.3尾插 3.4头插…...
)
【python】面向对象(类型定义魔法方法)
目录 一、引言 二、类型定义 1、什么是类型的定义? 2、案例 三、魔法方法 1、什么是魔法方法 2、基础部分 3、比较操作 4、容器类型 5、属性管理 6、封装 7、方法拓展 8、继承 9、多态 一、引言 Python是一种面向对象的语言,它支持类&#…...
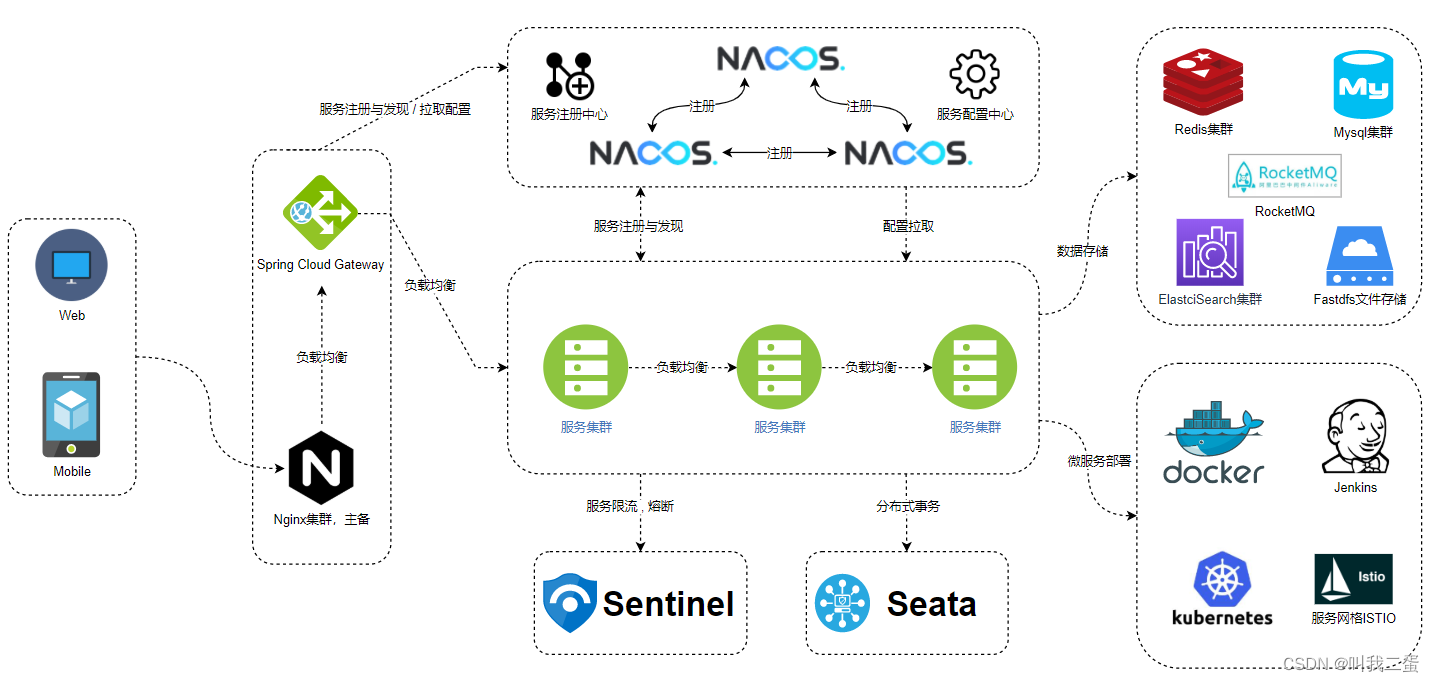
1.微服务与SpringCloud
微服务和SpringCloud 文章目录 微服务和SpringCloud1.什么是微服务2.SpringCloud3. 微服务 VS SpringCloud4. SpringCloud 组件5.参考文档6.版本要求 1.什么是微服务 微服务是将一个大型的、单一的应用程序拆分成多个小型服务,每个服务实现特定的业务功能ÿ…...
【2023全网最全最火】Selenium WebDriver教程(建议收藏)
在本教程中,我将向您介绍 Selenium Webdriver,它是当今市场上使用最广泛的自动化测试框架。它是开源的,可与所有著名的编程语言(如Java、Python、C#、Ruby、Perl等)一起使用,以实现浏览器活动的…...
)
dimp 导入dmp文件报错:无效的模式名(DM8:达梦数据库)
dimp 导入dmp文件报错:无效的模式名-DM8:达梦数据库 环境介绍1 搭建A1 数据库52361.1 A1数据库5236创建模式名,表,测试数据1.2 从A1数据库5236导出dmp文件 2 搭建A2数据库52372.1 创建 数据用户ABC2311152.2 在A2 数据库5237 导入DMP(报错无效的模式名)2.3 使用REMAP_SCHEMAABC…...
)
宿主机无法连接docker里的redis问题解决(生产环境慎用)
宿主机无法连接docker里的redis问题解决(生产环境慎用) 问题描述解决方案 问题描述 1.连接超时 2.连接能连上但马上断开并报错 3.提示保护模式什么的 (error) DENIED Redis is running in protected mode because protected mode is enabled链接redis …...
给女朋友开发个小程序低价点外卖吃还能赚钱
前言 今天又是无聊的一天,逛了下GitHub,发现一个库里面介绍美团饿了吗外卖红包外卖优惠券,先领红包再下单。外卖红包优惠券,cps分成,别人领红包下单,你拿佣金。哇靠,那我岂不是可以省钱还可以赚钱,yyds。。。。想想都美好哈哈哈!!! 回到正题,这个是美团饿了么分销…...

外贸客户管理系统是什么?推荐的管理软件?
外贸客户管理系统哪个好用?海洋建站如何选管理系统? 外贸客户管理系统,是一款专为外贸企业设计的客户关系管理系统,旨在帮助外贸企业建立与维护客户关系,提高客户满意度和忠诚度,提升企业业绩。海洋建站将…...

数据挖掘:分类,聚类,关联关系,回归
数据挖掘: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤其sql要学&…...

力扣labuladong一刷day10一网打尽股票买卖问题共6题
力扣labuladong一刷day10股票买卖问题共6题 一、121. 买卖股票的最佳时机 题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 思路:只能买入1次,定义dp[i][0]数组表示第i天持有股票时手中的最大金额 数,…...

微信小程序手写table表格
wxml <view class"table"><view class"tr bg-w"><view class"th">张三</view><view class"th" style"color: #409eff;">李四</view><view class"th ">王五</view&…...
UE5 - UI Material Lab 学习笔记
1、学习资料收集 UI Material Lab : https://www.unrealengine.com/marketplace/zh-CN/product/ui-material-lab 视频1:https://www.bilibili.com/video/BV1Hm4y1t7Kn/?spm_id_from333.337.search-card.all.click&vd_source707ec8983cc32e6e065d5496a7f79ee6 视…...

oracle删除重复的数据
去除重复数据: group by 对要比对的字段进行查询是否重复 CREATE TABLE 临时表 AS (select 字段1,字段2,count(*) from 表名 group by 字段1,字段2 having count(*) > 1) 上面这句话就是建立了临时表,并将查询到的数据插入其中。 下面就可以进行…...

Python中的并发编程是什么,如何使用Python进行并发编程?
Python中的并发编程是指使用多线程或多进程来同时执行多个任务。这样可以提高程序的执行效率,特别是在处理I/O密集型任务时。Python提供了多种方式来实现并发编程,如threading模块和multiprocessing模块。 使用Python进行并发编程的方法如下:…...

【LeetCode】136. 只出现一次的数字
136. 只出现一次的数字 难度:简单 题目 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用…...

HTTP服务器——tomcat的安装和使用
文章目录 前言下载tomcattomcat 文件bin 文件夹conf 文件lib 文件log 文件temp 文件webapps 文件work 目录 如何使用 tomcat 前言 前面我们已经学习了应用层协议 HTTP 协议和 HTTP 的改进版——HTTPS,这些协议是我们在写与服务器相关的代码的时候息息相关的&#x…...
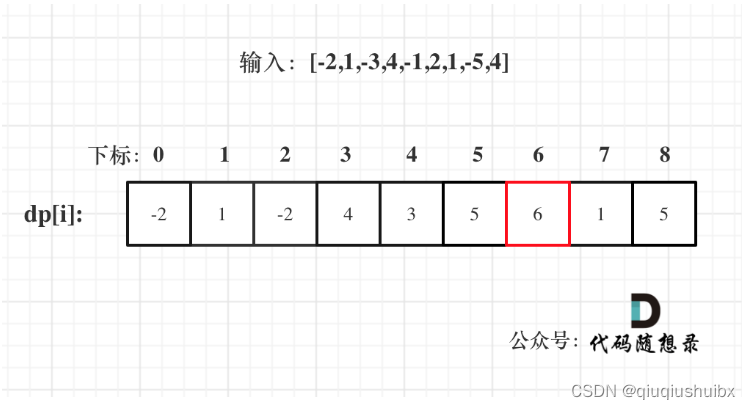
代码随想录Day45 动态规划13 LeetCode T1143最长公共子序列 T1135 不相交的线 T53最大子数组和
LeetCode T1143 最长公共子序列 题目链接:1143. 最长公共子序列 - 力扣(LeetCode) 题目思路: 动规五部曲分析 1.确定dp数组的含义 这里dp数组的含义是结尾分别为i-1,j-1的text1和text2的最长公共子序列长度 至于为什么是i-1,j-1我之前已经说过了,这里再…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...