代码随想录Day45 动态规划13 LeetCode T1143最长公共子序列 T1135 不相交的线 T53最大子数组和
LeetCode T1143 最长公共子序列
题目链接:1143. 最长公共子序列 - 力扣(LeetCode)

题目思路:
动规五部曲分析
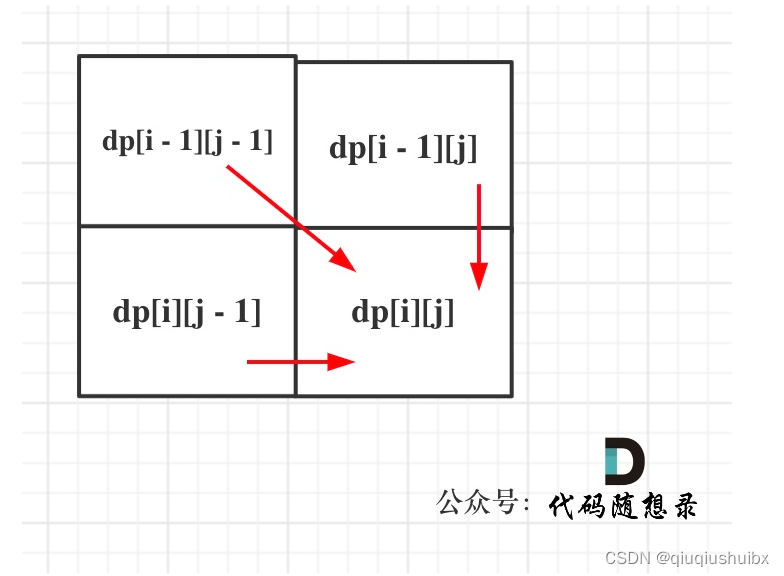
1.确定dp数组的含义
这里dp数组的含义是结尾分别为i-1,j-1的text1和text2的最长公共子序列长度
至于为什么是i-1,j-1我之前已经说过了,这里再说一次,因为如果定义为i和j 的话就需要比较两个字符串的首字母分别是否相等来初始化dp[0][i]和dp[0][j],因为这样定义的话dp[0][j]和 dp[i][0]就没有含义,省去了初始化的部分
2.确定递推公式
dp[i][j]可以从dp[i-1][j-1],dp[i-1][j]和dp[i][j-1]三个推出来
当text1[i]和text2[j]相等时,就是dp[i-1][j-1]+1
当两者不相等时,就是剩下两者的最大值
3.初始化dp数组
无需初始化,原因上面说清楚了,而剩下的所有值都会被覆盖,所以无所谓
4.遍历顺序
从前向后,因为后面的数据是前面产生的
5.打印排错
题目代码:
class Solution {public int longestCommonSubsequence(String text1, String text2) {int dp[][] = new int[text1.length()+1][text2.length()+1];for(int i = 1;i<=text1.length();i++){char c = text1.charAt(i-1);for(int j = 1;j<=text2.length();j++){char c2 = text2.charAt(j-1);if(c == c2){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[text1.length()][text2.length()];}
}LeetCode T1135 不相交的线
题目链接:1035. 不相交的线 - 力扣(LeetCode)


题目思路:
这里我们可以将这一题的思路转化一下,其实就和第一题的思路一模一样,题目要求两条对应的线不能相交,其实就是交代了有序性,这也满足了第一题的条件,求最长公共子序列,所以不做过多赘述.
题目代码:
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length+1][nums2.length+1];int res = 0;for(int i = 1;i<=nums1.length;i++){for(int j = 1;j<=nums2.length;j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[nums1.length][nums2.length];}
}LeetCode T53 最大子数组和
题目链接:53. 最大子数组和 - 力扣(LeetCode)
题目思路:
动规五部曲分析
1.确定dp数组的含义
这里dp数组的含义是i位置之前(包括i在内)最大连续子序列之和
这一题我们在之前也用过贪心的思路来求解,见文章
代码随想录 Day26 贪心 01 全集 LeetCode455 分发饼干 LeetCodeT346摆动序列 LeetCdoe T53 最大子数组和-CSDN博客
2.确定递推公式
dp[i][j]可以从前面一个推出,如果累计和小于当前的nums[i],就从nums[i]开始记录
3.初始化dp数组
dp[0] = nums[0];不能初始化为0,因为有一个元素的情况存在
4.遍历顺序
从前向后遍历即可
5.打印排错
注意:这题的结果不在结尾取,要定义一个res在赋值的时候顺便记录最大值
题目代码:
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int res = dp[0];for(int i = 1;i<nums.length;i++){dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);res = Math.max(res,dp[i]);}return res;}
}相关文章:
代码随想录Day45 动态规划13 LeetCode T1143最长公共子序列 T1135 不相交的线 T53最大子数组和
LeetCode T1143 最长公共子序列 题目链接:1143. 最长公共子序列 - 力扣(LeetCode) 题目思路: 动规五部曲分析 1.确定dp数组的含义 这里dp数组的含义是结尾分别为i-1,j-1的text1和text2的最长公共子序列长度 至于为什么是i-1,j-1我之前已经说过了,这里再…...

写了个监控 ElasticSearch 进程异常的脚本!
服务器配置免密钥环境准备: 配置免密钥前,需要在服务器的 hosts 文件中配置目标主机名称与 IP 对应关系。 vim /etc/hosts IP1 hostname1 IP2 hostname2 ...... 将 mianmiyaojiaoben.zip 安装包解压在当前目录下 cd /usr/local/jiaoben unzip mianmi…...
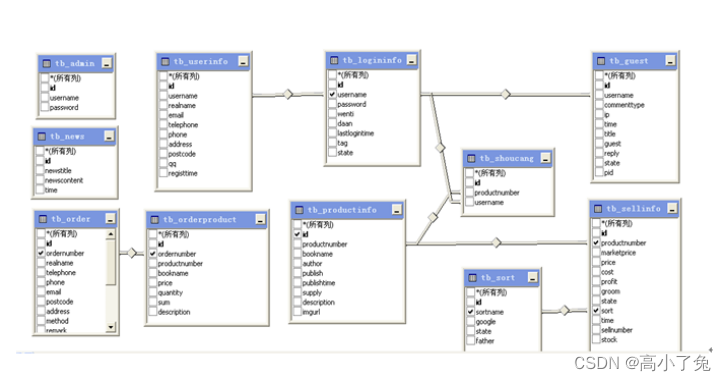
第三篇 基于JSP 技术的网上购书系统—— 数据库系统设计(网上商城、仿淘宝、当当、亚马逊)
目录 1.逻辑关系设计 2.物理设计 2.1管理员表 2.2留言表 2.3会员登录表 2.4会员表 2.5订单表 2.6订单商品表 2.7产品表 2.8产品货架表 2.9收藏表 2.10类别表 2.11新闻表 数据库系统是用来保存数据的软件系统,当今比较流行的数据库系统,如 MS…...

电脑检测温度软件有哪些?
环境: Win10 专业版 问题描述: 电脑检测温度软件有哪些? 解决方案: 有很多电脑检测温度的软件可供选择,以下是一些常用的电脑温度监测工具: HWMonitor:一款免费的硬件监控软件࿰…...
)
设计模式 -- 单例模式(Singleton Pattern)
单例模式:最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保只有单个对象被创建。这个类提供了一种访问其唯一的对象的方式…...

ubuntu给终端加代理服务器
ubuntu给终端加代理 访问google.com 是否可以访问通 curl https://www.google.com如果访问不通说明代理服务器没有配置好。 使用 gedit ~/.bashrc 打开网络配置 gedit ~/.bashrc找到文章的最后添加代理 export http_proxyhttp://127.0.0.1:7890 export https_proxyhttp://…...

centos 6.10 安装 readline 6.2.0
下载地址 解压文件 cd readline-6.2 ./configure -prefix /usr/local/readline-6.2 make && make install安装完成...
IDEA 2023搭建 SpringMVC +FreeMarker+JDBC
1.IDEA的版本,目前最新是2023,要选择旗舰版。笔者曾选择社区版,发现少了很多功能。只能重新安装。 2.安装好以后的第1件事,是设置Maven,并将下载地址改为淘定站,参照这篇一次包会——最新IDEA配置Maven指南…...

RabbitMQ传统数据持久化和Lazy queue的区别
问题引出: 在了解这个问题前我们需要一些前置知识: 关于MQ可靠性,在默认情况下,RabbitMQ会将接收到的信息保存在内存中以降低消息收发的延迟。这样会导致两个问题: 一旦MQ宕机,内存中的信息会丢失 内存空…...

docker部署lnmp环境
文章目录 前期准备:一、部署mysql1.1 获取 Mysql 5.7.22 镜像1.2 启动mysql容器 二、部署php2.1 获取php 7.2镜像2.2 启动php 容器2.3 php的扩展安装 三、部署nginx3.1 获取nginx:1.14镜像3.2 启动nginx容器3.3 编写nginx虚拟主机配置文件,使其支持php3.…...
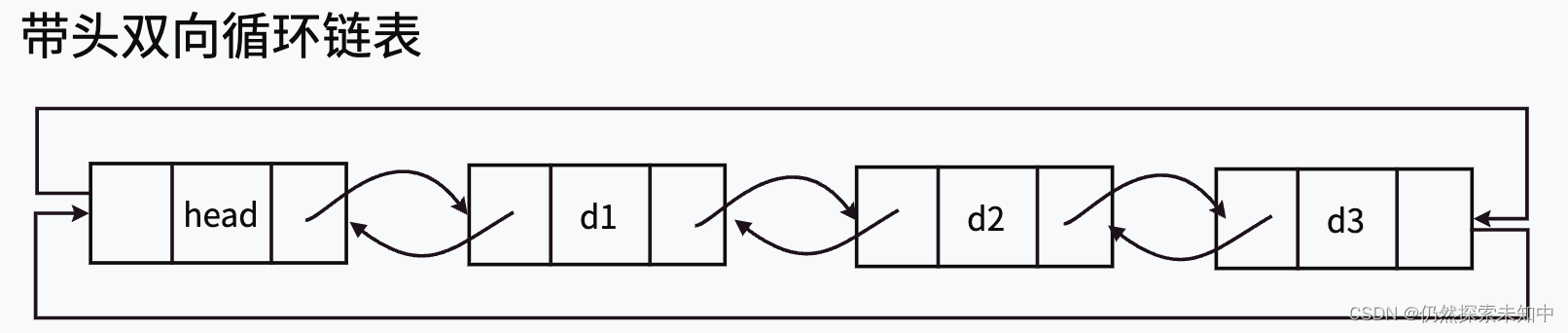
数据结构 | 带头双向循环链表专题
数据结构 | 带头双向循环链表专题 前言 前面我们学了单链表,我们这次来看一个专题带头的双向循环链表~~ 文章目录 数据结构 | 带头双向循环链表专题前言带头双向循环链表的结构实现双向链表头文件的定义创建节点哨兵位初始化尾插尾删头插头删打印查找指定位置前插入…...
批量处理)
Redis使用Pipeline(管道)批量处理
Redis 批量处理 在开发中,有时需要对Redis 进行大批量的处理。 比如Redis批量查询多个Hash。如果是在for循环中逐个查询,那性能会很差。 这时,可以使用 Pipeline (管道)。 Pipeline (管道) Pipeline (管道) 可以一次性发送多条命令并在执…...
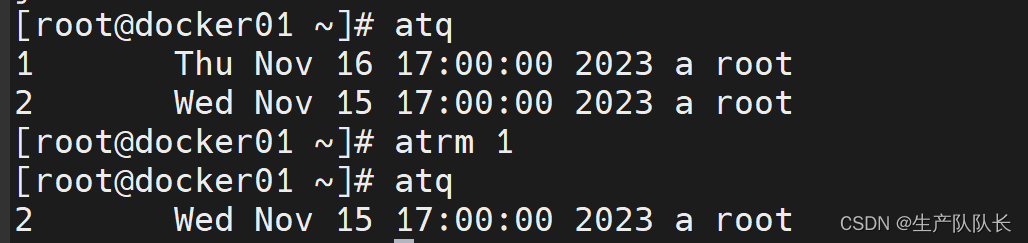
Linux中at命令添加一次性任务
1、工作原理 功能:在某个时间点,执行一次命令。 特点:任务是用户隔离的。 条件:必须要保证atd进程存在。 ps -ef |grep atd 原理:atd进程循环遍历队列里的任务,有任务,且到达执行时间ÿ…...
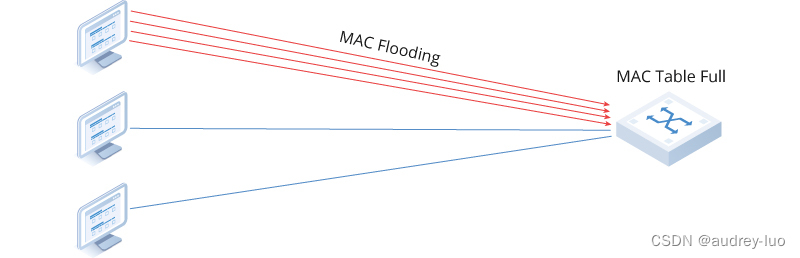
交换机基础知识之安全配置
交换机在网络基础设施中扮演着重要角色,它促进了设备之间数据包的流动。正因此,采取适当的安全措施来保护网络免受未经授权的访问和潜在攻击至关重要。本文将全面解读交换机基础安全配置知识,并提供实践方案,以保证安全的网络环境…...
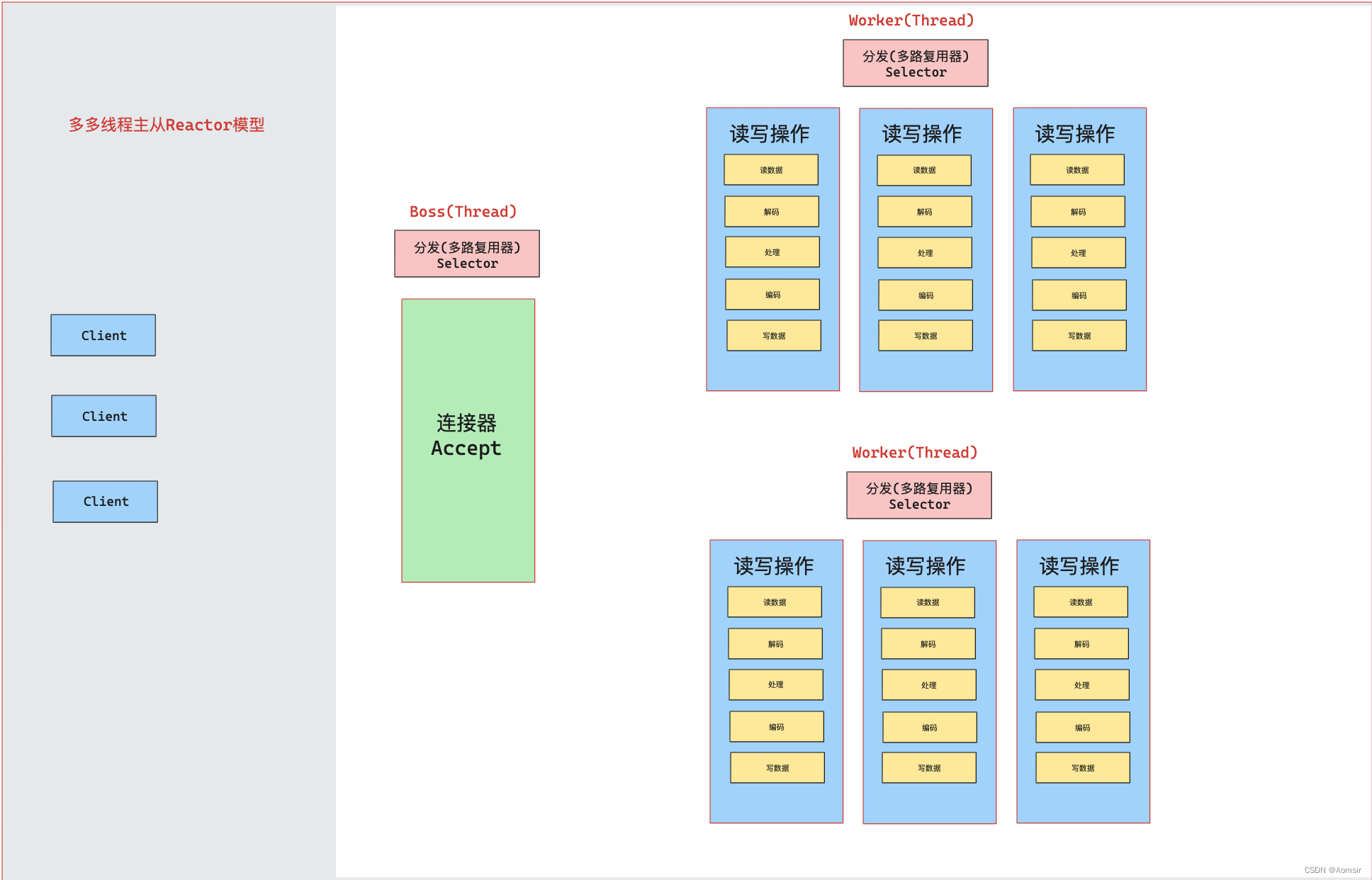
Netty入门指南之Reactor模型
作者简介:☕️大家好,我是Aomsir,一个爱折腾的开发者! 个人主页:Aomsir_Spring5应用专栏,Netty应用专栏,RPC应用专栏-CSDN博客 当前专栏:Netty应用专栏_Aomsir的博客-CSDN博客 文章目录 参考文献前言单线程…...

Ubuntu20.04软件安装顺序
目录 0.网卡驱动1. sogoupinyin2. terminator3.1zsh3.2升级Cmake(有些后面的软件需要高版本Cmake)4.显卡驱动(在cuda之前)5.CUDA与cudnn,TensorRT6.OpenCV(在ROS之前)6.1先安装各种依赖6.2安装Ceres-1.14.06.3安装Pangolin6.4安装Sophus6.5安装VTK6.5编译…...

适配器模式 ( Adapter Pattern )(6)
适配器模式 ( Adapter Pattern ) 适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁 适配器模式涉及到一个单一的类,该类负责加入独立的或不兼容的接口功能 举个真实的例子,读卡器是作为内存卡和笔记本之间的适配器…...
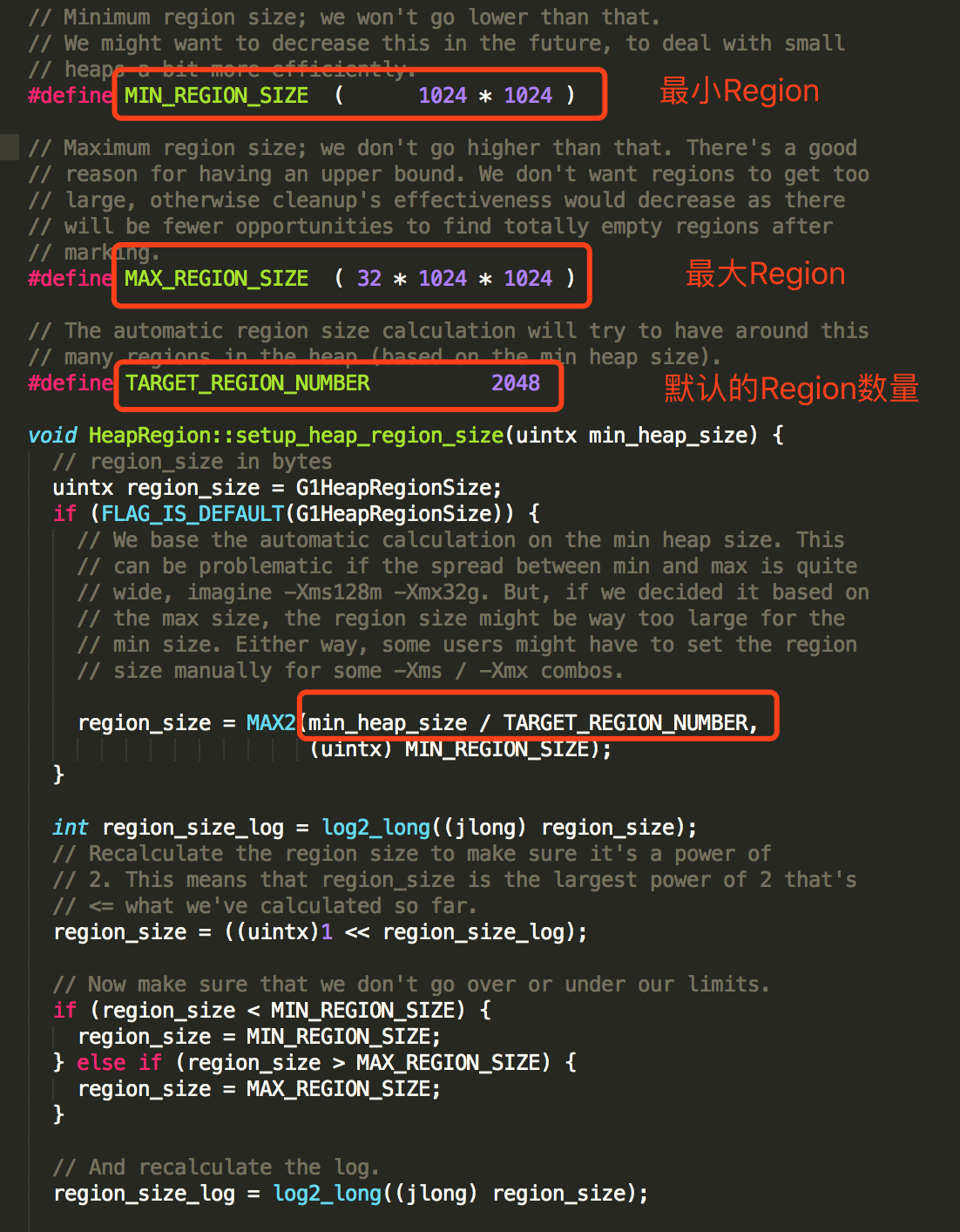
JAVA G1垃圾收集器介绍
为解决CMS算法产生空间碎片和其它一系列的问题缺陷,HotSpot提供了另外一种垃圾回收策略,G1(Garbage First)算法,通过参数-XX:UseG1GC来启用,该算法在JDK 7u4版本被正式推出,官网对此描述如下&am…...

十方影视后期“领进门”,成长与成就还得靠自身
在这个充满视觉冲击的时代,影视后期制作已经成为了一种炙手可热的艺术形式。而在这个领域,Adobe After Effects(AE)这款软件无疑是王者之一。十方影视后期作为十方教育科技旗下的艺术设计学科,不仅培养了数万名优秀的后…...

Golang之火爆原因
引言 在计算机编程领域,有很多种编程语言可供选择。然而,近年来,Golang(Go)这门相对年轻的编程语言却越来越受欢迎,备受推崇。那么,为什么Golang如此火爆?本文将探讨Golang之火爆原…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...