【算法】算法题-20231116
这里写目录标题
- 一、合并两个有序数组(力扣88 )
- 二、剑指 Offer 39. 数组中出现次数超过一半的数字
- 三、移除元素(力扣27)
- 四、找出字符串中第一个匹配项的下标(28)
一、合并两个有序数组(力扣88 )
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
def merge(nums1,m,nums2,n):p=0q=0if len(nums1)==0:nums1[:]=nums2[:]else:result=[0]*(m+n)for i in range(m+n):if nums1[i]<=nums2[i]:p+=1elif nums1[i]>nums2[i]:nums1[i]=nums2[i]p+=1if p==m and p!=n:result[i+1:]=nums1[q:]if p!=m and p==n:result[i+1:]=nums1[p:m]if p==m or q==n:break二、剑指 Offer 39. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2
思路:既然数组中一定有一个数占比超过总数的一半,那么当数组中的数排序后,正中间的数一定有它。。
def test(nums):nums.sort()return nums[len(nums)//2]
nums=[1, 2, 3, 2, 2, 2, 5, 4, 2]
r=test(nums)
print(r)
三、移除元素(力扣27)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/remove-element
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
def test1(nums,val):slow=0fast=0while fast<len(nums):if nums[fast]!=val:nums[slow]=nums[fast]slow+=1fast+=1return slownums=[3,2,2,3]
val=3
print(test1(nums, val))
四、找出字符串中第一个匹配项的下标(28)
给你两个字符串 haystack 和 needle ,
请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。
如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = “sadbutsad”, needle = “sad”
输出:0
解释:“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = “leetcode”, needle = “leeto”
输出:-1
解释:“leeto” 没有在 “leetcode” 中出现,所以返回 -1 。
def test6(str1,str2):str3=str1.split(str2)if len(str3)!=1:return len(str3[0])else:return -1相关文章:

【算法】算法题-20231116
这里写目录标题 一、合并两个有序数组(力扣88 )二、剑指 Offer 39. 数组中出现次数超过一半的数字三、移除元素(力扣27)四、找出字符串中第一个匹配项的下标(28) 一、合并两个有序数组(力扣88 &…...
微软允许OEM对Win10不提供关闭Secure Boot
用户可能将无法在Windows 10电脑上安装其它操作系统了,微软不再要求OEM在UEFI 中提供的“关闭 Secure Boot”的选项。 微软最早是在Designed for Windows 8认证时要求OEM的产品必须支持UEFI Secure Boot。Secure Boot 被设计用来防止恶意程序悄悄潜入到引导进程。问…...

海康G5系列(armv7l) heop模式下交叉编译Qt qmqtt demo,出现moc缺少高版本GLibc问题之解决
1.编辑源 sudo vi /etc/apt/sources.list 2.添加高版本的源 deb http://th.archive.ubuntu.com/ubuntu jammy main #添加该行到文件 3.运行升级 sudo apt update sudo apt install libc6 4.strings /**/libc.so.6 |grep GLIBC_ 参考链接:version GLIBC_2.3…...

gRPC协议详解
gRPC介绍 gRPC是一个高性能、开源和通用的RPC(远程过程调用)框架,由Google发起并开发,于2015年对外发布。它基于HTTP/2协议和Protocol Buffers设计,支持多种编程语言(如C、Java、Python、Go、Ruby、C#、No…...

虹科方案 | 从概念到生产的自动驾驶软件在环(SiL)测试解决方案
来源:雅名特自动驾驶 虹科方案 | 从概念到生产的自动驾驶软件在环(SiL)测试解决方案 自动驾驶软件在环(SiL)测试解决方案 自动驾驶软件在环(SiL)测试解决方案能够研究和验证高历程实验和恶劣驾…...

demo(二)eurekaribbon----服务注册、提供与消费
前一篇实现了服务注册中心的搭建,并提供服务注册到注册中心上。在之前的基础上,实现服务消费。 一、相关介绍 1、RestTemplate工具 2、LoadBalanced注解 二、ribbon示例: 先启动eureka-service注册中心,再将eureka-client修改…...

2023年09月 Python(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
Python等级考试(1~6级)全部真题・点这里 一、单选题(共25题,每题2分,共50分) 第1题 阅读以下代码,程序输出结果正确的选项是?( ) def process_keywords(keywords_list):unique_keywords = list(set(keywords_list))...

python3.8 安装 ssl 模块 和 _ctypes 模块
这文章目录 前情提要安装 openssl-1.1.1重新编译安装 python3.8-rpath 编译选项介绍python3.8 跟 python3.10 的区别那要怎么解决这个问题呢,我想到有四种解决方案: 前情提要 我在之前给 python3.10 安装 ssl 模块后以为该步骤 “对于 python3.6、pytho…...

阿里云99元ECS云服务器老用户也能买,续费同价!
阿里云近日宣布了2023年的服务器优惠活动,令用户们振奋不已。最引人瞩目的消息是,阿里云放开了老用户的购买资格,99元服务器也可以供老用户购买,并且享受续费的99元优惠。此外,阿里云还推出了ECS经济型e实例࿰…...
如何使用内网穿透实现远程公网访问windows node.js的服务端
使用Nodejs搭建简单的web网页并实现公网访问 前言 Node.js是建立在谷歌Chrome的JavaScript引擎(V8引擎)的Web应用程序框架。 Node.js自带运行时环境可在Javascript脚本的基础上可以解释和执行(这类似于JVM的Java字节码)。这个运行时允许在浏览器以外的任何机器上执行JavaScri…...
WordPress 媒体库文件夹管理插件 FileBird v5.5.4和谐版下载
FileBird是一款WordPress 按照文件夹管理方式的插件。 拖放界面 拖放功能现已成为现代软件和网站的标配。本机拖动事件(包括仅在刀片中将文件移动到文件夹以及将文件夹移动到文件夹)极大地减少了完成任务所需的点击次数。 一流设计的文件夹树展示 我们…...
websocket学习笔记【springboot+websocket聊天室demo】
文章目录 WebSocket是什么?为什么需要WebSocket?WebSocket和Http连接的区别WebSocket的工作原理基本交互过程: Java中的WebSocket支持WebSocket的优势springboot websocket themlef 一个聊天室demopom.xmlWebSocketConfigChatControllerWebController…...
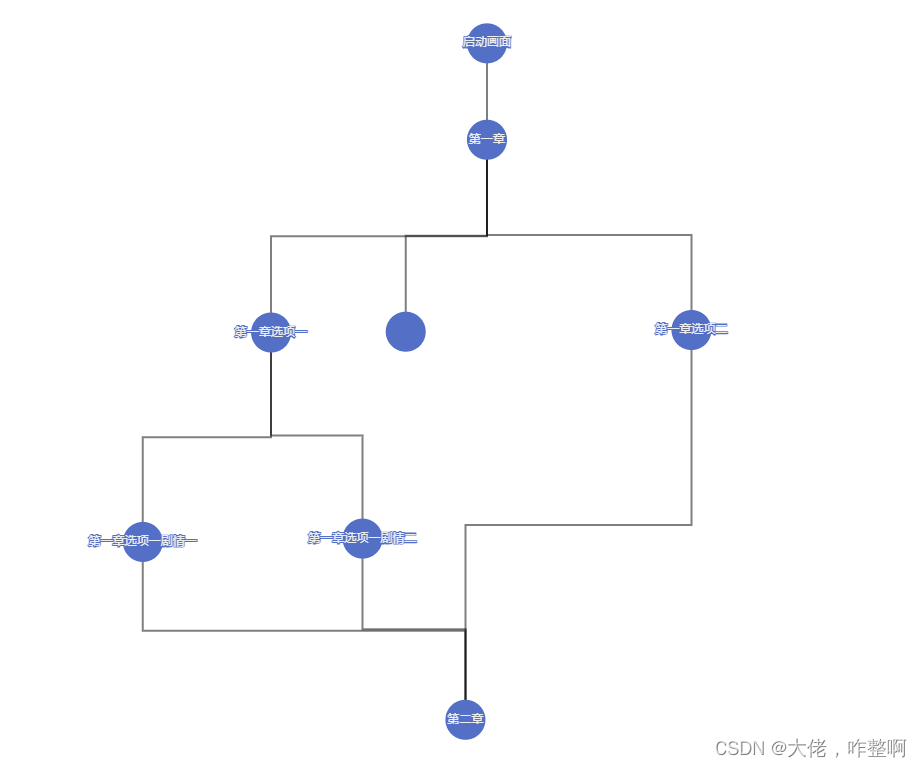
echarts:graph图表拖拽节点
需求:实现一个可视化编辑器,用户可以添加节点,并对节点进行拖拽编辑,线条要用折线而不是用自带的直线 实现期间碰到很多问题,特意记录下来,留待将来碰到这些问题的同学,省去些解决问题的时间 问…...

Unity地面交互效果目录
大家好,我是阿赵。 之前写了几篇关于地形交互、地面轨迹、脚印效果实现的博文。虽然写的篇数不多,但里面也包含了不少基础知识,比如局部UV采样、法线动态混合、曲面细分等知识,这些都是可以和别的效果组合在一起,做…...

tcp的1对多模型C++处理逻辑
连接多个设备进行TCP连接,可以采取以下策略: 创建一个设备连接管理器:使用一个类或结构体来管理每个设备的连接。这个管理器应该包含设备的IP地址和端口号,以及一个连接到该设备的TCP连接。使用并发连接:使用并发的方式同时连接到所有设备。可以使用多线程或异步编程技术来…...
)
【Python】基础(学习笔记)
一、Python介绍 1、Python优点 学习成本低 开源 适应⼈群⼴泛 应⽤领域⼴泛 2、Python解释器 Python解释器作用:运行Python文件 Python解释器分类 CPython:C语⾔开发的解释器[官⽅],应⽤⼴泛的解释器。 IPython:基于CPyth…...
)
目标检测YOLO实战应用案例100讲-基于改进YOLO v5的排水管网缺陷智能识别(续)
目录 3.3构建方法 3.3.1样本库框架 3.3.2总体流程 3.3.3图像获取 3.3.4质量控制 3.3.5数据扩增...

《AI超级个体:ChatGPT与AIGC实战指南 》书籍分享
前言 ChatGPT是一款通用人工智能(AI)工具,使用过它的人都能感受到它的魅力。AI并不是一个新事物,它在全世界都发展很多年了,但在ChatGPT诞生之前,我们的AI只能算垂直AI,比如AlphaGo,…...
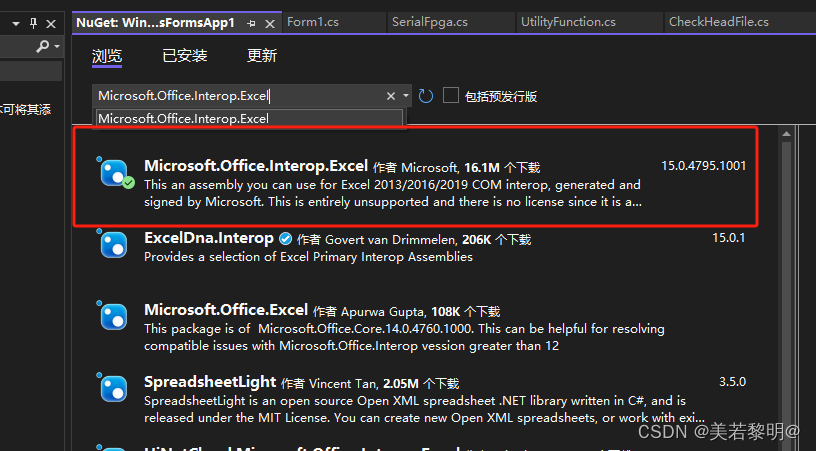
C# 使用Microsoft.Office.Interop.Excel库操作Excel
1.在NuGet管理包中搜索:Microsoft.Office.Interop.Excel,如下图红色标记处所示,进行安装 2. 安装完成后,在程序中引入命名空间如下所示: using Microsoft.Office.Interop.Excel; //第一步 添加excel第三方库 usi…...

110.42.7.1ping IP延迟代表什么意思,自己延迟高会表示其他人也高延迟吗?
我们在使用服务器前,经常会有习惯性的Ping 服务器IP看下延迟。那这个延迟是什么意思呢? ping IP延迟一般是指在网络上发送一次数据包到目标IP地址并返回的时间,通常以毫秒计算。较小的延迟表示网络连接速度较快,较大的延迟则表示…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
