2023亚太杯数学建模C题思路解析
文章目录
- 0 赛题思路
- 1 竞赛信息
- 2 竞赛时间
- 3 建模常见问题类型
- 3.1 分类问题
- 3.2 优化问题
- 3.3 预测问题
- 3.4 评价问题
- 4 建模资料
- 5 最后
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 竞赛信息
2023年第十三届亚太地区大学生数学建模竞赛(以下简称“竞赛”)是北京图象图形学学会主办的亚太地区大学生学科类竞赛,竞赛由亚太地区大学生数学建模竞赛组委会负责组织,欢迎各高等院校按照竞赛章程及有关规定组织同学报名参赛。
2022年第十二届亚太地区大学生数学建模竞赛共有9700支队伍969所高校2万7千多名学生报名参赛。参赛高校覆盖北京大学、清华大学、浙江大学、同济大学、上海交通大学、复旦大学、四川大学、大连理工大学等全部的39所985高校和114所211高校。
除中国大陆高校外,本次参赛队伍还有来自美国的加州大学伯克利分校、约翰斯霍普金斯大学、纽约大学;英国的密德萨斯大学、牛津大学、利物浦大学、诺丁汉大学、爱丁堡大学;德国的亚琛工业大学、 北黑森应用技术大学;俄罗斯的圣彼得堡国立建筑大学;澳大利亚的墨尔本大学、悉尼大学;马来西亚的马来亚大学;日本的東北大学;法国的巴黎先贤祠-阿萨斯大学;澳门地区的澳门城市大学、澳门科技大学、澳门理工学院、澳门大学;香港地区的北京师范大学-香港浸会大学联合国际学院、香港中文大学、香港科技大学、香港理工大学;中外合作的宁波诺丁汉大学、深圳北理莫斯科大学、西安交通利物浦大学等高校。
目前竞赛具有较高的国际影响力,在国内高校中是作为美赛热身赛、保研加分、综合测评加分、创新奖学金等评定竞赛之一。
2 竞赛时间
报名结束时间:2023年11月22日
比赛开始时间:2023年11月23日(周四)6:00
比赛结束时间:2023年11月27日(周一)9:00
3 建模常见问题类型
趁现在赛题还没更新,A君给大家汇总一下数学建模经常使用到的数学模型,题目八九不离十基本属于一下四种问题,对应的解法A君也相应给出
分别为:
分类模型
优化模型
预测模型
评价模型
3.1 分类问题
判别分析:
又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数;用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标;据此即可确定某一样本属于何类。当得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。
聚类分析:
聚类分析或聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
聚类分析本身不是某一种特定的算法,而是一个大体上的需要解决的任务。它可以通过不同的算法来实现,这些算法在理解集群的构成以及如何有效地找到它们等方面有很大的不同。
神经网络分类:
BP 神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。RBF(径向基)神经网络:径向基函数(RBF-Radial Basis Function)神经网络是具有单隐层的三层前馈网络。它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。感知器神经网络:是一个具有单层计算神经元的神经网络,网络的传递函数是线性阈值单元。主要用来模拟人脑的感知特征。线性神经网络:是比较简单的一种神经网络,由一个或者多个线性神经元构成。采用线性函数作为传递函数,所以输出可以是任意值。自组织神经网络:自组织神经网络包括自组织竞争网络、自组织特征映射网络、学习向量量化等网络结构形式。K近邻算法: K最近邻分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
3.2 优化问题
线性规划:
研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。它是运筹学的一个重要分支,广泛应用于生产计划、物流运输、资源分配、金融投资等领域。建模方法:列出约束条件及目标函数;画出约束条件所表示的可行域;在可行域内求目标函数的最优解及最优值。
整数规划:
规划中的变量(全部或部分)限制为整数,称为整数规划。若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性,二次和非线性的整数规划。
非线性规划:
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划研究一个 n元实函数在一组等式或不等式的约束条件下的极值问题,且 目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是 线性函数的情形则属于线性规划。
动态规划:
包括背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等。
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
多目标规划:
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。任何多目标规划问题,都由两个基本部分组成:
(1)两个以上的目标函数;
(2)若干个约束条件。有n个决策变量,k个目标函数, m个约束方程,则:
Z=F(X)是k维函数向量,Φ(X)是m维函数向量;G是m维常数向量;
3.3 预测问题
回归拟合预测
拟合预测是建立一个模型去逼近实际数据序列的过程,适用于发展性的体系。建立模型时,通常都要指定一个有明确意义的时间原点和时间单位。而且,当t趋向于无穷大时,模型应当仍然有意义。将拟合预测单独作为一类体系研究,其意义在于强调其唯“象”性。一个预测模型的建立,要尽可能符合实际体系,这是拟合的原则。拟合的程度可以用最小二乘方、最大拟然性、最小绝对偏差来衡量。
灰色预测
灰色预测是就灰色系统所做的预测。是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
马尔科夫预测:是一种可以用来进行组织的内部人力资源供给预测的方法.它的基本 思想是找出过去人事变动的 规律,以此来推测未来的人事变动趋势.转换矩阵实际上是转换概率矩阵,描述的是组织中员工流入,流出和内部流动的整体形式,可以作为预测内部劳动力供给的基础.
BP神经网络预测
BP网络(Back-ProPagation Network)又称反向传播神经网络, 通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
支持向量机法
支持向量机(SVM)也称为支持向量网络[1],是使用分类与回归分析来分析数据的监督学习模型及其相关的学习算法。在给定一组训练样本后,每个训练样本被标记为属于两个类别中的一个或另一个。支持向量机(SVM)的训练算法会创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器(尽管在概率分类设置中,存在像普拉托校正这样的方法使用支持向量机)。支持向量机模型将样本表示为在空间中的映射的点,这样具有单一类别的样本能尽可能明显的间隔分开出来。所有这样新的样本映射到同一空间,就可以基于它们落在间隔的哪一侧来预测属于哪一类别。
3.4 评价问题
层次分析法
是指将一个复杂的 多目标决策问题 作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
优劣解距离法
又称理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最大值和最小值,通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
模糊综合评价法
是一种基于模糊数学的综合评标方法。 该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。 它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色关联分析法(灰色综合评价法)
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
典型相关分析法:是对互协方差矩阵的一种理解,是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
主成分分析法(降维)
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。
因子分析法(降维)
因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
BP神经网络综合评价法
是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
4 建模资料
资料分享: 最强建模资料


5 最后
相关文章:

2023亚太杯数学建模C题思路解析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

acme在同一台服务器上设置多个Ali_key实现自动ssl申请和续期
在同一台服务器上设置多个Ali_key,您可以按照以下步骤进行操作: 首先,确保您已经安装了acme.sh工具。如果没有安装,请先安装acme.sh,您可以使用以下命令安装acme.sh: curl https://get.acme.sh | sh安装完…...

乐观锁与悲观锁
乐观锁 乐观锁是一种并发控制的机制,其核心思想是假设多个事务之间的冲突是不太可能发生的,因此在事务处理之前不会加锁,而是在事务提交的时候再检查是否有冲突。如果发现冲突,就会回滚事务,重新尝试。 实现乐观锁的方…...

【算法】堆排序
算法-堆排序 前置知识 堆(即将更新) 思路 我们现在有一个序列,怎么对它排序? 这是一个非常经典的问题,这里我们使用一个借助数据结构的算法——堆排序解决。 这里有一个序列,要对它升序排序 4 7 3 6 5 …...

51单片机应用从零开始(三)
51单片机应用从零开始(一)-CSDN博客 51单片机应用从零开始(二)-CSDN博客 详解 KEIL C51 软件的使用建立工程-CSDN博客 详解 KEIL C51 软件的使用设置工程编绎与连接程序-CSDN博客 目录 1. 用单片机控制第一个灯亮 2. 认识单片…...

如何在 Nginx Proxy Manager(NPM)上部署静态网站
前言 众所周知,我们在之前介绍过 Nginx Proxy Manager(以下简称 NPM) 这个反向代理的神器,对于一些 Docker 搭建的 Web 项目,NPM 能够很轻松地给他们做反向代理。 然而对于一些静态网站,小伙伴们可能不知道怎么用 NP…...

http的几种方法
http的几种方法在 rfc2616 中进行了定义: https://www.rfc-editor.org/rfc/rfc2616.html#page-51 HEAD方法:HEAD方法和GET方法相同,只不过服务端只返回头,不返回消息体。GET方法:用于获取资源POST方法:用于…...

var、let、const关键字的特性,以及let、const暂时性死区的作用
var、let和const都是JavaScript中的关键字,用于声明变量。 var关键字声明的变量是函数作用域或全局作用域的,它在整个函数或全局范围内都是可用的。var没有块级作用域。 let关键字声明的变量是块级作用域的,它只在包含它的代码块中可用。le…...
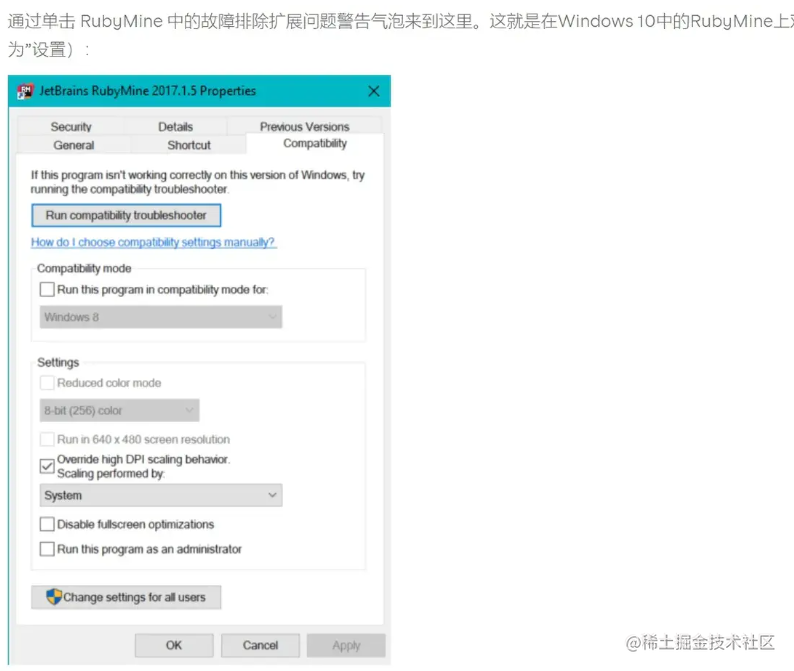
IDEA 高分辨率卡顿优化
VM设置优化 -Dsun.java2d.uiScale.enabledfalse 增加该条设置,关闭高分切换 https://intellij-support.jetbrains.com/hc/en-us/articles/115001260010-Troubleshooting-IDE-scaling-DPI-issues-on-Windowsintellij-support.jetbrains.com/hc/en-us/articles/1…...

【AIGC】一起学习prompt提示词(4/4)【经典】【15种提示词技巧】
写的时候并没有设计好,要做多少期,还是有始有终的比较好,为了方便阅读,我把之前的3期,改下名字,放到这里。 【AIGC】一起学习prompt提示词(1/4) 内容摘要:提示词是什么…...

Linux实战一天一个小指令--《文件管理/文件查找》
阿丹: 作为一个java程序员进行实战开发不接触linux操作系统基本上是不可能的,所以这个专题就出现了,本文章重点解决大家关于文件管理以及文件查找查看的疑惑。我将采用语法基础用法并在下面进行高级语法的总结使用,方便大家学习和…...
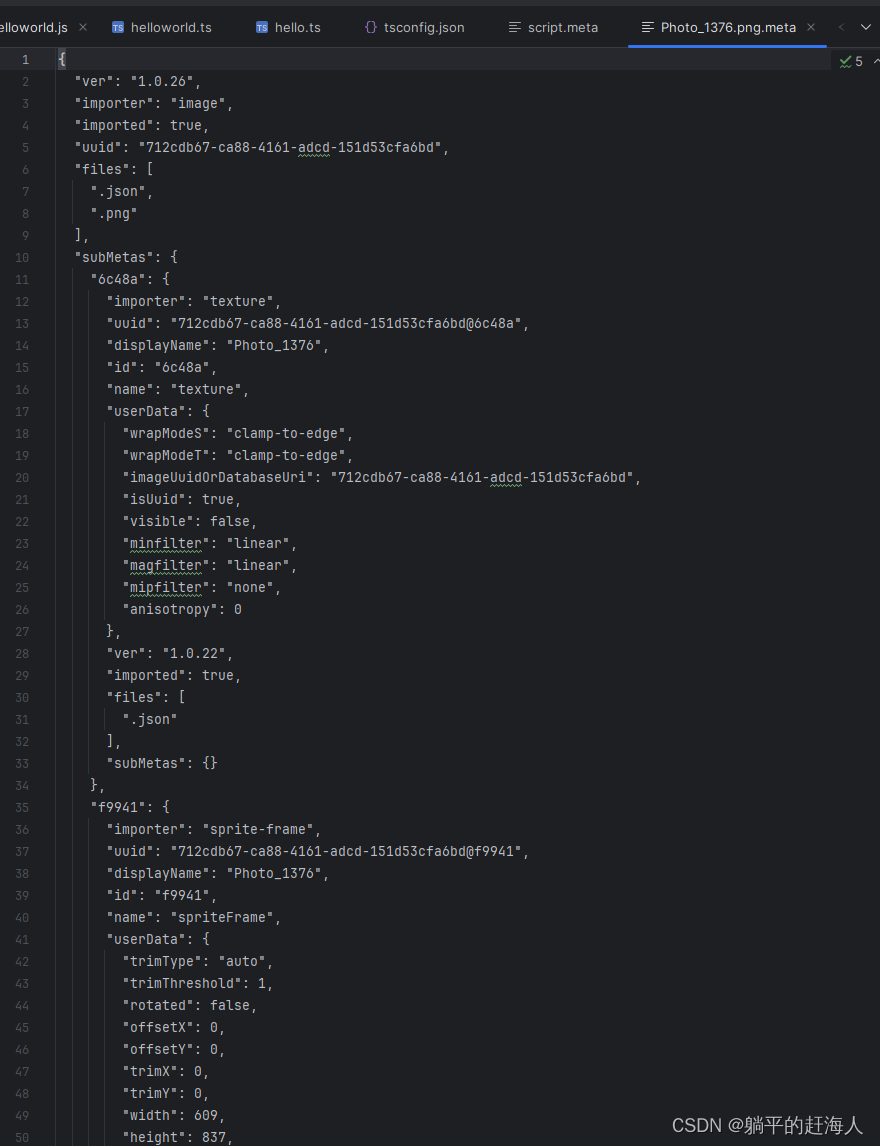
CocosCreator3.8神秘面纱 CocosCreator 项目结构说明及编辑器的简单使用
我们通过Dashboard 创建一个2d项目,来演示CocosCreator 的项目结构。 等待创建完成后,会得到以下项目工程: 一、assets文件夹 assets文件夹:为资源目录,用来存储所有的本地资源,如各种图片,脚本…...
JJJ:python学习笔记
p4 没有编译的过程 源码和输入得到输出 静态语言:编译型 脚本语言:解释型 p5 又叫做胶水语言 p7 p8 p10...

SpringSecurity6从入门到上天系列第七篇:讲明白SpringBoot的自动装配完善上篇文章中的结论
文章目录 一:SpringBoot的自动装配 1:从run方法到入口类内容被注册到注解解读器中。 2:解析入口类注解到加载Bean实例 大神链接:作者有幸结识技术大神孙哥为好友,获益匪浅。现在把孙哥视频分享给大家。 孙哥链接&am…...

ClickHouse 原理解析之基础知识总结
ClickHouse 基础知识整理 参考ClickHouse 官方文档:https://clickhouse.com/docs/en/intro 一:行式存储和列式存储 1.行式存储和列式存储的区别 1.1 概念说明 行式存储:指存储结构化数据时,在底层的存储介质上,数据是以行的方式来组织的,即存储完一条记录的所有字段,再…...

最小花费——最短路
在 n 个人中,某些人的银行账号之间可以互相转账。这些人之间转账的手续费各不相同。给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问 A 最少需要多少钱使得转账后 B 收到 100 元。 输入格式 第一行输入两个正整数 n,m,分别表…...

Spark DataFrame join后移除重复的列
在Spark,两个DataFrame做join操作后,会出现重复的列。例如: Dataset<Row> moviesWithRating moviesDF.join(averageRatingMoviesDF,moviesDF.col("movieId").equalTo(averageRatingMoviesDF.col("movieId")));其s…...

NextJS工程部署到阿里云linux Ecs
nextjs项目有多种部署方式,本文介绍最简单的一种方式,将源码上传到云服务器,编译后使用pm2后台运行nextjs工程。 检查node、npm是否安装 查看npm版本,如果版本较低先升级npm版本 npm -v卸载 yum remove nodejs npm -y安装新版…...

汽车以太网IOP测试新利器
IOP测试目的 汽车以太网物理层IOP(Interoperability )测试,即测试被测对象以太网物理层之间的互操作性。用于验证车载以太网PHY能否在有限时间内建立稳定的链路;此外,还用于验证车载以太网PHY可靠性相关的诊断特性&am…...

高防IP是什么?如何隐藏源站IP?如何进行防护?
高防IP是针对互联网服务器遭受大流量的DDoS攻击后导致服务不可用的情况下,推出的付费增值服务。用户在数据不转移的情况下,就可以通过配置高防IP , 将攻击流量引流到高防|P,确保源站的稳定可靠。高防IP采用的技术手段包括DDoS防护、WAF ( Web应用程序防火墙)等,它能够有效抵御来…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
