周赛370(模拟、树形DP(正难则反)、树状数组优化DP)
文章目录
- 周赛370
- [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/)
- 模拟
- [2924. 找到冠军 II](https://leetcode.cn/problems/find-champion-ii/)
- 统计入度
- [2925. 在树上执行操作以后得到的最大分数](https://leetcode.cn/problems/maximum-score-after-applying-operations-on-a-tree/)
- 正难则反 + 树形DP
- [2926. 平衡子序列的最大和](https://leetcode.cn/problems/maximum-balanced-subsequence-sum/)
- 树状数组优化DP
周赛370
2923. 找到冠军 I
简单
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。
给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j :如果 grid[i][j] == 1,那么 i 队比 j 队 强 ;否则,j 队比 i 队 强 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
返回这场比赛中将会成为冠军的队伍。
示例 1:
输入:grid = [[0,1],[0,0]]
输出:0
解释:比赛中有两支队伍。
grid[0][1] == 1 表示 0 队比 1 队强。所以 0 队是冠军。
示例 2:
输入:grid = [[0,0,1],[1,0,1],[0,0,0]]
输出:1
解释:比赛中有三支队伍。
grid[1][0] == 1 表示 1 队比 0 队强。
grid[1][2] == 1 表示 1 队比 2 队强。
所以 1 队是冠军。
提示:
n == grid.lengthn == grid[i].length2 <= n <= 100grid[i][j]的值为0或1- 对于满足
i != j的所有i, j,grid[i][j] != grid[j][i]均成立 - 生成的输入满足:如果
a队比b队强,b队比c队强,那么a队比c队强
模拟
class Solution {/**本质是某一行 i 除了 g[i][i] 其他都为 1*/public int findChampion(int[][] grid) {int n = grid.length;for(int i = 0; i < n; i++){boolean winner = true;for(int j = 0; j < n; j++){if(i == j) continue;if(grid[i][j] == 0){winner = false;break;}}if(winner) return i;}return -1;}
}
2924. 找到冠军 II
中等
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。每支队伍也是 有向无环图(DAG) 上的一个节点。
给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图,其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。
从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ,也就是 b 队比 a 队 弱 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
如果这场比赛存在 唯一 一个冠军,则返回将会成为冠军的队伍。否则,返回 -1 。
注意
- 环 是形如
a1, a2, ..., an, an+1的一个序列,且满足:节点a1与节点an+1是同一个节点;节点a1, a2, ..., an互不相同;对于范围[1, n]中的每个i,均存在一条从节点ai到节点ai+1的有向边。 - 有向无环图 是不存在任何环的有向图。
示例 1:
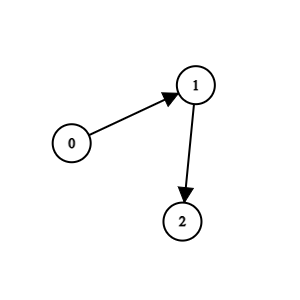
输入:n = 3, edges = [[0,1],[1,2]]
输出:0
解释:1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。
示例 2:
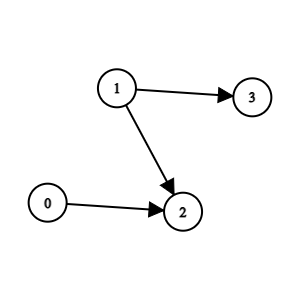
输入:n = 4, edges = [[0,2],[1,3],[1,2]]
输出:-1
解释:2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。
提示:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]- 生成的输入满足:如果
a队比b队强,就不存在b队比a队强 - 生成的输入满足:如果
a队比b队强,b队比c队强,那么a队比c队强
统计入度
class Solution {public int findChampion(int n, int[][] edges) {List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());int[] deg = new int[n];for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);deg[y] += 1;}int res = -1, cnt = 0;for(int i = 0; i < n; i++){if(deg[i] == 0){cnt += 1;res = i;}}return cnt == 1 ? res : -1;}
}
2925. 在树上执行操作以后得到的最大分数
中等
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 ,根节点编号为 0 。给你一个长度为 n - 1 的二维整数数组 edges 表示这棵树,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个长度为 n 下标从 0 开始的整数数组 values ,其中 values[i] 表示第 i 个节点的值。
一开始你的分数为 0 ,每次操作中,你将执行:
- 选择节点
i。 - 将
values[i]加入你的分数。 - 将
values[i]变为0。
如果从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0 ,那么我们称这棵树是 健康的 。
你可以对这棵树执行任意次操作,但要求执行完所有操作以后树是 健康的 ,请你返回你可以获得的 最大分数 。
示例 1:

输入:edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1]
输出:11
解释:我们可以选择节点 1 ,2 ,3 ,4 和 5 。根节点的值是非 0 的。所以从根出发到任意叶子节点路径上节点值之和都不为 0 。所以树是健康的。你的得分之和为 values[1] + values[2] + values[3] + values[4] + values[5] = 11 。
11 是你对树执行任意次操作以后可以获得的最大得分之和。
示例 2:
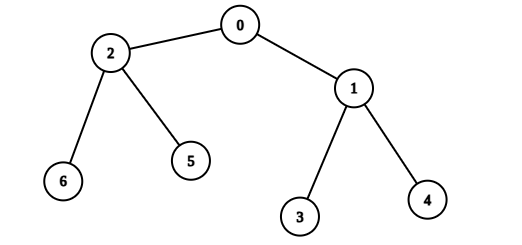
输入:edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [20,10,9,7,4,3,5]
输出:40
解释:我们选择节点 0 ,2 ,3 和 4 。
- 从 0 到 4 的节点值之和为 10 。
- 从 0 到 3 的节点值之和为 10 。
- 从 0 到 5 的节点值之和为 3 。
- 从 0 到 6 的节点值之和为 5 。
所以树是健康的。你的得分之和为 values[0] + values[2] + values[3] + values[4] = 40 。
40 是你对树执行任意次操作以后可以获得的最大得分之和。
提示:
2 <= n <= 2 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < nvalues.length == n1 <= values[i] <= 109- 输入保证
edges构成一棵合法的树。
正难则反 + 树形DP
https://leetcode.cn/problems/maximum-score-after-applying-operations-on-a-tree/solutions/2513101/shu-xing-dpxuan-huo-bu-xuan-pythonjavacg-7aj6/
class Solution {/**正难则反,先把所有数都选上,加入到答案中,然后考虑不选哪些点权对于一棵以 x 的根的子树,如果这棵树是健康的,损失的最小分数是多少选或不选不选 损失根节点的情况下,损失的最小分数 = values[x]选 不损失根节点(根节点加到答案种) = sum(dfs(y))两种情况去最小值*/public long maximumScoreAfterOperations(int[][] edges, int[] values) {List<Integer>[] g = new ArrayList[values.length];Arrays.setAll(g, e -> new ArrayList<>());g[0].add(-1); // 避免误把根节点当成叶子for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x);}// 先把所有分数加入答案long ans = 0;for(int v : values) ans += v;return ans - dfs(0, -1, g, values);}// dfs(x) 计算以 x 为根的子树是健康时,失去的最小分数public long dfs(int x, int fa, List<Integer>[] g, int[] values){if(g[x].size() == 1){ // x 是叶子return values[x];}long loss = 0; // 第二种情况for(int y : g[x]){if(y != fa){loss += dfs(y, x, g, values);}}return Math.min(values[x], loss); // 两种情况取最小值}
}
2926. 平衡子序列的最大和
困难
给你一个下标从 0 开始的整数数组 nums 。
nums 一个长度为 k 的 子序列 指的是选出 k 个 下标 i0 < i1 < ... < ik-1 ,如果这个子序列满足以下条件,我们说它是 平衡的 :
- 对于范围
[1, k - 1]内的所有j,nums[ij] - nums[ij-1] >= ij - ij-1都成立。
nums 长度为 1 的 子序列 是平衡的。
请你返回一个整数,表示 nums 平衡 子序列里面的 最大元素和 。
一个数组的 子序列 指的是从原数组中删除一些元素(也可能一个元素也不删除)后,剩余元素保持相对顺序得到的 非空 新数组。
示例 1:
输入:nums = [3,3,5,6]
输出:14
解释:这个例子中,选择子序列 [3,5,6] ,下标为 0 ,2 和 3 的元素被选中。
nums[2] - nums[0] >= 2 - 0 。
nums[3] - nums[2] >= 3 - 2 。
所以,这是一个平衡子序列,且它的和是所有平衡子序列里最大的。
包含下标 1 ,2 和 3 的子序列也是一个平衡的子序列。
最大平衡子序列和为 14 。
示例 2:
输入:nums = [5,-1,-3,8]
输出:13
解释:这个例子中,选择子序列 [5,8] ,下标为 0 和 3 的元素被选中。
nums[3] - nums[0] >= 3 - 0 。
所以,这是一个平衡子序列,且它的和是所有平衡子序列里最大的。
最大平衡子序列和为 13 。
示例 3:
输入:nums = [-2,-1]
输出:-1
解释:这个例子中,选择子序列 [-1] 。
这是一个平衡子序列,而且它的和是 nums 所有平衡子序列里最大的。
提示:
1 <= nums.length <= 105-109 <= nums[i] <= 109
树状数组优化DP
https://leetcode.cn/problems/maximum-balanced-subsequence-sum/solutions/2513121/shu-zhuang-shu-zu-you-hua-dp-by-endlessc-3zf4/
class Solution {/**思考过程nums[ij] - nums[ij-1] >= ij - ij-1nums[i] - nums[j] >= i - j==> nums[i] - i >= nums[j] - j定义 b[i] = nums[i] - ib[i] >= b[j] ==> 从 b 中选一个子序列,满足这个子序列是一个非递减的序列求对应的元素和的最大值a 3 3 5 6b 3 2 4 3定义 f[i] = 以下标 i 结尾的子序列,对应的 nums 的元素和的最大值转移 f[i] = f[j] + nums[i], j < i && b[j] <= b[i]使用值域树状数组优化,用来维护前缀最大值,设下标为x=b[i],维护的值为max(f[x], f[x-1], f[x-2]..)实现时,需要先把nums[i] - i离散化*/public long maxBalancedSubsequenceSum(int[] nums) {int n = nums.length;int[] b = new int[n];for(int i = 0; i < n; i++){b[i] = nums[i] - i;}Arrays.sort(b);BIT t = new BIT(b.length+1);for(int i = 0; i < n; i++){// j 为 nums[i]-i 离散化后的值(从 1 开始)int j = Arrays.binarySearch(b, nums[i] - i) + 1;long f = Math.max(t.preMax(j), 0) + nums[i];t.update(j, f);}return t.preMax(b.length);}
}// 树状数组模板(维护前缀最大值)
class BIT {private long[] tree;public BIT(int n) {tree = new long[n];Arrays.fill(tree, Long.MIN_VALUE);}public void update(int i, long val) {while (i < tree.length) {tree[i] = Math.max(tree[i], val);i += i & -i;}}public long preMax(int i) {long res = Long.MIN_VALUE;while (i > 0) {res = Math.max(res, tree[i]);i &= i - 1;}return res;}
}
相关文章:

周赛370(模拟、树形DP(正难则反)、树状数组优化DP)
文章目录 周赛370[2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/)模拟 [2924. 找到冠军 II](https://leetcode.cn/problems/find-champion-ii/)统计入度 [2925. 在树上执行操作以后得到的最大分数](https://leetcode.cn/problems/maximum-score-after-appl…...
python实现一个简单的桌面倒计时小程序
本章内容主要是利用python制作一个简单的桌面倒计时程序,包含开始、重置 、设置功能。 目录 一、效果演示 二、程序代码 一、效果演示 二、程序代码 #!/usr/bin/python # -*- coding: UTF-8 -*- """ author: Roc-xb """import tkin…...
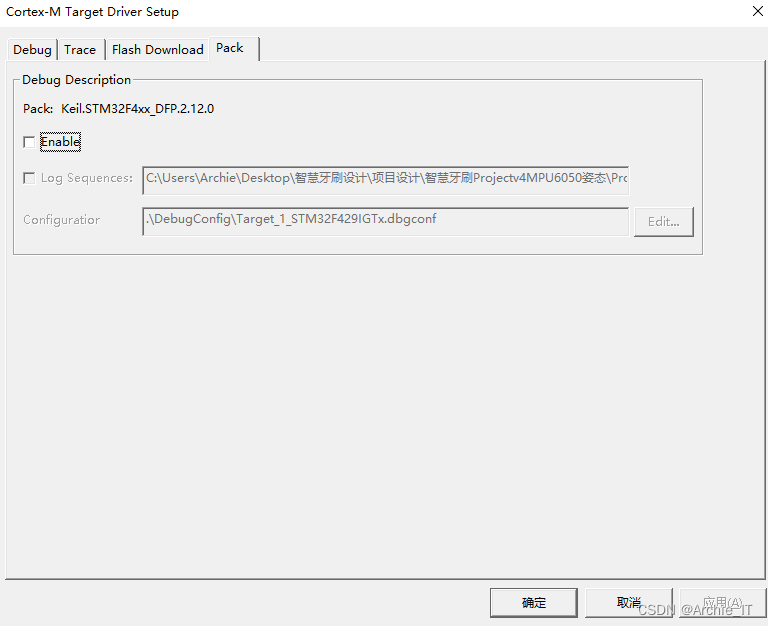
解决STM32F429烧录程序后还需复位才能植入程序的bug
1.打开魔术棒,打开debug 2.打开setting 3.打开Flas Download 4.开启Reset and Run 5.点进去Pack选项页面,去掉enable...

使用Golang调用摄像头
近年来,摄像头成为了我们生活中不可或缺的设备之一。从智能手机到安全监控系统,无处不在的摄像头给我们带来了便利和安全。在开发摄像头相关的应用程序时,选择一种高效和易用的编程语言是非常重要的。本文将介绍如何使用Golang调用摄像头并进…...
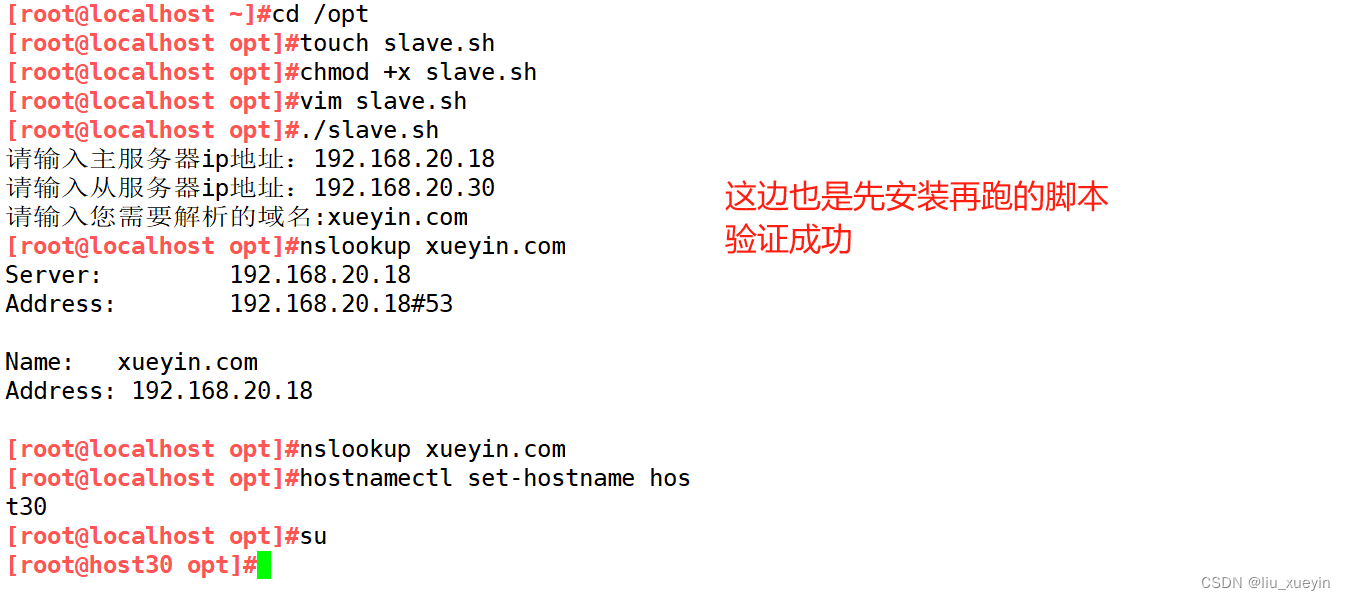
【Linux网络】1分钟使用shell脚本完成DNS主从解析服务器部署(适用于centos主机)
DNS正向解析主从解析服务器脚本 1、脚本内容 主服务器脚本 #!/bin/bash ##先修改本地DNS缓存服务器 read -p "请输入主服务器ip地址:" masterIP sed -i /DNS/d /etc/sysconfig/network-scripts/ifcfg-ens33 echo "DNS$masterIP" >> /e…...
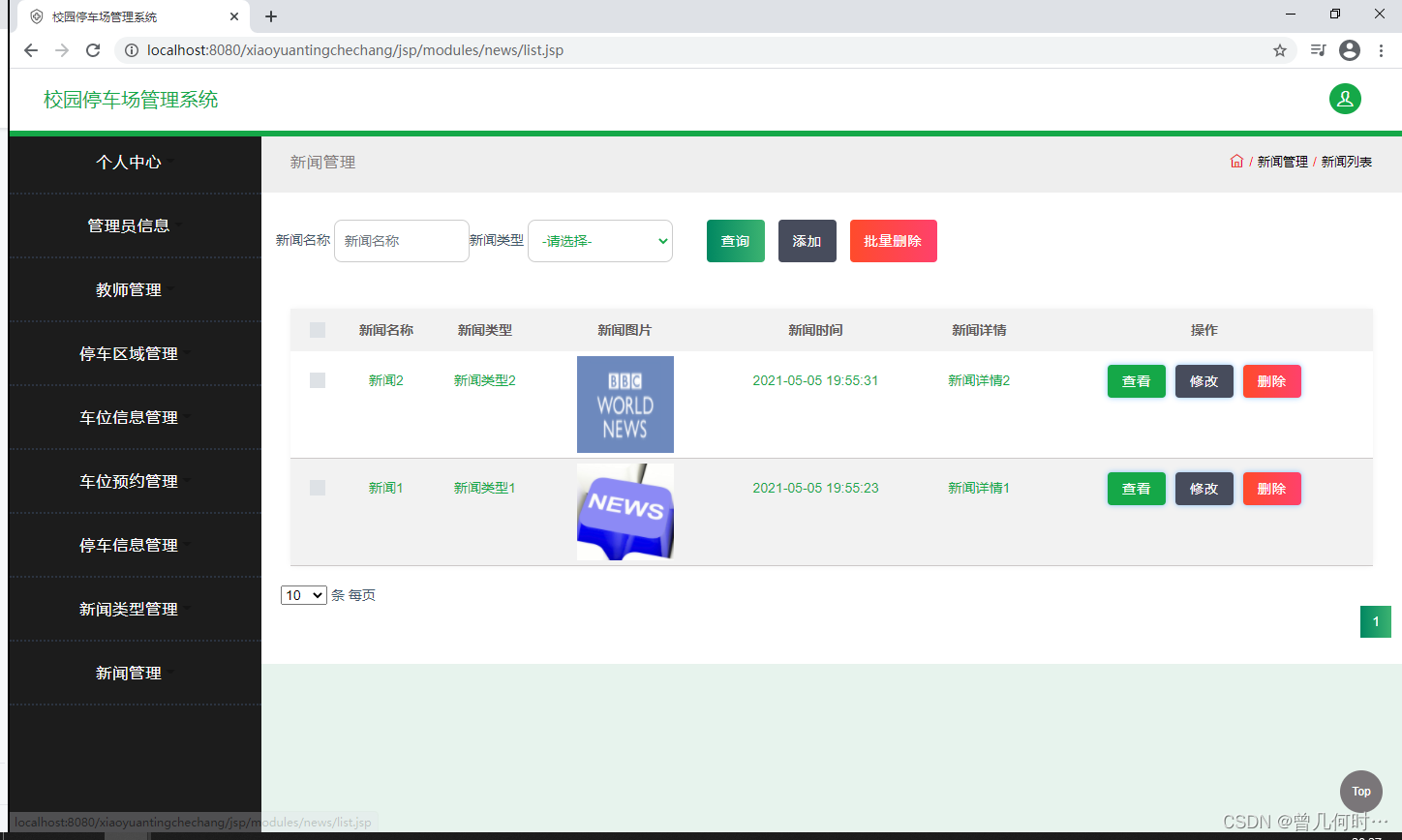
基于SSM的校园停车场管理系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
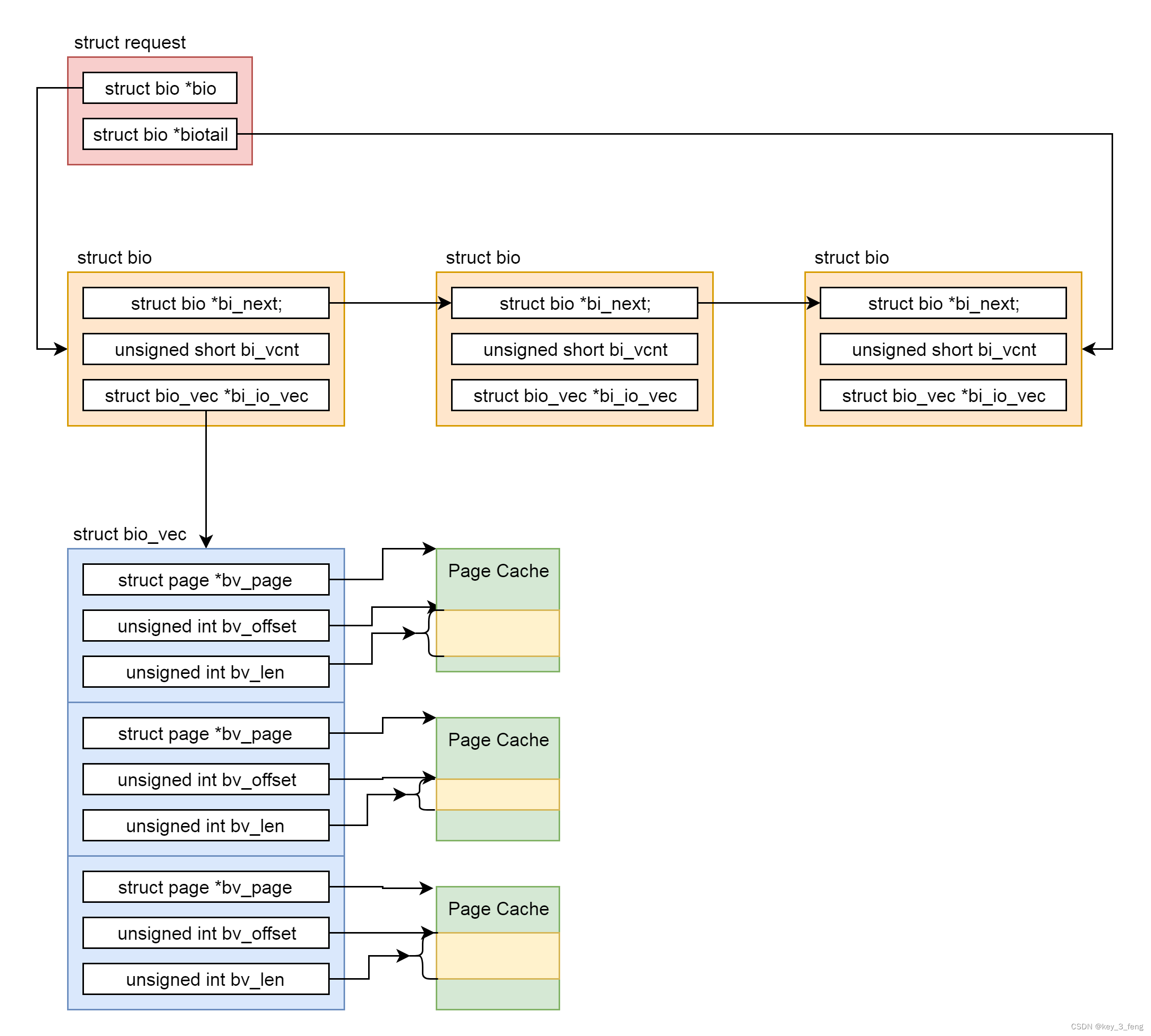
块设备 I/O 请求送达到外部设备
对于 ext4 文件系统,最后调用的是 ext4_file_write_iter,它将 I/O 的调用分成两种情况: 第一是直接 I/O。最终我们调用的是 generic_file_direct_write,这里调用的是 mapping->a_ops->direct_IO,实际调用的是 e…...
【ArcGIS Pro二次开发】(76):面积平差工具
之前做过一个【三调土地利用现状分类面积汇总】的工具,在流程中使用了面积平差的方法。 考虑了在其它场合可能也需要进行面积平差,因此单独提取出来作为一个工具。 平差实现的方法如下图: 主要的计算过程如上图所示,算出总面积差…...
4、智能家居框架设计和代码文件工程建立
目录 一、智能家居项目框架 二、智能家居工厂模式示意 三、代码文件工程建立 SourceInsight创建新工程步骤 一、智能家居项目框架 二、智能家居工厂模式示意 三、代码文件工程建立 创建一个名为si的文件夹用于保存SourceInsight生成的文件信息,然后在SourceInsig…...
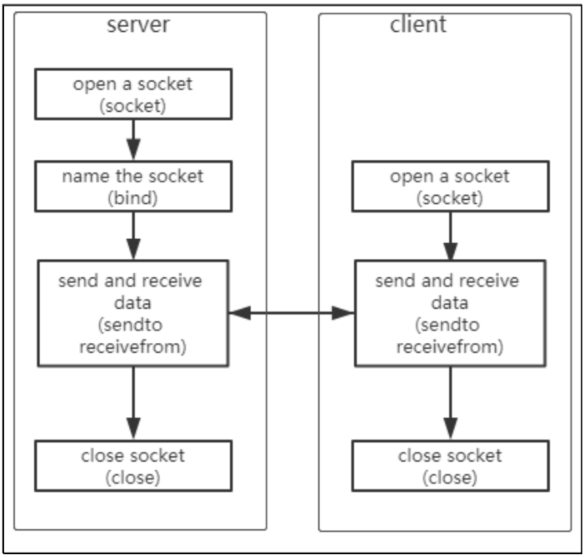
网络编程TCP/UDP
1 网络通信概述 1.1 IP 和端口 所有的数据传输,都有三个要素 :源、目的、长度。 怎么表示源或者目的呢?请看图 所以,在网络传输中需要使用“IP 和端口”来表示源或目的。 1.2 网络传输中的 2 个对象:server 和 clie…...
移远EC600U-CN开发板 11.15
制作一个简单UI: 1."端口设置"模块 *效果图 *代码 def backEvent(evt): #返回主界面code evt.get_code() if code lv.EVENT.CLICKED:lv.scr_load(mainInterface)def popUpEvent(evt): #弹窗提醒code evt.get_code()if code lv.EVENT.CL…...

Docker - MySQL Database is uninitialized and password option is not specified
问题描述 docker run --namemaster -p 3306:3306 -d mysql 2022-11-11 08:03:0500:00 [Note] [Entrypoint]: Entrypoint script for MySQL Server 8.0.31-1.el8 started. 2022-11-11 08:03:0500:00 [Note] [Entrypoint]: Switching to dedicated user mysql 2022-11-11 08:03…...

Elasticsearch 之聚合分析
本文主要介绍 Elasticsearch 的聚合功能,介绍什么是 Bucket 和 Metric 聚合,以及如何实现嵌套的聚合。 首先来看下聚合(Aggregation): 1 什么是 Aggregation? 首先举一个生活中的例子,这个是京…...

Django(七、模型层)
文章目录 模型层模型层前期准备使用django ORM要注意 代码演示:切换MySQL数据库如何查看django ORM 底层原理? 单表操作模型层之ORM常见关键字基础的增删改查常用的关键字 常见的十几种查询基于双下滑线的查询 模型层 模型层前期准备 使用django ORM要…...

LeetCode105. Construct Binary Tree from Preorder and Inorder Traversal
文章目录 一、题目二、题解 一、题目 Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree. Example 1: Input: pre…...

python链表_递归求和_递归求最大小值
创建一个单链表: class LinkNode: #设置属性def __init__(self,data None):self.data dataself.next None class LinkList: #设置头结点def __init__(self):self.head LinkNode()self.head.next Nonedef CreateListR(self,a): …...

Java中生成指定字体的印章
文章目录 1.引入字体2.Windows环境下3. Linux环境下 生成印章测试类绘制方章测试类 1.引入字体 2.Windows环境下 如果在Windows上安装JAVA环境时,没有安装单独的jre1.8.0_141的话。那么字体就只放到\jdk1.8.0_141\jre\lib\fonts目前下。 3. Linux环境下 cat /etc…...
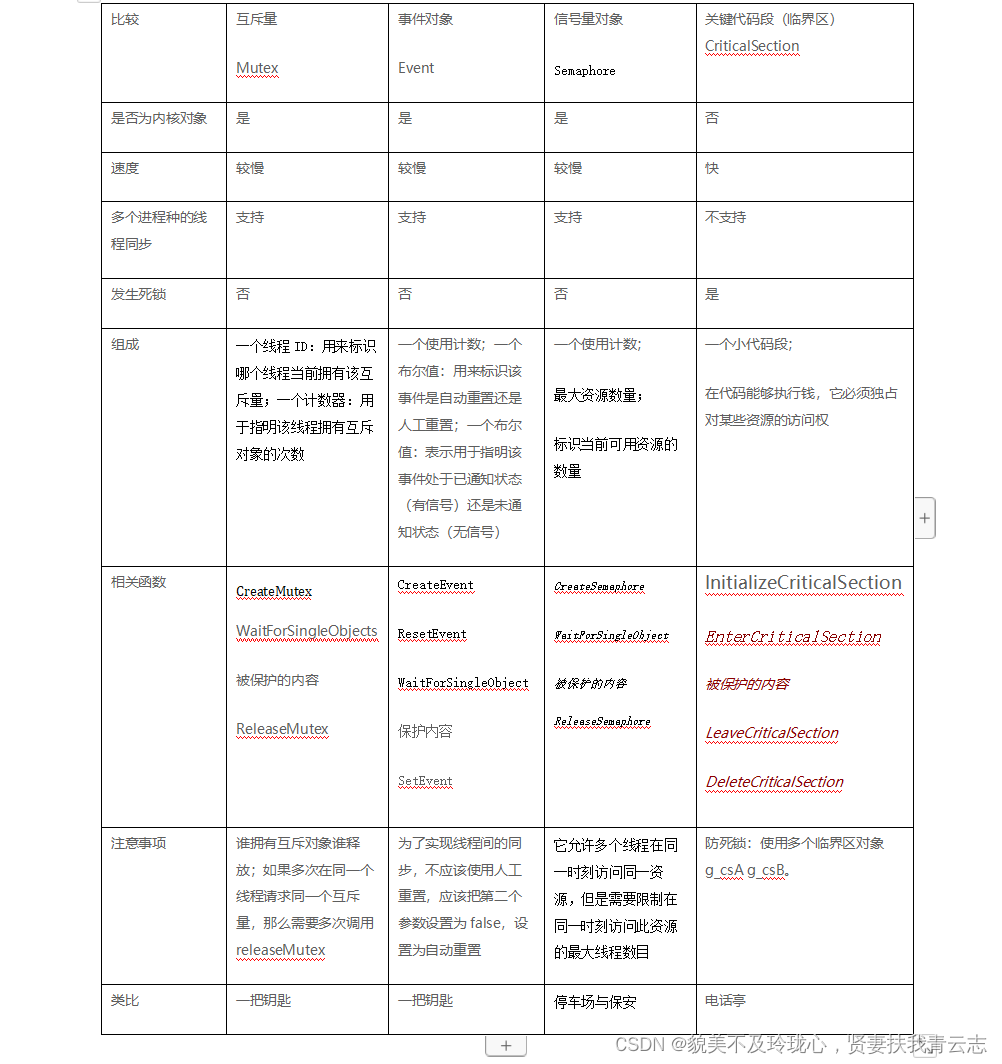
Winodws核心编程 多线程
目录 一、基本概念 二、线程创建函数 三、Windows内核对象与句柄 四、简单的多线程案例 五、线程同步 - 互斥对象 六、多线程实现群聊的服务端和客户端 七、线程同步 - 事件对象 八、事件对象 与 互斥对象区别 九、线程同步 - 信号量 十、线程同步 - 关键代码段 十一…...
旺店通·企业版对接打通金蝶云星空查询调拨单接口与分布式调入单新增接口
旺店通企业版对接打通金蝶云星空查询调拨单接口与分布式调入单新增接口 源系统:旺店通企业版 旺店通是北京掌上先机网络科技有限公司旗下品牌,国内的零售云服务提供商,基于云计算SaaS服务模式,以体系化解决方案,助力零售企业数字化…...

关于对Java中volatile关键字的理解与简述
【版权声明】未经博主同意,谢绝转载!(请尊重原创,博主保留追究权) https://blog.csdn.net/m0_69908381/article/details/134430096 出自【进步*于辰的博客】 启发之作:Java volatile关键字最全总结…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
