【数据结构高阶】二叉搜索树
接下来我们来开始使用C++来详细讲解数据结构的一些高阶的知识点
本期讲解的是二叉搜索树,对于初阶二叉树有所遗忘的同学可以看到这里:
【精选】【数据结构初阶】链式二叉树的解析及一些基本操作
讲解二叉搜索树主要是为了后面的map和set做铺垫,废话不多说我们直接上干货:
目录
一、二叉搜索树的概念
二、模拟实现二叉搜索树
2.1 插入数据
2.1.1 插入数据的非递归实现
2.2 遍历数据
2.3 查找数据
2.4 删除数据
2.4.1 删除数据的非递归实现
2.5 模拟实现二叉搜索树的全部代码
一、二叉搜索树的概念
二叉搜索树又称二叉排序树(BST, Binary Search Tree),它可以是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
例如:
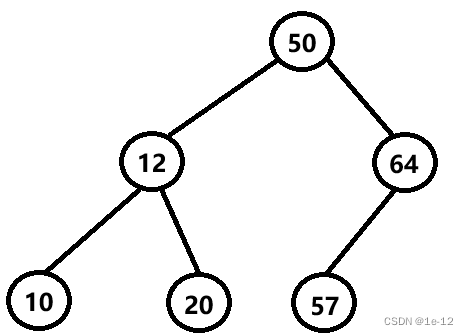
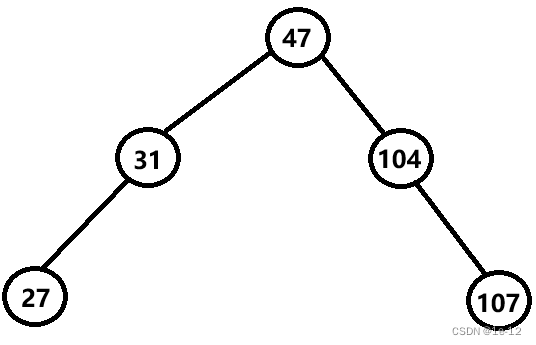
我们可以发现的一点:无论是什么样的二叉搜索树,使用中序遍历,遍历出的值都是升序排列的
二、模拟实现二叉搜索树
下面又到了我们最激动人心的代码实现环节,本次代码实现我们还是要基于链式二叉树的实现:
template<class K>
struct BSTreeNode//节点
{BSTreeNode<K>* _lchild;BSTreeNode<K>* _rchild;K _key;BSTreeNode(const K& key):_lchild(nullptr),_rchild(nullptr),_key(key){}
};
2.1 插入数据
我们可以根据二叉搜索树的规律来向其中插入数据,但是插入数据时需要注意一点:要记录插入节点的上一个父节点,将插入的节点连接上二叉树:
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);_root->_key = key;return true;}Node* cur = _root;//使用cur遍历二叉树找到合适的插入位置Node* parent = cur;//记录cur的父节点while (cur){parent = cur;if (key < cur->_key){cur = cur->_lchild;}else if (key > cur->_key){cur = cur->_rchild;}else{return false;//这里创建的二叉搜索树不允许出现值的冗余}}cur = new Node(key);//创建//将创建的节点链接到二叉树上if (key < parent->_key){parent->_lchild = cur;}else{parent->_rchild = cur;}return true;}private:Node* _root = nullptr;//根节点
};2.1.1 插入数据的非递归实现
递归的效率并没有循环高,那为什么要说一下插入数据的非递归实现呢
主要是非递归的数据插入的传值方法值得一说:
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool InsertR(const K& key)//插入数据(递归){return _InsertR(_root, key);}bool _InsertR(Node*& root,const K& key)//这里使用指针的引用用来直接修改其父节点指针的指向{if (root == nullptr){root = new Node(key);return true;}if (root->_key > key){_InsertR(root->_lchild, key);}else if (root->_key < key){_InsertR(root->_rchild, key);}else{return false;}}
private:Node* _root = nullptr;//根节点
};我们可以看到在递归时,传入的形参类型为Node*&,这样可以直接在其函数内部习惯其父节点孩子指针的指向
那为什么要写两个插入函数呢?因为如果我们直接使用_InsertR函数,无法直接使用对象对_InsertR函数进行传参
2.2 遍历数据
因为二叉搜索树的性质,这里我们采用中序遍历:
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key)插入数据{....}void InOrder()//中序遍历{_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == NULL)//如果是空树就直接结束{return;}_InOrder(root->_lchild);//先递归遍历其左子树cout << root->_key << " ";//再遍历其根节点_InOrder(root->_rchild);//最后递归遍历其右子树}private:Node* _root = nullptr;//根节点
};那为什么要写两个中序遍历函数呢?因为如果我们直接使用_InOrder函数,无法直接使用对象对_InOrder函数进行传参
2.3 查找数据
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key)//插入数据{......}void InOrder()//中序遍历{......}void _InOrder(Node* root){......}bool Find(const K& key)//查找数据{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_rchild;}else if (cur->_key > key){cur = cur->_lchild;}else{return true;}}return false;}private:Node* _root = nullptr;//根节点
};2.4 删除数据
对于在二叉搜索树中删除数据,我们就要好好说道说道了
下面我们有这样的一个二叉搜索树:

现在我们要删除其叶子节点,这很容易,直接删除完,再将其父节点对应的孩子指针置空即可
那我们要删只有一个孩子节点的数据呢?例如14和10
这个稍微麻烦一点,删除完该节点后将其孩子节点托付给其父节点即可:

那要删带有两个孩子节点的数据呢?例如3、6、8:
对于这种情况我们可以选择其节点下的左子树的最大节点(左子树的最右节点),或者右子树的最小节点(右子树的最左节点)来替代要删除的节点:

综上所述,要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
思路我们有了,下面用代码来实现一下:
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key)//插入数据{...}void InOrder()//中序遍历{...}private:void _InOrder(Node* root){...}public:bool Find(const K& key)//查找数据{...}bool Erase(const K& key){Node* cur = _root;//使用cur遍历二叉树找到要删除元素的位置Node* parent = cur;//记录cur的父节点while (cur)//寻找需要删除的节点{if (cur->_key < key){parent = cur;cur = cur->_rchild;}else if (cur->_key > key){parent = cur;cur = cur->_lchild;}else//找到了,开始删除{if (cur->_lchild == cur->_rchild && cur->_lchild == nullptr)//删除的节点为叶子节点{if (parent == cur)//删除的是根节点{_root = nullptr;//更新根节点}//将其父节点指向的自身的指针置空else if (parent->_lchild == cur){parent->_lchild = nullptr;}else{parent->_rchild = nullptr;}//释放节点空间delete cur;cur = nullptr;}else if (cur->_rchild == nullptr)//删除的节点右孩子为空,左孩子不为空{if (parent == cur)//删除的是根节点{_root = cur->_lchild;//更新根节点}//将删除节点的左孩子交给其父节点else if (parent->_lchild == cur){parent->_lchild = cur->_lchild;}else{parent->_rchild = cur->_lchild;}//释放节点空间delete cur;cur = nullptr;}else if (cur->_lchild == nullptr)//删除的节点左孩子为空,右孩子不为空{if (parent == cur)//删除的是根节点{_root = cur->_rchild;//更新根节点}//将删除节点的右孩子交给其父节点else if (parent->_lchild == cur){parent->_lchild = cur->_rchild;}else{parent->_rchild = cur->_rchild;}//释放节点空间delete cur;cur = nullptr;}else//删除的节点左右孩子都不为空,要找到删除节点的左子树的最大节点或右子树的最小节点可将其替换{//这里找要删除节点的左子树的最大节点(右子树的最小节点也可)Node* maxleft = cur->_lchild; // 记录左子树的最大节点Node* pmaxleft = cur;//记录左子树的最大节点的父节点while (maxleft->_rchild)//查找左子树的最大节点{pmaxleft = maxleft;maxleft = maxleft->_rchild;}//将找到的节点替换要删除的节点cur->_key = maxleft->_key;if (pmaxleft->_lchild == maxleft){pmaxleft->_lchild = maxleft->_lchild;}else{pmaxleft->_rchild = maxleft->_lchild;}//释放节点空间delete maxleft;maxleft = nullptr;}return true;}}return false;//没找到要删除的节点}
private:Node* _root = nullptr;//根节点
};2.4.1 删除数据的非递归实现
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool EraseR(const K& key)//递归删除数据{return _EraseR(_root, key);}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}else if (root->_key < key){_EraseR(root->_rchild, key);}else if (root->_key > key){_EraseR(root->_lchild, key);}else{Node* del = root;if (root->_lchild == root->_rchild && root->_lchild == nullptr)//删除的节点为叶子节点{//释放节点空间delete root;//将其父节点指向的自身的指针置空root = nullptr;}else if (root->_rchild == nullptr)//删除的节点右孩子为空,左孩子不为空{//将删除节点的左孩子交给其父节点root = root->_lchild;//释放节点空间delete del;del = nullptr;}else if (root->_lchild == nullptr)//删除的节点左孩子为空,右孩子不为空{//将删除节点的右孩子交给其父节点root = root->_rchild;//释放节点空间delete del;del = nullptr;}else//删除的节点左右孩子都不为空,要找到删除节点的左子树的最大节点或右子树的最小节点将其替换{//这里找要删除节点的右子树的最小节点(左子树的最大节点也可)Node* minright = del->_rchild; // 记录右子树的最小节点while (minright->_lchild)//查找右子树的最小节点{minright = minright->_lchild;}root->_key = minright->_key;//将找到的节点替换要删除的节点return _EraseR(root->_rchild, root->_key);//继续递归删除其右子树中用来替换的节点}return true;}}private:Node* _root = nullptr;//根节点
};
2.5 模拟实现二叉搜索树的全部代码
#include<iostream>
using namespace std;template<class K>
struct BSTreeNode//节点
{BSTreeNode<K>* _lchild;BSTreeNode<K>* _rchild;K _key;BSTreeNode(const K& key):_lchild(nullptr),_rchild(nullptr),_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key)//插入数据{if (_root == nullptr)//如果根节点为空就直接插入{_root = new Node(key);_root->_key = key;return true;}Node* cur = _root;//使用cur遍历二叉树找到合适的插入位置Node* parent = cur;//记录cur的父节点while (cur){parent = cur;if (key < cur->_key){cur = cur->_lchild;}else if (key > cur->_key){cur = cur->_rchild;}else{return false;//这里创建的二叉搜索树不允许出现值的冗余}}cur = new Node(key);//创建//将创建的节点链接到二叉树上if (key < parent->_key){parent->_lchild = cur;}else{parent->_rchild = cur;}return true;}bool InsertR(const K& key)//插入数据(递归){return _InsertR(_root, key);}private:bool _InsertR(Node*& root,const K& key)//这里使用指针的引用用来直接修改其父节点指针的指向{if (root == nullptr){root = new Node(key);return true;}if (root->_key > key){_InsertR(root->_lchild, key);}else if (root->_key < key){_InsertR(root->_rchild, key);}else{return false;}}public:void InOrder()//中序遍历{_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == NULL)//如果是空树就直接结束{return;}_InOrder(root->_lchild);//先递归遍历其左子树cout << root->_key << " ";//再遍历其根节点_InOrder(root->_rchild);//最后递归遍历其右子树}public:bool Find(const K& key)//查找数据{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_rchild;}else if (cur->_key > key){cur = cur->_lchild;}else{return true;}}return false;}bool Erase(const K& key)//删除数据{Node* cur = _root;//使用cur遍历二叉树找到要删除元素的位置Node* parent = cur;//记录cur的父节点while (cur)//寻找需要删除的节点{if (cur->_key < key){parent = cur;cur = cur->_rchild;}else if (cur->_key > key){parent = cur;cur = cur->_lchild;}else//找到了,开始删除{if (cur->_lchild == cur->_rchild && cur->_lchild == nullptr)//删除的节点为叶子节点{if (parent == cur)//删除的是根节点{_root = nullptr;//更新根节点}//将其父节点指向的自身的指针置空else if (parent->_lchild == cur){parent->_lchild = nullptr;}else{parent->_rchild = nullptr;}//释放节点空间delete cur;cur = nullptr;}else if (cur->_rchild == nullptr)//删除的节点右孩子为空,左孩子不为空{if (parent == cur)//删除的是根节点{_root = cur->_lchild;//更新根节点}//将删除节点的左孩子交给其父节点else if (parent->_lchild == cur){parent->_lchild = cur->_lchild;}else{parent->_rchild = cur->_lchild;}//释放节点空间delete cur;cur = nullptr;}else if (cur->_lchild == nullptr)//删除的节点左孩子为空,右孩子不为空{if (parent == cur)//删除的是根节点{_root = cur->_rchild;//更新根节点}//将删除节点的右孩子交给其父节点else if (parent->_lchild == cur){parent->_lchild = cur->_rchild;}else{parent->_rchild = cur->_rchild;}//释放节点空间delete cur;cur = nullptr;}else//删除的节点左右孩子都不为空,要找到删除节点的左子树的最大节点或右子树的最小节点可将其替换{//这里找要删除节点的左子树的最大节点(右子树的最小节点也可)Node* maxleft = cur->_lchild; // 记录左子树的最大节点Node* pmaxleft = cur;//记录左子树的最大节点的父节点while (maxleft->_rchild)//查找左子树的最大节点{pmaxleft = maxleft;maxleft = maxleft->_rchild;}//将找到的节点替换要删除的节点cur->_key = maxleft->_key;if (pmaxleft->_lchild == maxleft){pmaxleft->_lchild = maxleft->_lchild;}else{pmaxleft->_rchild = maxleft->_lchild;}//释放节点空间delete maxleft;maxleft = nullptr;}return true;}}return false;//没找到要删除的节点}bool EraseR(const K& key)//递归删除数据{return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}else if (root->_key < key){_EraseR(root->_rchild, key);}else if (root->_key > key){_EraseR(root->_lchild, key);}else{Node* del = root;if (root->_lchild == root->_rchild && root->_lchild == nullptr)//删除的节点为叶子节点{//释放节点空间delete root;//将其父节点指向的自身的指针置空root = nullptr;}else if (root->_rchild == nullptr)//删除的节点右孩子为空,左孩子不为空{//将删除节点的左孩子交给其父节点root = root->_lchild;//释放节点空间delete del;del = nullptr;}else if (root->_lchild == nullptr)//删除的节点左孩子为空,右孩子不为空{//将删除节点的右孩子交给其父节点root = root->_rchild;//释放节点空间delete del;del = nullptr;}else//删除的节点左右孩子都不为空,要找到删除节点的左子树的最大节点或右子树的最小节点将其替换{//这里找要删除节点的右子树的最小节点(左子树的最大节点也可)Node* minright = del->_rchild; // 记录右子树的最小节点while (minright->_lchild)//查找右子树的最小节点{minright = minright->_lchild;}root->_key = minright->_key;//将找到的节点替换要删除的节点return _EraseR(root->_rchild, root->_key);//继续递归删除其右子树中用来替换的节点}return true;}}private:Node* _root = nullptr;//根节点
};
本期博客到这里就结束了,代码量较大,还请各位仔细分析呀
我们下期见~
相关文章:

【数据结构高阶】二叉搜索树
接下来我们来开始使用C来详细讲解数据结构的一些高阶的知识点 本期讲解的是二叉搜索树,对于初阶二叉树有所遗忘的同学可以看到这里: 【精选】【数据结构初阶】链式二叉树的解析及一些基本操作 讲解二叉搜索树主要是为了后面的map和set做铺垫ÿ…...
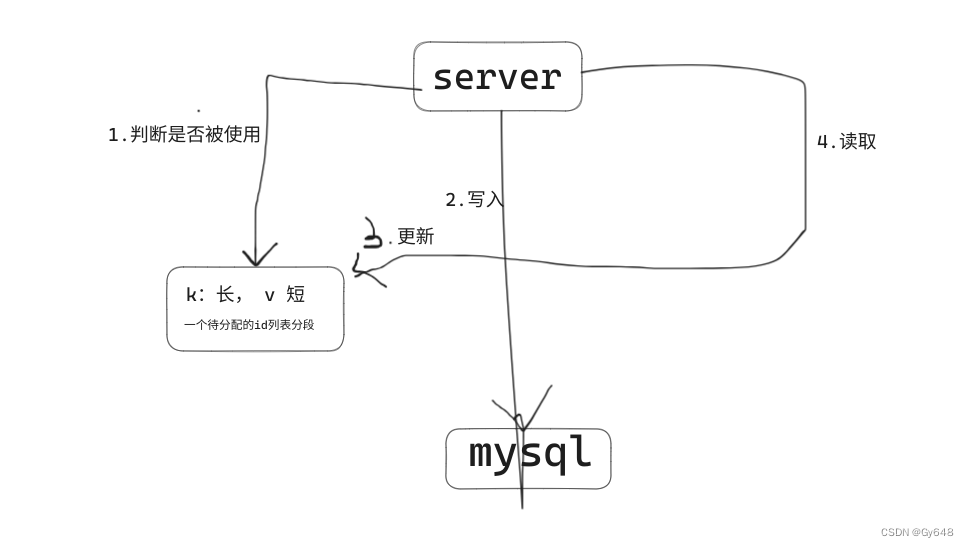
如何设计短域名系统
输入可能是 一个冗长的域名,过期时间和自定义的别名输出 自定义别名或者随机生成的短域名,在过期时间到来之前访问都可以被重定向到冗长的域名上约束条件 1.过期后就失效 2.短域名是唯一的 3.自定义短域名长度在7个字符(不包含域名长度&am…...
web缓存-----squid代理服务
squid相关知识 1 squid的概念 Squid服务器缓存频繁要求网页、媒体文件和其它加速回答时间并减少带宽堵塞的内容。 Squid代理服务器(Squid proxy server)一般和原始文件一起安装在单独服务器而不是网络服务器上。Squid通过追踪网络中的对象运用起作用。…...

nginx-location和proxy_pass的url拼接
在proxy_pass中端口号后面如果加入了"/",则location 匹配的内容全部去掉; Nginx中proxy_pass末尾带斜杠/和不带的区别 一、proxy_pass末尾有斜杠 location /api/ { proxy_pass http://127.0.0.1:8000/; } 请求地址:http://localhost/api/test 转发地…...

从零开始配置离线服务器
1.复制环境(包含torch包) 使用conda pack进行环境迁移(步骤很详细)_小舟%的博客-CSDN博客 注意:用pack的时候会默认把生成的tar.gz保存到当前目录,所以提前需要观测好在哪 注意:公用的环境必…...

Spring事务和事务的传播机制
目录 Spring中事务的实现 MySQL中的事务使用 Spring 编程式事务 TransactionTemplate 编程式事务 TransactionManager编程式事务 Spring声明式事务 Transactional 参数说明 事务因为程序异常捕获不会自动回滚的解决方案 Transactional 原理 Spring 事务隔离级别 Spring…...
软件开发提效工具——低代码(Low-Code)
目录 一、什么是低代码(Low-Code)? 二、构建轻量化平台 1、软件开发快效率高 2、满足企业的多样化需求 3、轻松与异构系统集成 4、软件维护成本低 5、为企业实现降本增效 三、小结 一、什么是低代码(Low-Code)…...
菜单栏管理软件 Bartender 3 mac中文版功能介绍
Bartender 3 mac是一款菜单栏管理软件,该软件可以将指定的程序图标隐藏起来,需要时呼出即可。 Bartender 3 mac功能介绍 Bartender 3完全支持macOS Sierra和High Sierra。 更新了macOS High Sierra的用户界面 酒吧现在显示在菜单栏中,使其…...

ef core code first pgsql
在使用efcode来操作pgsql的时候,总有些基础配置流程项目建立完之后后面就很少用,总是忘掉,写个文档记忆一下吧。基于net 6.0。 1.创建一个mvc项目和一个EF类库 2.在类库里面安装依赖dll Microsoft.EntityFrameworkCore.Design 需要添加的…...

容器化nacos部署并实现服务发现(gradle)
1.如何容器化部署mysql 2. 如何容器化部署nacos 为不暴露我的服务器地址,本文全部使用localhost来代替服务器地址,所有的localhost都应该调整为你自己的服务器地址。 为不暴露我的服务器地址,本文全部使用localhost来代替服务器地址&#x…...

金融行业如何数字化转型?_光点科技
金融行业的数字化转型涉及技术创新的引入、客户体验的改善、内部流程的优化、安全和合规性的加强以及员工技能和企业文化的转变。 技术创新 包括云计算、人工智能、大数据分析和区块链技术的采用。云计算增强数据处理的灵活性,AI和机器学习在风险评估和欺诈检测方面…...
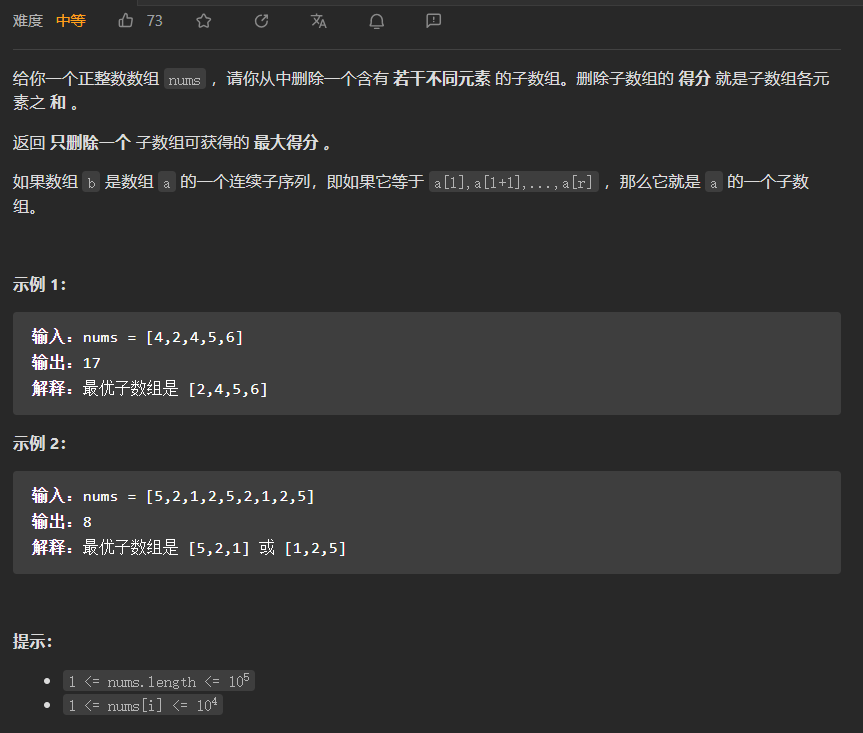
【LeetCode刷题-滑动窗口】--1695.删除子数组的最大得分
1695.删除子数组的最大得分 注意:子数组为不同元素 方法:滑动窗口 使用变长滑动窗口寻找数组nums中的以每个下标作为结束下标的元素各不相同的最长子数组。用[start,end]表示滑动窗口,初始时startend0,将滑动窗口的右端点end向右…...
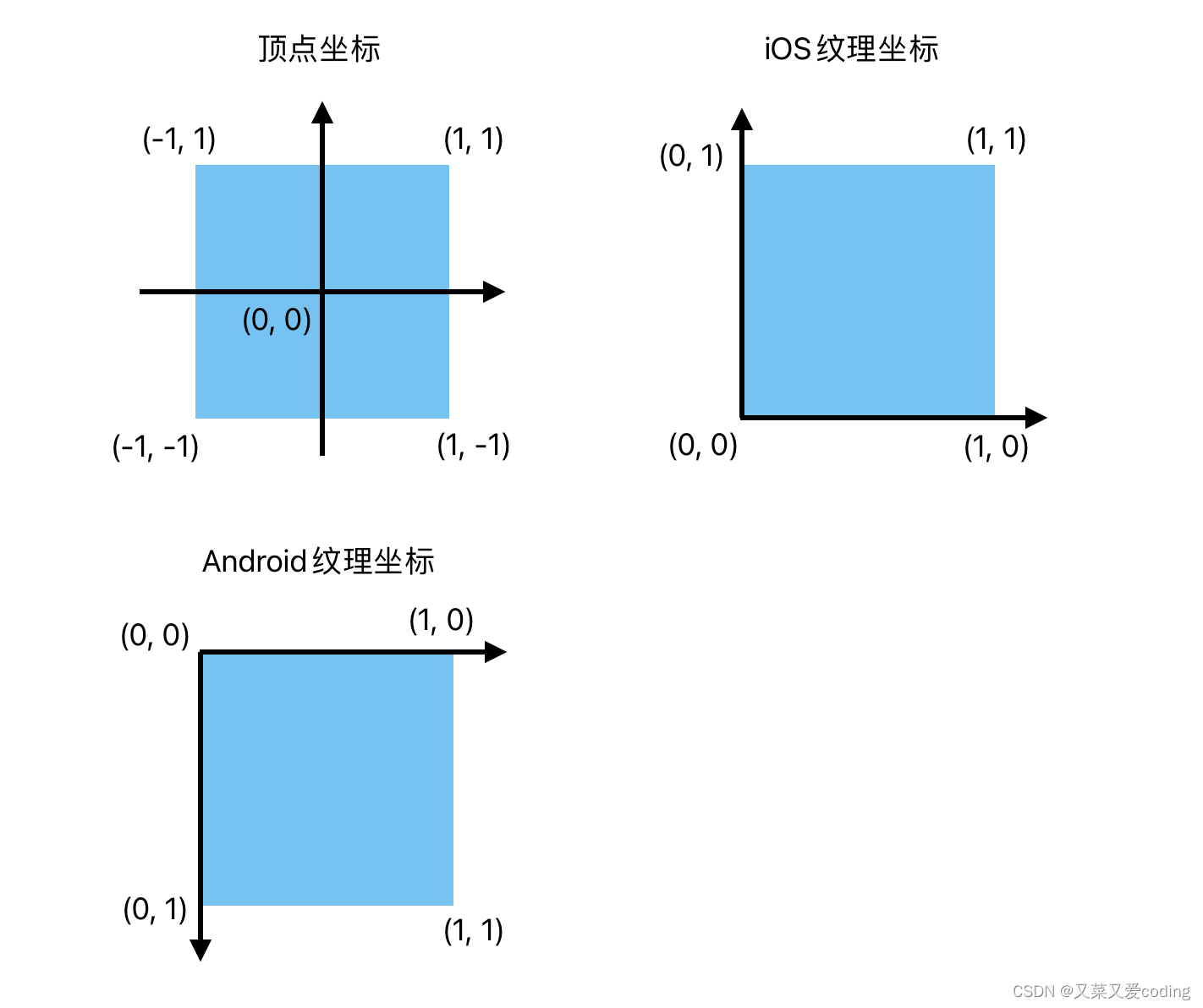
iOS OpenGL ES3.0入门实践
一、效果图 入门实践,做的东西比较简单,效果如下: 二、关于顶点坐标和纹理坐标 绘制图片需要设置顶点坐标和纹理坐标并加载像素数据,之所以要指定两组坐标是因为纹理和顶点使用不同的坐标系,就是告诉OpenGL…...
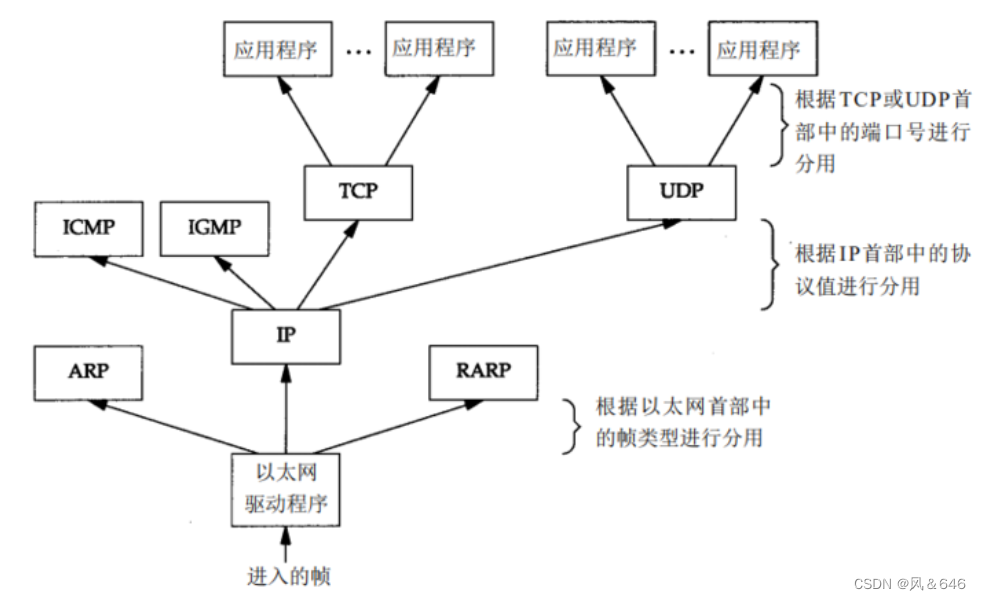
网络基础(一)
文章目录: 计算机网络认识计算机网络背景网络发展认识 “协议” 网络协议初识协议分层OSI七层模型TC/IP 五层(或四层)模型 网络传输基本流程网络传输流程图同局域网的两台主机进行通信跨网络的两台主机进行通信数据包的封装和分用 网络中的地…...
SQLServer添加Oracle链接服务器
又一次在项目中用到了在SQLServer添加Oracle链接服务器,发现之前文章写的也不太好使,那就再总结一次吧。 1、安装OracleClient 安装64位,多数SQLServer是64位,所以OracleClient也安装64位的; 再一个一般安装的Oracl…...
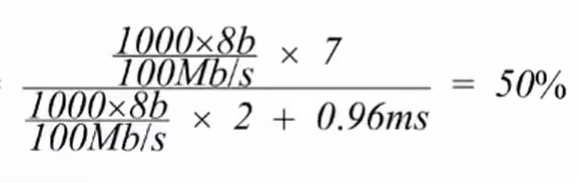
2017年计网408
第33题 假设 OSI 参考模型的应用层欲发送 400B 的数据 (无拆分), 除物理层和应用层之外, 其他各层在封装 PDU 时均引入 20 B 的额外开销, 则应用层数据传输效率约为( )A. 80%B. 83%C. 87%D. 91% 本题考察有关数据包逐层封装的相关概念。我们来一起分析一下。 这是要求大家必须…...
)
UE5中APlayerController属性与方法列表(翻译中......)
一、属性列表 类型 名称 描述 TObjectPtr< APa... AcknowledgedPawn 用于网络游戏,使客户端可以承认它拥有一个特定的卒。 TArray< FActive... ActiveForceFeedbackEffects TSharedPtr< str... ActiveHapticEffect_Gun TSharedPtr< str..…...
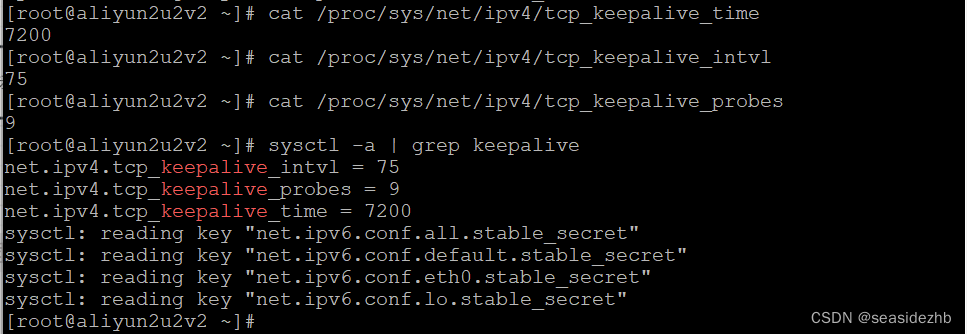
TCP连接保活机制
在TCP连接中有一个保活机制,叫做Keep-Alive,用语言描述就是如下: 在保活时间内,如果没有任何连接相关的活动,TCP 保活机制会开始作用,每隔一个时间间隔(保活时间间隔),发…...

centos安装mysql8.0.20、tar包安装方式
基础环境centos7.5,mysql版本8.0.20,通过tar包安装,安装路径/usr/local。 mysql官网:https://dev.mysql.com/downloads/mysql/ wget https://dev.mysql.com/get/Downloads/MySQL-8.0/mysql-8.0.20-linux-glibc2.12-x86_64.tar.x…...

k8s yaml文件含义
文章目录 1、YAML的文件格式和注意事项2、YAML各个字段含义 1、YAML的文件格式和注意事项 不支持制表符tab键缩进,需要使用空格缩进,使用缩进表示层级关系通常开头缩进2个空格,缩进的空格数不重要,只要相同层级的元素左对齐即可字…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
