代码随想录算法训练营第五十五天 | LeetCode 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结
代码随想录算法训练营第五十五天 | LeetCode 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结
文章链接:两个字符串的删除操作、编辑距离、编辑距离总结
视频链接:两个字符串的删除操作、编辑距离
1. LeetCode 583. 两个字符串的删除操作
1.1 思路
- 题目给我们两个字符串问两个字符串最少可以删除多少个元素使这两个字符串相同。本题相对于115. 不同的子序列难在于两个都可以删
- dp 数组及其下标的含义:比较两个字符串里的每个元素是否相同的情况就定义二维数组,dp[i][j]:以 i-1 为结尾的 word1 和以 j-1 为结尾的 word2,为了让它们相同的最少操作次数为 dp[i][j]。定义 i-1 和 j-1 是为了方便初始化
- 递推公式:if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1] 因为这两个元素已经相同了,考虑与不考虑都是一样的,因此直接继承dp[i-1][j-1],因为两个元素都相同了就可以不操作它们了。else 就是word1[i-1]!=word2[j-1] 的情况就需要删除元素了,如果删除word1[i-1],dp[i][j]=dp[i-1][j]+1 这里就是模拟出了删除 word1[i-1];如果删除word2[j-1],dp[i][j]=dp[i][j-1]+1 这里就是模拟出了删除 word2[j-1];如果都删了就是 dp[i][j]=dp[i-1][j-1]+2。因此如果两个元素不相同就是 dp[i][j]=Math.min(三个取最小值)
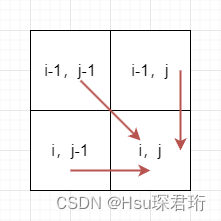
- dp 数组的初始化:根据递推公式得到推导方向,因此第一行和列都需要初始化,dp[0][j] 表示以-1 为结尾即空字符串 word1,要想和 word2 相同的最小操作次数就应该是 j,因为 word2 就需要删掉 j 个元素;dp[i][0] 表示以-1 为结尾即空字符串 word2,要想和 word1 相同的最小操作次数就应该是 1,因为 word1 就需要删掉 i 个元素。其余下标因为会被覆盖,因此默认即可
- 遍历顺序:从推导方向可以看出就是从左到右从上到下, for(int i=1;i<=word1.length();i++)for(int j=1;word2<=t.length();j++),为什么从 1 开始?为什么要等于号?以前解释过了。最终结果保存在 dp[word1.length()][word2.length()]
- 打印 dp 数组:用于 debug
- 其实本题也可以通过求1143. 最长公共子序列一样,求出最长公共子序列,然后两个原字符串总和相加减去 2 倍的最长公共子序列的长度就是要求的最小操作次数
1.2 代码
// dp数组中存储需要删除的字符个数
class Solution {public int minDistance(String word1, String word2) {int[][] dp = new int[word1.length() + 1][word2.length() + 1];for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;for (int i = 1; i < word1.length() + 1; i++) {for (int j = 1; j < word2.length() + 1; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));}}}return dp[word1.length()][word2.length()];}
}
//DP - longest common subsequence (用最長公共子序列反推)
class Solution {public int minDistance(String word1, String word2) {char[] char1 = word1.toCharArray();char[] char2 = word2.toCharArray();int len1 = char1.length;int len2 = char2.length;int dp[][] = new int [len1 + 1][len2 + 1];for(int i = 1; i <= len1; i++){for(int j = 1; j <= len2; j++){if(char1[i - 1] == char2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}return len1 + len2 - (2 * dp[len1][len2]);//和leetcode 1143只差在這一行。}
}
2. LeetCode 72. 编辑距离
2.1 思路
- 本题是给我们两个字符串,如何让 word1 和 word2 相等,可以通过添加、删除、替换元素,对 word1 和 word2 操作都可以,增加 word1 的元素也就是相当于删除 word2 的元素,因此操作方式很多样
- dp 数组及其下标的含义:比较两个字符串的相同情况我们要定义一个二维数组,dp[i][j]:以 i-1 为结尾的 word1 和以 j-1 为结尾的 word2 最少操作次数为 dp[i][j] 能使两个字符串相等。为什么以 i-1 和 j-1 结尾是为了方便初始化
- 递推公式:要求相同就要比较每个元素,讨论它们相同与不相同的情况 if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1] 因为两个元素都相同了,就可以不改变操作次数,不需要任何操作。else 就是两个元素不相同,有增加、删除、替换等操作,如果删掉 word1 的第 i-1 个元素,那就是 dp[i][j]=dp[i-1][j]+1,也就是以 i-2 为结尾和以 j-1 为结尾的相同的最小操作数的基础上+1,如果删掉 word2 的第 j-1 个元素,dp[i][j]=dp[i][j-1]+1,如果两个元素不相同选择替换元素,无论是替换 word1 的还是 word2 的,把其中一个的替换成另一个的就可以了,因此是 dp[i][j]=dp[i-1][j-1]+1,这里含义是把 word1 的第 i-1 个元素换成了 word2 的第 j-1 个元素或者 word2 的第 j-1 个元素换成了 word1 的第 i-1 个元素。因此 dp[i][j]=Math.min(三者取最小值)。为什么这里没有添加元素的操作呢?因为对 word1 添加其实就相当于对 word2 删除,反之也是同理,因此我们用删除代替了添加,效果是一样的
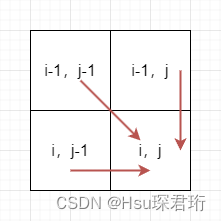
- dp 数组的初始化:根据递推公式得到推导方向,因此我们要初始化第一行和列都初始化了,dp[i][0],也就是以 i-1 为结尾的字符串 word1 和以-1 为结尾的空字符串 word2,word1 要最少操作 i 次才能与 word2 相等,因此 for(int i=0;i<=word1.length();i++)dp[i][0]=i;dp[0][j],以-1 为结尾的空字符串 word1 和以 j-1 为结尾的字符串 word2,word2 最少操作 j 次才能与 word1 相等,因此 for(int j=0;j<=word2.length();j++)dp[0][j]=j。为什么取等于号,因为 dp是以 i-1 为结尾和 j-1 为结尾的,一定要取等了,才能表示最后一个元素为结尾。其余下标无所谓,会被覆盖,默认为 0 即可。
- 遍历顺序:根据递推公式和推导方向,就一定是从左到右和从上到下,for(int i=1;i<=word1.length();i++)for(int j=1;word2<=t.length();j++),为什么从 1 开始?为什么取等于号?上面解释过了。最终结果保存在 dp[word1.length()][word2.length()]
- 打印 dp 数组:用于 debug
2.2 代码
public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];// 初始化for (int i = 1; i <= m; i++) {dp[i][0] = i;}for (int j = 1; j <= n; j++) {dp[0][j] = j;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 因为dp数组有效位从1开始// 所以当前遍历到的字符串的位置为i-1 | j-1if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;}}}return dp[m][n];
}
3. 编辑距离总结
本题是通过三道题铺垫而来的
3.1 392. 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
这道题目 其实是可以用双指针或者贪心的的,但是我在开篇的时候就说了这是编辑距离的入门题目,因为从题意中我们也可以发现,只需要计算删除的情况,不用考虑增加和替换的情况。
- if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
状态转移方程:
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];
3.2 115. 不同的子序列
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
本题虽然也只有删除操作,不用考虑替换增加之类的,但相对于392. 判断子序列就有难度了,这道题目双指针法可就做不了。
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
这里可能有同学不明白了,为什么还要考虑 不用s[i - 1]来匹配,都相同了指定要匹配啊。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配,即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
状态转移方程:
if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {dp[i][j] = dp[i - 1][j];
}
3.3 583. 两个字符串的删除操作
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最少步数,每步可以删除任意一个字符串中的一个字符。
本题和115. 不同的子序列相比,其实就是两个字符串可以都可以删除了,情况虽说复杂一些,但整体思路是不变的。
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
状态转移方程:
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
} else {dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}
3.4 72. 编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
编辑距离终于来了,有了前面三道题目的铺垫,应该有思路了,本题是两个字符串可以增删改,比392. 判断子序列、115. 不同的子序列、583. 两个字符串的删除操作要复杂很多
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
- if (word1[i - 1] == word2[j - 1])
- 不操作
- if (word1[i - 1] != word2[j - 1])
- 增
- 删
- 换
也就是如上四种情况。
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
此时可能有同学有点不明白,为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1] 就是 dp[i][j]了。
在下面的讲解中,如果哪里看不懂,就回想一下dp[i][j]的定义,就明白了。
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
操作一:word1增加一个元素,使其word1[i - 1]与word2[j - 1]相同,那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离 加上一个增加元素的操作。
即 dp[i][j] = dp[i - 1][j] + 1;
操作二:word2添加一个元素,使其word1[i - 1]与word2[j - 1]相同,那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个增加元素的操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了,怎么都是添加元素,删除元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word2添加一个元素d,也就是相当于word1删除一个元素d,操作数是一样!
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增加元素,那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。
即 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
递归公式代码如下:
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
相关文章:

代码随想录算法训练营第五十五天 | LeetCode 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结
代码随想录算法训练营第五十五天 | LeetCode 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结 文章链接:两个字符串的删除操作、编辑距离、编辑距离总结 视频链接:两个字符串的删除操作、编辑距离 1. LeetCode 583. 两个字符串的删除操作 1.1 思…...
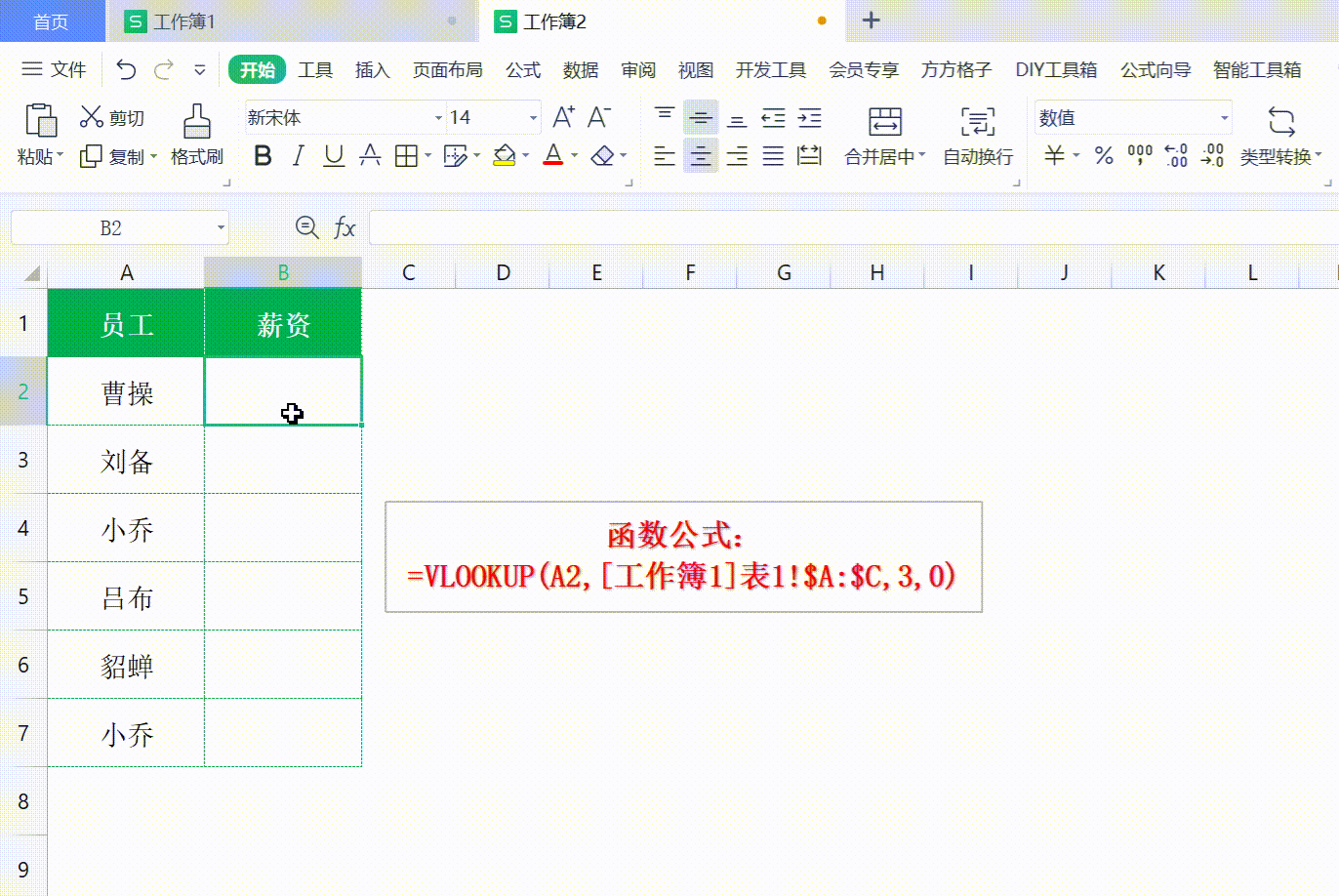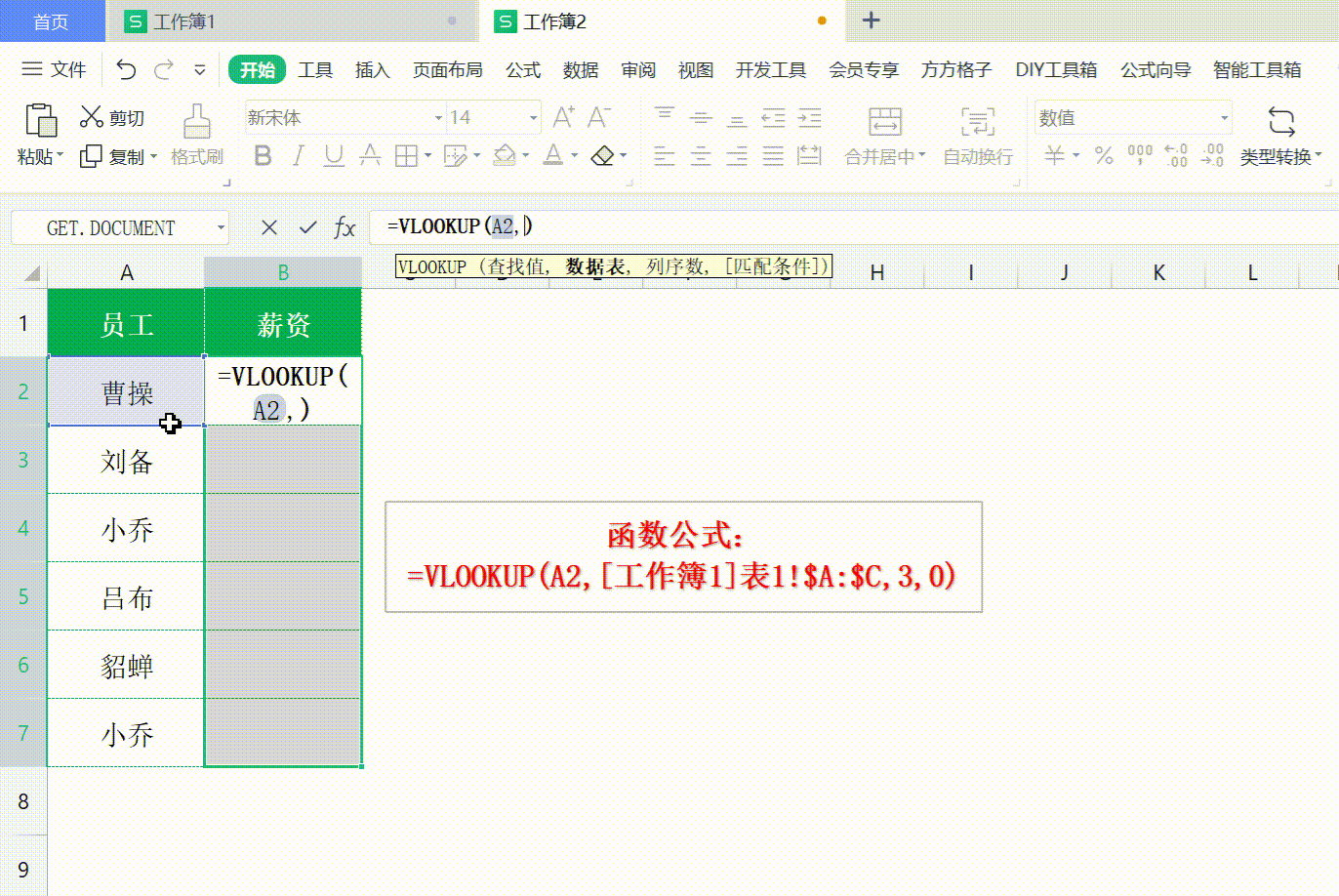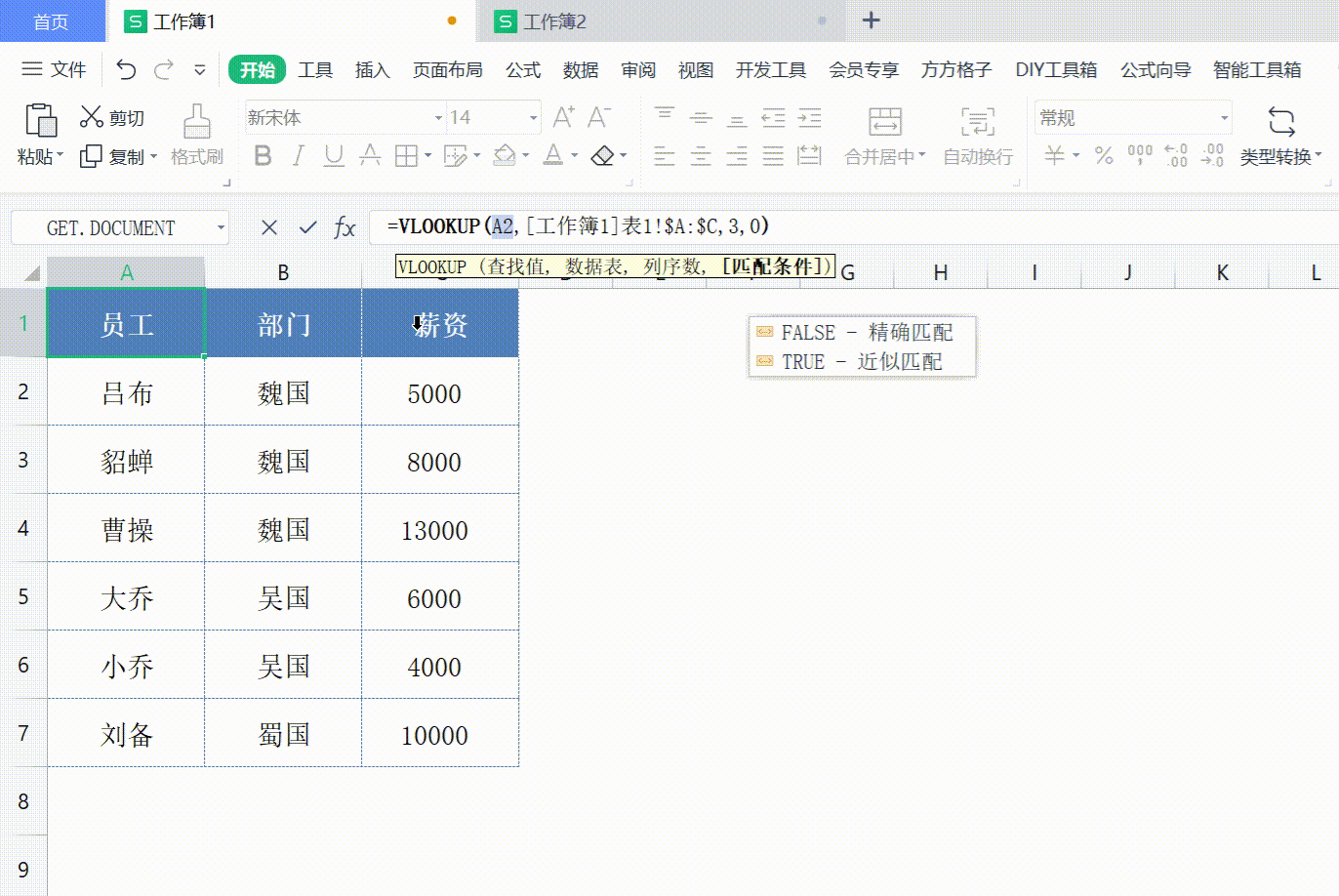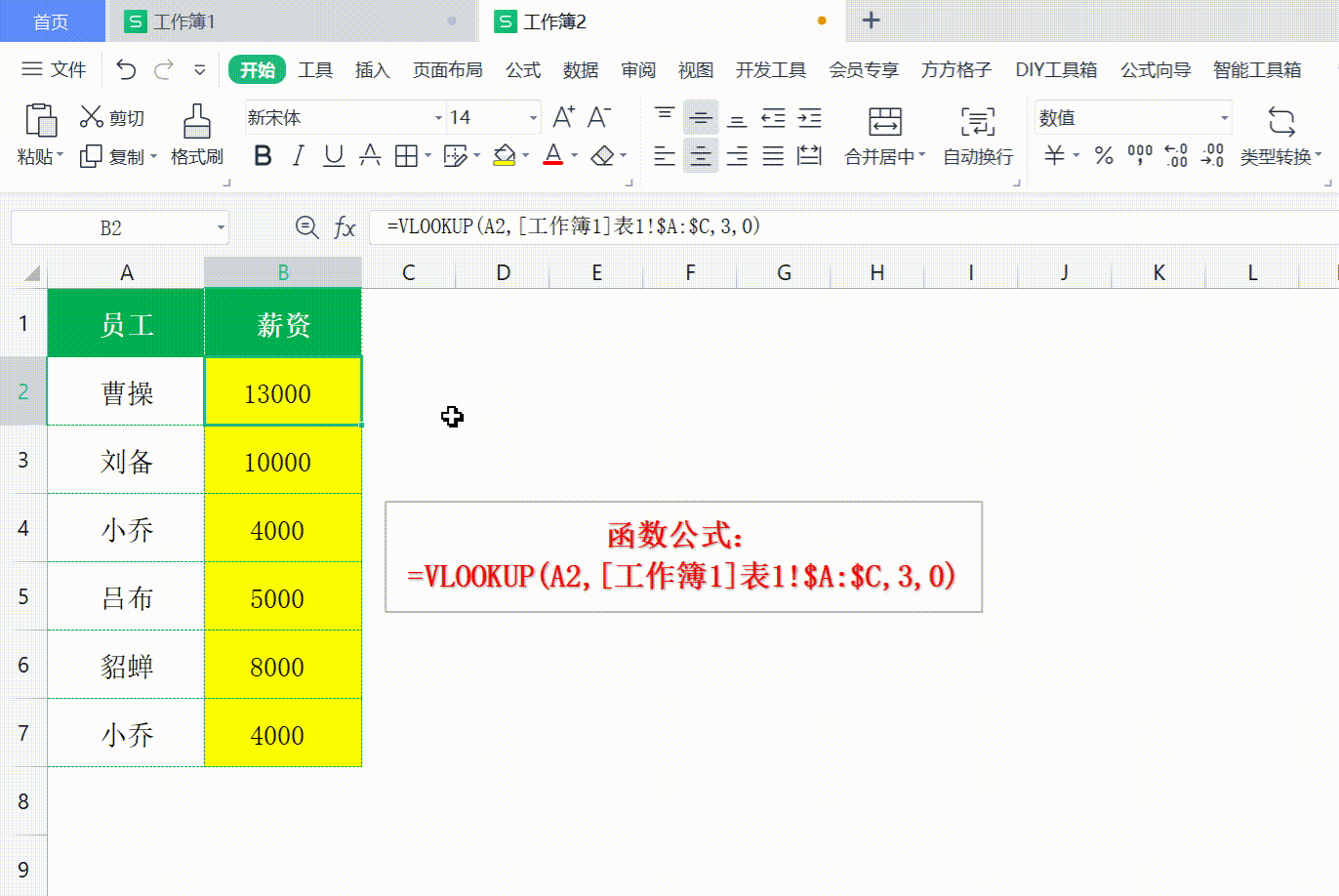
Excel vlookup 如何使用
Excel vlookup 如何使用 打开WX, 搜索 “程序员奇点” Excel vlookup可以说是利器,非常好用的工具,用来查询 Excel 或者进行数据匹配,十分方便。 VLookuP 如何使用,不常用的同学经常容易忘记,这次做个记录ÿ…...

Latex常用特殊字符汇总
本文汇总了博主在使用Latex写文档过程中遇到的所有常用疑难字符、表达式等等及对应的Latex形式 持续更新... 目录 常用字符波浪号1. 文本模式:~2. 数学模式: ∼ \sim ∼3. 字母上方的波浪号: a ˜ \~a a˜ 字母上方角标 (数学模式强调符)箭头…...
Day1跟李沐学AI-深度学习课程00-04【预告、课程安排、深度学习介绍、安装、数据操作+数据预处理】
00 预告 《动手学深度学习》https://github.com/d2l-ai/d2l-zh 01 课程安排 02 深度学习介绍 03 安装 本地安装 使用conda/miniconda环境 conda env remove d2l-zh conda create -n -y d2l-zh python3.8 pip conda activate d2l-zh 安装需要的包 pip install -y jupyter …...
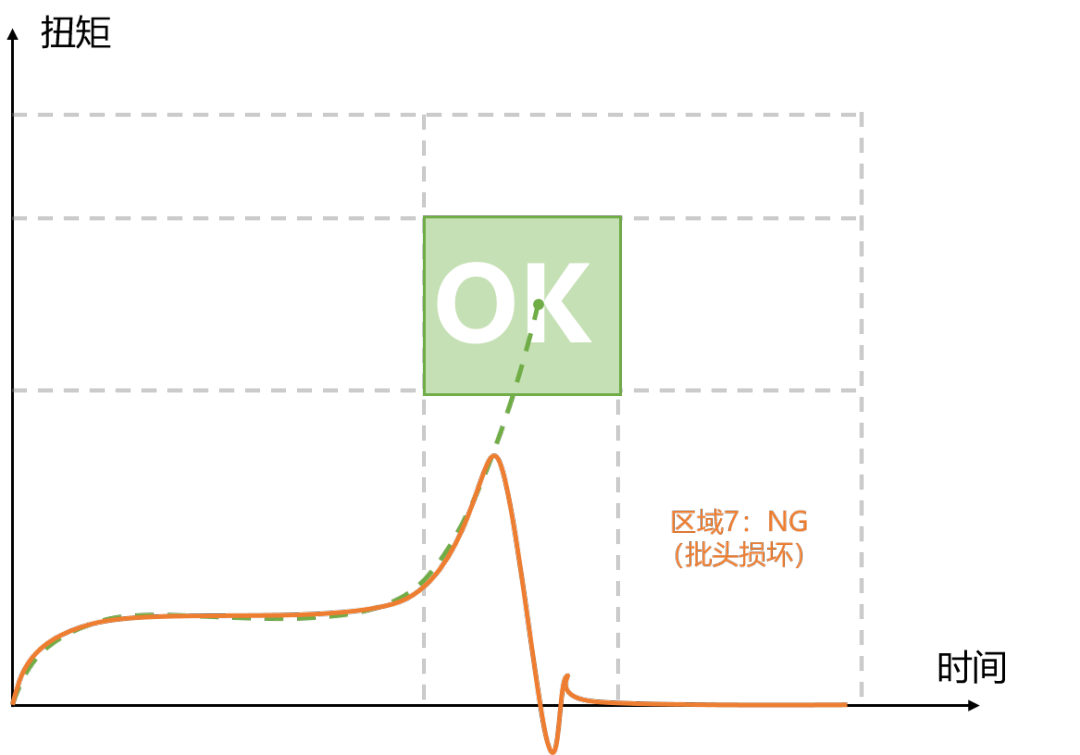
借助拧紧曲线高效管理螺栓装配防错——SunTorque智能扭矩系统
拧紧曲线作为拧紧质量的“晴雨表”,在拧紧过程中,能够实时探知到拧紧状态是否存在异常,并根据曲线特质推测出拧紧过程中遇到了什么样的问题,今天SunTorque智能扭矩系统带您了解拧紧曲线在螺栓装配防错管理中如何发挥作用。 合格的…...

李开复再度回应争议;10 月中国游戏厂商及应用出海收入 30 强出炉丨 RTE 开发者日报 Vol.86
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE (Real Time Engagement) 领域内「有话题的 新闻 」、「有态度的 观点 」、「有意思的 数据 」、「有…...

mysql undolog
undolog 日志介绍...

milvus数据库-管理数据库
一个 Milvus 集群最多支持 64 个数据库。 1.创建数据库 先连接数据库服务器,再创建 from pymilvus import connections, dbconn connections.connect(host"127.0.0.1", port19530)database db.create_database("book")2.连接数据库 可以改变…...

一键整合,万用万灵,Python3.10项目嵌入式一键整合包的制作(Embed)
我们知道Python是一门解释型语言,项目运行时需要依赖Python解释器,并且有时候需要安装项目中对应的三方依赖库。对于专业的Python开发者来说,可以直接通过pip命令进行安装即可。但是如果是分发给其他的Windows用户,特别是不熟悉Py…...
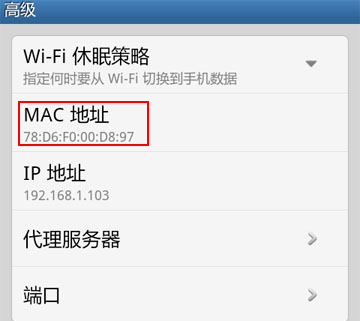
MAC地址注册的网络安全影响和措施分析
MAC地址注册对网络安全具有重要影响,同时也需要采取相应的措施来应对潜在的安全风险。以下是有关MAC地址注册的网络安全影响和应对措施的分析: 影响: 1. 身份验证:MAC地址注册可用于设备的身份验证,但MAC地址本身并不…...
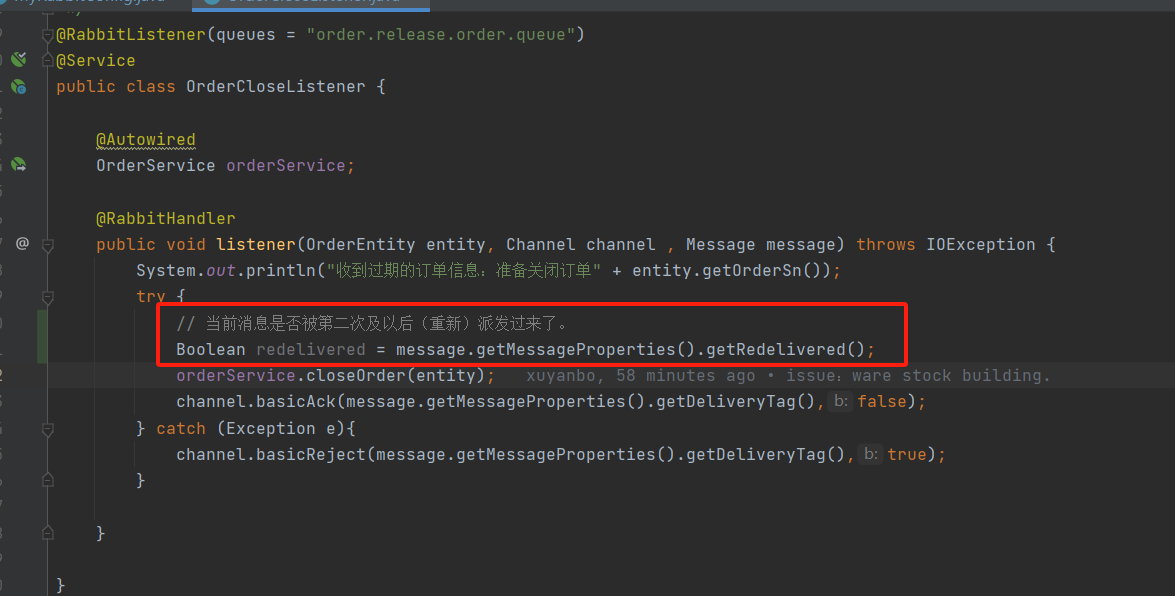
某个订单项目记录,涉及MQ消息处理、分布式问题、幂等性等问题解决设计
文章目录 消息队列(Message Queue)什么场景下,使用消息队列?消息队列 概述 RabbitMQ 消息队列RabbitMQ 概念名词 概念RabbitMQ 流程 RabbitMQ 安装RabbitMQ 页面介绍Exchange 交换机类型Spring Boot 整合RabbitMQAmqpAdmin 与 Rab…...
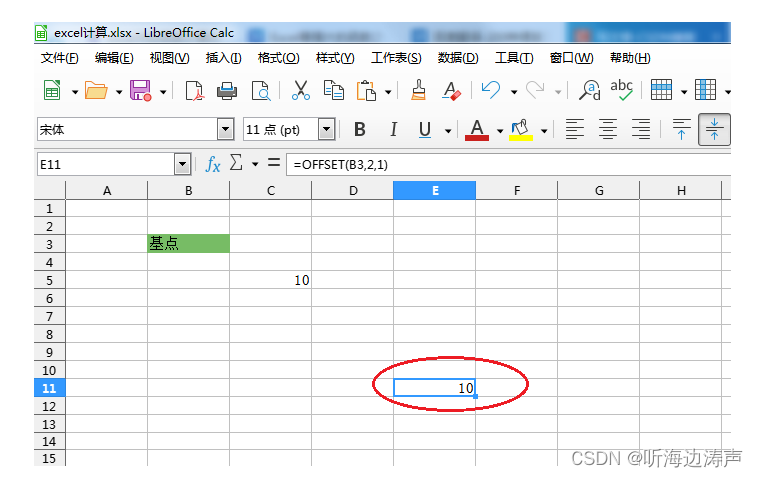
excel中的OFFSET函数
介绍 OFFSET函数是确定从基点出发移动后的引用区域。它有5个参数: 第1个参数是引用的参考基点区域第2个参数是移动的行数,正数代表向下移动的行数,负数代表向上移动的行数第3个参数是移动的列数,正数代表向右移动的列数…...
)
力扣:168. Excel表列名称(Python3)
题目: 给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称。 例如: A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ... 来源:力扣(LeetCode) 链接:力扣&…...
短视频账号矩阵系统源码/技术源码分享/技术搭建架构
短视频账号矩阵系统----技术源码分享/技术搭建架构 抖音seo又叫抖音搜索引擎,只要能做到布词,和过去的百度seo优化一样,布词,布关键词,当搜索栏搜索时可以搜索到该短视频。优化视频关键词,做好关键词的优化…...

Nginx负载均衡时,验证码老是错误
问题 正式环境里,登录之后没有跳转到之前的页面,在测试服务器上测试了一下这个BUG,不存在这个问题 问题原因 我们的服务器做了负载均衡,问题出现之后,就问了运维,负载均衡的规则是什么,默认情况…...

Unity3D ugui获取ui控件屏幕坐标
local worldPos uiGo.Transform.position local uiCamera GetUICamera() local screenPos uiCamera:WorldToScreenPoint(worldPos)...

数字化转型的“支点”是什么?
当前,数字化转型在推动各行各业降本增效的过程中扮演着越来越重要的角色,数字化转型不仅可以提高企业的生产效率和降低企业生产经营成本,也成为了推动经济发展的新引擎。对于企业而言,想要成功推动企业数字化转型,不…...
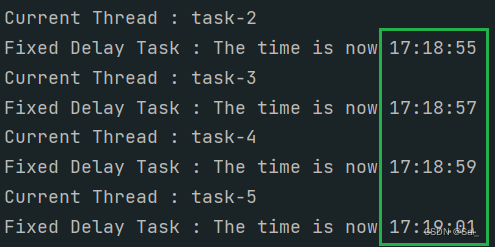
Spring Task单机定时任务(使用及阻塞问题解决)
一、介绍 SpringTask是Spring自主研发的定时任务工具,并且存在于Spring体系中,不需要添加任何依赖 Spring Boot 默认在无任何第三方依赖的情况下使用 spring-context 模块下提供的定时任务工具 Spring Task。 我们只需要使用 EnableScheduling 注解就可…...

石原子科技亮相2023成都市信息领域新产品发布会
2023年11月13日至15日,由成都市互联网信息办公室、四川天府新区管委会、成都市经信局市新经济委、成都市农业农村局指导的以“信息创造价值 创新引领未来”为主题的成都市信息领域新产品发布会在科创生态岛1号馆举行。围绕人工智能、区块链、数字化绿色化、数字乡村…...

2023数维杯国际赛数学建模竞赛选题建议及D题思路讲解
大家好呀,2023年第九届数维杯国际大学生数学建模挑战赛今天早上开赛啦,在这里先带来初步的选题建议及思路。 目前团队正在写B题和D题完整论文,后续还会持续更新哈,大家三连关注一下防止迷路。 注意,本文只是比较简略…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
