python语言实现背包问题动态规划
背包问题是一个经典的动态规划问题,实现方式如下:
假设有一个背包,容量为 W,有 n 个物品,每个物品有两个属性:体积 v 和价值 w。要求在不超过背包容量的情况下,选取一些物品放入背包,使得背包中物品的价值最大。
使用一个二维数组 dp 来记录每个状态的最优解,其中 dp[i][j] 表示考虑前 i 个物品,且背包容量为 j 时的最大价值。
状态转移方程如下:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])
其中,第一部分 dp[i-1][j] 表示不选第 i 个物品,背包容量不变;第二部分 dp[i-1][j-v[i]] + w[i] 表示选第 i 个物品,背包容量减少 v[i],价值增加 w[i]。
最终的最大价值为 dp[n][W]。
下面是 Python 代码实现:
def knapsack(W, n, v, w):# 初始化 dp 数组dp = [[0] * (W+1) for _ in range(n+1)]for i in range(1, n+1):for j in range(1, W+1):if j < v[i]:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])return dp[n][W]
其中,W 表示背包容量,n 表示物品数量,v 和 w 分别表示每个物品的体积和价值。
调用 knapsack 函数,即可求出最大价值。
相关文章:

python语言实现背包问题动态规划
背包问题是一个经典的动态规划问题,实现方式如下: 假设有一个背包,容量为 W,有 n 个物品,每个物品有两个属性:体积 v 和价值 w。要求在不超过背包容量的情况下,选取一些物品放入背包࿰…...

将Python程序(.py)转换为Windows可执行文件(.exe)
python开发者向普通windows用户分享程序,要给程序加图形化的界面(传送门:这可能是最好玩的python GUI入门实例! http://www.jianshu.com/p/8abcf73adba3),并要将软件打包为可执行文件(.exe结尾),那如何将.py转为.exe ? 将.py转为.exe 第一步:安装pyinstaller(临时调用了国内豆…...

Oracle 查找非系统用户结合了10,11,12,19
oracle 12开始有了INHERITEDYES;字段来区分系统用户 select username from dba_users where INHERITEDYES; 对于12以下的版本,按created日期字段筛选会发现创建时间间隔比较大,好区分。 本人当前有个需求需要找出所有数据库的非系统用户,来…...

c++虚函数纯虚函数详解加代码解释
c虚函数纯虚函数详解加代码解释 一.概念:二.虚函数示例及解析:三.纯虚函数示例及解析:四.验证和实际使用及解析:1.子类没有对父类的函数重载,mian()函数调用,是直接返回父类的值2.子类对父类的函数重载&…...

kotlin retrofit
参考博客 【Android】【Kotlin】使用【Retrofit】基本使用 如何在kotlin中正确使用retrofit 将kotlin协程用于网络请求—完整实例,看这一篇就够了 Kotlin协程Retorfit网络请求框架封装...

Web 开发中 route 和 router 有什么区别?
什么是路由? 在 Web 开发中,会经常和路由打交道,可能有的同学并没有仔细思考过到底什么是路由。路由是根据用户请求的 URL 来确定返回给用户的内容或页面的技术,即将 HTTP 请求映射到相应的处理代码,使得用户能够通过…...

VBA技术资料MF83:将Word文档批量另存为PDF文件
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
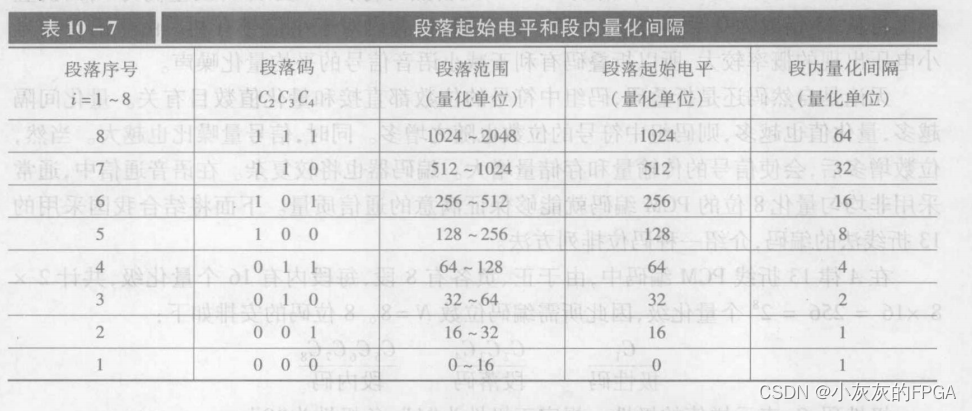
通信原理板块——脉冲编码调制(PCM)
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等 1、脉冲编码调制PCM原理 将模拟信号…...
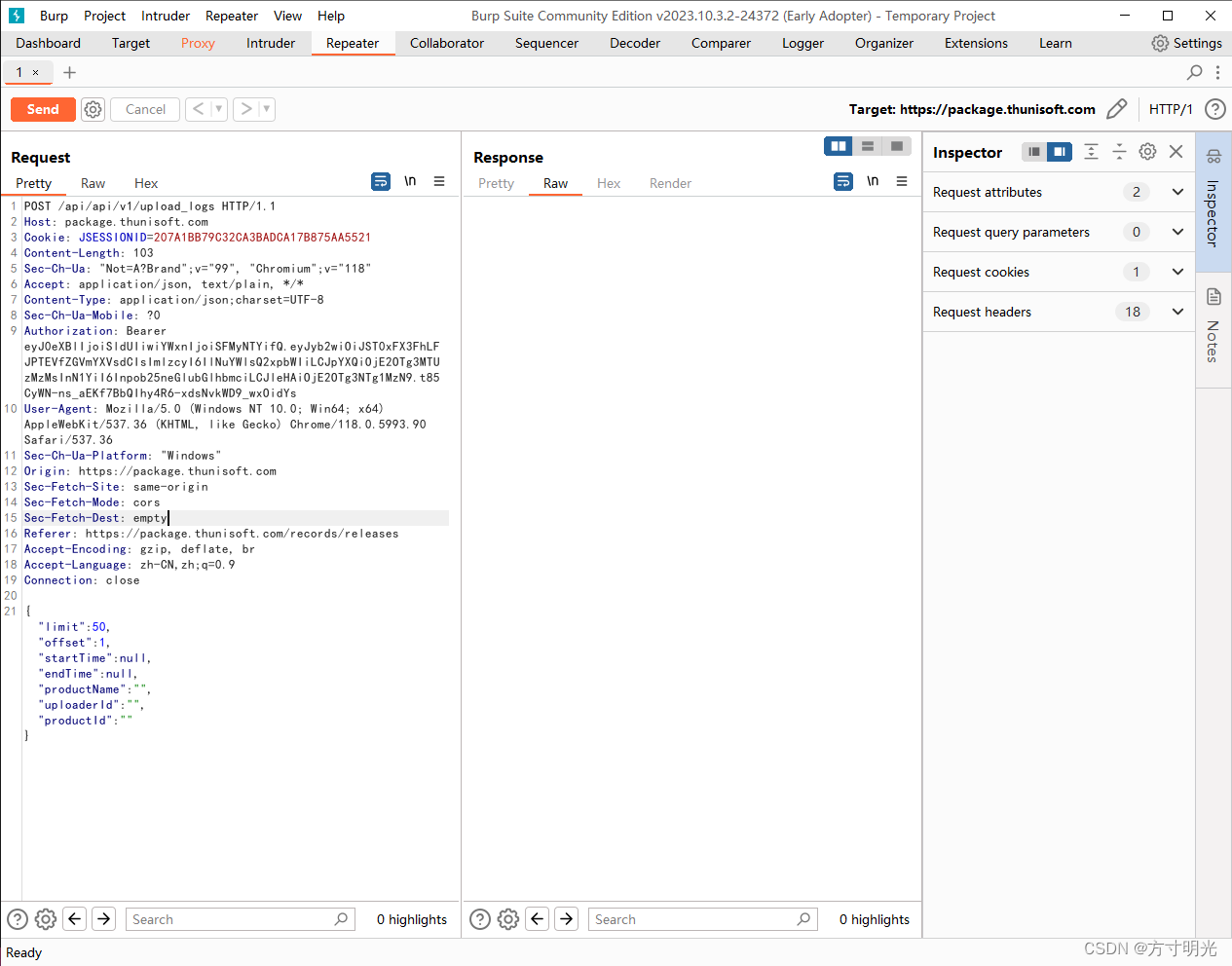
绕过类安全问题分析方法
什么是绕过 逻辑漏洞是指程序设计中逻辑不严密,使攻击者能篡改、绕过或中断程序,令其偏离开发人员预期的执行。 常见表现形式 1、接口(功能类)绕过:即接口或功能中通过某参数,绕过程序校验 2、流程类绕…...
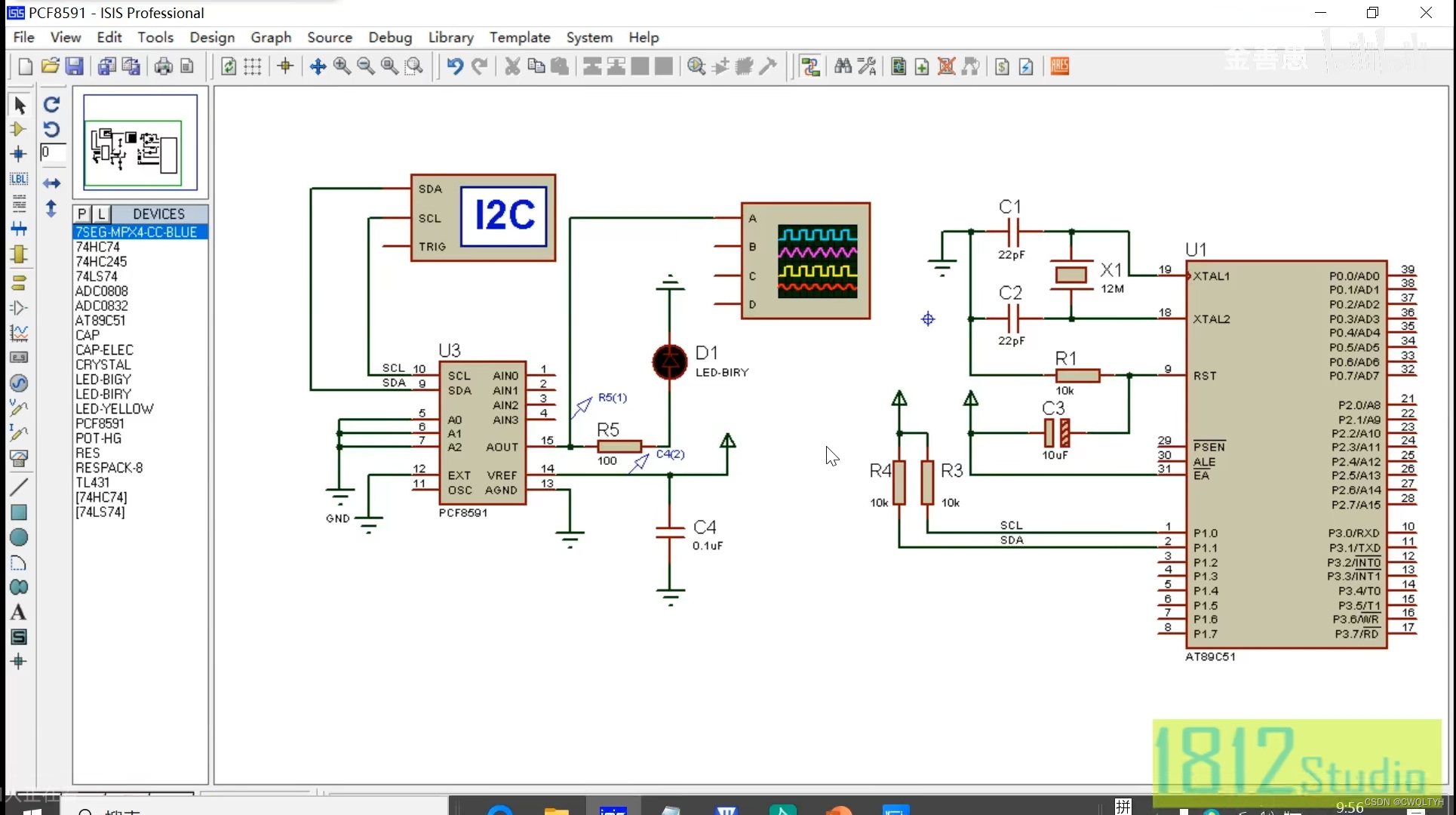
基于STC12C5A60S2系列1T 8051单片的IIC总线器件数模芯片PCF8591实现数模转换应用
基于STC12C5A60S2系列1T 8051单片的IIC总线器件数模芯片PCF8591实现数模转换应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍IIC总线器件数模芯片PCF8591介绍通过按…...

2023年中国骨质疏松治疗仪发展趋势分析:小型且智能将成为产品优化方向[图]
骨质疏松治疗仪利用磁场镇静止痛、消肿消炎的治疗作用迅速缓解患者腰背疼痛等骨质疏松临床症状。同时利用磁场的磁-电效应产生的感生电势和感生电流,改善骨的代谢和骨重建,通过抑制破骨细胞、促进成骨细胞的活性来阻止骨量丢失、提高骨密度。 骨质疏松治…...
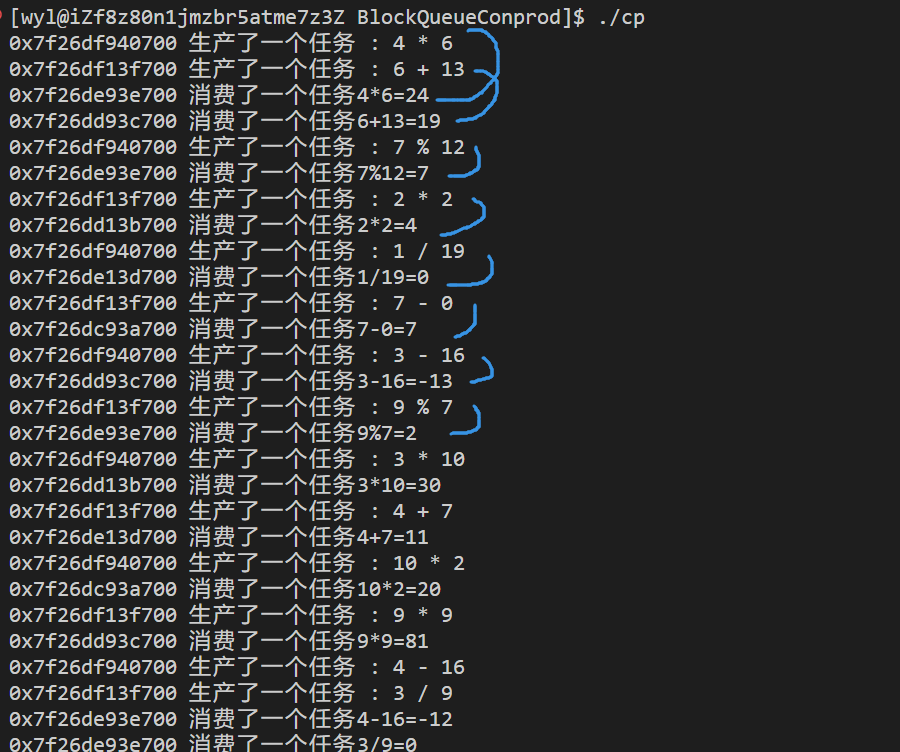
并发编程之生产者消费者模型
什么是生产者消费者模型 生产者消费者模型是多线程中一个比较典型的模型。 打个比方:你是一个客户,你去超市里买火腿肠。 这段话中的 "你"就是消费者, 那么给超市提供火腿肠的供货商就是生产者。超市呢?超市是不是被…...

Java要将字符串转换为Map
Java要将字符串转换为Map,可以使用以下方法: import com.google.gson.Gson; import com.google.gson.reflect.TypeToken; import java.lang.reflect...

2760. 最长奇偶子数组 --力扣 --JAVA
题目 给你一个下标从 0 开始的整数数组 nums 和一个整数 threshold 。 请你从 nums 的子数组中找出以下标 l 开头、下标 r 结尾 (0 < l < r < nums.length) 且满足以下条件的 最长子数组 : nums[l] % 2 0 对于范围 [l, r - 1] 内的所有下标 i ,…...
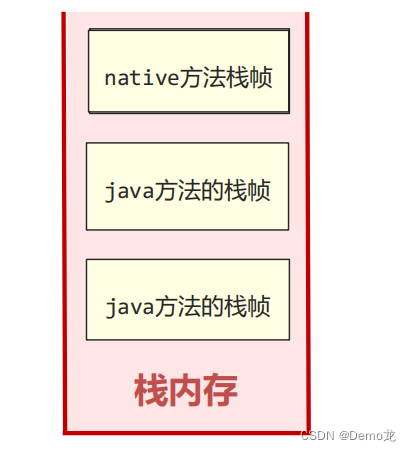
JVM——运行时数据区(程序计数器+栈)
目录 1.程序计数器2.栈Java虚拟机栈 - 栈帧的组成1.Java虚拟机栈-局部变量表3.Java虚拟机栈-操作数栈3.Java虚拟机栈-帧数据 3.Java虚拟机栈-栈内存溢出4.本地方法栈 ⚫ Java虚拟机在运行Java程序过程中管理的内存区域,称之为运行时数据区。 ⚫ 《Java虚拟机规范》中…...
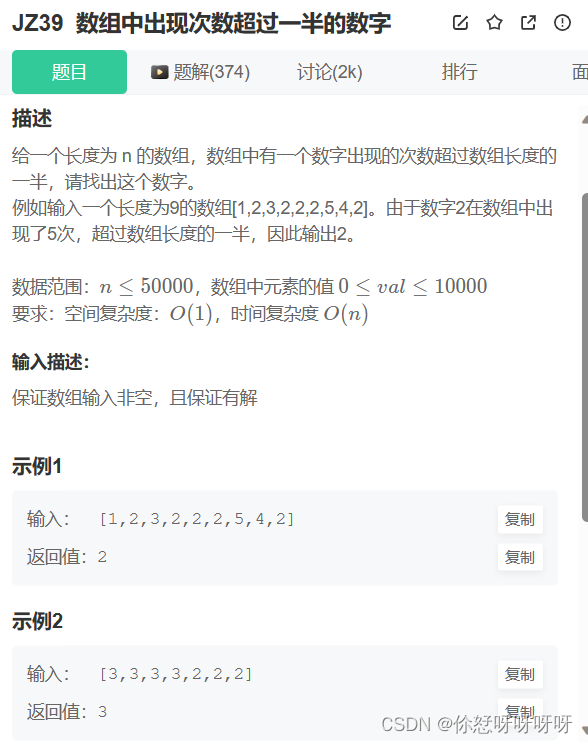
【C++】数组中出现次数超过一半的数字
代码: class Solution { public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * param numbers int整型vector * return int整型*/int MoreThanHalfNum_Solution(vector<int>& numbers) {int …...
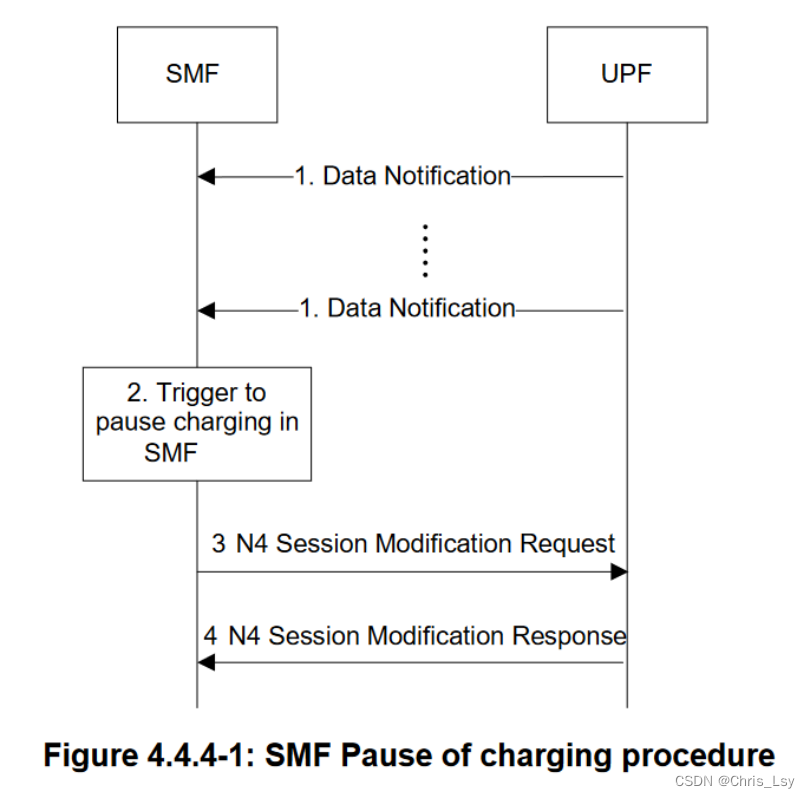
3GPP协议解读(一)_23.501_23.502_PDU Session_SMF与UDP的交互
UE发起计算服务申请后,网络侧处理的流程 UE发起服务的流程:service request网络侧处理服务涉及的通信数据通过PDU Session进行传输,涉及到SMF与UPF的交互。PDU Session的建立、管理全部由SMF(Session Management Function&#x…...

天池2023智能驾驶汽车虚拟仿真视频数据理解--baseline
baseline 代码 代码 百度飞浆一键运行 import paddle from PIL import Image from clip import tokenize, load_model import glob, json, os import cv2 from PIL import Image from tqdm import tqdm_notebook import numpy as np from sklearn.preprocessing import norma…...
C++入门(1)—命名空间、缺省参数
目录 一、什么是C 1、C关键字(C98) 2、C兼容C 二、C程序预处理指令 三、命名空间 1、命名冲突 第一种: 第二种: 2、域作用限定符 3、实现命名空间 4、命名空间冲突 5、访问命名空间 6、命名空间“std” 四、输入输出 1、定义 2、自动识…...

以程序员的身份使用curl获取速卖通详情
作为一名程序员,我们经常需要和各种API接口打交道。在电商领域,速卖通是一个非常受欢迎的平台。本文将介绍如何使用curl工具通过速卖通的API接口获取商品详情。 一、准备工作 在开始之前,请确保您已完成以下准备工作: 注册速卖…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
