存钱虚拟计划,嘚
存钱计划—虚拟
2024年 (第一年)
1月 2月 3月 4月 5月 6 月 7月 8月 9月 10月 11月 12月
1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w
2025年(第二年)
1w+1w*102.5% A 懒得写A代替 A A A A A A A A A A
2026年(第三年)
(1w+1w*102.5)*102.5%+1w A 懒得写A代替 A A A A A A A A A A
2027年(第4年)
((1w+1w*102.5)*102.5%+1w ) *102.5%. +1w
2028年(第5年)
(((1w+1w*102.5)*102.5%+1w ) *102.5% +1w )*102.5%+1w
2029年(第6年)
((((1w+1w*102.5)*102.5%+1w ) *102.5% +1w )*102.5%+1w )*102.5%+1w
2030年(第7年)
(((((1w+1w*102.5)*102.5%+1w ) *102.5% +1w )*102.5%+1w )*102.5%+1w) *102.5% +1w
上述没有错吧,那么来个公式
S 总资产={ (((((1w+1w*102.5)*102.5%+1w ) *102.5% +1w )*102.5%+1w )*102.5%+1w) *102.5% +1w }*12
S 总资产/12=((((1w+1w*102.5%)*102.5%+1w ) *102.5% +1w )*102.5%+1w )*102.5%^2+1w*102.5%
=(((1w+1w*102.5%)*102.5%+1w ) *102.5% +1w )*102.5%*^3+1w *102.5%^2+1w*102.5%
=((1w+1w*102.5%)*102.5%+1w ) *102.5%*^4 +1w *102.5%*^3+1w *102.5%^2+1w*102.5%
=(1w+1w*102.5%)*102.5%*^5+1w *102.5%*^4+1w *102.5%*^3+1w *102.5%^2+1w*102.5%
=1w*102.5%*^6+1w*102.5%*^5+1w *102.5%*^4+1w *102.5%*^3+1w *102.5%^2+1w*102.5%
= 1w*(102.5*^6+102.5*^5+102.5*^4+102.5*^3+102.5*^2+102.5*^2+102.5*0)
等比数列公式
Sn=a1(1-q^n)/(1-q)(q≠1)
S 总资产/12= 1w*(1*1-1.025^7)/1-1.025
然后 月存款基数 T=1w. 一年定期复利 k=1.025(也是年利率2.5%) 存款年限Y=7
S 总资产/12= T*(1-k^Y)/1-K = T*(k^Y-1)/k-1
第Y+1年到靠利息活着,存本取息(低消费支出)》2K. 代表R
每个月的钱利息就是 T*(k^Y-1)/(k-1) *(k-1)
T*(k^Y-1)/(k-1) *(k-1)>=2000
再次反项目带入
T*(k^Y-1)>=R. =>. K^y-1>= R/T.=>1.025^y-1>= 0.2
再下面的计算结果 如果K 是1.025.
1.025的1次方的值1.025
1.025的2次方的值1.050625
1.025的3次方的值1.0768906249999997
1.025的4次方的值1.1038128906249995
1.025的5次方的值1.1314082128906244
1.025的6次方的值1.15969341821289
1.025的7次方的值1.1886857536682123
1.025的8次方的值1.2184028975099173
1.025的9次方的值1.2488629699476652
1.025的10次方的值1.2800845441963566
1.025的11次方的值1.3120866578012655
1.025的12次方的值1.344888824246297
1.025的13次方的值1.3785110448524542
1.025的14次方的值1.4129738209737654
1.025的15次方的值1.4482981664981096
1.025的16次方的值1.4845056206605622
1.025的17次方的值1.521618261177076
1.025的18次方的值1.5596587177065029
1.025的19次方的值1.5986501856491653
1.025的20次方的值1.6386164402903942
1.025的21次方的值1.679581851297654
1.025的22次方的值1.7215713975800953
1.025的23次方的值1.7646106825195975
1.025的24次方的值1.8087259495825871
1.025的25次方的值1.8539440983221518
1.025的26次方的值1.9002927007802053
1.025的27次方的值1.9478000182997104
1.025的28次方的值1.996495018757203
1.025的29次方的值2.046407394226133
1.025的30次方的值2.097567579081786
1.025的31次方的值2.15000676855883
1.025的32次方的值2.203756937772801
1.025的33次方的值2.258850861217121
1.025的34次方的值2.3153221327475486
1.025的35次方的值2.373205186066237
1.025的36次方的值2.432535315717893
1.025的37次方的值2.49334869861084
1.025的38次方的值2.555682416076111
1.025的39次方的值2.6195744764780136
1.025的40次方的值2.685063838389963
1.025的41次方的值2.7521904343497123
1.025的42次方的值2.8209951952084547
1.025的43次方的值2.891520075088666
1.025的44次方的值2.9638080769658823
1.025的45次方的值3.0379032788900293
1.025的46次方的值3.1138508608622795
1.025的47次方的值3.1916971323838363
1.025的48次方的值3.271489560693432
1.025的49次方的值3.3532767997107675。 这是干了50年的
所以通过以上结论, 如果你想每个月靠利息2千生存,每月存一万你需要8年
再来看
如果幸福指数分1-10个等级 =R/T*10
1-3基本幸福。
3-5非常幸福
4-7 超级幸福
7-10 幸福的没边了
如果幸福系数(H)那么 H= R/T*10的值
如果H越大你越幸福 那么让H变大 就代表分子越小越好,那么就是。 T*10越小越好, T代表你每月存的金额。
那么通俗讲。 就是你每月存款为零, H就是无穷大(别反驳——你想想每个月你月光你是多快乐)
——————————————————所以,存个嘚得钱,嗨起来这里。 越存越痛苦
再说一种极端的情况。
就是银行存款利率为零
公式 就是这样的 K^y-1> R/T=》1^Y-1>R/T=>0>R/T. 等式永远不成立了
所以说银行利率越低的时候,你存钱,你就越痛苦,花的越少你就越痛苦。
所以,存个嘚得钱,别存了嗨起来
以上发言全当一乐,别较真(因为这个社会是公平的,货币出现的那一刻所有人都成为他的奴隶,不管是贪婪的资本,还是劳苦的大众,芸芸众生皆平等,不平等的是人心。这也许就是云动还是风动吧)
相关文章:

存钱虚拟计划,嘚
存钱计划—虚拟 2024年 (第一年) 1月 2月 3月 4月 5月 6 月 7月 8月 9月 10月 11月 12月 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 2025年(第二年) 1w1w*102.5% A 懒得写A代替 A A A A A A A A A A 2026年(第三年) (1w1w*10…...
基于IDEA进行Maven工程构建
Java全能学习面试指南:https://javaxiaobear.cn 1. 构建概念和构建过程 项目构建是指将源代码、依赖库和资源文件等转换成可执行或可部署的应用程序的过程,在这个过程中包括编译源代码、链接依赖库、打包和部署等多个步骤。 项目构建是软件开发过程中…...
Openssl X509 v3 AuthorityKeyIdentifier实验与逻辑分析
Openssl是X509的事实标准,目前主流OS或个别安全性要求较高的设计场景,对X509的证书链验证已经不在停留在只从数字签名校验了,也就是仅仅从公钥验签的角度,在这些场景中,往往还会校验AuthorityKeyIdentifier和SubjectKe…...

聊聊logback的MDCFilter
序 本文主要研究一下logback的MDCFilter MatchingFilter ch/qos/logback/classic/turbo/MatchingFilter.java public abstract class MatchingFilter extends TurboFilter {protected FilterReply onMatch FilterReply.NEUTRAL;protected FilterReply onMismatch FilterR…...
Windows10安装麒麟桌面V10双系统
概述 想要在Windows10操作系统中安装麒麟V10的桌面操作系统(Kylin-Desktop-V10-Professional-Release-Build1-210203-X86_64) 安装前准备 1、先搞清楚自己的电脑类型 A MBR传统bios单硬盘 B MBR 传统bios双硬盘(SSD固态硬盘机械硬盘&…...

file_put_contents锁的问题
记一次线上生产file_put_contents锁的问题 php项目,很多地方加了日志记录,方法为 function logstr($namelog,$str"",$type"Ymd"){$file date("$type")._.$name..log;$add __DIR__./../runtime/cuslog/.date("Ym&q…...
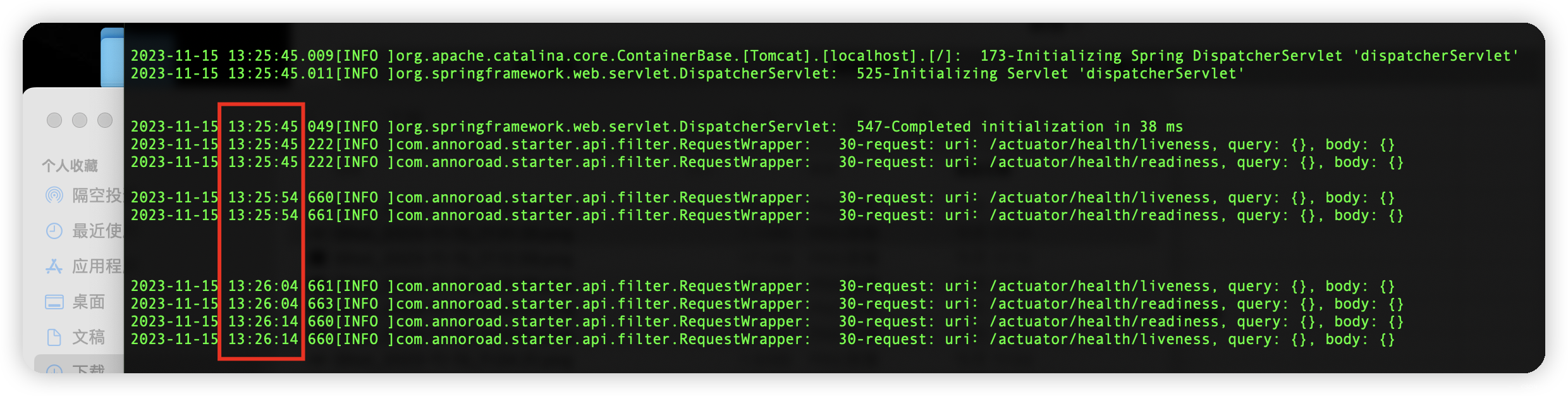
工作中积累的对K8s的就绪和存活探针的一些认识
首先,我的项目是基于 Spring Boot 2.3.5 的,并依赖 spring-boot-starter-actuator 提供的 endpoints 来实现就绪和存活探针,POM 文件如下图: 下面,再让我们来看下与该项目对应的Deployment的YAML文件,如下…...

什么是会话固定以及如何在 Node.js 中防止它
什么是会话固定以及如何在 Node.js 中防止它 在深入讨论之前,我们需要了解会话是什么以及会话身份验证如何工作。 什么是会话? 正如我们所知,HTTP 请求是无状态的,这意味着当我们发送登录请求时,并且我们有有效的用…...

代码随想录算法训练营第五十二天|300. 最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
第九章 动态规划part13 300. 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数…...

使用 Hugging Face Transformer 微调 BERT
微调 BERT有助于将其语言理解能力扩展到更新的文本领域。BERT 的与众不同之处在于它能够掌握句子的上下文关系,理解每个单词相对于其邻居的含义。我们将使用 Hugging Face Transformers 训练 BERT,还将教 BERT 分析 Arxiv 的摘要并将其分类为 11 个类别之一。 为什么微调 BER…...

Vue原型对象
原型对象 prototype 称为:显示的原型属性,用法:函数.prototype,例如:Vue.prototype __proto__称为:隐式的原型属性,用户:实例.proto,例如:vm.proto 不管如何 …...

向量数据库的分类概况
保存和检索矢量数据的五种方法: 像 Pinecone 这样的纯矢量数据库 全文搜索数据库,例如 ElasticSearch 矢量库,如 Faiss、Annoy 和 Hnswlib 支持矢量的NoSQL 数据库,例如 MongoDB、Cosmos DB 和 Cassandra 支持矢量的SQL 数据库&am…...

工业镜头的类别
工业镜头的类别 按照等效焦距分为: 广角镜头 中焦距镜头 长焦距镜头 广角镜头 等效焦距小于标准镜头(等效焦距为50mm)的镜头。特点是最小工作距离短,景深大,视角大。常常表现为桶形畸变。 中焦距镜头 焦距介于广角镜…...

实验11 SQL互联网业务查询-2
这就是SQL题带给我的自信😕 可能发题解到博客上,主要是写完一遍实在不想看第二遍,太长了,优化都不想优化,看着头疼。 技术栈 – WhiteNights Site 一 USE mydata; #请在此处添加实现代码 ########## Begin #######…...

C++知识点梳理:C++ templates
c模板包括:类模板、类(非模板类和模板类)方法模板、函数模板、别名模板、变量模板。 类模板模板参数列表说明: 1)类定义 仅模板参数列表声明,template<>行。 类名后无需参数说明<>。 2…...
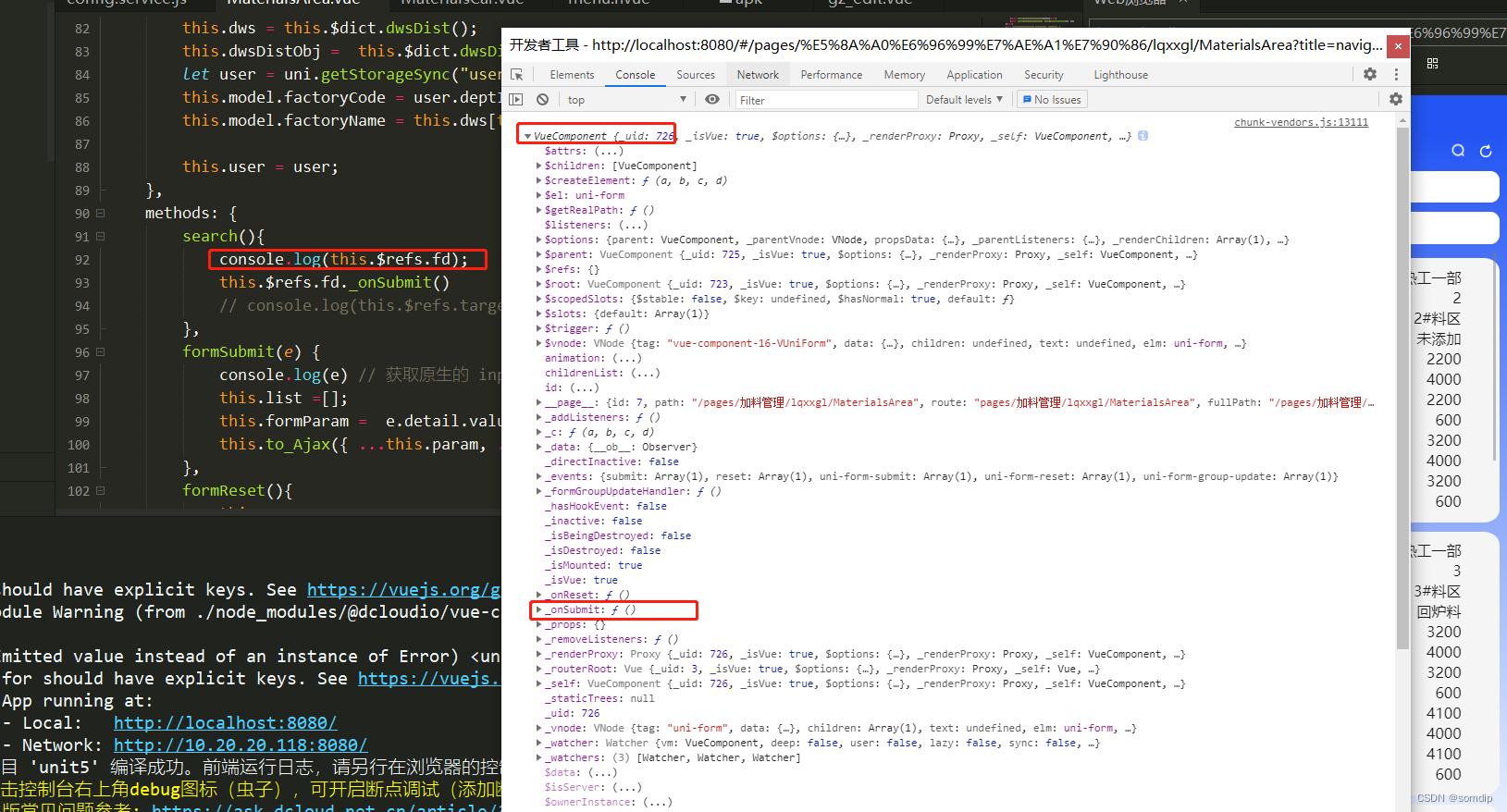
uniapp form表单提交事件手动调用
背景: UI把提交的按钮弄成了图片,之前的button不能用了。 <button form-type"submit">搜索</button> 实现: html: 通过 this.$refs.fd 获取到form的vue对象。手动调用里面的_onSubmit()方法。 methods:…...

Accelerate 0.24.0文档 三:超大模型推理(内存估算、Sharded checkpoints、bitsandbytes量化、分布式推理)
文章目录 一、内存估算1.1 Gradio Demos1.2 The Command 二、使用Accelerate加载超大模型2.1 模型加载的常规流程2.2 加载空模型2.3 分片检查点(Sharded checkpoints)2.4 示例:使用Accelerate推理GPT2-1.5B2.5 device_map 三、bitsandbytes量…...
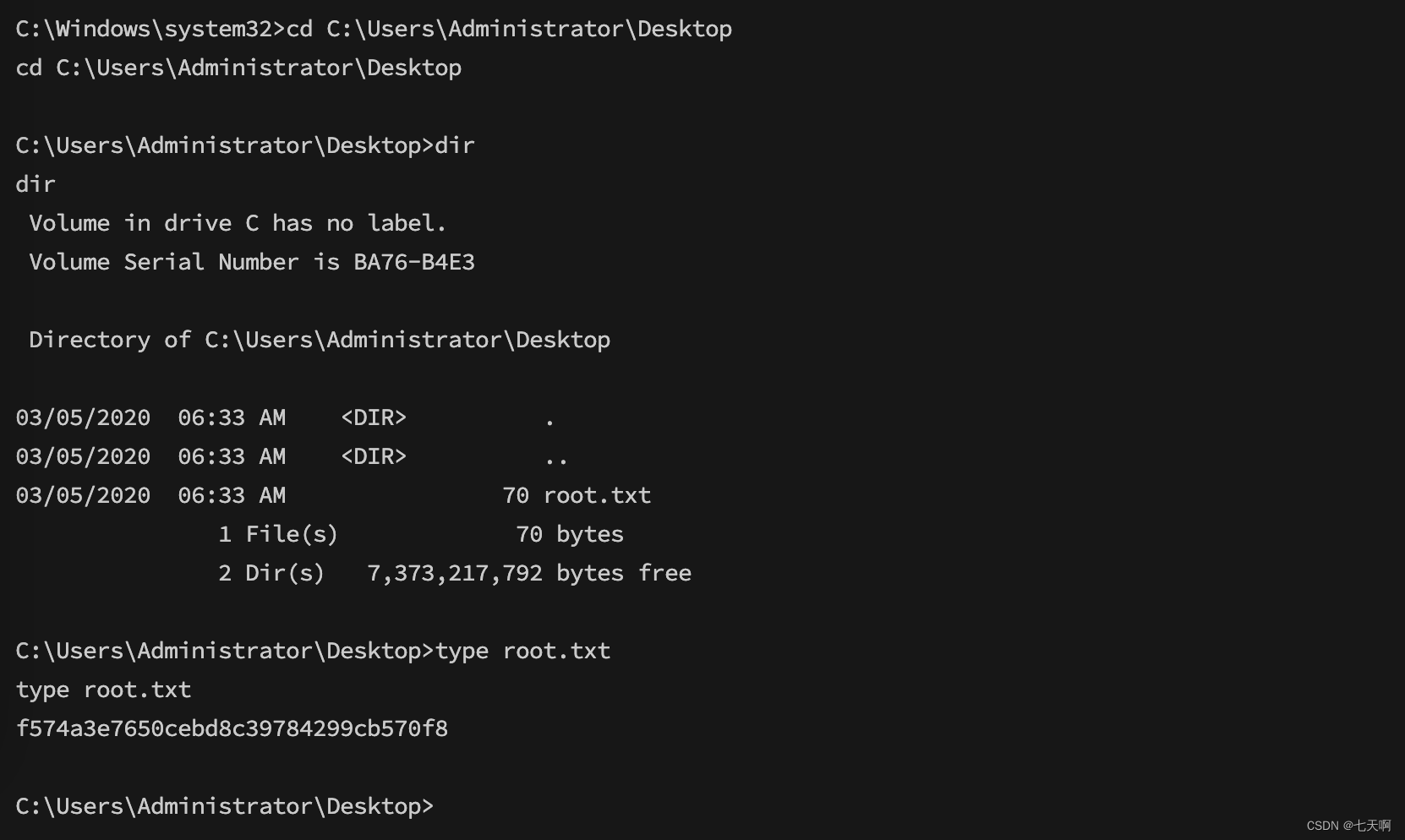
HackTheBox-Starting Point--Tier 2---Markup
文章目录 一 Markup测试过程1.1 打点1.2 权限获取1.3 权限升级 二 题目 一 Markup测试过程 1.1 打点 1.端口扫描 nmap -A -Pn -sC 10.129.95.1922.访问web网站,登录口爆破发现存在弱口令admin:password 3.抓包,发现请求体是XML格式 4.尝试使…...
android studio导入eclipse项目
网上下载一个老工程,.project文件里有eclipse。 android studio导入eclipse项目 eclipse项目结构 Android studio文件结构 下面是导入步骤: 第一步,打开一个项目。 选择File->New->Import Project 第二步,选择Eclipse项目根…...

如何利用AI实现银行存量客户的营销?
近年来,大数据、人工智能等热门关键字多次被写入中央文件与国务院政府工作报告,目前已上升为国家战略,并将深刻地改变现有行业的游戏规则。 金融行业是当今大数据、人工智能应用最广、最深的领域之一。随着数据仓库和数据科学的发展ÿ…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
