图论与网络优化2
CSDN 有字数限制,因此笔记分别发布,目前:
- 【笔记1】概念与计算、树及其算法
- 【笔记2】容量网络模型
4 最大流及其算法
4.1 容量网络模型
4.1.1 容量网络
容量网络:如果一个加权有向网络 D D D 满足如下三个条件:①存在唯一一个入度为 0 0 0 的顶点,称为源;②存在唯一一个出度为 0 0 0 的顶点,称为汇;③每条弧 ( v i , v j ) (v_i,v_j) (vi,vj) 赋权 c i j c_{ij} cij 是一个非负数,称为弧 ( v i , v j ) (v_i,v_j) (vi,vj) 的容量,则把这个加权有向网络 D D D 称为容量网络。
4.1.2 流
流:设 D D D 是一个容量网络,令 c i j c_{ij} cij 表示弧 ( v i , v j ) (v_i,v_j) (vi,vj) 的容量。设 f f f 是定义在 D D D 的弧集上的一个函数,它赋予每条弧 ( v i , v j ) (v_i,v_j) (vi,vj) 一个非负实数 f i j f_{ij} fij,若 f f f 满足:① f i j ≤ c i j f_{ij} \leq c_{ij} fij≤cij;② ∀ v j ∈ V ( D ) \forall v_j \in V(D) ∀vj∈V(D) \ { v s , v t } \{v_s,v_t\} {vs,vt} 有 ∑ ( v i , v j ) ∈ E ( D ) f i j = ∑ ( v j , v i ) ∈ E ( D ) f j i \sum_{(v_i,v_j)\in E(D)} f_{ij} = \sum_{(v_j,v_i)\in E(D)} f_{ji} ∑(vi,vj)∈E(D)fij=∑(vj,vi)∈E(D)fji,则称 f f f 为容量网络 D D D 的一个流,称 f i j f_{ij} fij 为弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上的流量。
(非)饱和弧:弧上的流量(未)达到弧的容量。
4.1.3 流值
定理:设 f f f 是容量网络 D D D 的一个流,其中源为 v s v_s vs,汇为 v t v_t vt,由源的流出量等于汇的流入量,即 ∑ ( v s , v j ) ∈ E ( D ) f s i = ∑ ( v i , v t ) ∈ E ( D ) f i t \sum_{(v_s,v_j)\in E(D)}f_{si}=\sum_{(v_i,v_t)\in E(D)}f_{it} ∑(vs,vj)∈E(D)fsi=∑(vi,vt)∈E(D)fit
证明:注意到每条弧上的流量,既是其头顶点的流入量,也是其尾顶点的流出量,因此所有弧上的流量之和、所有顶顶啊的流入量之和、所有顶点的流出量之和,这三者相等。
流值:设 f f f 是容量网络 D D D 的一个流,其源为 v s v_s vs,汇为 v t v_t vt,称源的流出量为流 f f f 的流值,记作 v a l ( f ) val(f) val(f)。
4.1.4 最大流
最大流:设 D D D 是一个容量网络,若 f f f 是 D D D 上流值最大的流,则把 f f f 称为 D D D 的最大流。
截:设 D D D 是一个容量网络,源为 v s v_s vs,汇为 v t v_t vt。设顶点子集 S ⊂ V ( D ) , S ‾ = V ( D ) S \subset V(D),\overline{S}=V(D) S⊂V(D),S=V(D) \ S S S,且 v s ∈ S , v t ∈ S ‾ v_s\in S, v_t \in \overline{S} vs∈S,vt∈S,则称弧集 { ( v i , v j ) ∈ E ( D ) ∣ v i ∈ S , v j ∈ S ‾ } \{(v_i,v_j)\in E(D)|v_i \in S, v_j \in \overline{S}\} {(vi,vj)∈E(D)∣vi∈S,vj∈S} 为容量网络 D D D 的截,记作 ( S , S ‾ ) (S,\overline{S}) (S,S)。
截的容量: ∑ ( v i , v j ) ∈ ( S , S ‾ ) c i j \sum_{(v_i,v_j)\in(S,\overline{S})}c_{ij} ∑(vi,vj)∈(S,S)cij,记作 c ( S , S ‾ ) c_(S,\overline{S}) c(S,S)。
最小截:容量达最小的截为最小截。
定理:设 D D D 是一个容量网络,源为 v s v_s vs,汇为 v t v_t vt。设 f f f 是容量网络 D D D 的一个流, ( S , S ‾ ) (S,\overline{S}) (S,S) 是 D D D 的一个截,则有 v a l ( f ) ≤ c ( S , S ‾ ) val(f) \leq c(S,\overline{S}) val(f)≤c(S,S)。
证明:…
流值与截容量相等当且仅当每条弧都是饱和弧且无逆流的时候。
若容量网络的一个流 f f f 的流值等于某个截 ( S , S ‾ ) (S,\overline{S}) (S,S)的容量,即 c ( S , S ‾ ) = v a l ( f ) c(S,\overline{S})=val(f) c(S,S)=val(f),则 f f f 为最大流, ( S , S ‾ ) (S,\overline{S}) (S,S) 为最小截。
4.2 最大流算法
4.2.1 可增路
可增路:设 P P P 是一条 ( v s , v j ) (v_s,v_j) (vs,vj) 路,如果①对 P P P 中每条正向弧 ( v i , v j ) , f i j < c i j (v_i,v_j),f_{ij} < c_{ij} (vi,vj),fij<cij;②对 P P P 中每条反向弧 ( v i , v j ) , f i j > 0 (v_i,v_j),f_{ij} > 0 (vi,vj),fij>0,则称 ( v s , v j ) (v_s,v_j) (vs,vj) 为 f f f 非饱和路;否则为饱和路。从源到汇的 f f f 非饱和路,称为 f f f 可增路。
4.2.2 最大流算法
定理:设容量网络 D D D 的源为 v s v_s vs,汇为 v t v_t vt, f f f 为 D D D 的一个流,则 f f f 为最大流当且仅当 D D D 中不存在 f f f 可增路。
证明:只需证明充分性。只需证明存在截 ( S , S ‾ ) (S,\overline{S}) (S,S) 满足: ( S , S ‾ ) (S,\overline{S}) (S,S) 中的每条弧都是饱和弧, ( S ‾ , S ) (\overline{S}, S) (S,S) 中的每条弧都是零弧。
将顶点分类,令 S = { v s } ∪ { v j ∣ 存在一条 f 非饱和路 ( v s , v j ) } S=\{v_s\} \cup \{v_j|存在一条 f 非饱和路 (v_s,v_j)\} S={vs}∪{vj∣存在一条f非饱和路(vs,vj)},故有 v t ∈ S ‾ v_t \in \overline{S} vt∈S 。
则 S S S 与 S ‾ \overline S S 之间假设 f i j < c i j f_{ij} < c_{ij} fij<cij,易见 P + ( v i , v j ) P+(v_i,v_j) P+(vi,vj) 亦为 f f f 非饱和路,与 v j ∈ S ‾ v_j \in \overline{S} vj∈S 矛盾。同理可以证明 f i j = 0 f_{ij}=0 fij=0。
标号法能求解可增路
4.2.3 最大流最小截定理
最大流算法结束时,最大流流值等于最小截容量。
定理:在任何容量网络 D D D 中,最大流的流值等于最小截的容量。
证明:(大致思路)设 S S S 为能用标号法能够获得标号的顶点集合,则 ( S , S ‾ ) (S,\overline{S}) (S,S) 之间的弧的值必定为 0 0 0。
4.3 最小费用最大流
4.3.1 问题描述
流 f f f 的费用:设容量网络 D D D 的源为 v s v_s vs,汇为 v t v_t vt, c i j c_{ij} cij 和 b i j b_{ij} bij 分别表示弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上的容量和单位流量费用,设 f f f 是 G G G 的流,则称 b ( f ) = ∑ ( v i , v j ) ∈ E ( D ) f i j b i j b(f)=\sum_{(v_i,v_j)\in E(D)}f_{ij}b_{ij} b(f)=∑(vi,vj)∈E(D)fijbij 为流 f f f 的费用。在容量网络 D D D 的所有最大流中寻找费用最小的流,这样的流称为最小费用最大流。
4.3.2 F增广圈
增广圈:设 Q Q Q 是一个具有指定正向的圈, Q + Q^+ Q+ 为圈 Q Q Q 上正向弧的集合, Q − Q^- Q− 为圈 Q Q Q 上反向弧的集合。
- δ i j = c i j − f i j , ( v i , v j ) ∈ Q + \delta_{ij}=c_{ij}-f_{ij},(v_i,v_j) \in Q^+ δij=cij−fij,(vi,vj)∈Q+
- δ i j = f i j , ( v i , v j ) ∈ Q − \delta_{ij}=f_{ij},(v_i,v_j) \in Q^- δij=fij,(vi,vj)∈Q−。
δ ( Q ) = m i n { δ i j ∣ ( v i , v j ) ∈ E ( Q ) } \delta(Q)=min\{\delta_{ij}|(v_i,v_j) \in E(Q)\} δ(Q)=min{δij∣(vi,vj)∈E(Q)}。
若 δ ( Q ) > 0 \delta(Q)>0 δ(Q)>0,则称 δ ( Q ) \delta(Q) δ(Q) 为允许修改流量,称圈 Q Q Q 为容量网络 D D D 上关于流 f f f 的增广圈。
对于 f f f 增广圈 Q Q Q,我们可以定义 f ′ f' f′:
- f i j ′ = f i j + δ ( Q ) , ( v i , v j ) ∈ Q + f_{ij}^{'}=f_{ij} + \delta(Q),(v_i,v_j)\in Q^+ fij′=fij+δ(Q),(vi,vj)∈Q+
- f i j ′ = f i j − δ ( Q ) , ( v i , v j ) ∈ Q − f_{ij}^{'}=f_{ij} - \delta(Q),(v_i,v_j)\in Q^- fij′=fij−δ(Q),(vi,vj)∈Q−
- f i j , ( v i , v j ) ∉ E ( Q ) f_{ij},(v_i,v_j) \notin E(Q) fij,(vi,vj)∈/E(Q)
这样 f ′ f' f′ 仍是 D D D 的流并且 v a l ( f ′ ) = v a l ( f ) val(f')=val(f) val(f′)=val(f),称 f ′ f' f′ 为基于 f f f 增广圈 Q Q Q 的修正流。
负圈:设有容量网络 D D D, f f f 是一个流, f i j , c i j , b i j f_{ij},c_{ij},b_{ij} fij,cij,bij 分别为弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上的流量、容量和单位费用,设 Q Q Q 是关于流 f f f 的增广圈。称 b ( Q , f ) = ∑ ( v i , v j ) ∈ Q + b i j − ∑ ( v i , v j ) ∈ Q − b i j b(Q,f)=\sum_{(v_i,v_j)\in Q^+}b_{ij}-\sum_{(v_i,v_j)\in Q^-}b_{ij} b(Q,f)=∑(vi,vj)∈Q+bij−∑(vi,vj)∈Q−bij 为增广圈的费用,若小于 0 0 0,则称 Q Q Q 为负圈。负圈与流量、容量、费用、圈的指定方向有关。
4.3.3 Klein 算法
算法:
- 求容量网络 D D D 的一个最大流。
- 寻找网络中的负圈。若没有负圈,算法结束;若找到一个负圈,转step 3
- 修改负圈 Q Q Q 上各弧的流量,得到修正流。在新修正流的基础上,转step 2,继续寻找负圈。
定理:设有容量网络 D D D, f f f 是一个流, f i j , c i j , b i j f_{ij},c_{ij},b_{ij} fij,cij,bij 分别为弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上的流量、容量和单位费用,则 f f f 是最小费用最大流当且仅当任何 f f f 增广圈 Q Q Q 的费用 b ( Q , f ) ≥ 0 b(Q,f)\geq0 b(Q,f)≥0,即无负圈。
5 遍历性及其算法
5.1 Euler图和有向Euler图
5.1.1 定义
Euler图:如果图 G G G 中存在包含所有边的闭迹 W W W,则称 G G G 为 E u l e r Euler Euler 图, W W W 称为 G G G 的 E u l e r Euler Euler 闭迹。
半Euler图:如果图 G G G 中存在包含所有边的迹 P P P,则称 G G G 为 半 E u l e r 半Euler 半Euler 图, P P P 称为 G G G 的 E u l e r Euler Euler 迹。
定理:设 G G G 为非空连通图,则下面三个命题等价:
- G G G 是 E u l e r Euler Euler 图;
- G G G 中不含奇点;
- G G G 可以表示为若干个没有公共边的圈的并。
证明:
- 1->2:设 G G G 是连通的 E u l e r Euler Euler 图, W W W 是 G G G 的 E u l e r Euler Euler 闭迹,则 ∀ v ∈ V ( G ) , v \forall v \in V(G),v ∀v∈V(G),v 必定在 W W W 中出现,当 v v v 作为内部点,每出现一次,必定与 G G G 中两条边关联;当 v v v 作为 W W W 的起点,则 v v v 也是重点,从而它必与两条边关联,因此 G G G 的每个顶点都是偶点。
- 2->3:设 G G G 是非空连通图且不含奇点,则 G G G 不是树,从而 G G G 中含有圈,不断取出圈来得到新图再取圈,因此可以从第二个命题演变成第三个命题。
- 3->1:由 E u l e r Euler Euler 图的定义,结论显然。
有向Euler图:若有向图 D D D 中存在包含所有弧的有向闭迹,则称 D D D 为有向 E u l e r Euler Euler 图,这样的有向闭迹,称为 D D D 的有向 E u l e r Euler Euler 闭迹。
有向半Euler图:若有向图 D D D 中存在包含所有弧的有向迹,则称 D D D 为有向 E u l e r Euler Euler 图,这样的有向迹,称为 D D D 的有向 E u l e r Euler Euler 迹。
定理:设 G G G 为非空连通有向图,则下面三个命题等价:
- D D D 是有向 E u l e r Euler Euler 图;
- ∀ v ∈ V ( D ) \forall v \in V(D) ∀v∈V(D),有 d + ( v ) = d − ( v ) d^+(v)=d^-(v) d+(v)=d−(v)
- G G G 可以表示为弧不交的回路的并。
5.1.2 Fleury 算法
算法思想:从任意顶点出发,除非别无选择,否则总是选择一条不是割边的且没走过的边,直到获得 E u l e r Euler Euler 闭迹为止。
定理:设 G G G 是 E u l e r Euler Euler 图, W = v 0 e 1 v 1 . . . e n v n W=v_0e_1v_1...e_nv_n W=v0e1v1...envn 是 F l e u r y Fleury Fleury 算法结束时得到的迹,则 W W W 一定是图 G G G 的 E u l e r Euler Euler 闭迹。
证明:…
5.1.3 编码盘设计
例题:16个二进制数应该如何排列,使得圆盘沿顺时针旋转一部分,恰好组成 0000 0000 0000 到 1111 1111 1111 的 16 16 16 组四位二进制输出,同时旋转一周又返回到 0000 0000 0000 状态?
答案:定义一个有 8 8 8 个顶点的有向图 D D D,其中顶点用 3 3 3 维 0 − 1 0-1 0−1 序列 x 1 x 2 x 3 x_1x_2x_3 x1x2x3 标记,且顶点 x 1 x 2 x 3 x_1x_2x_3 x1x2x3 与顶点 x 2 x 3 0 , x 2 x 3 1 x_2x_30,x_2x_31 x2x30,x2x31 以出弧的形式相连,这样得到的有向图 D D D 中,每个顶点的入度和出度相等,都等于 2 2 2。然后从 000 000 000 出发,可以得到一个有向 E u l e r Euler Euler 闭迹为 …。注意起终点重复,所以序列取末尾数字,得…
该问题可以扩展,得到的有向图为德布鲁英图 B ( 2 , n ) B(2,n) B(2,n)。每个顶点最后一位数字构成序列为 德布鲁英序列。

5.2 中国邮递员问题
5.2.1 问题描述
管梅谷教授提出并研究了中国邮递员问题。
问题内容:在加权连通图 G G G 中,寻找一条经过每条边至少一次且权和最小的闭迹,即 G G G 的最优环游。
思考角度:对于重复走的边,可以看作为两点之间的重边(即重复走的边视为 k k k 重边)。
5.2.2 奇偶点图上作业法
最优环游的奇偶点图上作业法:
- 把图 G G G 所有奇点配成对,将每对奇点之间的一条链的每条边改为二重边,得到一个新图 G 1 G_1 G1,图中没有奇点
- 在图 G 1 G_1 G1 中,若顶点之间有 k ( k ≥ 3 ) k(k\geq3) k(k≥3) 重边,则去掉其中偶数条,只保留 1 / 2 1/2 1/2 条边,得到图 G 2 G_2 G2。
- 检查 G 2 G_2 G2 中的每一个圈 C C C,若重复边的权和超过此圈权和的一半,则重边变为单边,单边变为二重边,重复这一过程,直到所有圈上重边的权和都不超过圈权和一半,得到 G 3 G_3 G3。
- 用 F l e u r y Fleury Fleury 算法求 G 3 G_3 G3 的 E u l e r Euler Euler 闭迹,得到图 G G G 的最优环游
定理:设 G G G 是加权连通图,则奇偶点图上作业法得到的闭途径是最优环游。
证明:…
例题:

答案:图 G G G 中有 6 6 6 个奇点 v 2 , v 3 , v 5 , v 8 , v 10 , v 11 v_2,v_3,v_5,v_8,v_{10},v_{11} v2,v3,v5,v8,v10,v11,将它们搭配成三对,因此添加 v 2 v 3 v 4 v 5 , v 3 v 2 v 1 v 8 , v 10 v 11 v_2v_3v_4v_5,v_3v_2v_1v_8,v_{10}v_{11} v2v3v4v5,v3v2v1v8,v10v11。注意 v 2 v 3 v_2v_3 v2v3 间有两条新添加的边,删去得到新图。

v 1 v 2 v 7 v 8 v 1 , v 3 v 4 v 5 v 6 v 3 v_1v_2v_7v_8v_1,v_3v_4v_5v_6v_3 v1v2v7v8v1,v3v4v5v6v3 中非最优添边,因此重边变单边,单边变重边,再次得到新图:

再检查圈 v 2 v 3 v 6 v 11 v 10 v 7 v 2 v_2v_3v_6v_{11}v_{10}v_7v_2 v2v3v6v11v10v7v2,也非最优,执行单重边置反,得到新图。

检查通过,执行 F l e u r y Fleury Fleury 算法,得到最优环游为:
v 1 v 2 v 3 v 2 v 7 v 8 v 7 v 6 v 5 v 6 v 11 v 12 v 5 v 4 v 3 v 6 v 11 v 10 v 7 v 10 v 9 v 8 v 1 v_1v_2v_3v_2v_7v_8v_7v_6v_5v_6v_{11}v_{12}v_5v_4v_3v_6v_{11}v_{10}v_7v_{10}v_9v_8v_1 v1v2v3v2v7v8v7v6v5v6v11v12v5v4v3v6v11v10v7v10v9v8v1,环游总长度 109 109 109。
相关文章:

图论与网络优化2
CSDN 有字数限制,因此笔记分别发布,目前: 【笔记1】概念与计算、树及其算法【笔记2】容量网络模型 4 最大流及其算法 4.1 容量网络模型 4.1.1 容量网络 容量网络:如果一个加权有向网络 D D D 满足如下三个条件:①…...

ES Kibana windows 安装
ES & Kibana windows 安装 声明: 本文没有实际操作过,只记录。具体操作请参考 ES & Kibana 安装 该文章 JDK1.8,最低要求!ElasticSearch客户端,界面工具! Java开发,ElasticSearch的版…...
分布式事务seata的使用
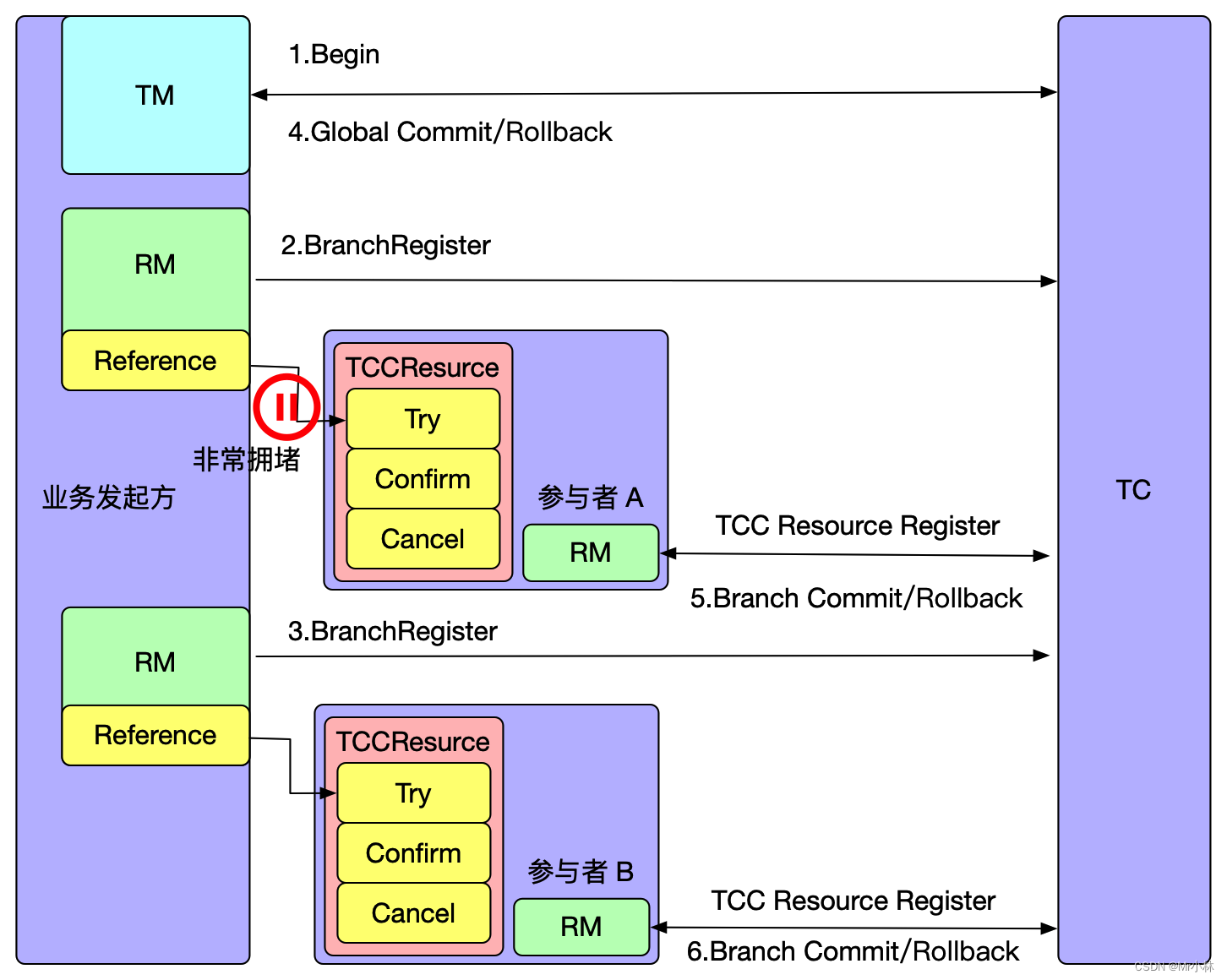
分布式事务介绍 在微服务架构中,完成某一个业务功能可能需要横跨多个服务,操作多个数据库。这就涉及到到了分布式事务,需要操作的资源位于多个资源服务器上,而应用需要保证对于多个资源服务器的数据操作,要么全部成功&…...
使用宝塔面板安装mysql
1.第一步 在官网https://www.bt.cn/new/download.html下载页面直接在服务器控制面板复制这里的代码下载即可 2.第二步 下载好后按照服务器面版上有个公网地址,含有用户名和密码,保存好,然后通过公网地址打开一个网页,绑定自己注册…...

Flink 支持三种时间语义
在 Apache Flink 中,时间在流处理中是一个重要的概念,而时间语义则用于定义事件发生的时间。Flink 支持三种时间语义,分别是: Processing Time(处理时间): 以机器的系统时间为基准,…...
【大话Presto 】- 核心概念
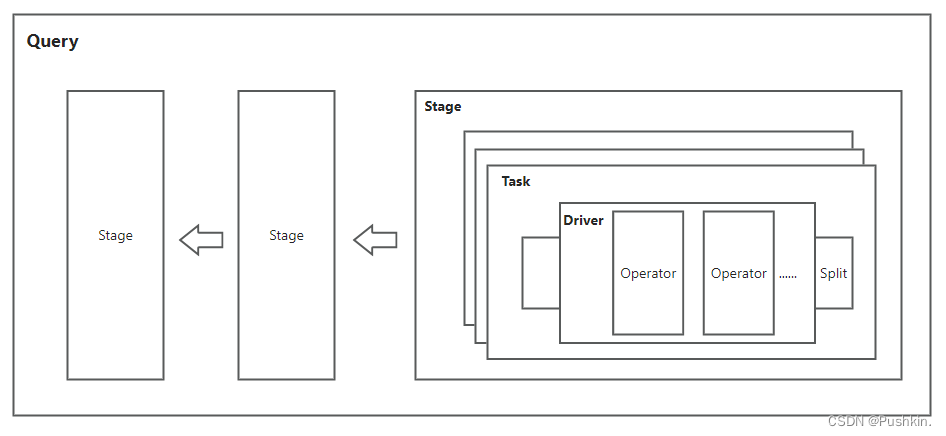
文章目录 前言Operator Model And Iterator Model系统组成Connector数据模型查询执行模型StatementStageTaskSplitDriverOperatorExchangePipeLine 总结 前言 Presto(PrestoDB)是一个FaceBook开源的分布式MPP SQL引擎,旨在处理大规模数据的查…...

阎良区公益创投之“小飞机大梦想” 航模DIY主题活动
创造是人类探索迈出的第一步,科学是开启奇妙世界的金钥匙。为进一步提升“未来星”对科技知识的兴趣,培养他们的科学创新精神,11月16日,阎良区社会组织公益创投——“未来星”助力乡村留守儿童成长计划项目在阎良区聚宝小学开展“…...

springBoot集成websocket实时消息推送
springBoot集成websocket实时消息推送 WebSocket是一种在Web应用程序中实现双向通信的协议。它允许在客户端和服务器之间建立持久性的连接,并支持双向数据传输,实现了实时、低延迟的通信。 📍常见的消息推送方法 WebSocket:通过使…...
web:[BUUCTF 2018]Online Tool
题目 打开页面显示如下,进行代码审计 上述代码主要功能是接收‘host’参数,后使用nmap扫描主机端口 首先检查是否存在HTTP_X_FORWARDED_FOR头,若存在,将值赋值给EMOTE_ADDR,是为了跟踪用户真实的IP地址 后用检查get‘host’是否…...

决策树的Boosting策略是什么
在决策树的Boosting策略中,最常见的算法是梯度提升决策树(Gradient Boosting Decision Trees,简称GBDT)。GBDT是一种集成学习方法,通过串行训练多个决策树,并根据前一个树的预测结果来调整下一个树的训练目…...

SQL Server中substring的用法
SQL Server中substring的用法 SQL中的substring函数是用来截取一个栏位资料中的其中一部分。 例如,我们需要将字符串’abdcsef’中的‘abd’给提取出来,则可用substring 来实现: select substring(abdcsef,1,3)结果为 abd括号中数字’1’表…...
vscode设置latex
vscode配置latex 1.安装vscode,并添加环境变量路径 2.安装latex,bin文件夹添加到环境变量路径 3.vscode安装插件 4.vscode->文件->首选项->显示配置内容->setting.json文件,查看其位置目录,通过我的电脑找到此文件(不要使用v…...

Django模板层
模板之变量 所有的数据类型都可以在模板中使用 render(request, index.html, context{}) render(request, index.html, contextlocals()) """在模板中使用变量的时候,用的是字典的key值,key值value值一般保持一致"""详细…...
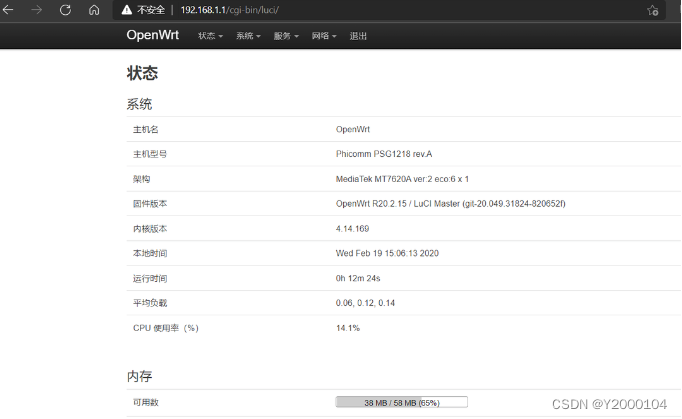
TP_Link WR886N 硬改闪存16M内存64M,刷入openwrt
一、换内存,拆闪存: 1、先原机开机试试是否功能正常; 2、拆机,比较难拆,容易坏外壳; 3、找到内存和闪存,用胶带把边上的小元件,电阻都贴好; 4、加助焊油,用风…...

websocket详解
一、什么是Websocket WebSocket 是一种在单个 TCP 连接上进行 全双工 通信的协议,它可以让客户端和服务器之间进行实时的双向通信。 WebSocket 使用一个长连接,在客户端和服务器之间保持持久的连接,从而可以实时地发送和接收数据。 在 Web…...
可以免费使用的设计素材网站分享
UI设计师最怕什么? 没有创意,没有灵感,没有思路! 在哪里可以得到idea?别担心,往下看! 你知道网络有多大,你想要什么吗?今天,我想和大家分享一些宝藏网页设…...
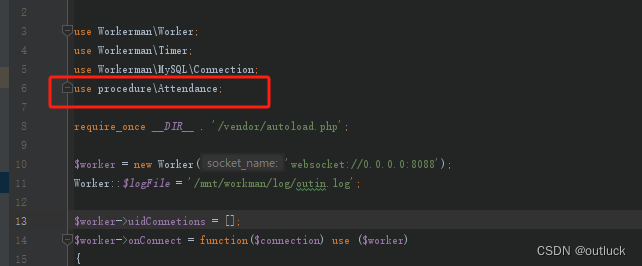
workman使用手册1.0
workman官网地址:高性能PHP应用容器 workerman 1:把workman项目放到linux服务器后,需要启动你的php文件,才可以使用 定位到项目根目录:例:cd /mnt/workman 启动代码:php outin.php start -d 停…...

Cesium深入浅出之自定义材质
引子 做为一名技术宅却没有能拿得出手的技术无疑是最可悲的事情。三年前,当我第一次接触Cesium的时候就被它强大和炫丽所折服,最关键的是它还是开源的。以前我一直是机械地敲着业务代码,好像计算机程序就只能干这点事情一样,而 C…...

Appium移动自动化测试--安装Appium
Appium 自动化测试是很早之前就想学习和研究的技术了,可是一直抽不出一块完整的时间来做这件事儿。现在终于有了。 反观各种互联网的招聘移动测试成了主流,如果再不去学习移动自动化测试技术将会被淘汰。 web自动化测试的路线是这样的:编程语…...

前端学习笔记--ES6
修正 ES6是ECMA为JavaScript制定的第6个标准版本,相关历史可查看此章节《ES6-ECMAScript6简介》。 标准委员会最终决定,标准在每年6月正式发布并作为当年的正式版本,接下来的时间里就在此版本的基础上进行改动,直到下一年6月草案…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
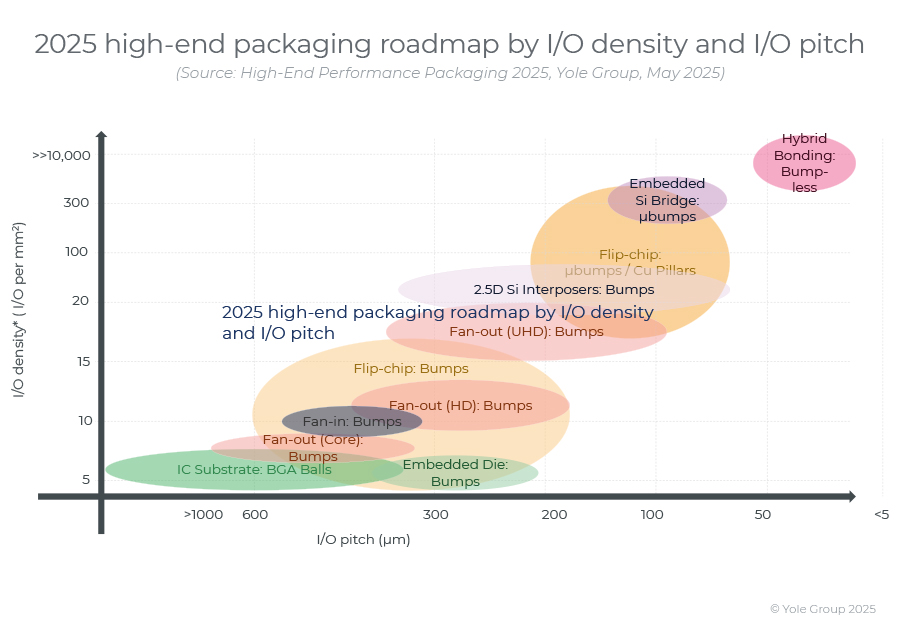
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
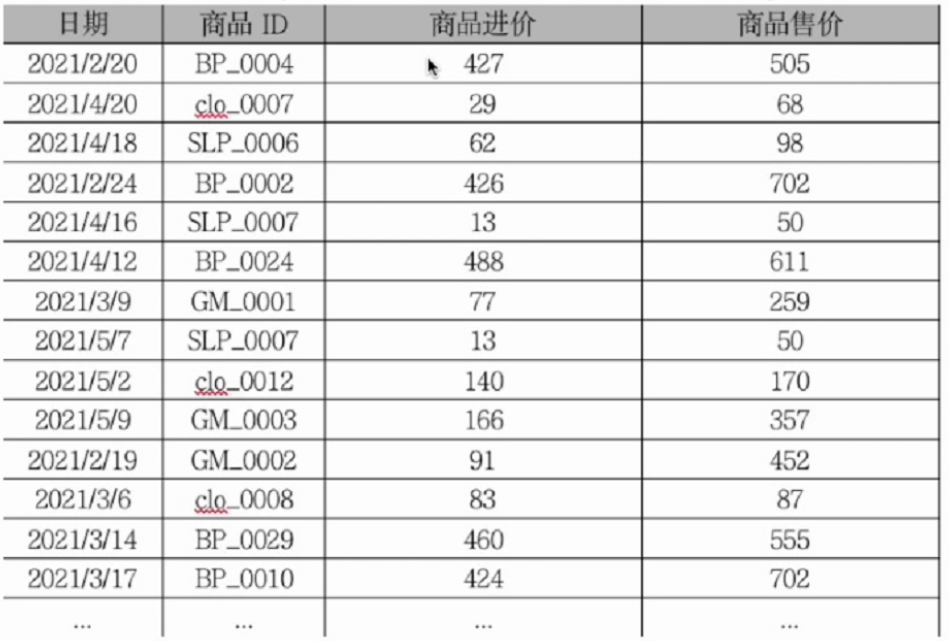
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...
