【matlab学习】现代控制
文章目录
- (1) SISO Modeling
- (2) MIMO Modeling
- (3) 状态空间模型
- (4) 状态空间模型->传递函数
- (5) 传递函数->状态空间模型
- (6) 状态空间模型变换
- (7) 特征值和特征向量
- (8) 广义特征向量
- (9) 状态空间模型->约旦型
(1) SISO Modeling
y ( k + 2 ) + 5 y ( k + 1 ) + 6 y ( k ) = u ( k + 2 ) + 2 u ( k + 1 ) + u ( k ) y(k+2)+5y(k+1)+6y(k)=u(k+2)+2u(k+1)+u(k) y(k+2)+5y(k+1)+6y(k)=u(k+2)+2u(k+1)+u(k)
num_1=[1 2 1];
den_1=[1 5 6];
sys_1=tf(num_1,den_1,-1)
(2) MIMO Modeling
G ( s ) = [ s 2 + 2 s + 1 s 2 + 5 s + 6 s + 5 s + 2 2 s + 3 s 3 + 6 s 2 + 11 s + 6 6 2 s + 7 ] G(s)=\left[\begin{array}{cc}\frac{s^2+2s+1}{s^2+5s+6} & \frac{s+5}{s+2}\\ \frac{2s+3}{s^3+6s^2+11s+6} & \frac{6}{2s+7}\end{array}\right] G(s)=[s2+5s+6s2+2s+1s3+6s2+11s+62s+3s+2s+52s+76]
num={[1 2 1] [1 5]; [2 3] [6]};
den={[1 5 6] [1 2]; [1 6 11 6] [2 7]};
sys_1=tf(num,den)
(3) 状态空间模型
x ˙ = [ 0 1 − 2 − 3 ] x + [ 0 1 ] u y = [ 1 0 ] x \begin{array}{l}\dot{x}=\left[\begin{array}{cc}0&1\\-2&-3\end{array}\right]x+\left[\begin{array}{c}0\\1\end{array}\right]u \\ y=\left[\begin{array}{c}1&0\end{array}\right]x\end{array} x˙=[0−21−3]x+[01]uy=[10]x
A=[0 1; -2 -3];
B=[0; 1]; C=[1 0];
D=0;
sys=ss(A,B,C,D)
(4) 状态空间模型->传递函数
x ˙ = [ 0 1 − 2 − 3 ] x + [ 0 1 ] u y = [ 1 0 ] x \begin{array}{l}\dot{x}=\left[\begin{array}{cc}0&1\\-2&-3\end{array}\right]x+\left[\begin{array}{c}0\\1\end{array}\right]u \\ y=\left[\begin{array}{c}1&0\end{array}\right]x\end{array} x˙=[0−21−3]x+[01]uy=[10]x
sys_tf=tf(sys)
(5) 传递函数->状态空间模型
- 转换函数ss()
sys_1_ss=ss(sys_1)
- 规范形转换函数canon()
sys_can_ss=canon(sys_1,'modal')
- 常微分方程(传递函数)转换为状态空间模型函数dif2ss()
y ′ ′ ′ + 5 y ′ ′ + 8 y ′ + 4 y = 2 u ′ ′ + 14 u ′ + 24 u y^{'''}+5y^{''}+8y^{'}+4y=2u^{''}+14u^{'}+24u y′′′+5y′′+8y′+4y=2u′′+14u′+24u
num_1=[2 14 24]; den_1=[1 5 8 4];
sys_1=tf(num_1,den_1);% 建立传递函数模型
sys_comp=dif2ss(sys_1,'companion')% 求传递函数的友矩阵形状态空间模型
sys_jord=dif2ss(num_1,den_1,'jordan')% 求传递函数的约旦规范形状态空间模型
(6) 状态空间模型变换
{ x ˙ = [ 0 1 0 0 0 1 − 6 − 11 − 6 ] x + [ 0 0 6 ] u y = [ 1 0 0 ] x \left\{\begin{array}{l}\dot{x}=\left[\begin{array}{ccc}0 & 1 & 0\\0 & 0 & 1\\ -6 & -11 & -6\end{array}\right]x+\left[\begin{array}{c}0 \\ 0 \\ 6\end{array}\right]u \\ y=\left[\begin{array}{ccc}1& 0&0\end{array}\right]x\end{array}\right. ⎩ ⎨ ⎧x˙= 00−610−1101−6 x+ 006 uy=[100]x
和
P = [ 1 1 1 − 1 − 2 − 3 1 4 9 ] P=\left[\begin{array}{ccc}1&1&1\\-1&-2&-3\\1&4&9\end{array}\right] P= 1−111−241−39
A=[0 1 0; 0 0 1; -6 -11 -6];
B=[0; 0; 6]; C=[1 0 0]; D=0;
P=[1 1 1; -1 -2 -3; 1 4 9];
sys_in=ss(A,B,C,D);
sys_out=ss2ss(sys_in,inv(P))
(7) 特征值和特征向量
d = eig(A)%只计算所有特征值
[V,D] = eig(A)%同时得到所有特征向量和特征值
(8) 广义特征向量
J = jordan(A)%只计算A矩阵对应的约旦矩阵J
[V,J] = jordan(A)%所有广义特征向量和约旦矩阵J
(9) 状态空间模型->约旦型
x ˙ = [ 0 1 0 0 0 1 − 4 − 8 − 5 ] x + [ 0 0 1 ] u \dot{x}=\left[\begin{array}{ccc}0 & 1&0\\0&0&1\\-4&-8&-5\end{array}\right]x+\left[\begin{array}{c}0\\0\\1\end{array}\right]u x˙= 00−410−801−5 x+ 001 u
y = [ 1 0 0 ] x y=\left[\begin{array}{ccc}1&0&0\end{array}\right]x y=[100]x
A=[0 1 0; 0 0 1; -4 -8 -5];
B=[0; 0; 1]; C=[1 0 0]; D=0;
sys_in=ss(A,B,C,D);
[P,J]=jordan(A);
sys_out=ss2ss(sys_in,inv(P))
相关文章:

【matlab学习】现代控制
文章目录 (1) SISO Modeling(2) MIMO Modeling(3) 状态空间模型(4) 状态空间模型->传递函数(5) 传递函数->状态空间模型(6) 状态空间模型变换(7) 特征值和特征向量(8) 广义特征向量(9) 状态空间模型->约旦型 (1) SISO Modeling y ( k 2 ) 5 y ( k 1 ) 6 y ( k ) …...

Debezium报错处理系列之九十九:ConnectException: Source offset ‘file‘ parameter is missing
Debezium报错处理系列之九十九:ConnectException: Source offset file parameter is missing 一、完整报错二、错误原因三、解决方法研究Debezium技术遇到的各种错误解决方法系列文章传送门: Debezium从入门到精通系列之:百篇系列文章汇总之研究Debezium技术遇到的各种错误的…...

基于深度学习的活体人脸识别检测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1. 活体人脸识别检测算法概述 4.2. 深度学习在活体人脸识别检测中的应用 4.3. 算法流程 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022a 3.部分核心程序 …...
Angular 由一个bug说起之二:trackBy的一点注意事项
trackBy是angualr优化项目性能的一种方法, 通过返回一个具有绑定性的唯一值, 比如id,手机号,身份证号之类的,来让angular能够跟踪数组的项目,根据数据的变化来重新生成DOM, 这样就节约了性能。 但是如果是使用ngFor循环组件&…...
单片机FLASH下载算法的制作
环境 硬件使用正点原子STM32F407探索者V2开发板 编程环境使用MDK 下载工具使用JLINK FLASH芯片使用W25Q128 什么是下载算法 单片机FLASH的下载算法是一个FLM文件,FLM通过编译链接得到,其内部包含一系列对FLASH的操作,包括初始化、擦除、写…...

[nlp] 损失缩放(Loss Scaling)loss sacle
在深度学习中,由于浮点数的精度限制,当模型参数非常大时,会出现数值溢出的问题,这可能会导致模型训练不稳定。为了解决这个问题,损失缩放(Loss Scaling)技术被引入,它通过缩放损失值来解决这个问题。 在深度学习中,损失缩放技术通常是通过将梯度进行缩放来实现的。具…...

Django框架之视图层
【一】三板斧 【1】HttpResponse 返回字符串类型 【2】render 返回html页面,并且在返回给浏览器之前还可以给html页面传值 【3】redirect 重定向页面 在视图文件中写视图函数的时候不能没有返回值了,默认返回的是None,页面上就会报错 d…...
商城免费搭建之java商城 java电子商务Spring Cloud+Spring Boot+mybatis+MQ+VR全景+b2b2c
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...

AI机器学习实战 | 使用 Python 和 scikit-learn 库进行情感分析
专栏集锦,大佬们可以收藏以备不时之需 Spring Cloud实战专栏:https://blog.csdn.net/superdangbo/category_9270827.html Python 实战专栏:https://blog.csdn.net/superdangbo/category_9271194.html Logback 详解专栏:https:/…...
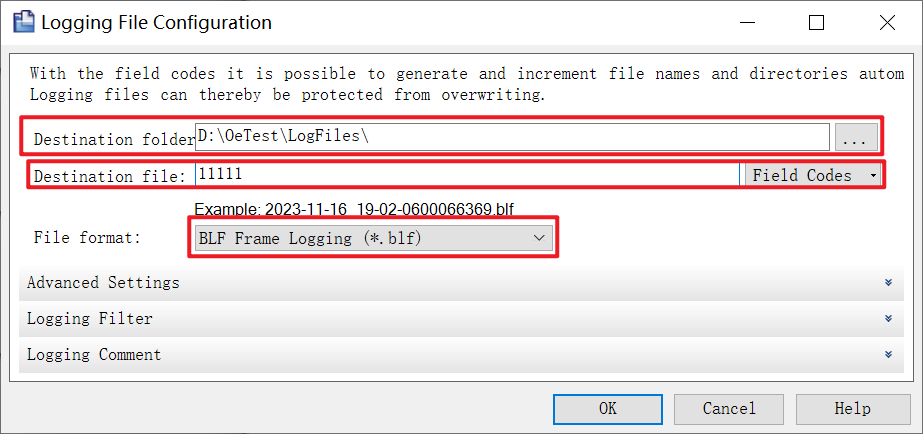
CANoe-Logging模块如何抓取总线数据
在CANoe测量期间(CANoe运行时),总线数据经由Measurement Setup界面的各分析模块的输入口流入Trace、Graphics、Data等窗口中,或统计、或显示、或分析。总线数据除了能流入分析窗口中做解析外,还可以保存到log文件中,留作其他人分析或复现的文件。 在Measurement Setup界…...
Unity中Shader的矩阵加减法
文章目录 前言一、什么是矩阵矩阵就是一组数的阵列 二、矩阵的加法三、矩阵的负值四、矩阵的减法五、矩阵的表示 前言 Unity中Shader用到的矩阵加减法,以及矩阵的一些基础常识 一、什么是矩阵 矩阵就是一组数的阵列 1 2 3 4 5 6 二、矩阵的加法 两个矩阵相加就是…...
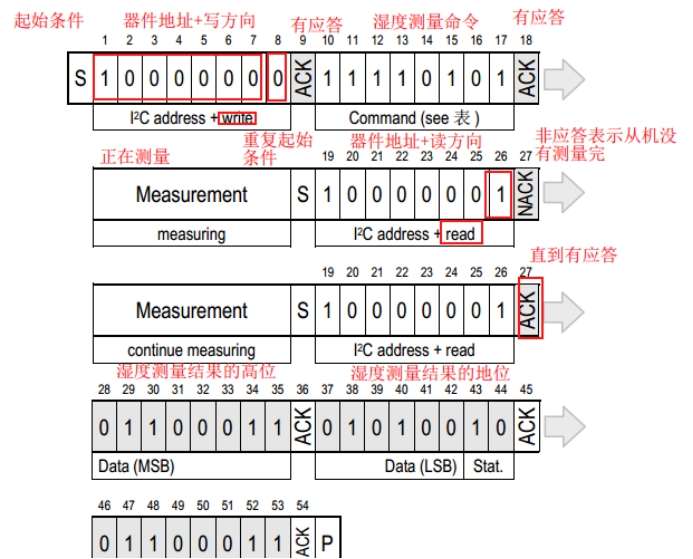
IIC总线概述和通信时序代码详细图文解析
IIC总线 1 IIC总线概述 I2C总线两线制包括:串行数据SDA(Serial Data)、串行时钟SCL(Serial Clock)。总线必须由主机(通常为微控制器)控制,主机产生串行时钟(SCL&#x…...
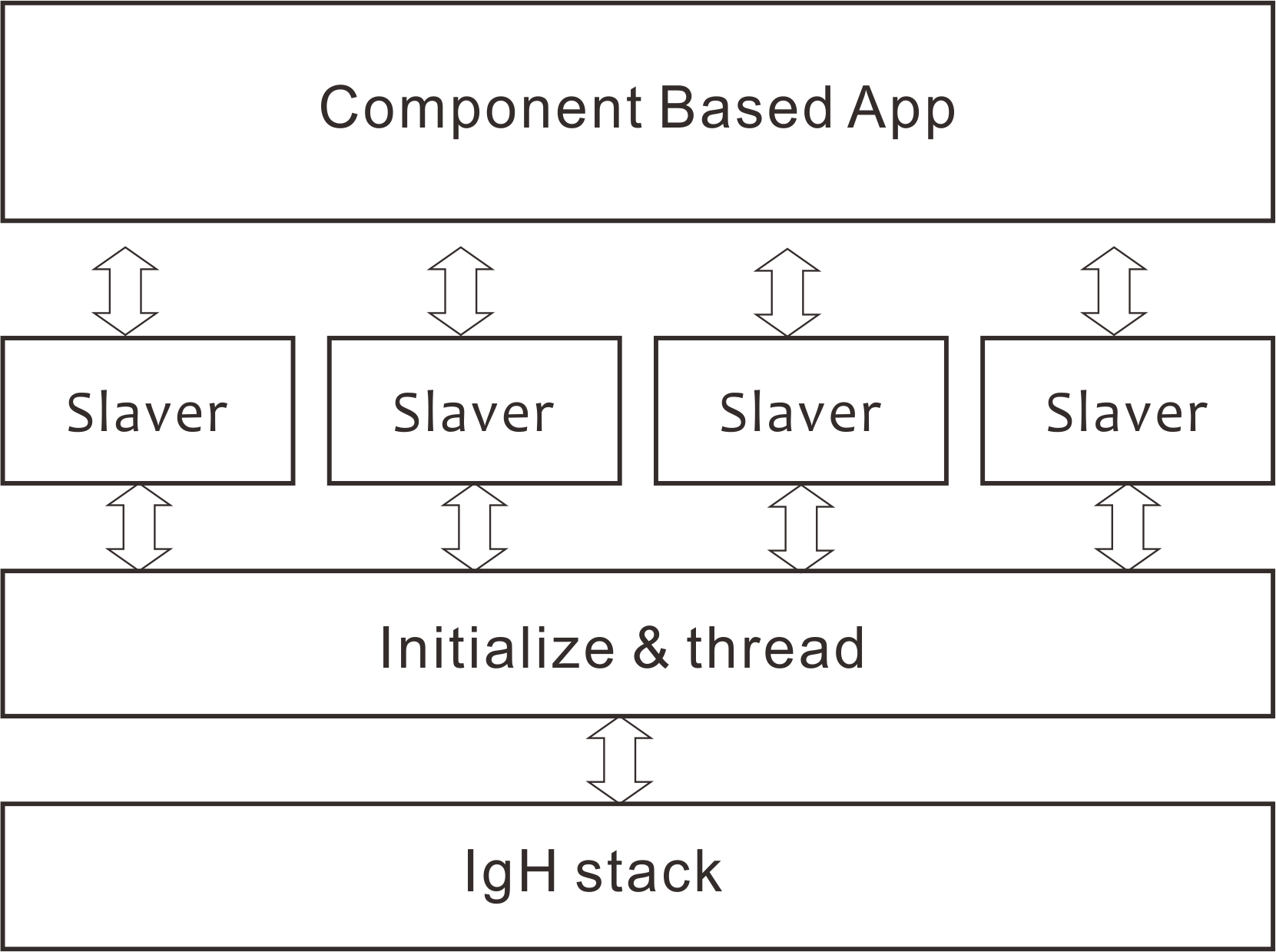
EtherCAT 伺服控制功能块实现
EtherCAT 是运动控制领域主要的通信协议,开源EtherCAT 主站协议栈 IgH 和SOEM 两个项目,IgH 相对更普及一些,但是它是基于Linux 内核的方式,比SOEM更复杂一些。使用IgH 协议栈编写一个应用程序,控制EtherCAT 伺服电机驱…...

如何基于OpenCV和Sklearn算法库开展机器学习算法研究
大家在做机器学习或深度学习研究过程中,不可避免都会涉及到对各种算法的研究使用,目前比较有名的机器学习算法库主要有OpenCV和Scikit-learn(简称Sklearn),二者都支持各种机器学习算法,主要有监督学习、无监…...

在 Node.js 中发出 HTTP 请求的 5 种方法
在 Node.js 中发出 HTTP 请求的 5 种方法 学习如何在 Node.js 中发出 HTTP 请求可能会让人感到不知所措,因为有数十个可用的库,每个解决方案都声称比上一个更高效。一些库提供跨平台支持,而另一些库则关注捆绑包大小或开发人员体验。 在这篇…...
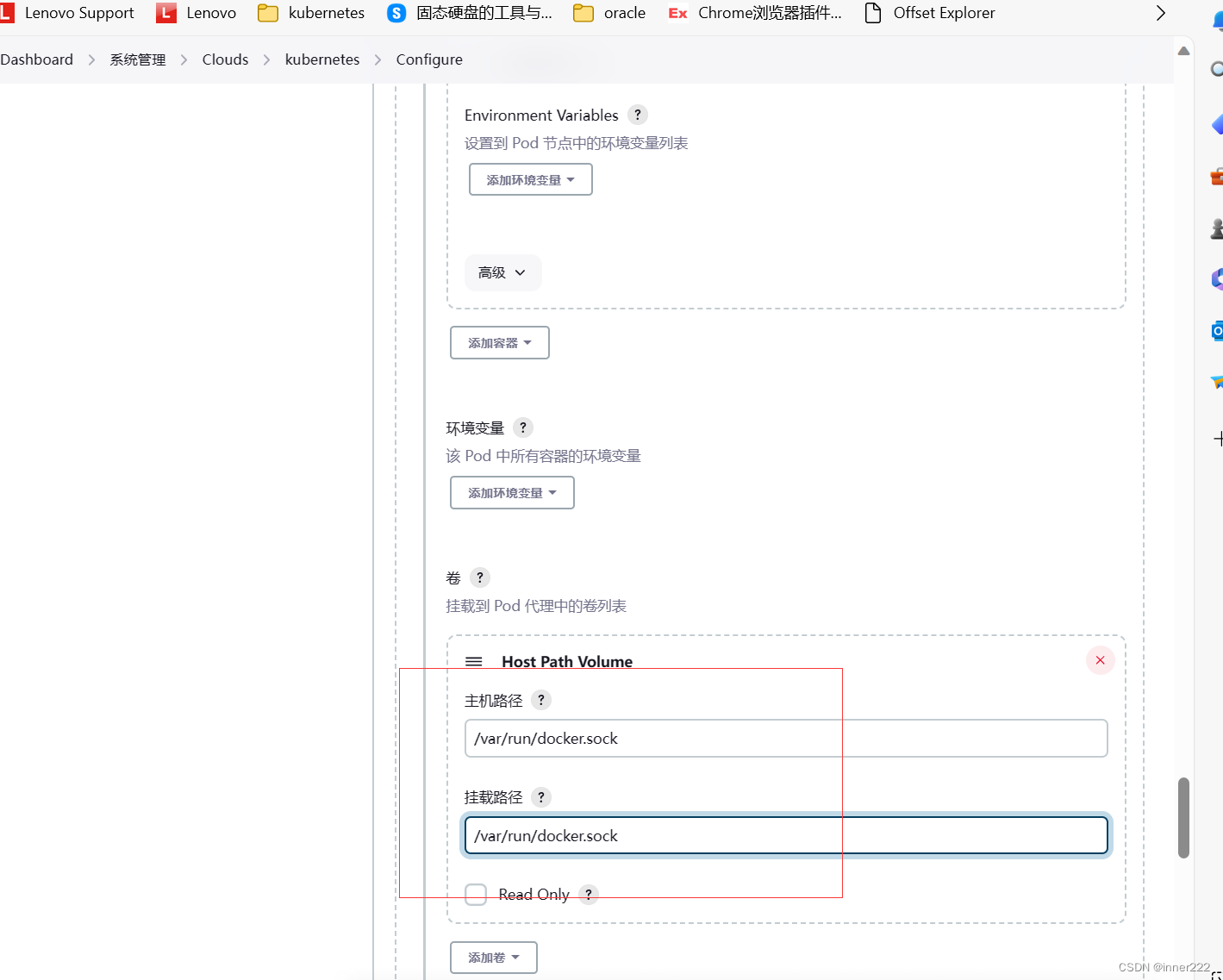
pipeline agent分布式构建
开启 agent rootjenkins:~/learning-jenkins-cicd/07-jenkins-agents# docker-compose -f docker-compose-inbound-agent.yml up -d Jenkins配置添加 pipeline { agent { label docker-jnlp-agent }parameters {booleanParam(name:pushImage, defaultValue: true, descript…...

MySQL(17):触发器
概述 MySQL从 5.0.2 版本开始支持触发器。MySQL的触发器和存储过程一样,都是嵌入到MySQL服务器的一段程序。 触发器是由 事件来触发 某个操作,这些事件包括 INSERT 、 UPDATE 、 DELETE 事件。 所谓事件就是指用户的动作或者触发某项行为。 如果定义了触…...
挖掘PostgreSQL事务的“中间态”----更加严谨的数据一致性?
1.问题 今天在上班途中,中心的妹纸突然找我,非常温柔的找我帮忙看个数据库的报错。当然以我的性格,妹子找我的事情对我来说优先级肯定是最高的,所以立马放下手中的“小事”,转身向妹子走去。具体是一个什么样的问题呢…...

多种方法实现conda环境迁移
Conda 为包管理器和虚拟环境管理器。在配置完项目环境,进行了编写和测试代码,需要大量数据测试运行时,需要将其移至另一台主机上。Conda 提供了多种保存和移动环境的方法。 方法1: scp拷贝法,直接将envs的环境文件夹…...
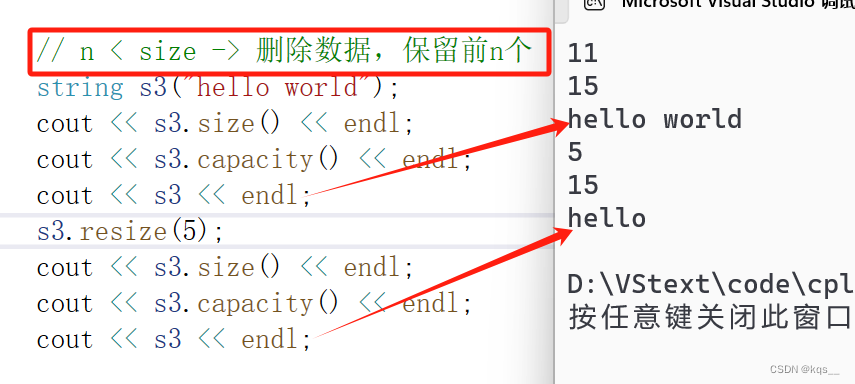
C++ string类(一)
1.C语言中的字符串 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数,但是这些库函数与字符串是分离开的,不太符 OOP(Object Oriented Programming)的思想,而且…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
