【机器学习】线性回归算法:原理、公式推导、损失函数、似然函数、梯度下降
1. 概念简述
线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析,其特点为一个或多个称为回归系数的模型参数的线性组合。如下图所示,样本点为历史数据,回归曲线要能最贴切的模拟样本点的趋势,将误差降到最小。
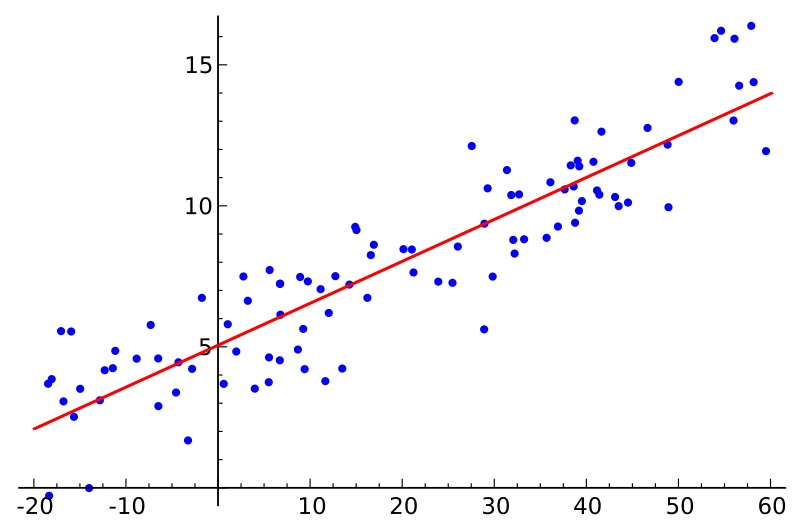
2. 线性回归方程
线形回归方程,就是有 n 个特征,然后每个特征 Xi 都有相应的系数 Wi ,并且在所有特征值为0的情况下,目标值有一个默认值 W0 ,因此:
线性回归方程为:
整合后的公式为:
3. 损失函数
损失函数是一个贯穿整个机器学习的一个重要概念,大部分机器学习算法都有误差,我们需要通过显性的公式来描述这个误差,并将这个误差优化到最小值。假设现在真实的值为 y,预测的值为 h 。
损失函数公式为:
也就是所有误差和的平方。损失函数值越小,说明误差越小,这个损失函数也称最小二乘法。
4. 损失函数推导过程
4.1 公式转换
首先我们有一个线性回归方程:
为了方便计算计算,我们将线性回归方程转换成两个矩阵相乘的形式,将原式的 后面乘一个
此时的 x0=1,因此将线性回归方程转变成 ,其中
和
可以写成矩阵:
4.2 误差公式
以上求得的只是一个预测的值,而不是真实的值,他们之间肯定会存在误差,因此会有以下公式:
我们需要找出真实值 与预测值
之间的最小误差
,使预测值和真实值的差距最小。将这个公式转换成寻找不同的
使误差达到最小。
4.3 转化为  求解
求解
由于 既存在正数也存在负数,所以可以简单的把这个数据集,看作是一个服从均值
,方差为
的正态分布。
所以  出现的概率满足概率密度函数:
出现的概率满足概率密度函数:
把 代入到以上的高斯分布函数(即正态分布)中,变成以下式子:
到此,我们将对误差 的求解转换成对
的求解了。
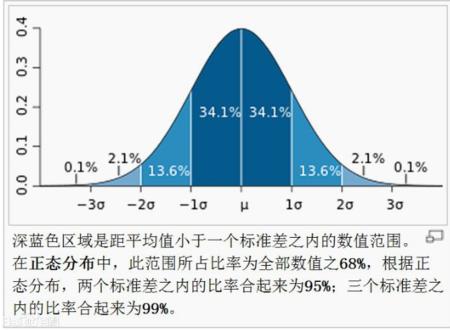
在求解这个公式时,我们要得到的是误差 最小,也就是求概率
最大的。因为误差
满足正态分布,因此在正太曲线中央高峰部的概率
是最大的,此时标准差
为0,误差是最小的。
尽管在生活中标准差肯定是不为0的,没关系,我们只需要去找到误差值出现的概率最大的点。现在,问题就变成了怎么去找误差出现概率最大的点,只要找到,那我们就能求出
4.4 似然函数求 
似然函数的主要作用是,在已经知道变量 x 的情况下,调整 ,使概率 y 的值最大。
似然函数理解:
以抛硬币为例,正常情况硬币出现正反面的概率都是0.5,假设你在不确定这枚硬币的材质、重量分布的情况下,需要判断其是否真的是均匀分布。在这里我们假设这枚硬币有 的概率会正面朝上,有
的概率会反面朝上。
为了获得 的值,将硬币抛10次,H为正面,T为反面,得到一个正反序列 x = HHTTHTHHHH,此次实验满足二项分布,这个序列出现的概率为
,我们根据一次简单的二项分布实验,得到了一个关于
的函数,这实际上是一个似然函数,根据不同的
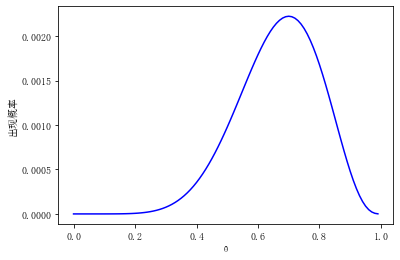
值绘制一条曲线,曲线就是
的似然函数,y轴是这一现象出现的概率。
从图中可见,当 等于 0.7 时,该序列出现的概率是最大的,因此我们确定该硬币正面朝上的概率是0.7。
因此,回到正题,我们要求的是误差出现概率 的最大值,那就做很多次实验,对误差出现概率累乘,得出似然函数,带入不同的
,看
是多少时,出现的概率是最大的,即可确定
的值。
综上,我们得出求  的似然函数为:
的似然函数为:
4.5 对数似然
由于上述的累乘的方法不太方便我们去求解 ,我们可以转换成对数似然,将以上公式放到对数中,然后就可以转换成一个加法运算。取对数以后会改变结果值,但不会改变结果的大小顺序。我们只关心
等于什么的时候,似然函数有最大值,不用管最大值是多少,即,不是求极值而是求极值点。注:此处log的底数为e。
对数似然公式如下:
对以上公式化简得:
4.6 损失函数
我们需要把上面那个式子求得最大值,然后再获取最大值时的 值。 而上式中
是一个常数项,所以我们只需要把减号后面那个式子变得最小就可以了,而减号后面那个部分,可以把常数项
去掉,因此我们得到最终的损失函数如下,现在只需要求损失函数的最小值。
注:保留 是为了后期求偏导数。
损失函数越小,说明预测值越接近真实值,这个损失函数也叫最小二乘法。
5. 梯度下降
损失函数中 xi 和 yi 都是给定的值,能调整的只有 ,如果随机的调整,数据量很大,会花费很长时间,每次调整都不清楚我调整的是高了还是低了。我们需要根据指定的路径去调节,每次调节一个,范围就减少一点,有目标有计划去调节。梯度下降相当于是去找到一条路径,让我们去调整
。
梯度下降的通俗理解就是,把对以上损失函数最小值的求解,比喻成梯子,然后不断地下降,直到找到最低的值。
5.1 批量梯度下降(BGD)
批量梯度下降,是在每次求解过程中,把所有数据都进行考察,因此损失函数因该要在原来的损失函数的基础之上加上一个m:数据量,来求平均值:
因为现在针对所有的数据做了一次损失函数的求解,比如我现在对100万条数据都做了损失函数的求解,数据量结果太大,除以数据量100万,求损失函数的平均值。
然后,我们需要去求一个点的方向,也就是去求它的斜率。对这个点求导数,就是它的斜率,因此我们只需要求出 的导数,就知道它要往哪个方向下降了。它的方向先对所有分支方向求导再找出它们的合方向。
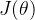 的导数为:
的导数为:
由于导数的方向是上升的,现在我们需要梯度下降,因此在上式前面加一个负号,就得到了下降方向,而下降是在当前点的基础上下降的。
批量梯度下降法下降后的点为:
新点是在原点的基础上往下走一点点,斜率表示梯度下降的方向, 表示要下降多少。由于不同点的斜率是不一样的,以此循环,找到最低点。
批量梯度下降的特点:每次向下走一点点都需要将所有的点拿来运算,如果数据量大非常耗时间。
5.2 随机梯度下降(SGD)
随机梯度下降是通过每个样本来迭代更新一次。对比批量梯度下降,迭代一次需要用到所有的样本,一次迭代不可能最优,如果迭代10次就需要遍历整个样本10次。SGD每次取一个点来计算下降方向。但是,随机梯度下降的噪音比批量梯度下降要多,使得随机梯度下降并不是每次迭代都向着整体最优化方向。
随机梯度下降法下降后的点为:
每次随机一个点计算,不需要把所有点拿来求平均值,梯度下降路径弯弯曲曲趋势不太好。
5.3 mini-batch 小批量梯度下降(MBGO)
我们从上面两个梯度下降方法中可以看出,他们各自有优缺点。小批量梯度下降法在这两种方法中取得了一个折衷,算法的训练过程比较快,而且也要保证最终参数训练的准确率。
假设现在有10万条数据,MBGO一次性拿几百几千条数据来计算,能保证大体方向上还是下降的。
小批量梯度下降法下降后的点为:
用来表示学习速率,即每次下降多少。已经求出斜率了,但是往下走多少合适呢,
值需要去调节,太大的话下降方向会偏离整体方向,太小会导致学习效率很慢。
相关文章:
【机器学习】线性回归算法:原理、公式推导、损失函数、似然函数、梯度下降
1. 概念简述 线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析,其特点为一个或多个称为回归系数的模型参数的线性组合。如下图所示,样本点为历史数据,回归曲线要能最贴切的模拟样本点的趋势,将误差降到最小。 2. 线…...

Word中NoteExpress不显示的问题
首先确认我们以及安装了word插件 我们打开word却没有。此时我们打开:文件->选项->加载项 我们发现被禁用了 选择【禁用项目】(如果没有,试一试【缓慢且禁用的加载项】),点击转到 选择启用 如果没有禁用且没有出…...

连接池的大体介绍,常用配置及在springboot项目中的应用
连接池 在Java开发中,常见的数据库连接池有哪些?_java常见数据库连接池_举个例子学java的博客-CSDN博客 常见的连接池配置参数 java 连接池参数 - 百度文库 连接池的具体配法 Spring Boot之默认连接池配置策略_spring mysql默认连接池大小-CSDN博客...
Java之SpringCloud Alibaba【九】【Spring Cloud微服务Skywalking】
Java之SpringCloud Alibaba【一】【Nacos一篇文章精通系列】跳转Java之SpringCloud Alibaba【二】【微服务调用组件Feign】跳转Java之SpringCloud Alibaba【三】【微服务Nacos-config配置中心】跳转Java之SpringCloud Alibaba【四】【微服务 Sentinel服务熔断】跳转Java之Sprin…...
wpf devexpress设置行和编辑器
如下教程示范如何计算行布局,特定的表格单元编辑器,和格式化显示值。这个教程基于前一个文章 选择行显示 GridControl为所有字段生成行和绑定数据源,如果AutoGenerateColumns 属性选择AddNew。添加行到GridControl精确显示为特别的几行设置。…...
AdaBoost 算法:理解、实现和掌握 AdaBoost
一、介绍 Boosting 是一种集成建模技术,由 Freund 和 Schapire 于 1997 年首次提出。从那时起,Boosting 就成为解决二元分类问题的流行技术。这些算法通过将大量弱学习器转换为强学习器来提高预测能力 。 Boosting 算法背后的原理是,我们首先…...
基于ssm+vue设备配件检修管理系统
摘要 随着工业设备的日益复杂和多样化,设备配件的检修管理成为保障生产运行和设备寿命的关键环节。本研究基于SSM框架(Spring Spring MVC MyBatis),致力于设计和实现一套全面、高效的设备配件检修管理系统。该系统不仅能够提高设…...
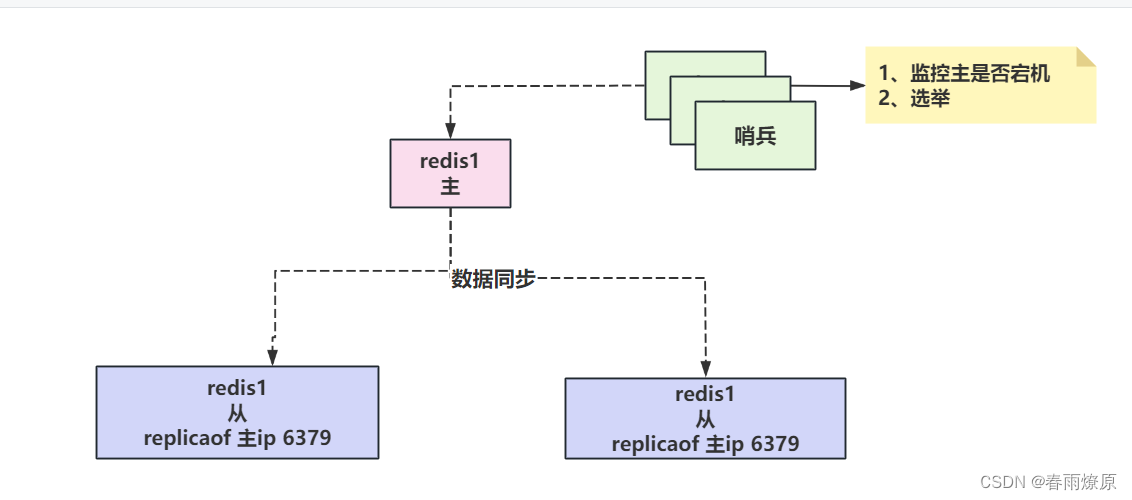
Reids集群
目录 一、集群的概念 1.为什么要搭建集群? 2.Redis搭建集群是否需要考虑状态同步的问题? 二、Redis集群的模式 1.redis集群--主从模式 1.1什么是Redis的主从模式? 1.2.主从模式它们之间的数据是怎么实现一个同步的? 1.3.主…...

自定义指令基础
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives) 选项式API_自定义指令 <template><h3>自定义指令</h3><p v-author>文本信息</p> </template> <script> e…...
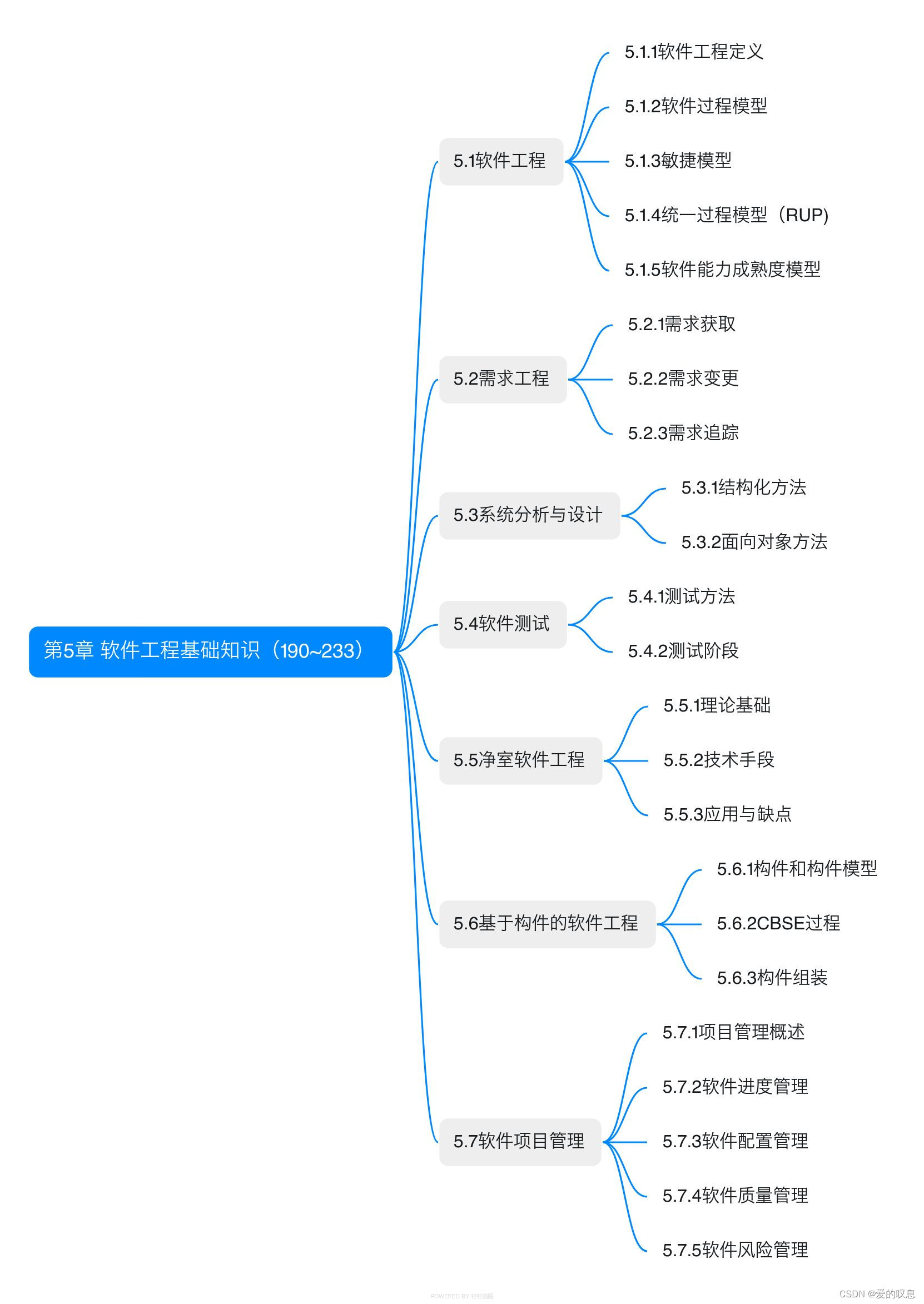
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】 课本里章节里所有蓝色字体的思维导图...
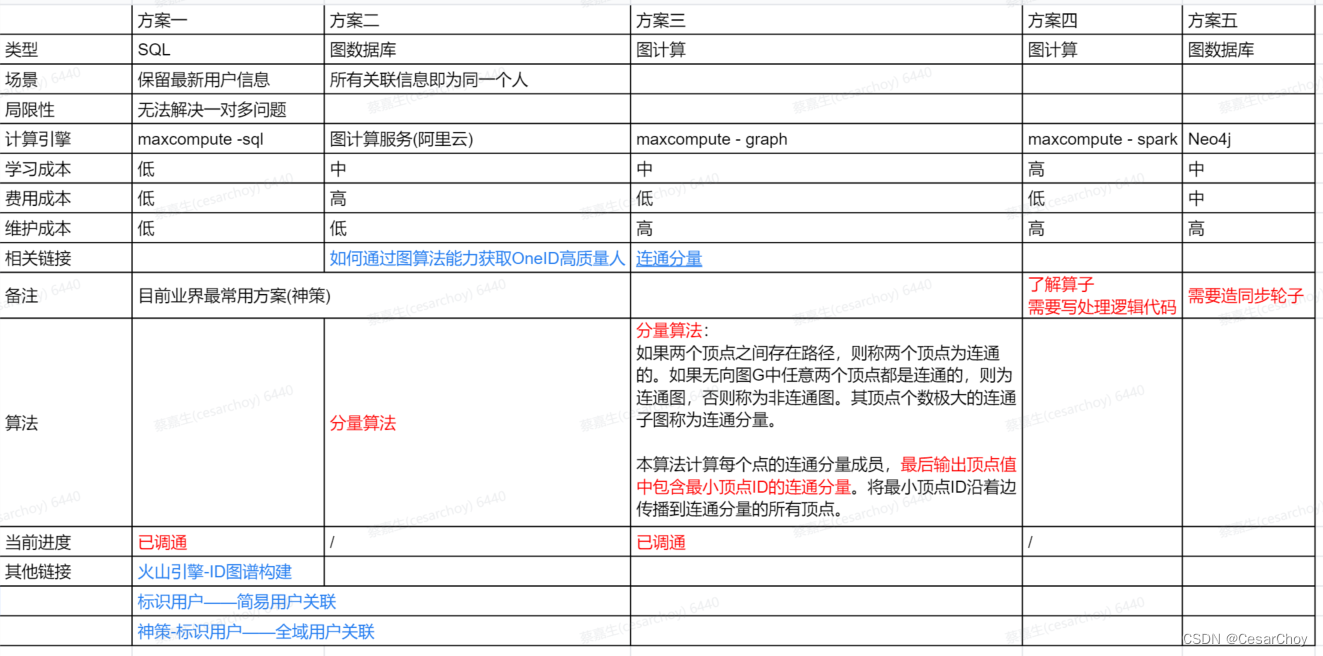
Oneid方案
一、前文 用户画像的前提是标识出用户,存在以下场景:不同业务系统对同一个人的标识,匿名用户行为的行为归因;本文提供多种解决方案,提供大家思考。 二、方案矩阵 三、其他 相关连接: 如何通过图算法能力获…...
【超好用的工具库】hutool-all工具库的基本使用
简介(可不看): hutool-all是一个Java工具库,提供了许多实用的工具类和方法,用于简化Java开发过程中的常见任务。它包含了各种模块,涵盖了字符串操作、日期时间处理、加密解密、文件操作、网络通信、图片处…...

趣学python编程 (一、计算机基础知识科普)
未来是高度科技化和智能化的时代。过去不识字的叫“文盲”,如今不懂点计算机知识,则可能是新时代的“文盲”。不论从事什么行业,了解下计算机和编程都是有益的。Python 连续多年占据最受欢迎的编程语言榜首,未来Python有机会成为像…...
亚马逊云科技云存储服务指南
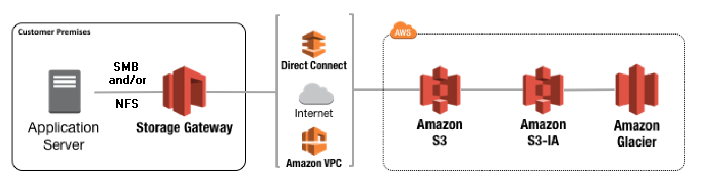
文章作者:Libai 高效的云存储服务对于现代软件开发中的数据管理至关重要。亚马逊云科技云存储服务提供了强大的工具,可以简化工作流程并增强数据管理能力。 亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例、技术专栏…...
随机链表的复制
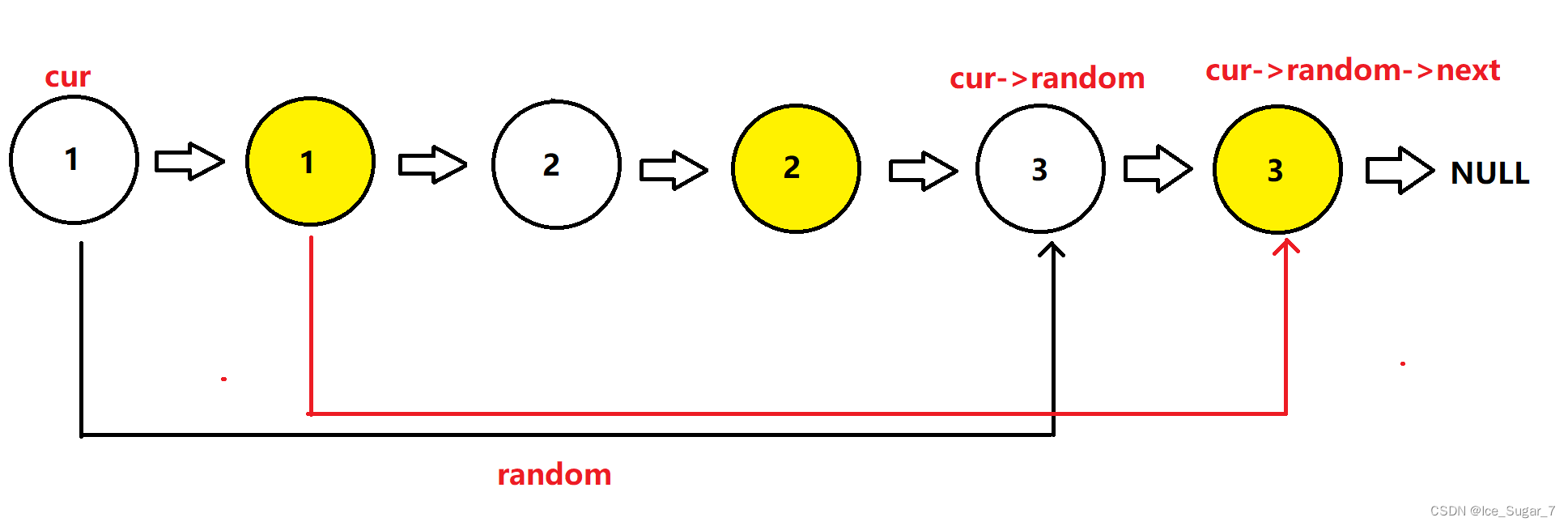
文章目录 🍉前言🍉题目🍉分析🍉思路一:暴力解法🍉思路二:很绝的办法 🍉前言 果然,力扣的简单题不一定简单,但是中等和较难的题一定很麻烦。 这道题相当综合&…...

树莓派4b编译FFmpeg支持硬件编解码
ffmpeg h264_omx解码器充分发挥树莓派gpu性能 准备 树莓派4b ,64位系统 修改树莓派的启动设置文件(/boot/config.txt)进行如下的调整: gpu_mem=256 framebuffer_depth=16安装依赖 常规依赖: sudo apt update sudo apt upgrade sudo apt -y install autoconf automake …...

开启CentOS/Debian自带的TCP BBR加速
BBR 是什么我就不多做介绍了。如果系统自带内核高于4.9 则默认已包含 BBR。 操作方法: 1、使用 root 权限运行下面代码 uname -r //内核版本高于 4.9 就行。2、开启BBR echo "net.core.default_qdiscfq" >> /etc/sysctl.conf echo "net.ip…...
视频推拉流EasyDSS直播点播平台获取指定时间快照的实现方法
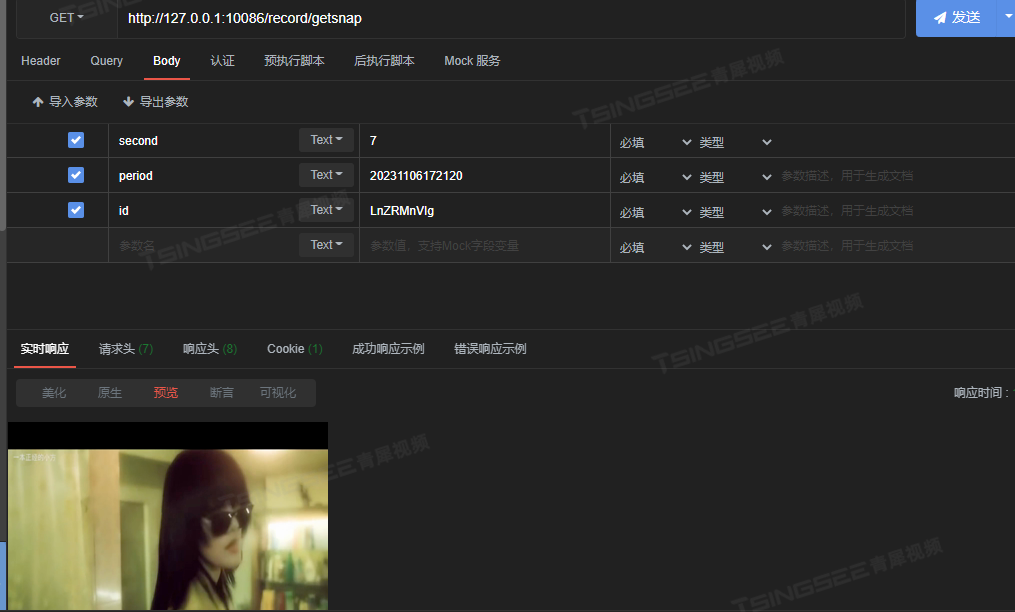
视频推拉流直播点播系统EasyDSS平台,可提供流畅的视频直播、点播、视频推拉流、转码、管理、分发、录像、检索、时移回看等功能,可兼容多操作系统,在直播点播领域具有广泛的场景应用。为了便于用户集成、调用与二次开发。 今天我们来介绍下在…...

CSS---关于font文本属性设置样式总结
目录 1、color属性 2、font-size属性 3、font-weight属性 4、font-family属性 5、text-align属性 6、line-height属性 7、text-indent属性 8、letter-spacing属性 9、word-spacing属性 10、word-break属性 11、white-space属性 12、text-transform 12、writing-mo…...

7、使用真机调试鸿蒙项目
此处以华为手机为例,版本为鸿蒙4.0. 一、打开手机调试功能 1、打开开发者模式 打开“设置”—“关于手机”,连续点击“软件版本”可打开开发者模式 2、开启USB调试功能 打开“设置”—“系统更新”—“开发者选项”,下拉找到“USB调试”…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
