uniapp实现下载图片到本地
uniapp实现下载图片到本地
在uniapp开发中,可以使用uni.downloadFile方法实现下载文件功能,客户端直接发起一个 HTTP GET 请求,返回文件的本地临时路径。
const urlPath = 'http://192.168.0.1:8080/fileApi/logo.png'
uni.downloadFile({url: urlPath,success(res){// 这时会产生一个临时路径,在应用本次启动期间可以正常使用。if (res.statusCode == 200) {// 需要将图片保存到相册uni.saveImageToPhotosAlbum({filePath: res.tempFilePath, // 图片文件路径,可以是临时文件路径也可以是永久文件路径,不支持网络图片路径success(res){uni.showToast({title: '保存成功',icon: 'none'})// 如果保存成功需要打开查看,请使用以下方法,同时也支持打开文件uni.openDocument({filePath: res.savedFilePath,success(res){},fail(err){uni.showToast({title: '手机不支持该文件类型,请安装wps或office应用',icon: 'none'})}})},fail(err){uni.showToast({title: '图片保存失败',icon: 'none'})}})} else {uni.showToast({title: '下载失败,请稍后再试',icon: 'none'})}},fail(err) {uni.showToast({title: '下载失败,请稍后再试',icon: 'none'})}
})
相关文章:

uniapp实现下载图片到本地
uniapp实现下载图片到本地 在uniapp开发中,可以使用uni.downloadFile方法实现下载文件功能,客户端直接发起一个 HTTP GET 请求,返回文件的本地临时路径。 const urlPath http://192.168.0.1:8080/fileApi/logo.png uni.downloadFile({url:…...
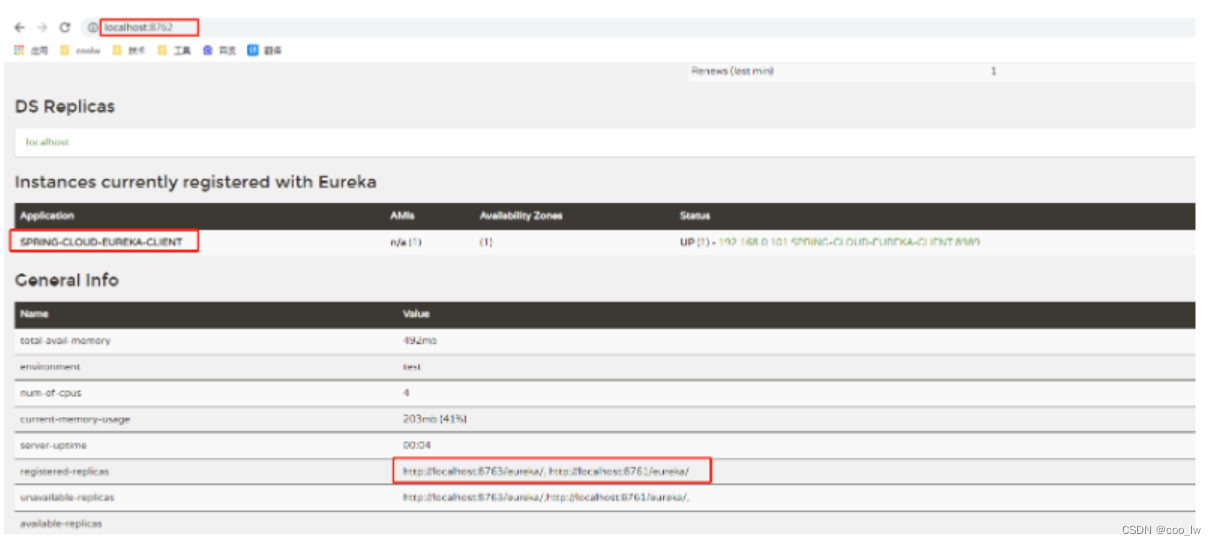
spring cloud-注册中心(Eureka)
一、服务注册中心组件(*) 定义:服务注册中心就是在整个微服务架构单独抽取一个服务,该服务不做项目中任何业务功能,仅用来在微服务中记录微服务、对微服务进行健康状态检查,及服务元数据信息存储常用的注册中心:eurek…...

004 OpenCV akaze特征点检测匹配
目录 一、环境 二、akaze特征点算法 2.1、基本原理 2.2、实现过程 2.3、实际应用 2.4、优点与不足 三、代码 3.1、数据准备 3.2、完整代码 一、环境 本文使用环境为: Windows10Python 3.9.17opencv-python 4.8.0.74 二、akaze特征点算法 特征点检测算法…...
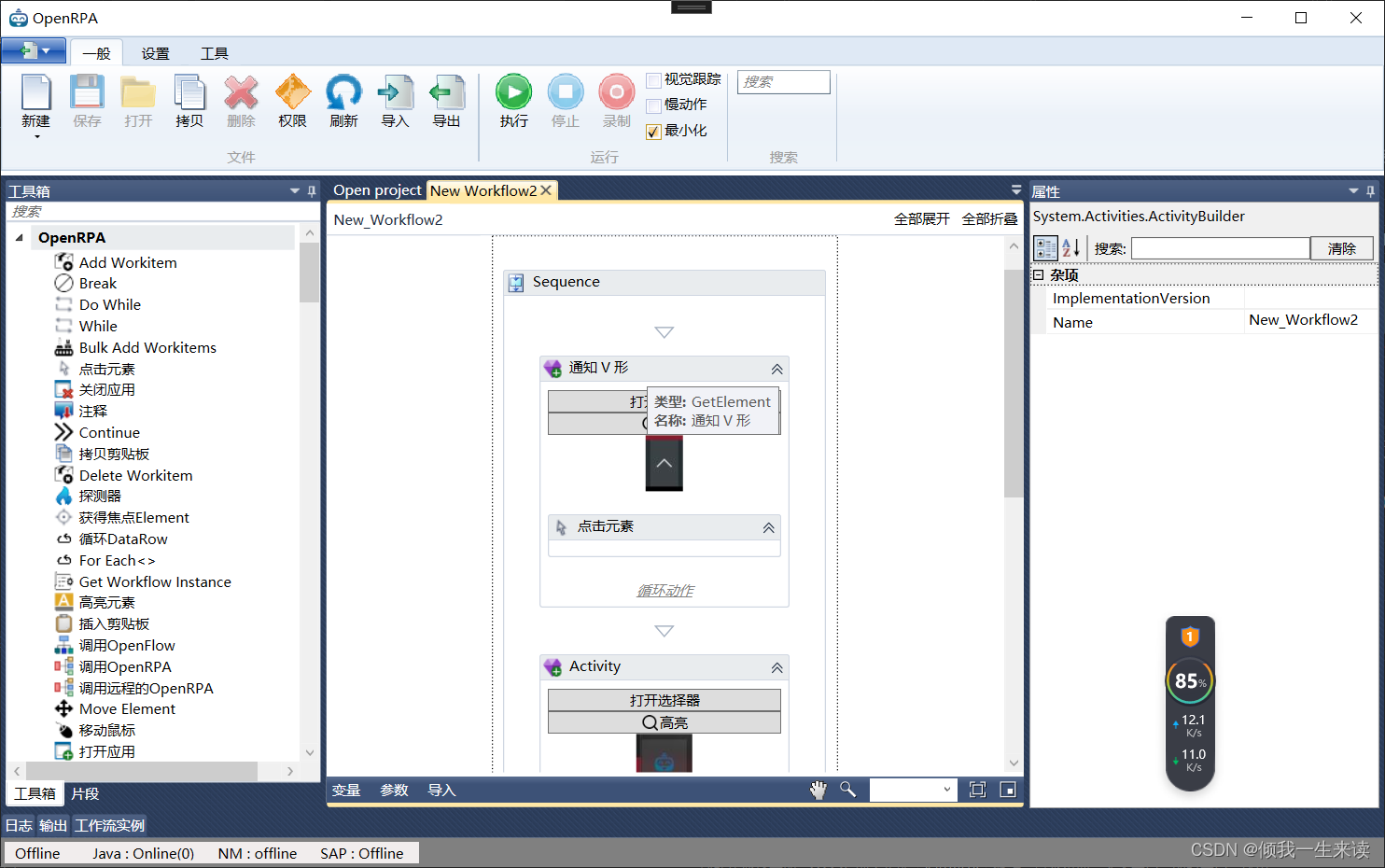
openRPA开源项目源码编译
最近接触到了一个新的领域——RPA,RPA全称Robotic Process Automation,中文名为机器人流程自动化。RPA可以视作一个数字机器人,它可以通过程序来模拟人与软件系统的交互过程,代替人工将大量重复、有规则的计算机操作自动化&#x…...
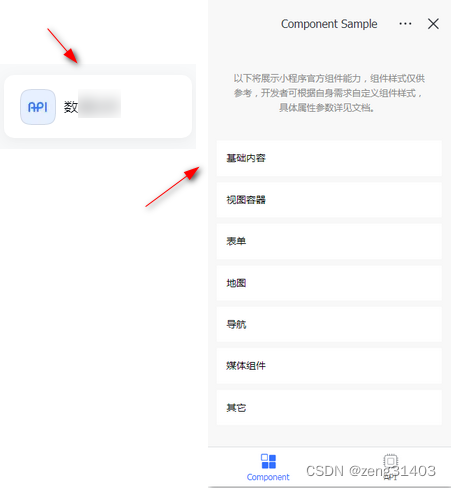
飞书开发学习笔记(八)-开发飞书小程序Demo
飞书开发学习笔记(八)-开发飞书小程序Demo 一.小程序开发概述 1.1 小程序开发概述 飞书开发文档中查看:小程序开发概述 飞书小程序是指可以运行在飞书客户端中的小程序,小程序的一套代码可以适配 Android、iOS、PC 多平台,且用户体验与飞书…...

Unity UI 完全解决方案
Unity UI 完全解决方案 在我学习开发 unity 游戏尝试进行 UI 的构建的过程中,尝试寻找当前 Unity 最为推荐的 UI 构建方式,或者说最优的框架方案。 在中文网里寻找了半天,总感觉很多文章和教程给了方案,但又说不清楚为啥用这个方…...

为什么打开idea时,没有启动页面,如何解决?
更新idea2021.2后,当双击idea打开时,发现没有启动界面,直接进入IDEA界面,中间等待时间,让人误以为没有打开idea成功,使得多次点击idea图标。 解决方案就是 在idea界面菜单栏中找到帮助(Help)&a…...

golang - 嵌入静态文件打包
go-bindata - embed结合嵌入静态文件打包可执行二进制文件 ## embed 嵌入静态文件到可执行二进制文件 # 安装go-bindata go get -u github.com/jteeuwen/go-bindata/... # 打包静态文件 go-bindata web/... 执行次命令之后会在项目目录下生成bindata.go文件,示例命令中模板文…...
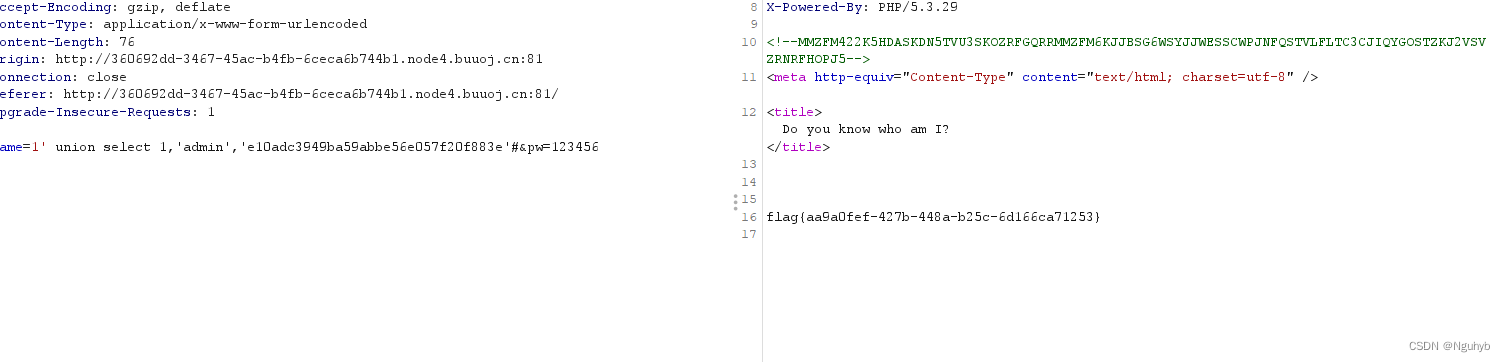
SQL题
[极客大挑战 2019]EasySQL 进行简单的尝试,就知道是单引号的字符型注入 万能密码进行一个简单的尝试 结果就出来了 还是要了解一下原理 输入的是1,形成的sql语句是错误的SELECT*FROM table_name WHERE username1and password123; 第一个单引号和第二个…...

GUN介绍
介绍 GNU(GNU’s Not Unix)是一个自由操作系统项目,名字是一个递归的 GNU’s Not Unix 缩写,其目标是创建一个类Unix的操作系统。 该项目由Richard Stallman于1983年发起,并由自由软件基金会(Free Softwa…...

《Effective C++》条款15
在资源管理类中提供对原始资源的访问 class A {... }; int day(const A* ptr) {... } int main() {shared_ptr<A> ptr(new A);cout << day(ptr) << endl; } 这样写是错误的。因为day函数要求的参数是指针,而你传的实际上是一个对象。 如何解决呢&…...
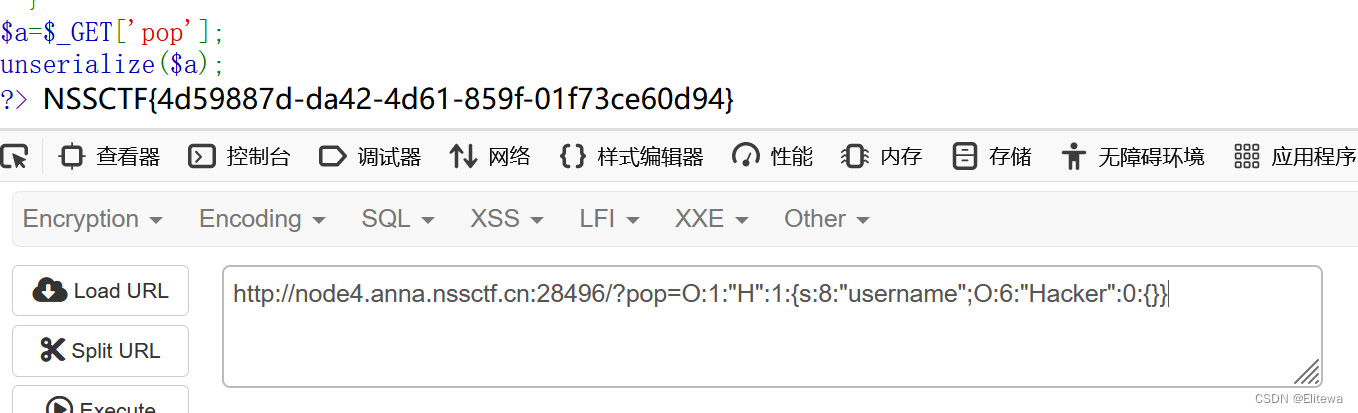
CTFd-Web题目动态flag
CTFd-Web题目动态flag 1. dockerhub注册2. dockerfile编写3. 上传到docker仓库4. 靶场配置5. 动态flag实现 1. dockerhub注册 想要把我们的web题目容器上传到docker仓库中,我们需要dockerhub官网注册一个账号,网址如下 https://hub.docker.com/2. dock…...
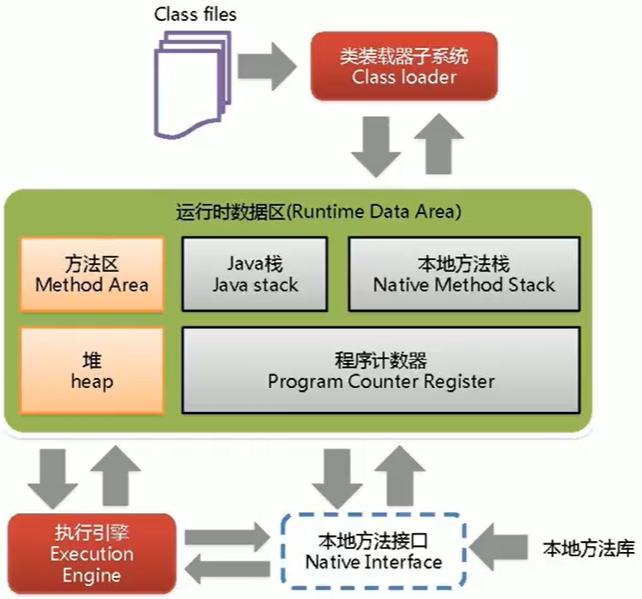
系列九、对象的生命周期和GC
一、堆细分 Java堆从GC的角度还可以细分为:新生代(eden【伊甸园区】、from【幸存者0区】、to【幸存者1区】)和老年代。 二、MinorGC的过程 复制>清空》交换 1、eden、from区中的对象复制到to区,年龄1 首先,当eden区…...

spark 窗口滑动用于在不同的数据块之间执行操作
在 Scala 中进行分布式执行,例如使用 Apache Spark,可以通过设置窗口滑动来实现不同 RDD 之间的关联处理。窗口滑动是一种窗口操作,用于在不同的数据块之间执行操作。 以下是一个简单的示例,演示如何在 Spark 中使用窗口滑动&…...
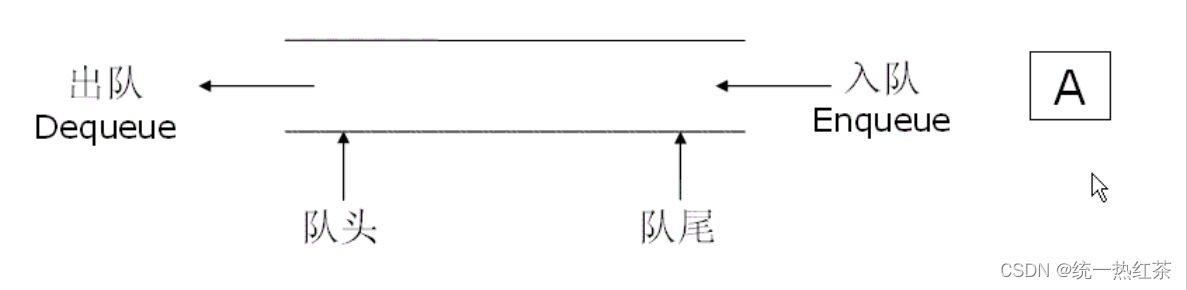
【数据结构】栈与队列的实现
栈与队列是数据结构中重要的结构, 可以用于解决一些题目 模拟实现时可以增加对于这些结构的理解,也可以巩固我们的语言水平,解决某些题目也会有很好的效果 话不多说 目录 栈的实现结构体的定义:初始化栈:压栈:出栈&am…...
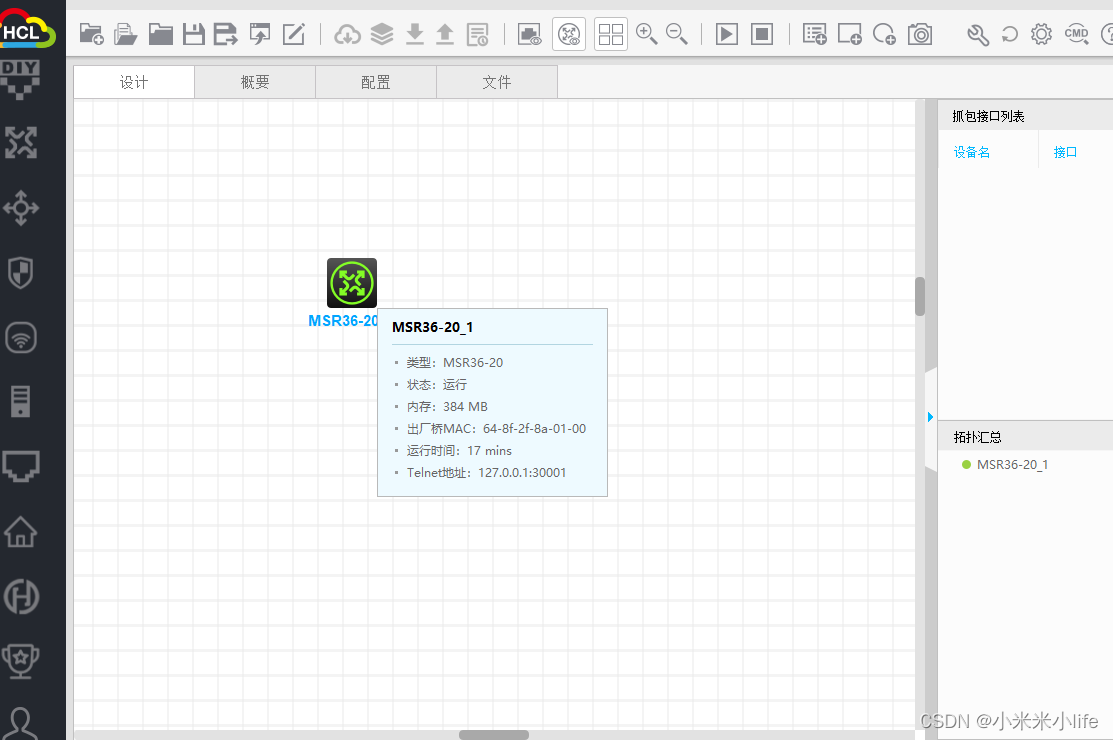
HCL设备启动失败——已经解决
摸索了一个多小时,终于搞定了,首先HCL这款软件是需要安装Oracle VM Visual Box的,小伙伴们安装的时候记得点击安装Visual Box; 安装完后显示设备不能启动,然后我根据这个 HCL模拟器中Server设备启动失败的解决办法_hc…...
RabbitMQ的幂等性、优先级队列和惰性队列
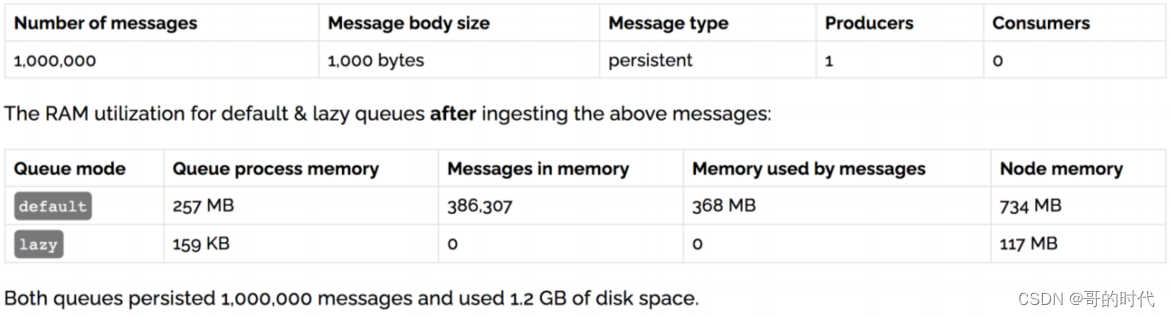
文章目录 一、幂等性1、概念2、消息重复消费3、解决思路4、消费端的幂等性保障5、唯一 ID指纹码机制6、Redis 原子性 二、优先级队列1、使用场景2、如何添加3、实战 三、惰性队列1、使用场景2、两种模式3、内存开销对比 总结 一、幂等性 1、概念 用户对于同一操作发起的一次请…...
Uniapp-小程序自定义导航栏
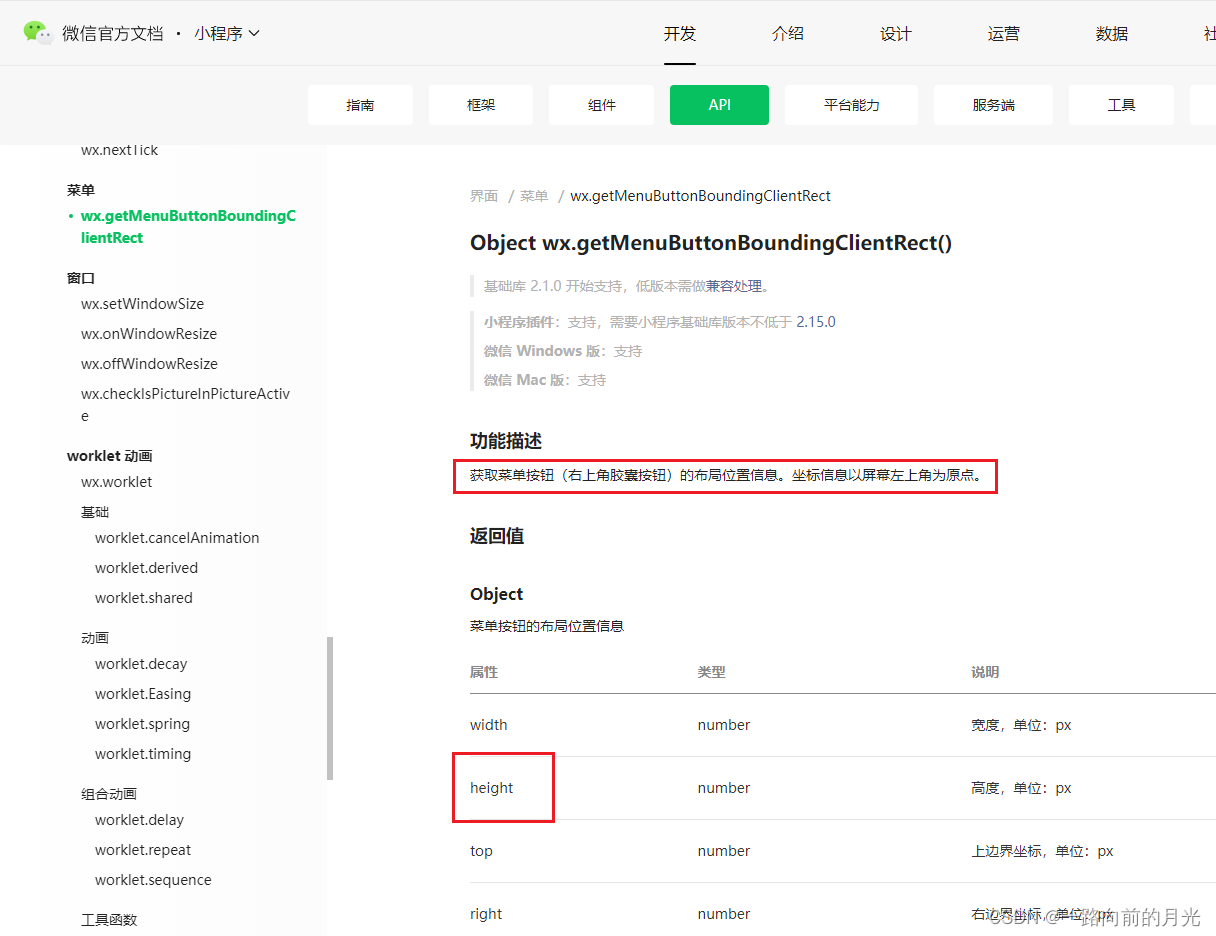
一、项目背景 制作小程序页面时候发现原生导航栏有一定的高度是没有背景渲染的会出现这种情况 但是我们需要的是 二、原因 小程序的原生导航栏存在。一般可以使用 纯色填充顶部栏 可以直接使用navigationBarBackgroundColor完成 在style中添加 "navigationBarBackgrou…...
云课五分钟-08安装Opera成功-仓库中查找对应版本
前篇: 云课五分钟-07安装Opera失败-版本不匹配 视频: 云课五分钟-08安装Opera成功-仓库中查找对应版本 文本: 最佳的途径就是使用系统内置的FireFox。 这么折腾的主要是为了演示安装一个第三方程序可能遇到的问题,并给出一些思…...
设计师的好帮手!在线PS网页版工具让创意无限发挥!
PS已经成为设计师必备的基本技能软件。PS版本的不断更新升级使PS功能更加强大。PS可以完成从简单的艺术家到复杂的设计和插画。但与此同时,PS也有设计师经常批评的痛点:大文件运行时内存卡住,位图放大后清晰度低,无穷无尽的快捷键,…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
