《洛谷深入浅出进阶篇》P1995 程序自动分析——并查集,离散化
上链接:P1955 [NOI2015] 程序自动分析 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P1955
https://www.luogu.com.cn/problem/P1955
上题干:
首先给你一个整数t,代表t次操作。
每一次操作包含以下内容:
1.给你一个整数n,让你执行n次条件
接下来n行,每行给你3个整数i,j,k,
例如 1 2 1
或 1 2 0
(前面两个数代表下标,第三个整数k代表条件,如果它是1 ,则代表 x1 = x2,如果它是0,代表x1!=x2)
然后我们每一次操作需要输出yes 或 no 来表示这n个条件是否全部成立。
(假如给出这样的数据:
n=4
1 2 1
2 3 1
1 4 1
3 4 0
第一个条件到第四个条件分别是 x1=x2,x2=x3,x1=x4 ,x3!=x4
由于前面三个条件我们可以得知 x1=x2=x3=x4 所以与x3!=x4矛盾,输出no)
数据 n<=1e6, i,j<=1e9
很显然,这道题的条件和数据范围告诉我们:需要用到并查集+(离散化 or hash表)
第一,并差集的特点就是能将不同的集合连接到一起,然后便于我们查询某两个元素是否为同一集合。
第二,这道题的数据范围太大了,i能达到ie9,所以我们直接用并查集的话,毫无疑问,数组装不下。所以我们可以用离散化来大大缩小数据范围,除此之外呢,我们还可以用hash表来处理这样的大数据,使得每一个大数据都有一个特别的标记与之对应。
这两种方法都满足我们的需求,这里主要用离散化来实现代码。
还记得离散化的具体步骤吗?
记录散点,排序,去重,二分查找
并查集的具体步骤呢?
初始化集合,建立查询函数,合并函数。
所以我们的思路是这样的:
1,先将每一次的散点都存入一个数组b中
2,对这个数组b进行排序
3,对这个数组进行去重(可以选择重新建立一个数组c来存放去重后的数据,也可以直接用unique函数。)
4,二分查找每一对散点的相对位置。
5,初始化并查集
6,如果第三个数字k=1,我们就利用并查集来合并两个集合。
7,如果第三个数字k=0,我们就查询两个数是否为同一集合,如果是同一集合,那么我们有
上代码:
const int MAXN = 1e6 + 10;
struct st {int x, y, z;
};
st a[MAXN];//三组输入数据存放之处
int b[2 * MAXN];// 存入散点
int c[2 * MAXN];//排序数组
int fa[2 * MAXN];//并查集
int btop, ctop;int find1(int x)
{if (x == fa[x])return fa[x];return fa[x] = find1(fa[x]);
}
void join1(int c1, int c2)
{int f1 = find1(c1), f2 = find1(c2);if (f1 != f2)fa[f1] = f2;
}
int main()
{int t;cin >> t;while (t--){btop = 0;ctop = 0;int n;cin >> n;for (int i = 1; i <= n; i++){cin >> a[i].x >> a[i].y >> a[i].z;b[++btop] = a[i].x;b[++btop] = a[i].y;}sort(b + 1, b + 1 + btop);for (int i = 1; i <= btop; i++)if (i == 1 or b[i] != b[i - 1])c[++ctop] = b[i];for (int i = 1; i <= n; i++){a[i].x = lower_bound(c + 1, c + 1 + ctop, a[i].x) - c;a[i].y = lower_bound(c + 1, c + 1 + ctop, a[i].y) - c;}for (int i = 1; i <= ctop; i++){fa[i] = i;}for (int i = 1; i <= n; i++){if(a[i].z)join1(a[i].x, a[i].y);}bool fk = 1;for (int i = 1; i <= n; i++){if (a[i].z==0){if (find1(a[i].x) == find1(a[i].y))fk = 0;}}if (fk == 0)cout << "NO" << endl;else cout << "YES" << endl;}
}相关文章:
《洛谷深入浅出进阶篇》P1995 程序自动分析——并查集,离散化
上链接:P1955 [NOI2015] 程序自动分析 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P1955 上题干: 首先给你一个整数t,代表t次操作。 每一次操作包含以下内容: 1.给你一个整数n,让…...

基于单片机的自动循迹小车(论文+源码)
1.系统设计 此次基于单片机的自动循迹小车的设计系统,结合循迹模块来共同完成本次设计,实现小车的循迹功能,其其整体框架如图2.1所示。其中,采用STC89C52单片机来作为核心控制器,负责将各个传感器等模块链接起来&…...

linux系统中安装python到指定目录
Linux系统中安装python 下载Python源码包 根据服务器系统和需要的Python版本,在Python官网下载对应的Python源码包。 安装依赖(需要权限) yum install gcc gcc-c patch libffi-devel python-devel zlib-devel bzip2-devel openssl-devel…...
分布式事务 - seata安装
分布式事务 - seata 一、本地事务与分布式事务 1.1、本地事务 本地事务,也就是传统的单机事务。在传统数据库事务中,必须要满足四个原则(ACID)。 1.2、分布式事务 分布式事务,就是指不是在单个服务或单个数据库架构…...
CentOS to 浪潮信息 KeyarchOS 迁移体验与优化建议
浪潮信息KeyarchOS简介 KeyarchOS即云峦操作系统(简称KOS), 是浪潮信息研发的一款面向政企、金融等企业级用户的 Linux 服务器操作系统。它基于Linux内核、龙蜥等开源技术,支持x86、ARM 等主流架构处理器,其稳定性、安全性、兼容性和性能等核心能力均已…...

Go解析soap数据和修改其中数据
一、解析soap数据 package main import ("fmt" "encoding/xml" ) type Envelope struct { XMLName xml.Name Header Header } type Header struct { XMLName xml.Name xml:"Header" Security Security xml:"Security" } type Secu…...

LeetCode98. Validate Binary Search Tree
文章目录 一、题目二、题解 一、题目 Given the root of a binary tree, determine if it is a valid binary search tree (BST). A valid BST is defined as follows: The left subtree of a node contains only nodes with keys less than the node’s key. The right sub…...

【LeetCode】206. 反转链表
206. 反转链表 难度:简单 题目 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2: 输入:head [1,2] 输…...

飞天使-通过GET 和POST进案例演示
文章目录 GETPOST GET def index(request):# 在url中获取学号sno request.GET.get("sno", None)print("学号为:",sno)# 判断学号如果有值,执行查询if sno:results get_student_by_sno(sno)# 展示在页面return render(request, ind…...
【MySql】12- 实践篇(十)
文章目录 1. 为什么临时表可以重名?1.1 临时表的特性1.2 临时表的应用1.3 为什么临时表可以重名?1.4 临时表和主备复制 2. MySql内部临时表使用场景2.1 union 执行流程2.2 group by 执行流程2.3 group by 优化方法 -- 索引2.4 group by 优化方法 -- 直接排序 3. Me…...

<C++> 反向迭代器
我们知道正向迭代器的设计:begin迭代器指向第一个数据,end迭代器指向最后一个数据的下一个位置 。移向下一个数据,解引用得到数据的值,并根据容器储存方式的不同,容器有不同类型的迭代器。 注意:rbegin迭代…...

【EI会议征稿】第三届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2024)
第三届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2024) 2024 3rd International Conference on Cyber Security, Artificial Intelligence and Digital Economy 第三届网络安全、人工智能与数字经济国际学术会议(CSAIDE 2024&#…...

格力报案称“高管遭自媒体侮辱诽谤”
我是卢松松,点点上面的头像,欢迎关注我哦! 王自如的一番话引来了众多围攻,格力已报警,高管遭到侮辱诽谤。这应该是近年来少见的大企业和网络大v之间公开翻脸互撕的场景了! 就在今天格力就高管遭自媒体侮辱诽谤报案。…...

HBase之Compaction
目录 Compaction触发条件相关参数 文件选取策略ExploringCompactionPolicy常见优化 Compaction 随着memstore的不断flush,storefile的数量将会不断增加。compaction将通过合并storefile来减少文件数量,并提高读性能。conpaction以store为单位 Compacti…...

设计模式之结构型模式
这些模式关注对象之间的组合和关联方式,以便形成更大的结构和功能。 适配器模式(Adapter Pattern)桥接模式(Bridge)装饰器模式(Decorator)组合模式(Composite)外观模式&a…...

centOs 6.10 编译 qt 5.15.11
安装依赖库 xcb 依赖库 qt xcb 需要的依赖 如何要用 x11, 就要在编译的时候加上 -xcb 选项,就要安装 xcb 相关的库。 到时可以在 config.log 文件查看,缺少哪个库就安装哪个。 下面是我手动安装的库和对应版本: xcb-proto-1.14.tar.gz x…...
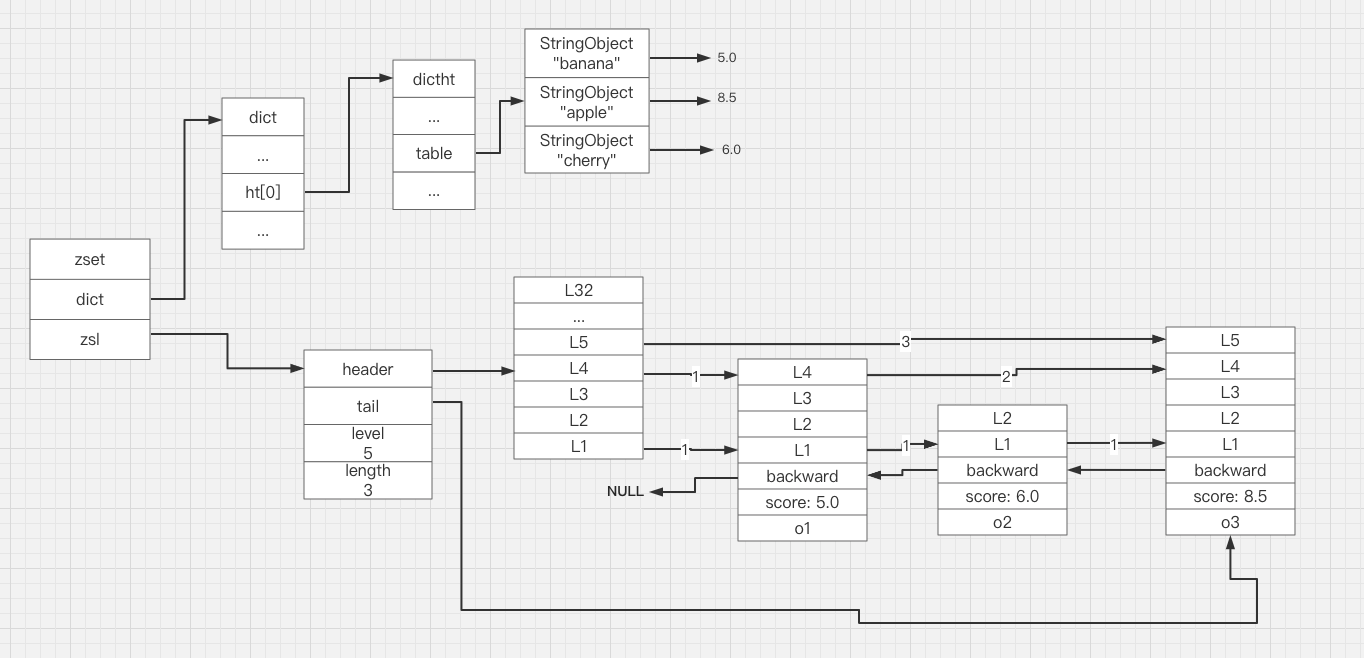
Redis对象的数据结构及其原理汇总
本文首发于公众号:Hunter后端 原文链接:Redis对象的数据结构及其底层实现原理汇总 当我们被问到 Redis 中有什么数据结构,或者说数据类型,我们可能会说有字符串、列表、哈希、集合、有序集合。 其实这几种数据类型在 Redis 中都由…...

@RestController 注解网页返回 [] ,出现的bug
RestController 注解网页返回 [] ,出现的bug RestController RequestMapping("emp") public class EmployeeController {Autowiredprivate EmployeeService employeeService;GetMapping("find")public List<Employee> find(){List<Employee> …...
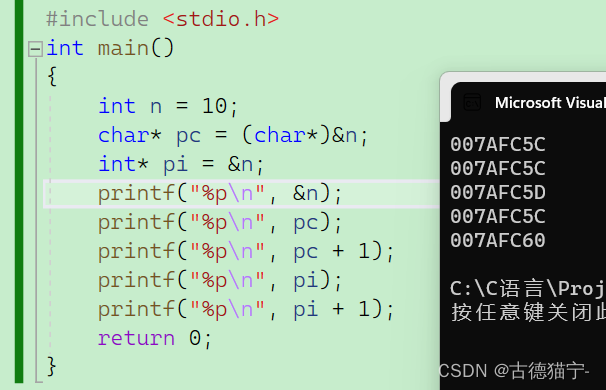
C语言指针详解(1)(能看懂字就能明白系列)文章超长,慢慢品尝
目录 1、内存和地址 2、指针简介 与指针相关的运算符: 取地址操作符(&) 解引用操作符(间接操作符)(*) 编辑 指针变量的声明 指针变量类型的意义 指针的基本操作 1、指针与整数相加…...

为什么别人年薪30W+?同样为测试人,“我“的测试之路...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、软件测试员&am…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
