代码随想录算法训练营第五十五天丨 动态规划part16
583. 两个字符串的删除操作
思路
#动态规划一
本题和动态规划:115.不同的子序列 (opens new window)相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解,动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
- 确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
- dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
dp[0][j]的话同理,所以代码如下:
int[][] dp = new int[word1.length() + 1][word2.length() + 1];for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;- 确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
- 举例推导dp数组
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
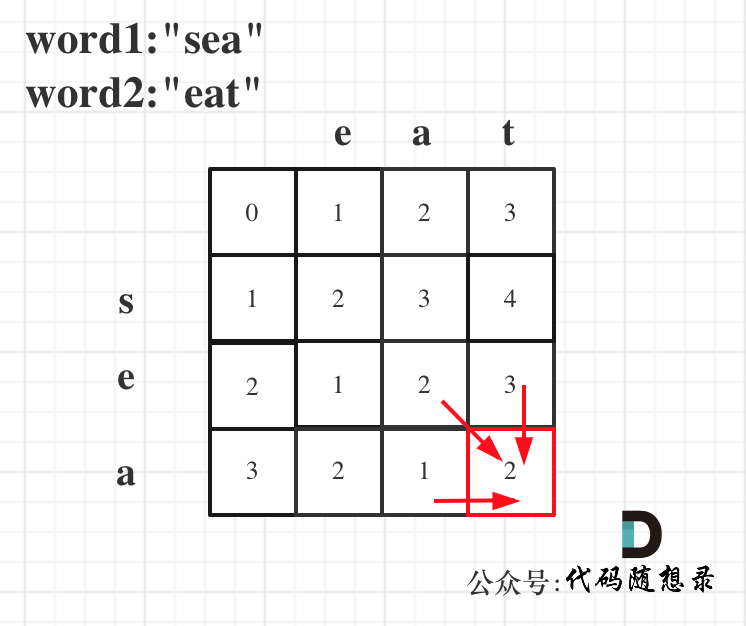
以上分析完毕,代码如下:
// dp数组中存储需要删除的字符个数
class Solution {public int minDistance(String word1, String word2) {int[][] dp = new int[word1.length() + 1][word2.length() + 1];for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;for (int i = 1; i < word1.length() + 1; i++) {for (int j = 1; j < word2.length() + 1; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];}else{dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));}}}return dp[word1.length()][word2.length()];}
}- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
#动态规划二
本题和动态规划:1143.最长公共子序列 (opens new window)基本相同,只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
代码如下:
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1 + 1][len2 + 1];for (int i = 1; i <= word1.length(); i++) {for (int j = 1; j <= word2.length(); j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}int len = dp[len1][len2];return len1 + len2 - 2 * len;}
}- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
72. 编辑距离
思路
编辑距离终于来了,这道题目如果大家没有了解动态规划的话,会感觉超级复杂。
编辑距离是用动规来解决的经典题目,这道题目看上去好像很复杂,但用动规可以很巧妙的算出最少编辑距离。
接下来依然使用动规五部曲,对本题做一个详细的分析:
#1. 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
为什么这么定义卡哥在 718. 最长重复子数组 (opens new window)中做了详细的讲解。
其实用i来表示也可以! 用i-1就是为了方便后面dp数组初始化的。
#2. 确定递推公式
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换
也就是如上4种情况。
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
此时可能有同学有点不明白,为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
在下面的讲解中,如果哪里看不懂,就回想一下dp[i][j]的定义,就明白了。
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了,怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:
a a d+-----+-----+ +-----+-----+-----+| 0 | 1 | | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
递归公式代码如下:
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
#3. dp数组如何初始化
再回顾一下dp[i][j]的定义:
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
所以C++代码如下:
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
#4. 确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
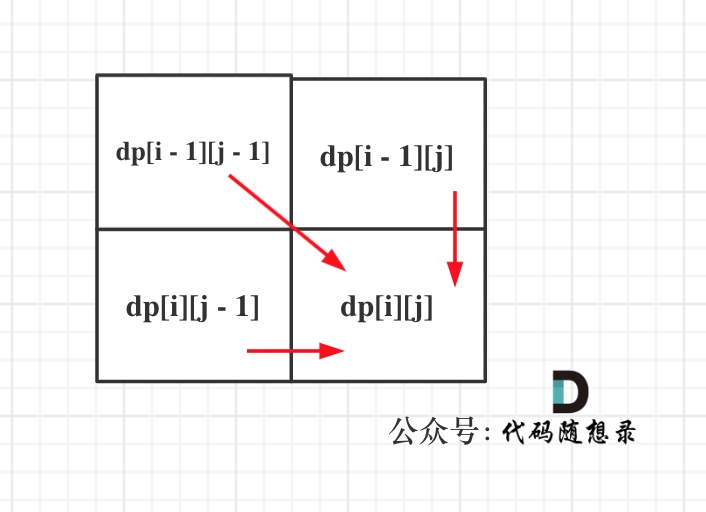
所以在dp矩阵中一定是从左到右从上到下去遍历。
代码如下:
for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;}}
}
#5. 举例推导dp数组
以示例1为例,输入:word1 = "horse", word2 = "ros"为例,dp矩阵状态图如下:
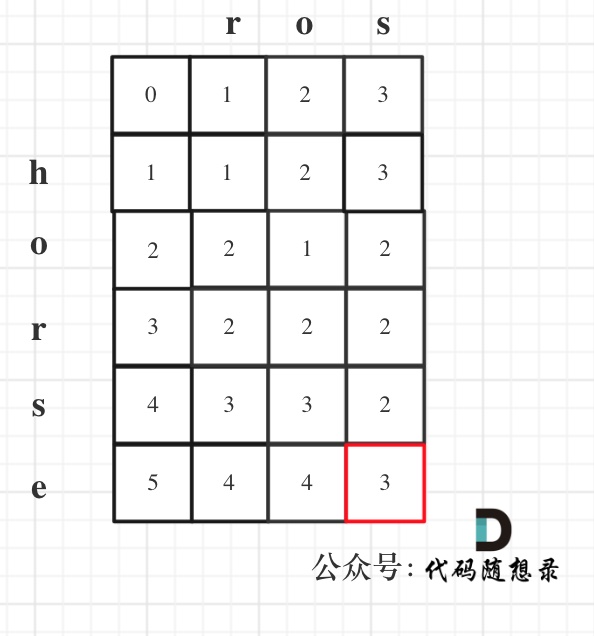
以上动规五部分析完毕,代码如下:
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1 + 1][len2 + 1];//初始化for (int i = 0; i <= len1; i++) dp[i][0]=i;for (int j = 0; j <= len2; j++) dp[0][j]=j;for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1],dp[i-1][j-1]))+1;}}}return dp[len1][len2];}
}- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
相关文章:

代码随想录算法训练营第五十五天丨 动态规划part16
583. 两个字符串的删除操作 思路 #动态规划一 本题和动态规划:115.不同的子序列 (opens new window)相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。 这次是两个字符串可以相互删了,这…...

【Linux】kernel与应用消息队列的一种设计
Linux进程间通讯的方式有很多种,这里介绍一种通过消息队列的方式来实现kernel与APP之间的消息收发实现方式,这种方式特别适用于,kernel中发送消息,应用层收取消息。 消息队列设备驱动 该方法的设计思路即是创建一个消息队列的设…...

我们常说的网络资产,具体是如何定义的?
文章目录 什么叫网络资产?官方定义的网络资产网络资产数字化定义推荐阅读 什么叫网络资产? 通过百度查询搜索什么叫网络资产?大体上都将网络资产归类为计算机网络中的各类设备。 基本上会定义网络传输通信架构中用到的主机、网络设备、防火…...

WPF中可冻结对象
在WPF(Windows Presentation Foundation)中,"可冻结对象"指的是那些在创建之后可以被设置为不可更改状态的对象。这种特性允许这些对象更有效地被共享和复制,并且可以增加性能。 例如,Brushes,P…...
【人工智能实验】A*算法求解8数码问题 golang
人工智能经典问题八数码求解 实际上是将求解转为寻找最优节点的问题,算法流程如下: 求非0元素的逆序数的和,判断是否有解将开始状态放到节点集,并设置访问标识位为true从节点集中取出h(x)g(x)最小的节点判断取出的节点的状态是不…...
Kafka学习笔记(二)
目录 第3章 Kafka架构深入3.3 Kafka消费者3.3.1 消费方式3.3.2 分区分配策略3.3.3 offset的维护 3.4 Kafka高效读写数据3.5 Zookeeper在Kafka中的作用3.6 Kafka事务3.6.1 Producer事务3.6.2 Consumer事务(精准一次性消费) 第4章 Kafka API4.1 Producer A…...
Typora for Mac:打造全新文本编辑体验
Typora for Mac是一款与众不同的文本编辑器,它不仅拥有直观易用的界面,还融合了Markdown语法和富文本编辑的功能,为用户带来了前所未有的写作和编辑体验。 一、简洁明了的界面设计 Typora for Mac的界面简洁明了,让用户可以专注…...

TikTok与媒体素养:如何辨别虚假信息?
在当今数字时代,社交媒体平台如TikTok已经成为信息传播和社交互动的主要渠道之一。然而,随之而来的是虚假信息的泛滥,这对用户的媒体素养提出了严峻的挑战。本文将探讨TikTok平台上虚假信息的现象,以及如何提高媒体素养࿰…...
Spring Boot 中使用 ResourceLoader 加载资源的完整示例
ResourceLoader 是 Spring 框架中用于加载资源的接口。它定义了一系列用于获取资源的方法,可以处理各种资源,包括类路径资源、文件系统资源、URL 资源等。 以下是 ResourceLoader 接口的主要方法: Resource getResource(String location)&am…...
1688往微信小程序自营商城铺货商品采集API接口
一、背景介绍 随着移动互联网的快速发展,微信小程序作为一种新型的电商形态,正逐渐成为广大商家拓展销售渠道、提升品牌影响力的重要平台。然而,对于许多传统企业而言,如何将商品信息快速、准确地铺货到微信小程序自营商城是一个…...

QStatusBar开发详解
一、QStatusBar接口说明 QStatusBar 类是 Qt 中用于创建和管理状态栏的类。它继承自 QFrame 类,提供了在主窗口底部显示消息、进度等信息的功能。以下是一些 QStatusBar 类的重要接口: 1.1 QStatusBar构造函数 QStatusBar(QWidget *parent nullptr);…...

后端接口性能优化分析-程序结构优化
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码🔥如果感觉博主的文章还不错的话,请👍三连支持&…...
【SpringBoot3+Vue3】三【实战篇】-后端(优化)
目录 一、登录优化-redis 1、SpringBoot集成redis 1.1 pom 1.2 yml 1.3 测试程序(非必须) 1.4 启动redis,执行测试程序 2、令牌主动失效(代码优化) 2.1 UserController设置token到redis 2.2 登录拦截器Log…...
DevExpress中文教程 - 如何在macOS和Linux (CTP)上创建、修改报表(上)
DevExpress Reporting是.NET Framework下功能完善的报表平台,它附带了易于使用的Visual Studio报表设计器和丰富的报表控件集,包括数据透视表、图表,因此您可以构建无与伦比、信息清晰的报表。 DevExpress Reports — 跨平台报表组件&#x…...
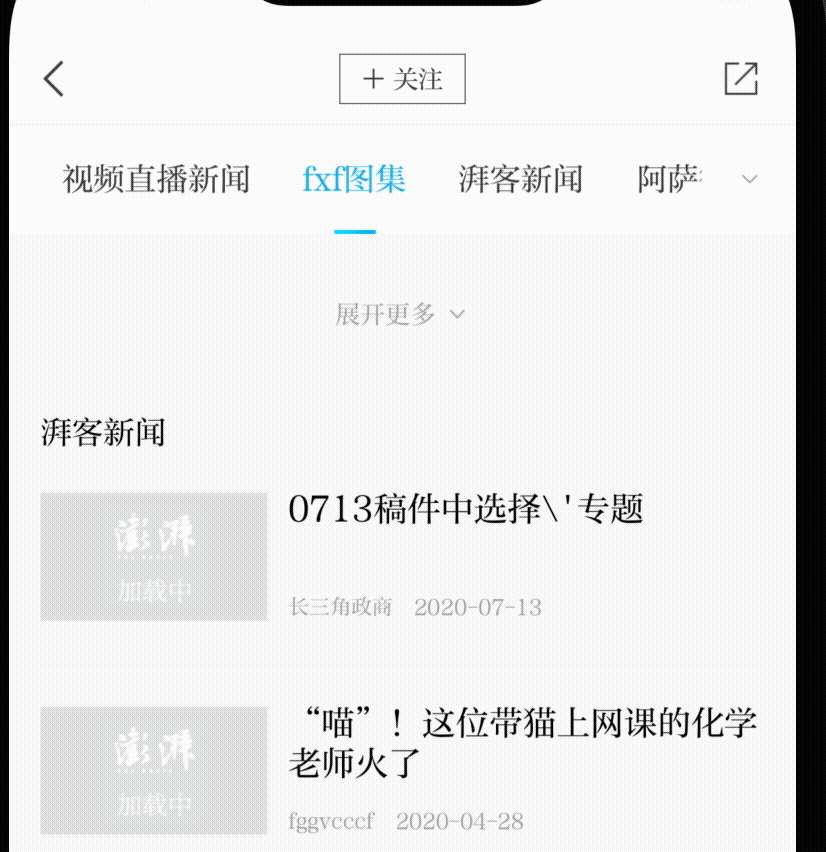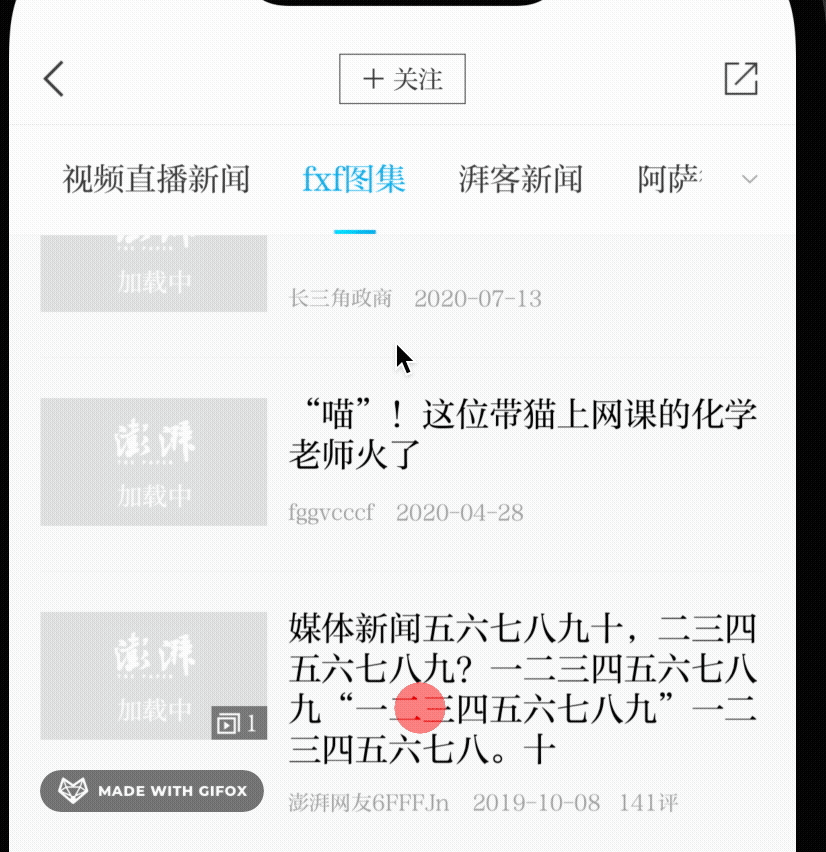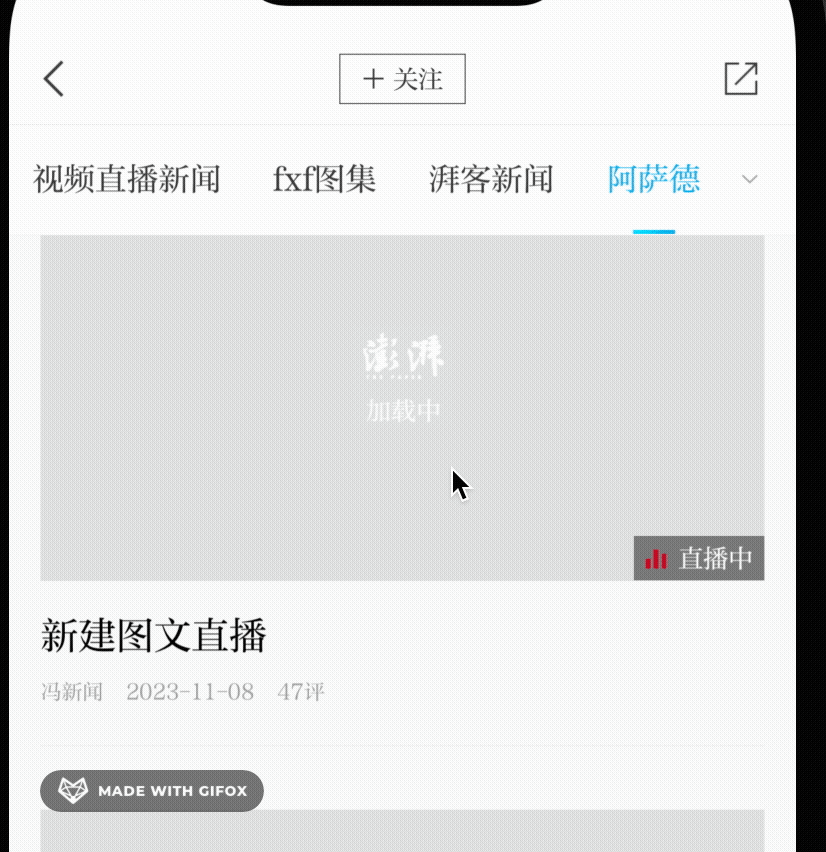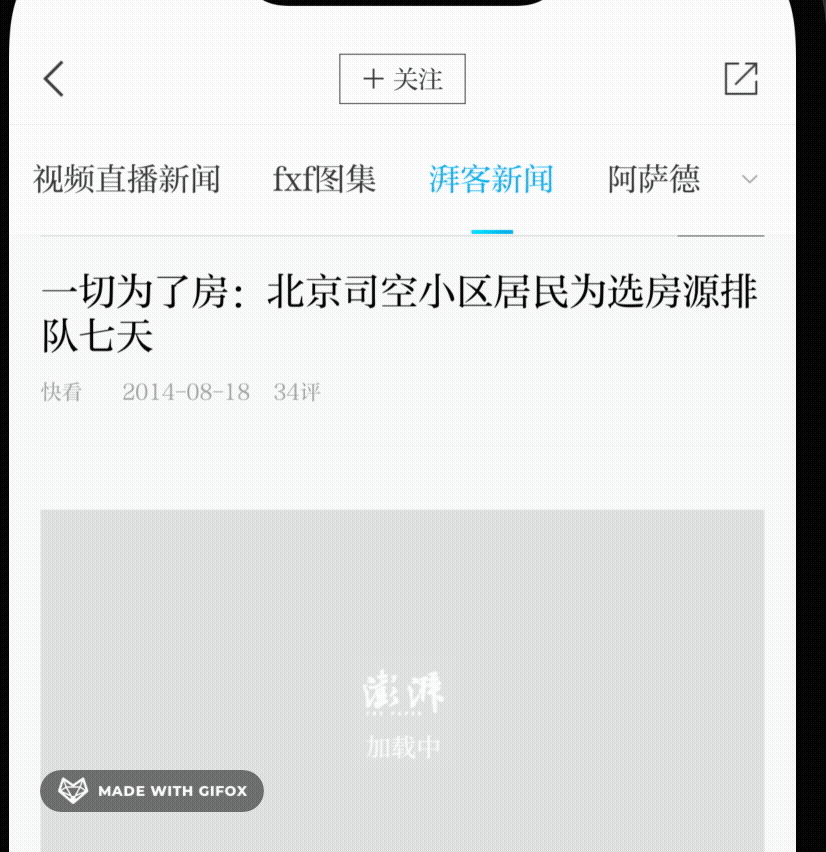
一个iOS tableView 滚动标题联动效果的实现
效果图 情景 tableview 是从屏幕顶部开始的,现在有导航栏,和栏目标题视图将tableView的顶部覆盖了 分析 我们为了达到滚动到某个分区选中标题的效果,就得知道 展示最顶部的cell或者区头在哪个分区范围内 所以我们必须首先获取顶部的位置 …...

代码执行相关函数以及简单例题
代码/命令 执行系列 相关函数 (代码注入)...
大数据爬虫分析基于Python+Django旅游大数据分析系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 基于Python和Django的旅游大数据分析系统是一种使用Python编程语言和Django框架开发的系统,用于处理和分…...

C# 结构体介绍
文章目录 定义结构体实例化结构体结构体的值类型特性结构体和类的区别限制 C# 中的结构体(Struct)是一种值类型数据结构,用于封装不同或相同类型的数据成一个单一的实体。结构体非常适合用来表示轻量级的对象,比如坐标点、颜色值或…...
【机器学习】特征工程:特征预处理,归一化、标准化、处理缺失值
特征预处理采用的是特定的统计方法(数学方法)将数据转化为算法要求的数字 1. 数值型数据 归一化,将原始数据变换到[0,1]之间 标准化,数据转化到均值为0,方差为1的范围内 缺失值,缺失值处理成均值、中…...

Pytorch torch.norm函数详解用法
torch.norm参数定义 torch版本1.6 def norm(input, p"fro", dimNone, keepdimFalse, outNone, dtypeNone)input input (Tensor): the input tensor 输入为tensorp p (int, float, inf, -inf, fro, nuc, optional): the order of norm. Default: froThe following …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
