《向量数据库指南》——TruLens + Milvus Cloud构建RAG深入了解性能
深入了解性能
-
索引类型
本例中，索引类型对查询速度、token 用量或评估没有明显影响。这可能是因为数据量较小的关系。索引类型对较大语料库可能更重要。
-
Embedding 模型
text-embedding-ada-002 在准确性(0.72，平均 0.60)和答案相关度(0.82，平均0.62)上优于 MiniLM Embedding 模型。两者在上下文相关度上表现一致。这个结果可能是 OpenAI Embedding 更适合百科信息的缘故。
-
相似度 top-K
top-k 的增加可以略微提高检索质量(通过上下文相关度测量)。检索的文本块越多，检索器获取高质量上下文的可能性越大。
top-K 的增加也改善了准确性(0.71，平均 0.62)和答案相关度(0.76，平均0.68)。检索更多上下文文本块可以为语言模型提供更多支持其结论的内容。但是更高的 top-K 意味着更高的 token 使用成本（每次调用平均需要额外使用 590 个 token）。
-
分块大
相关文章：
《向量数据库指南》——TruLens + Milvus Cloud构建RAG深入了解性能
深入了解性能 索引类型 本例中，索引类型对查询速度、token 用量或评估没有明显影响。这可能是因为数据量较小的关系。索引类型对较大语料库可能更重要。 Embedding 模型 text-embedding-ada-002 在准确性(0.72，平均 0.60)和答案相关度(0.82，平均0.62)上优于 MiniLM Embeddin…...
vscode代码上传到gitlab
打开终端 1.1输入一下内容提交到本地仓库 PS D:\VueProject2\mall-admin-web> git add . PS D:\VueProject2\mall-admin-web> git commit -m “商品优化，屏蔽不要内容” 1.2提交到远程仓库 master应该被替换为 Gitee 仓库中默认的分支名称 PS D:\VueProje…...
Spring Boot 项目的常用注解与依赖
工具类 lombok 依赖 可以快速的为类提供 get，set，toString 等方法 <dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional> </dependency> My…...
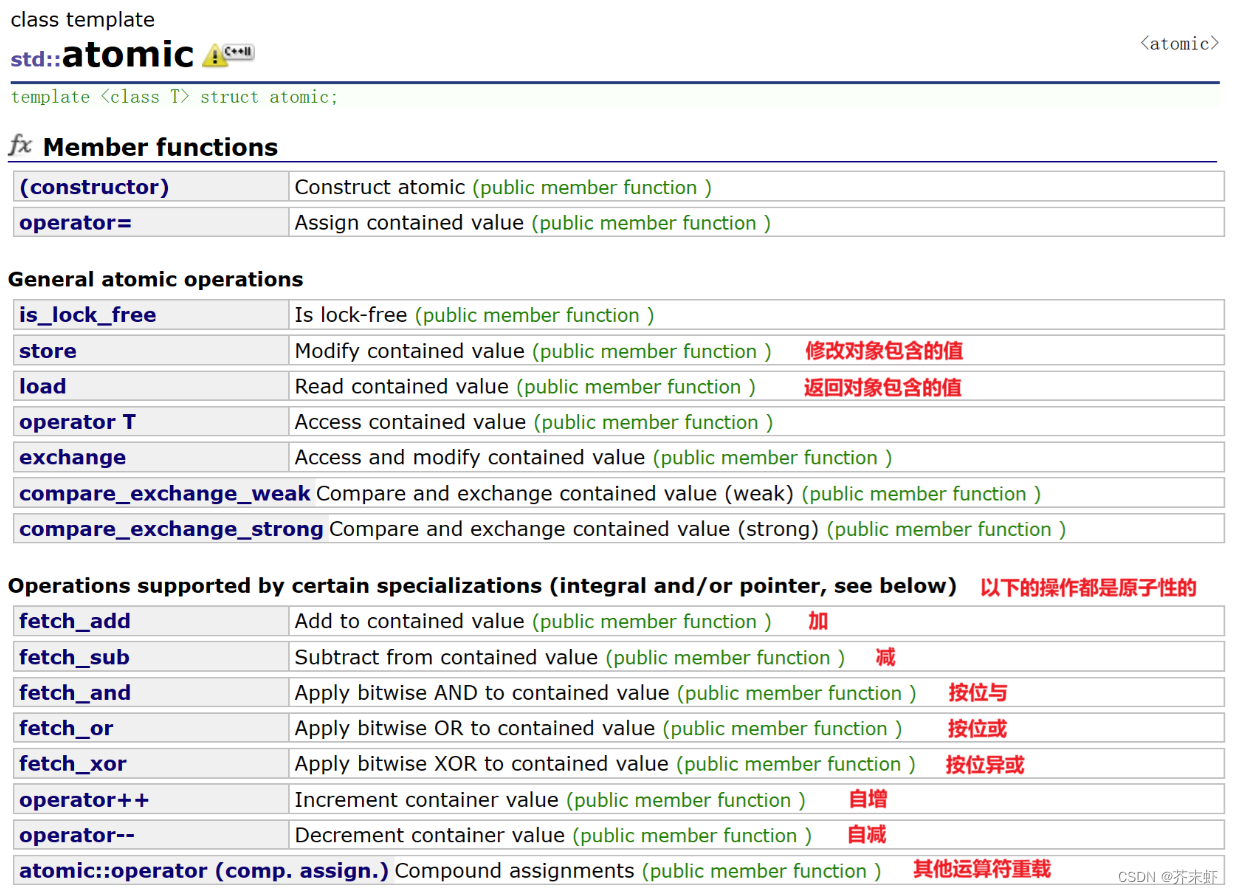
【C++11】多线程库 {thread线程库，mutex互斥锁库，condition_variable条件变量库，atomic原子操作库}
在C11之前，涉及到多线程问题，都是和平台相关的，比如windows和linux下各有自己的接口，这使得代码的可移植性比较差。 //在C98标准下，实现可移植的多线程程序 —— 条件编译 #ifdef _WIN32CreateThread(); //在windows系…...
智能导诊系统：基于机器学习和自然语言处理技术，可快速推荐合适的科室和医生
智能导诊系统是一种基于人工智能技术的新型系统，它能够为医院提供患者服务和管理，提高医院的管理效率和服务水平。 技术架构：springbootredismybatis plusmysqlRocketMQ 以下是智能导诊系统的应用场景和功能特点： 应用场景 1.患…...
如何防止图片抖动
如何防止图片抖动 什么是图片抖动，就是我们加载图片完成之后，图片显示，但是其下方内容会跟着下移，这就造成了图片抖动用户体验不好，我们想即使图片没加载出来，页面上也有一个空白的位置留给图片。 我们要知…...
依赖注入方式
依赖注入方式 思考：向一个类中传递数据的方式有几种？ 普通方法（set方法）构造方法 思考：依赖注入描述了在容器中建立bean与bean之间关系依赖的过程，如果bean运行需要的是数字或字符串呢？ 引用类…...
HTML 超链接 a 标签
在 HTML 标签中，a 标签用于定义超链接，作用是从一个页面链接到另一个页面。 在 a 标签中有两个常用的属性： - href 属性，用于指定链接目标的 url 地址（必须属性）。当为标签应用 href 属性时，…...
【cpolar】Ubuntu本地快速搭建web小游戏网站，公网用户远程访问
🎥 个人主页：深鱼~🔥收录专栏：cpolar🌄欢迎 👍点赞✍评论⭐收藏 目录 前言 1. 本地环境服务搭建 2. 局域网测试访问 3. 内网穿透 3.1 ubuntu本地安装cpolar 3.2 创建隧道 3.3 测试公网访问 4. 配置…...
数字化企业需要什么样的数据中心
随着科技的迅猛发展和数字化浪潮的涌现，企业越来越依赖于强大而高效的数据中心来支持其业务运营和创新发展。数字化企业需要一个先进的、灵活可扩展的数据中心来满足不断增长的数据需求、提高业务灵活性和确保安全性。 以下是数字化企业需要考虑的关键因素…...
el-table固定表头（设置height）出现内容过多时不能滚动问题
主要原因是el-table没有div包裹 解决：加一个div并设置其高度和overflow 我自己的主要代码 <div class"contentTable"><el-tableref"table":data"tableData"striperow-dblclick"onRowDblclick"height"100%&q…...
从流程优化到经营提效，法大大电子签全面助力智慧零售升级
在新零售模式下，“商业综合体、百货商场、连锁商超、连锁便利店、线上电商平台”等各类商业零售企业借助数字化的手段来改造和重塑传统零售流程和逻辑，实现全面数字化转型，包括线上线下一体化、全场景覆盖、全链条联通、全渠道经营、客户服务…...
Jquery 通过class名称属性，匹配元素
UI自动化过程中，常常需要判断某个元素是否满足条件，再走不通的脚本逻辑；、本文介绍如何通过jquery判断菜单是否展开，来决定是否执行菜单展开脚本；Jquery通过class名称属性，匹配元素 我们先分析，…...
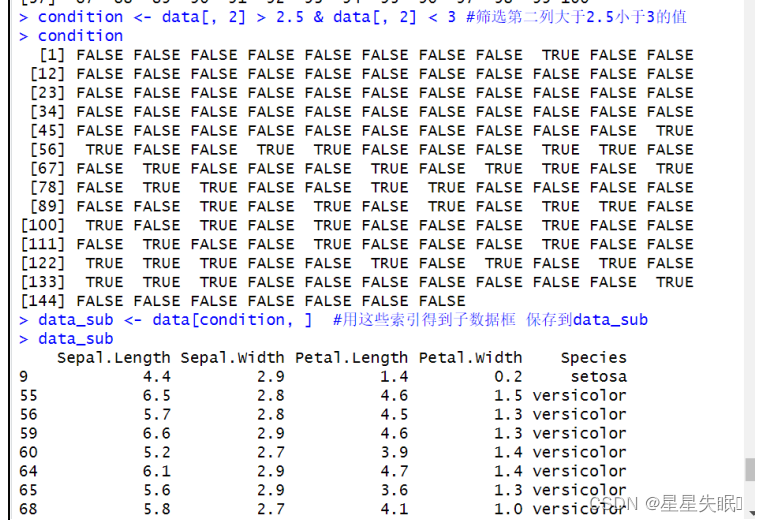
复杂数据统计与R语言程序设计实验二
1、创建一个对象，并进行数据类型的转换、判别等操作，步骤如下。 ①使用命令清空工作空间，创建一个对象x，内含元素为序列：1，3，5，6，8。 ②判断对象x是否为数值型数据。 ③…...
打印. 2023-11-18)
python3:print()打印. 2023-11-18
Python3 print ()不换行输出 import random # 导入random for i in range(10):print(random.randint(1,999), end",") #random.randint(1,999)随机返回1-999间任意一个整数,包括1和999 #print()添加end"" 自定义参数，实现不换行输出效果.end的…...
ARM 版 Kylin V10 部署 KubeSphere 3.4.0 不完全指南
前言 知识点 定级：入门级KubeKey 安装部署 ARM 版 KubeSphere 和 KubernetesARM 版麒麟 V10 安装部署 KubeSphere 和 Kubernetes 常见问题 实战服务器配置 (个人云上测试服务器) 主机名IPCPU内存系统盘数据盘用途ksp-master-1172.16.33.1681650200KubeSphere/k8…...
二元分类模型评估方法
文章目录 前言一、混淆矩阵二、准确率三、精确率&召回率四、F1分数五、ROC 曲线六、AUC（曲线下面积）七、P-R曲线类别不平衡问题中如何选择PR与ROC 八、 Python 实现代码混淆矩阵、命中率、覆盖率、F1值ROC曲线、AUC面积 指标 公式 意义 真正例 (TP)被…...
专业数据标注公司：景联文科技领航数据标注行业，满足大模型时代新需求
随着大模型的蓬勃发展和相关政策的逐步推进，为数据要素市场化配置的加速推进提供了有力的技术保障和政策支持。数据要素生产力度的不断提升，为数据标注产业带来了迅速发展的契机。 根据国家工信安全发展研究中心测算，2022年中国数据加工环节的…...
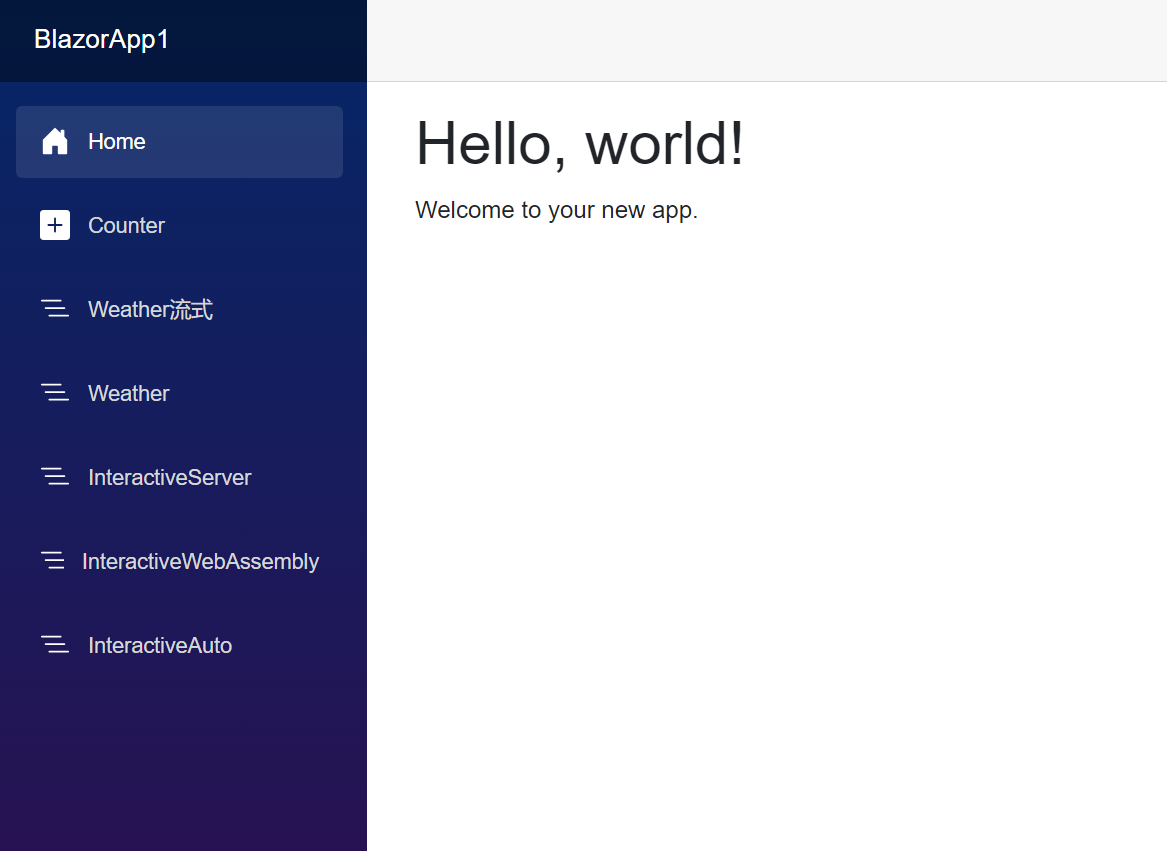
.Net8 Blazor 尝鲜
全栈 Web UI 随着 .NET 8 的发布，Blazor 已成为全堆栈 Web UI 框架，可用于开发在组件或页面级别呈现内容的应用，其中包含： 用于生成静态 HTML 的静态服务器呈现。使用 Blazor Server 托管模型的交互式服务器呈现。使用 Blazor W…...
Vue.js 页面加载时触发函数
使用 Vue 的生命周期钩子函数： 在 Vue 组件中，可以使用生命周期钩子函数来执行特定的代码。其中，mounted 钩子函数可以在组件被挂载到 DOM 后触发。 <template><div><!-- 页面内容 --></div> </template>expo…...
C++：std::is_convertible
C++标志库中提供is_convertible，可以测试一种类型是否可以转换为另一只类型： template <class From, class To> struct is_convertible; 使用举例： #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了：一行…...
UE5 学习系列（三）创建和移动物体
这篇博客是该系列的第三篇，是在之前两篇博客的基础上展开，主要介绍如何在操作界面中创建和拖动物体，这篇博客跟随的视频链接如下： B 站视频：s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
P3 QT项目----记事本（3.8）
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得，如果用户端访问量比较大，数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据，减少数据库查询操作。 缓存逻辑分析： ①每个分类下的菜品保持一份缓存数据…...
【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类：块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
ip子接口配置及删除
配置永久生效的子接口，2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理）
上一章用到了V2 的概念，其实 Fiori当中还有 V4，咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务)，代理中间件（ui5-middleware-simpleproxy）-CSDN博客…...
（一）单例模式
一、前言 单例模式属于六大创建型模式，即在软件设计过程中，主要关注创建对象的结果，并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计，从而隐藏了类对象的实例是如何被创建的，封装了软件系统使用的具体对象类型。 六大创建型模式包括…...