整形数据和浮点型数据在内存中的存储差别
愿所有美好如期而遇

我们先来看代码,猜猜结果是什么呢?
int main()
{//以整型数据的方式存储int n = 10;float* m = (float*)&n;//以整型数据的方式读取printf("%d\n", n);//以浮点型数据的方式2读取printf("%f\n", *m);printf("----------------------------\n");//以浮点型数据的方式存储*m = 10.0;//以整型数据的方式读取printf("%d\n", n);//以浮点型数据的方式读取printf("%f\n", *m);return 0;
}
你是不是觉得答案是10 10.0 10 10.0 呢?
那么我们接下来解释一下为什么是上面那个结果
首先,整型数据和浮点型数据在内存中的存储方式是不同的
(1)整型数据的存储方式是怎样的呢?
在看下面的解释前,如果看不懂请参考:原码,反码,补码,char大小范围的解释
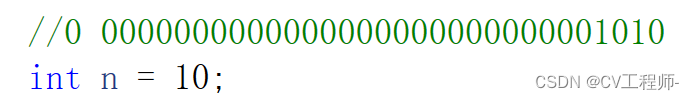
整型数据在内存中直接转换为二进制后以补码形式存储。
(2)浮点型数据的存储方式是怎样的呢?
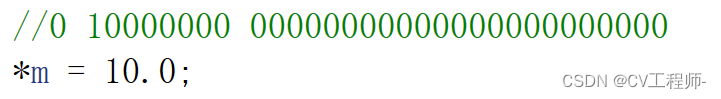
我们要对他的二进制分三部分去看,符号位,指数位,有效数字位(已经用空格分开)
10.0我们可以写成(-1)^0 *1.0*10^1,(-1)^0,0就是符号位,正数为0,负数为1,1.0就是我们的有效数字,10^1,1就是我们的指数,但是float类型的数据指数在存储时需要加上127,double类型的数据指数在存储时要加上1023,这是IEE754的规定。
而且他还规定了float的指数位有8位,有效数字位23,double指数位有11位,有效数字位52位。数位为unsigned int类型,恒为正数。
指数为1 + 127 ,也就是128,转换为二进制也就是10000000,而有效数字位不存储1,在读取数据时自动前面补1,这样就节省了一位去存储有效数字,也就提高了精度。
读取数据时如何读取?分三种情况:
一:指数位不是全0也不是全1
好比我们上面的10的二进制,我们读取时如何读取?
先看符号位,是正数,然后看指数位,指数位减去127,也就剩下1,也就是10^1,再看有效数字位,全是0,也就是1.0000......,最后我们乘起来:(-1)^0 * 10^1 * 1.0
二:指数位全是0
那也就相当于我们原来的指数是-127,加上127后为0,那么指数位就是10^-127,这时,我们在读取时就丢掉有效数字位本来会加的那个1,直接用符号位乘指数以及后面的有效数字位。
三:指数位全是1
也就相当于是128+127,我们原本的指数位就是128,也就是10^128,表示一个非常大的数据。
相关文章:
整形数据和浮点型数据在内存中的存储差别
愿所有美好如期而遇 我们先来看代码,猜猜结果是什么呢? int main() {//以整型数据的方式存储int n 10;float* m (float*)&n;//以整型数据的方式读取printf("%d\n", n);//以浮点型数据的方式2读取printf("%f\n", *m);printf(&…...
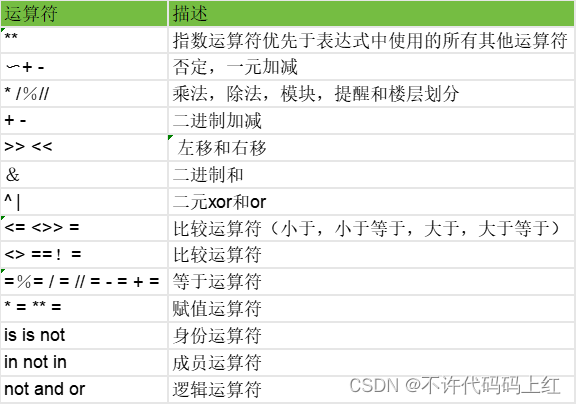
【Python基础篇】运算符
博主:👍不许代码码上红 欢迎:🐋点赞、收藏、关注、评论。 格言: 大鹏一日同风起,扶摇直上九万里。 文章目录 一 Python中的运算符二 算术运算符1 Python所有算术运算符的说明2 Python算术运算符的所有操作…...

开启数据库审计 db,extended级别或os级别)并将审计文件存放到/opt/oracle/audit/下
文章目录 1、登录到数据库2、查看审计状态3、创建审计目录4、启用审计5、设置审计文件路径6、再次查看结果 1、登录到数据库 使用SQL*Plus或者其他Oracle数据库客户端登录到数据库。 sqlplus / as sysdba;2、查看审计状态 show parameter audit;目前是DB状态,并且…...

02.webpack中多文件打包
1.module,chunk,bundle的区别 moudle - 各个源码文件,webpack中一切皆是模块chunk - 多模块合并成的,如entry, import(), splitChunkbundle - 最终的输出文件 2.多文件打包配置 2.1 webpack.common.js const path require(path) const HtmlWebpackPl…...

IEEE Standard for SystemVerilog Chapter 22. Compiler directives
22.1 General 此子句描述以下编译器指令(按字母顺序列出): __FILE__ [22.13] __LINE__ [22.13] begin_keywords [22.14] celldefine [22.10] default_net…...
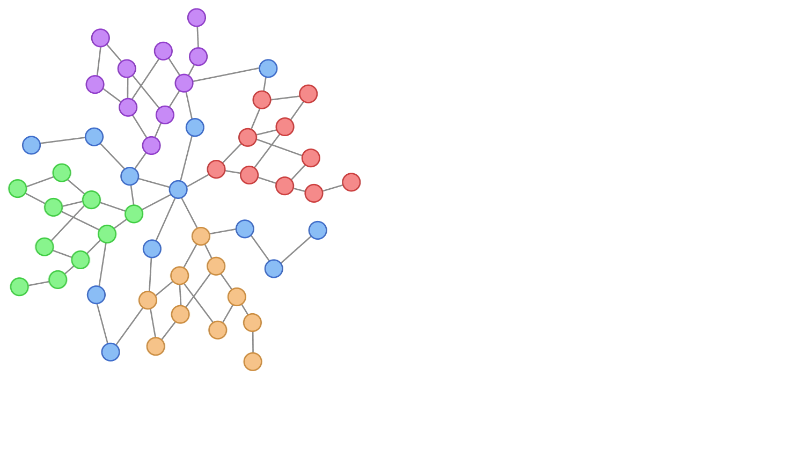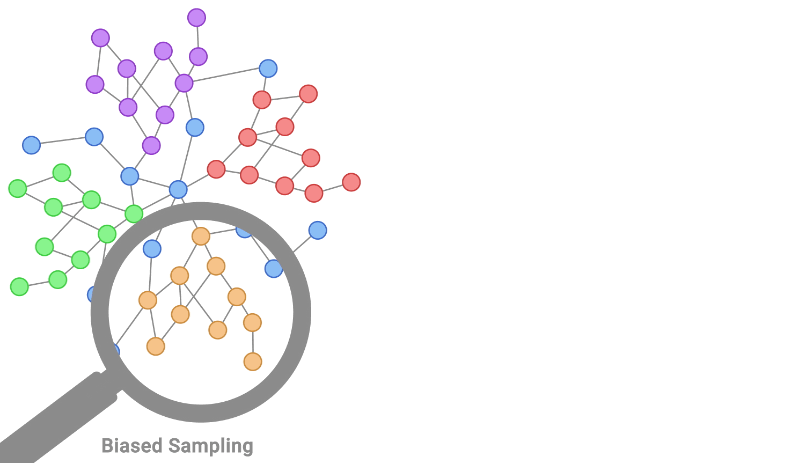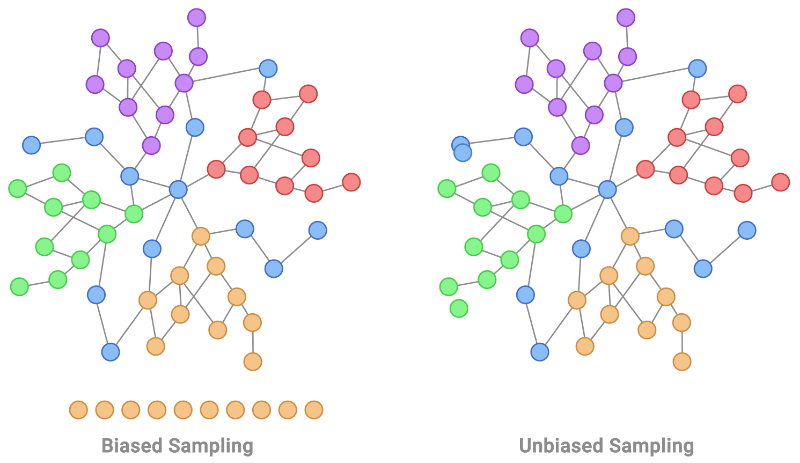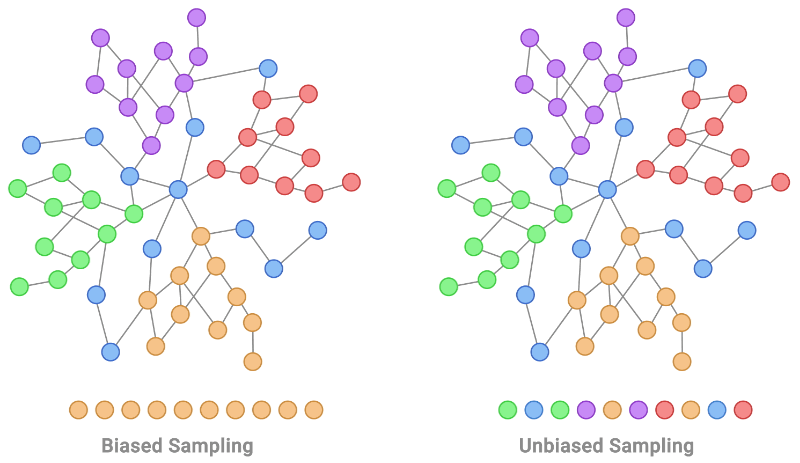
机器学习中的独立和同分布 (IID):假设和影响
一、介绍 在机器学习中,独立和同分布 (IID) 的概念在数据分析、模型训练和评估的各个方面都起着至关重要的作用。IID 假设是确保许多机器学习算法和统计技术的可靠性和有效性的基础。本文探讨了 IID 在机器学习中的重要性、其假设及其对模型开…...

PTP软硬件时间戳
软硬件时间戳 抄袭来源:http://www.bdtime.com.cn/pinlv/4296.html PTP 是一种网络协议,用于在计算机网络中进行时钟校准和时间同步。硬件时间戳和软件时间戳是在实现 PTP 时常见的两种方式,它们在精度、可靠性、实时性以及资源消耗等方面存…...
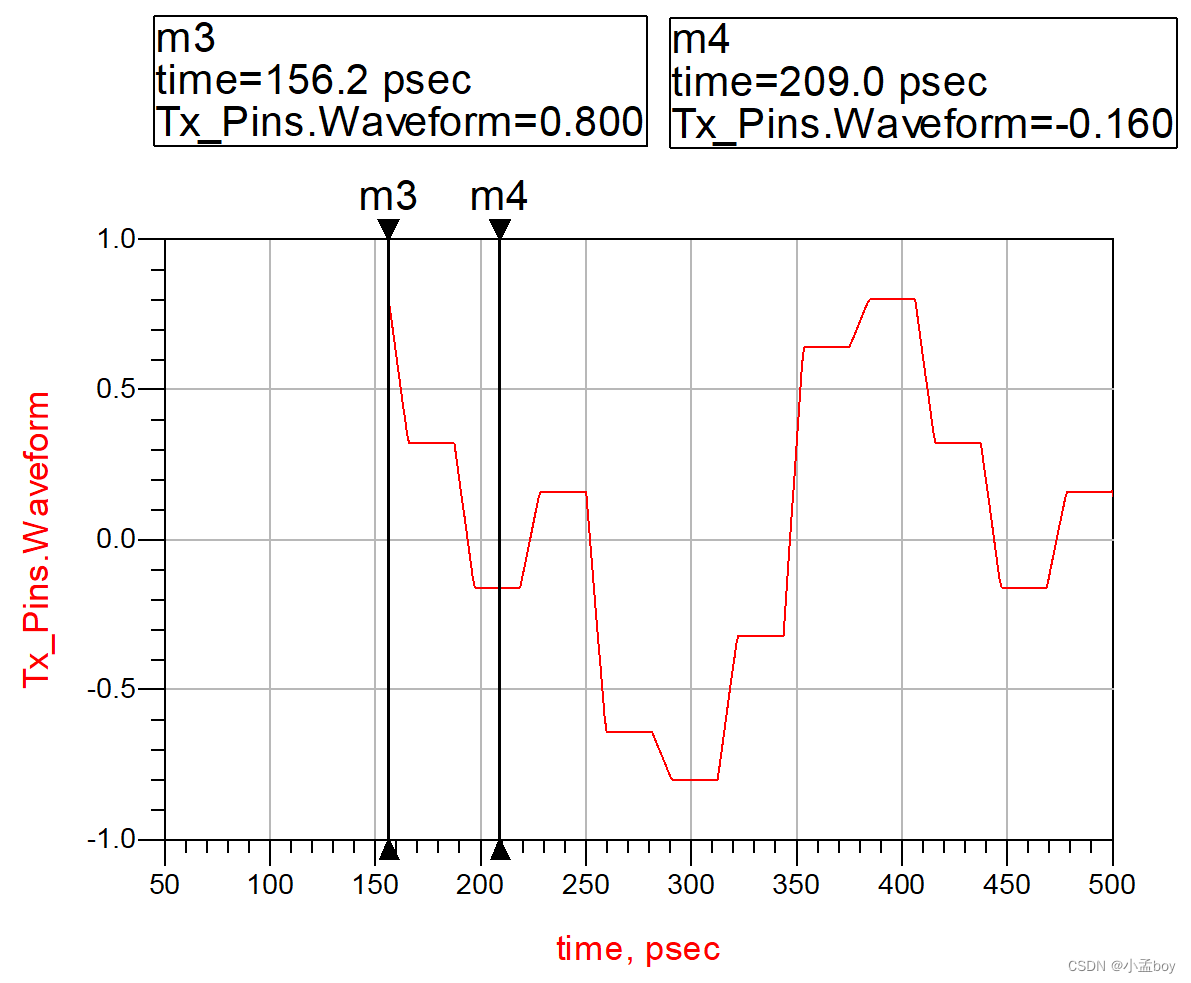
使用ADS进行serdes仿真时,Tx_Diff中EQ的设置对发送端波形的影响。
研究并记录一下ADS仿真中Tx_Diff的EQ设置。原理图如下: 最上面是选择均衡方法Choose equalization method:Specify FIR taps,Specify de-emphasis和none。 当选择Specify de-emphasis选项时,下方可以输入去加重具体的dB值&#x…...
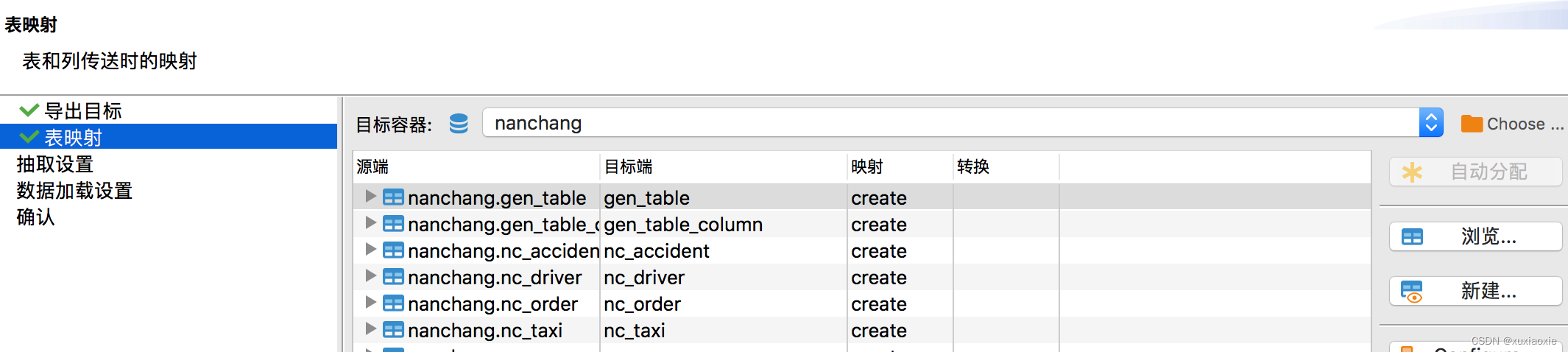
数据库迁移(DBeaver版本)
最近需要做一个数据库迁移, 测试环境开发的差不多了,需要将脚本迁移到生产。 中间了试了一些工具,比如Jetbrain出品的datagrip,这个数据库工具平时还是很好用的,但是数据迁移感觉不是那么好用,所以还是用到…...

【c++STL常见排序算法sort,merge,random_shuffle,reverse】
文章目录 C STL 常见排序算法详解1. sort 算法2. merge 算法3. random_shuffle 算法4. reverse 算法 C STL 常见排序算法详解 1. sort 算法 功能:sort 用于对容器内的元素进行升序排序。示例代码:#include <iostream> #include <algorithm>…...

STM32/N32G455国民科技芯片驱动DS1302时钟---笔记
这次来分享一下DS1302时钟IC,之前听说过这个IC,但是一直没搞过,用了半天时间就明白了原理和驱动,说明还是很简单的。 注:首先来区分一下DS1302和RTC时钟有什么不同,为什么不直接用RTC呢? RTC不…...
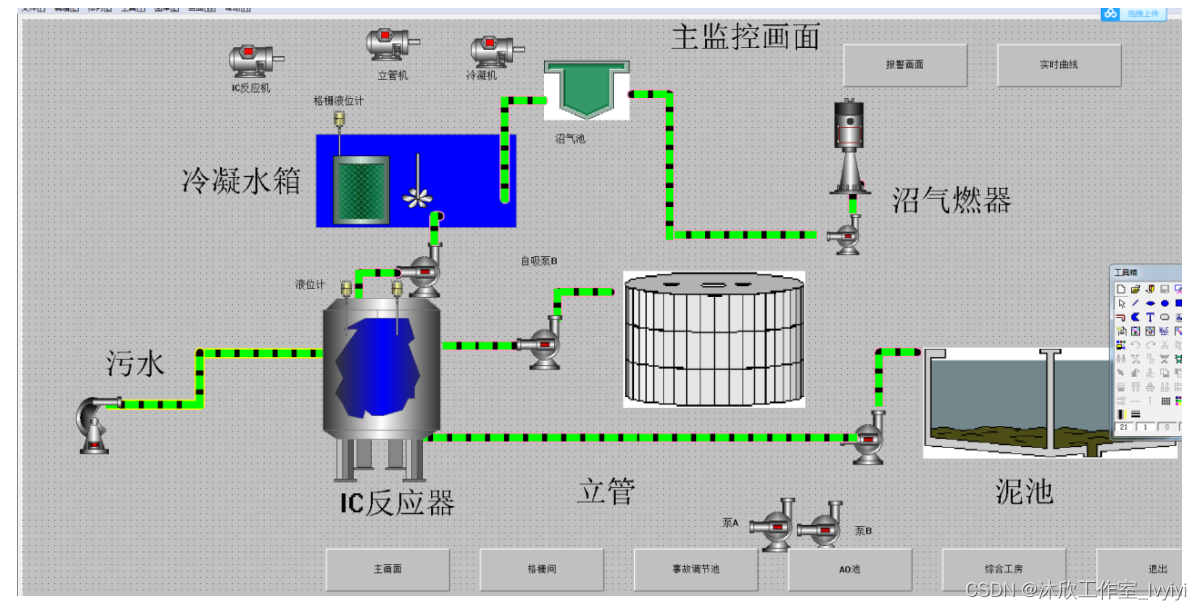
基于PLC的污水厌氧处理控制系统(论文+源码)
1. 系统设计 污水厌氧由进水系统通过粗格栅和清污机进行初步排除大块杂质物体以及漂浮物等,到达除砂池中。在除砂池系统中细格栅进一步净化污水厌氧中的细小颗粒物体,将污水厌氧中的细小沙粒滤除后进入氧化沟反应池。在该氧化沟系统中进行生化处理&…...
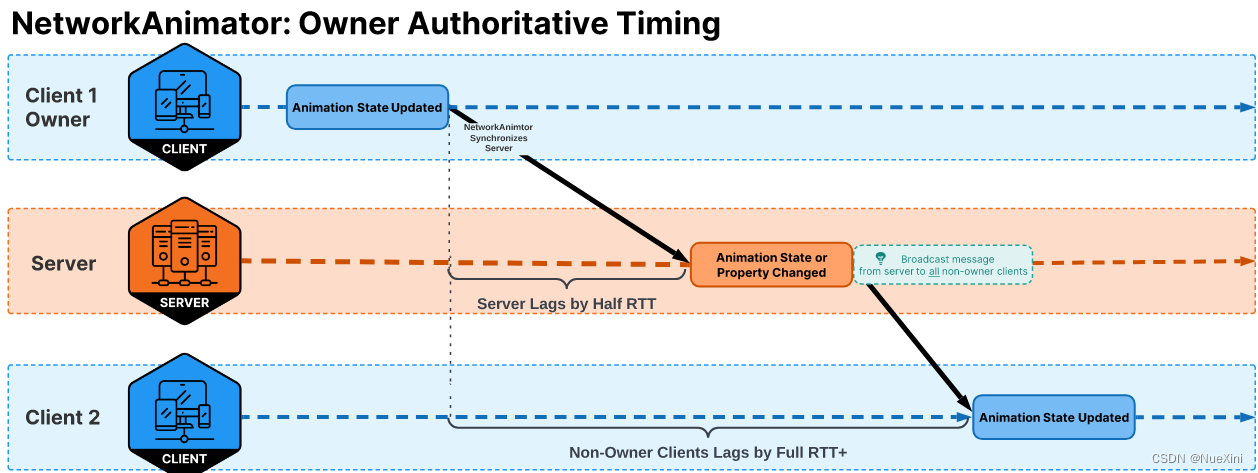
Unity之NetCode多人网络游戏联机对战教程(9)--NetworkAnimator组件
文章目录 前言NetworkAnimatorAnimator的Trigger属性服务器权威模式(Server Authoritative Mode)客户端权威模式 (Owner Authoritative Mode)学习文档 前言 这个组件是NetCode常用的组件之一,NetworkAnimator跟NetworkTransform一样…...

iceoryx之Roudi
目录...
常用转换byte转uint32、byte转float等)
.Net(C#)常用转换byte转uint32、byte转float等
1、byte转String Encoding.ASCII.GetString(byte[]); 2、base64string转byte byte[]Base64Decoder.Decoder.GetDecoded(string); 3、byte转UInt16 方法一 (UInt16)(bytes[0] * 256 bytes[1]) 方法二 (UInt16)((bytes[0] << 8) | bytes[1]); 方法三 字节序要对…...
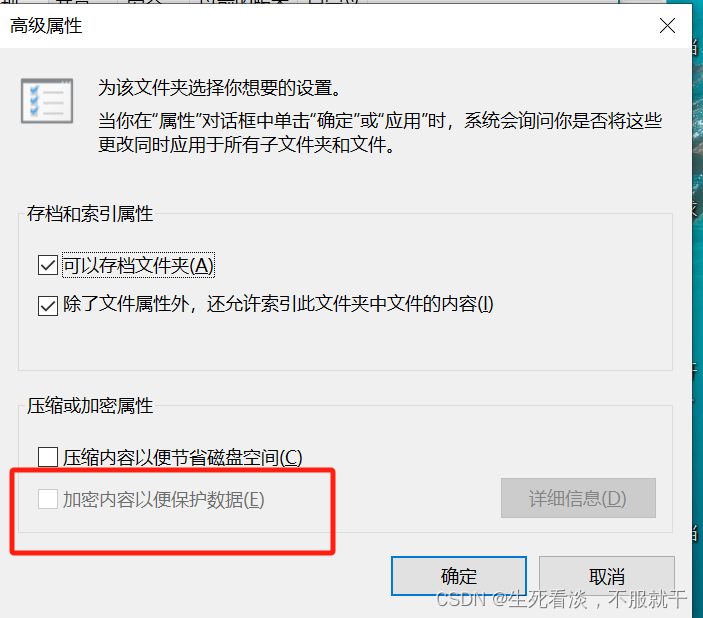
windows快捷方式图标变成空白
今天突然有客户说应用程序快捷方式图标变成了空白,就研究了一下,网上找了一下很多都说是什么图标缓存有问题,试过之后发现并不能解决问题。 然后发现用户的文件上都一把黄色的小锁的标志,查了一下说是文件属性里面设置加密之后就会…...
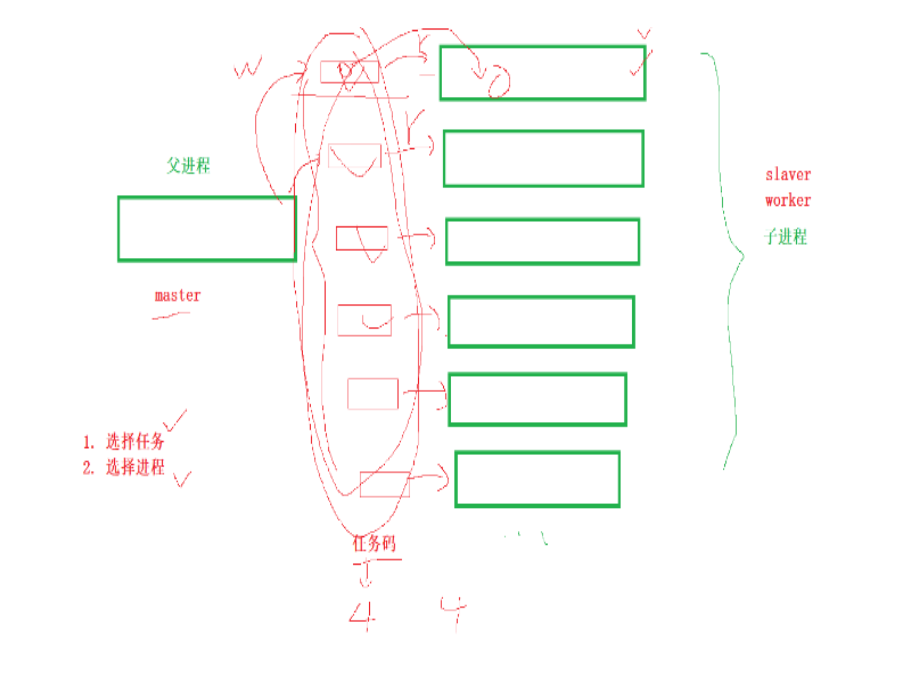
【Linux系统编程十九】:(进程通信)--匿名管道/模拟实现进程池
【Linux系统编程十九】:匿名管道原理/模拟实现进程池 一.进程通信理解二.通信实现原理三.系统接口四.五大特性与四种情况五.应用场景--进程池 一.进程通信理解 什么是通信? 通信其实就是一个进程想把数据给另一个进程,但因为进程具有独立性…...
【全网首发】2023年NOIP真题
目录 前言 真题 结尾 前言 NOIP题目了解一下,后续有可能会出讲解,题目全部来自于洛谷 真题 第一题:词典 第二题:三值逻辑 第三题:双序列扩展 第四题: 天天爱打卡 结尾 大家可以把你的预期分数打在评论…...
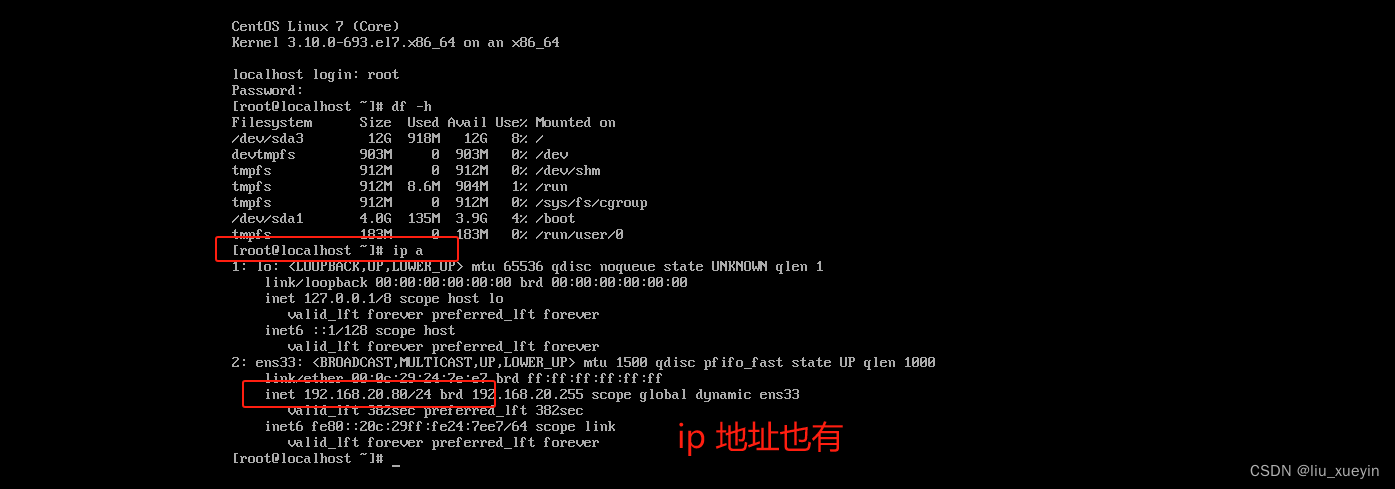
【Linux网络】从原理到实操,感受PXE无人值守自动化高效批量网络安装系统
一、PXE网络批量装机的介绍 1、常见的三种系统安装方式 2、回顾系统安装的过程,了解系统安装的必要条件 3、什么是pxe 4、搭建pxe的原理 5、Linux的光盘镜像中的isolinux中的相关文件学习 二、关于实现PXE无人值守装机的四大文件与五个软件的对应关系详解 5个…...

Pandas+Matplotlib 数据分析
利用可视化探索图表 一、数据可视化与探索图 数据可视化是指用图形或表格的方式来呈现数据。图表能够清楚地呈现数据性质, 以及数据间或属性间的关系,可以轻易地让人看图释义。用户通过探索图(Exploratory Graph)可以了解数据的…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
